Gujarat Board GSEB Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.2
(જો નું મૂલ્ય આપેલ ન હોય, તો π = \(\frac{22}{7}\))
પ્રશ્ન 1.
એક ઘન પદાર્થ એ 1 સેમી ત્રિજ્યા ધરાવતા અર્ધગોલક ઉપર તેટલી જ ત્રિજ્યાવાળો શંકુ ગોઠવીને બનાવાયો છે. શંકુની ઊંચાઈ એ તેની ત્રિજ્યા જેટલી છે, તો આ ઘન પદાર્થનું ઘનફળ ના ગુણિતમાં શોધો.
ઉત્તર:
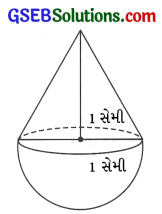
શંકુની તેમજ અર્ધગોલકની ત્રિજ્યા r = 1 સેમી
શંકુની ઊંચાઈ, h = શંકુની ત્રિજ્યા = 1 સેમી
ઘન પદાર્થનું ઘનફળ = શંકુનું ઘનફળ + અર્ધગોલકનું ઘનફળ
= \(\frac{1}{3}\) πr2h + \(\frac{2}{3}\) πr3
= (\(\frac{1}{3}\) π (1)2 (1) + \(\frac{2}{3}\) π (1)3) સેમી3
= π સેમી3
આમ, સંયોજિત ઘન પદાર્થનું ઘનફળ સેમી છે.

પ્રશ્ન 2.
એન્જિનિયરિંગના વિદ્યાર્થી રશેલને નળાકારના બંને છેડે પાતળી ઍલ્યુમિનિયમની શીટમાંથી બનેલો શંકુ બેસાડી એક નમૂનો તૈયાર કરવાનું કહેવામાં આવ્યું. નમૂનાનો વ્યાસ 3 સેમી અને લંબાઈ 12 સેમી છે. જો શંકુની ઊંચાઈ 2 સેમી હોય, તો રશેલે બનાવેલ નમૂનામાં કેટલી હવા સમાશે તે શોધો. (ધારી લો કે, નમૂનાના બહારના અને અંદરના માપો લગભગ સમાન છે.)
ઉત્તર:
બંને શંકુ તથા નળાકારની ત્રિજ્યા r = ![]() = \(\frac{3}{2}\) સેમી
= \(\frac{3}{2}\) સેમી
બંને શંકુની ઊંચાઈ h = 2 સેમી
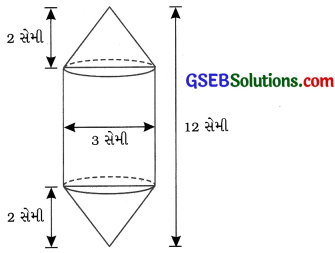
નળાકારની ઊંચાઈ, H = નમૂનાની કુલ ઊંચાઈ – 2 × શંકુની ઊંચાઈ
= (12 – 2 × 2) સેમી = 8 સેમી
નમૂનામાં સમાતી હવાનું ઘનફળ = નમૂનાનું ઘનફળ
= નળાકારનું ઘનફળ + 2 × શંકુનું ઘનફળ
= πr2H + 2 × \(\frac{1}{3}\) πr2 h સેમી
= πr2 (H + \(\frac{2}{3}\) h) સેમી
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2}\left(8+\frac{2}{3} \times 2\right)\) સેમી3
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times \frac{28}{3}\) સેમી3
= 66 સેમી3
આમ, નમૂનામાં 66 સેમીસેમી3 હવા સમાશે.

પ્રશ્ન 3.
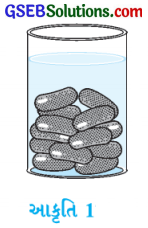
ગુલાબજાંબુમાં તેના કદના 30 % જેટલી ખાંડની ચાસણી છે. દરેક ગુલાબજાંબુનો આકાર નળાકારના બંને છેડે અર્ધગોલક લગાવ્યા હોય તેવો છે. તેની કુલ લંબાઈ 5 સેમી અને વ્યાસ 2.8 સેમી છે, તો આવા 45 ગુલાબજાંબુમાં આશરે કેટલી ખાંડની ચાસણી હશે તે શોધો. (જુઓ આકૃતિ 1)
ઉત્તર:
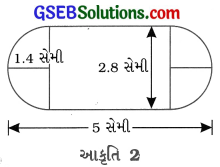
અહીં, નળાકાર ભાગની તેમજ બંને છેડે લાગેલ અર્ધગોલક ભાગોની ત્રિજ્યા r = ![]() = \(\frac{2.8}{2}\) સેમી = 1.4 સેમી
= \(\frac{2.8}{2}\) સેમી = 1.4 સેમી
નળાકાર ભાગની ઊંચાઈ (લંબાઈ), h = કુલ લંબાઈ – 2 × અર્ધગોલકોની ત્રિજ્યા
= (5 – 2 × 1.4) સેમી
= 2.2 સેમી
એક ગુલાબજાંબુનું ઘનફળ = નળાકાર ભાગનું ઘનફળ + 2 × અર્ધગોલક ભાગનું ઘનફળ
= πr2h + 2 × \(\frac{2}{3}\) πr3
= πr2 (h + \(\frac{4}{3}\) r)
= \(\frac{22}{7}\) × 1.4 × 1.4 (2.2 + \(\frac{4}{3}\) × 1.4) સેમી3
= 4.4 × 1.4 (\(\frac{6.6+5.6}{3}\)) સેમી3
= \(\frac{4.4 \times 1.4 \times 12.2}{3}\) સેમી3
45 ગુલાબજાંબુનું ઘનફળ = (45 × \(\frac{4.4 \times 1.4 \times 12.2}{3}\)) સેમી3
= (15 × 4.4 × 1.4 × 12.2) સેમી3
ચાસણીનું ઘનફળ = ગુલાબજાંબુના ઘનફળના 30 %
= \(\frac{30}{100}\) × 15 × 4.4 × 1.4 × 12.2 સેમી3
= 338.184 સેમી3
= 338 સેમી3 (આશરે)
આમ, 45 ગુલાબજાંબુમાં આશરે 338 સેમી3 ચાસણી હશે.

પ્રશ્ન 4.
એક લાકડાનું લંબઘન પેન-સ્ટૅન્ડ ચાર શંકુ આકારના છિદ્રવાળું બનાવેલું છે. લંબઘનનાં માપ 15 સેમી × 10 સેમી × 3.5 સેમી છે. છિદ્રવાળા દરેક ભાગની ત્રિજ્યા 0.5 સેમી અને ઊંડાઈ છે 1.4 સેમી છે, તો લાકડાના આ સ્ટેન્ડનું ઘનફળ શોધો. (જુઓ આકૃતિ)
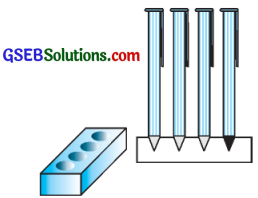
ઉત્તર:
લંબધન માટે, લંબાઈ =15 સેમી પહોળાઈ b = 10 સેમી અને ઊંચાઈ h = 3.5 સેમી
લંબઘનનું ઘનફળ = lbh
= (15 × 10 × 3.5) સેમી3 = 525 સેમી3
શંકુ આકારના ચાર છિદ્ર પૈકી દરેક છિદ્ર માટે, ત્રિજ્યા r = 0.5 સેમી અને ઊંચાઈ (ઊંડાઈ) h = 1.4 સેમી
શંકુ આકારના ચાર છિદ્રનું ઘનફળ = 4 × \(\frac{1}{3}\) πr2h
= 4 × \(\frac{1}{3}\) × \(\frac{22}{7}\) × 0.5 × 0.5 × 1.4 સેમી3
= 4 × \(\frac{1}{3} \times \frac{22}{7} \times \frac{1}{2} \times \frac{1}{2} \times \frac{14}{10}\) સેમી3
= \(\frac{22}{15}\) સેમી3.
= 1.47 સેમી3
લાકડાના સ્ટેન્ડનું ઘનફળ = લંબઘનનું ઘનફળ – શંકુ આકારના ચાર છિદ્રનું ઘનફળ
= (525 – 1.47) સેમી = 523.53 સેમી3
આમ, લાકડાના સ્ટેન્ડનું ઘનફળ 523.53 સેમી3 છે.

પ્રશ્ન 5.
એક વાસણનું સ્વરૂપ ઊંધા શંકુ જેવું છે. તેની ઊંચાઈ 8 સેમી અને ઉપરના ભાગની ત્રિજ્યા 5 સેમી છે. તે ઉપરની ધાર સુધી પાણીથી ભરેલું છે. જ્યારે વાસણમાં 0.5 સેમી ત્રિજ્યાવાળી ધાતુની ગોળીઓ નાખવામાં આવે છે, ત્યારે એક-ચતુર્ભાશ જેટલું પાણી બહાર નીકળે છે, તો વાસણમાં નાખેલી ધાતુની ગોળીઓની સંખ્યા શોધો.
ઉત્તર:
શંકુ આકારના વાસણ માટે, ત્રિજ્યા r = 5 સેમી અને ઊંચાઈ h = 8 સેમી
સંપૂર્ણ રીતે ભરેલા વાસણમાંના પાણીનું ઘનફળ = શંકુનું ઘનફળ
= \(\frac{1}{3}\) πr2h
= \(\frac{1}{3}\) × π × 5 × 5 × 8 સેમી3
= \(\frac{200}{3}\) π સેમી3
હવે, પાણીમાં ધાતુની ગોળીઓ નાખતાં એક-ચતુર્થાંશ જેટલું છે પાણી બહાર નીકળે છે.
વહી જતા પાણીનું ઘનફળ = \(\frac{1}{4}\) × \(\frac{200}{3}\) π સેમી3
= \(\frac{50}{3}\) π સેમી3
ધારો કે, પાણીમાં n ગોળીઓ નાખવામાં આવે છે, જે દરેક રે ગોળી માટે ત્રિજ્યા r = 0.5 સેમી = \(\frac{1}{2}\) સેમી
આથી ધાતુની n ગોળીઓનું ઘનફળ = વહી જતા પાણીનું ઘનફળ
∴ n × \(\frac{4}{3}\) π r3 = \(\frac{50}{3}\) π
∴ n × \(\frac{4}{3} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\) = \(\frac{50}{3}\)
∴ n = 100
આમ, વાસણમાં નાખેલ ધાતુની ગોળીઓની સંખ્યા 100 છે.

પ્રશ્ન 6.
એક લોખંડના નળાકાર સ્વરૂપના નક્કર થાંભલાની ઊંચાઈ 220 સેમી છે અને પાયાનો વ્યાસ 24 સેમી છે. તેની ઉપર 60 સેમી ઊંચાઈ અને 8 સેમી ત્રિજ્યાવાળા બીજા નળાકારને મૂકવામાં આવે છે, તો થાંભલાનું દળ શોધો. 1 સેમી3 લોખંડનું દળ આશરે 8 ગ્રામ છે. (π = 3.14 લો.)
ઉત્તર:
નીચેના નળાકાર માટે, ત્રિજ્યા r1 = ![]() = \(\frac{24}{2}\) સેમી = 12 સેમી
= \(\frac{24}{2}\) સેમી = 12 સેમી
અને ઊંચાઈ h1 = 220 સેમી
ઉપરના નળાકાર માટે, ત્રિજ્યા r2 = 8 સેમી અને ઊંચાઈ h2 = 60 સેમી
થાંભલાનું ઘનફળ = નીચેના નળાકારનું ઘનફળ + ઉપરના નળાકારનું ઘનફળ
= πr12 h1 + π r22 h2
= π (r12 h1 + r22 h2)
= 3.14 (12 × 12 × 220 + 8 × 8 × 60) સેમી3
= 3.14 × 35520 સેમી3
1 સેમી લોખંડનું દળ = 8 ગ્રામ = 0.008 કિગ્રા
∴ 3.14 × 35520 સેમી3 લોખંડનું દળ
= 3.14 × 35520 × 0.008 કિગ્રા
= 892.2624 કિગ્રા
= 892.26 કિગ્રા (આશરે)
આમ, થાંભલાનું દળ 892.26 કિગ્રા (આશરે) છે.

પ્રશ્ન 7.
60 સેમી ત્રિજ્યાવાળા અર્ધગોલક પર સ્થિત લંબવૃત્તીય શંકુની ઊંચાઈ 120 સેમી અને ત્રિજ્યા 60 સેમી છે. તેને પાણીથી સંપૂર્ણ ભરેલા એક લંબવૃત્તીય નળાકારમાં તેના તળિયાને સ્પર્શ તે રીતે ઊભો મૂક્યો છે. જો નળાકારની ત્રિજ્યા 60 સેમી અને ઊંચાઈ 180 સેમી હોય, તો નળાકારમાં બાકી રહેલા પાણીનું ઘનફળ શોધો.
ઉત્તર:
સંયોજિત ઘન પદાર્થ માટે, શંકુની ત્રિજ્યા = અર્ધગોલકની ત્રિજ્યા = r = 60 સેમી અને શંકુની ઊંચાઈ = h = 120 સેમી
સંયોજિત ઘન પદાર્થનું ઘનફળ = શંકુનું ઘનફળ + અર્ધગોલકનું ઘનફળ
= \(\frac{1}{3}\) πr2 h + \(\frac{2}{3}\) πr3
= \(\frac{1}{3}\) πr2 (h + 2r)
= \(\frac{1}{3}\) × π × 60 × 60 (120 + 2 × 60) સેમી3
= \(\frac{1}{3}\) × π × 60 × 60 × 240 સેમી3
= π × 60 × 60 × 80 સેમી3
નળાકાર પાત્ર માટે, ત્રિજ્યા R = 60 સેમી અને ઊંચાઈ H = 180 સેમી
નળાકાર પાત્રમાં શરૂઆતમાં રહેલ પાણીનું ઘનફળ = નળાકારનું ઘનફળ
= πR2H
= π × 60 × 60 × 180 સેમી3
સંયોજિત ઘન પદાર્થને નળાકારમાં મૂક્યા બાદ નળાકારમાં બાકી રહેલા પાણીનું ઘનફળ = નળાકારનું ઘનફળ – સંયોજિત ઘન પદાર્થનું ઘનફળ
= [(π × 60 × 60 × 180) – (π × 60 × 60 × 80)] સેમી3
= π × 60 × 60 (180 – 80) સેમી3
= π × 60 × 60 × 100 સેમી3
= \(\frac{22 \times 60 \times 60 \times 100}{7 \times 1000000}\) મી3 (1 મી3 = 1000000 સેમી)
= 1.131 મી3 (આશરે)
આમ, નળાકારમાં બાકી રહેલા પાણીનું ઘનફળ 1.131 મી3 (આશરે) છે.

પ્રશ્ન 8.
એક ગોળાકાર કાચના વાસણની ઉપરનો ભાગ નળાકાર છે. તે નળાકારની ઊંચાઈ 8 સેમી છે અને વ્યાસ 2 સેમી છે. ગોળાકાર ભાગનો વ્યાસ 8.5 સેમી છે. એક બાળક માહિતી પ્રાપ્ત કરે છે કે તેમાં ભરેલા પાણીનું ઘનફળ 345 સેમી3 છે. બાળકનો જવાબ સાચો છે કે નહિ તે ચકાસો. ઉપરનાં માપો તેના અંદરના ભાગના છે. π = 3.14 લો.
ઉત્તર:
વાસણના નળાકાર ભાગ માટે,
ત્રિજ્યા r = ![]() = \(\frac{2}{2}\) = 1 સેમી અને ઊંચાઈ h = 8 સેમી
= \(\frac{2}{2}\) = 1 સેમી અને ઊંચાઈ h = 8 સેમી
વાસણના ગોળાકાર ભાગ માટે,
ત્રિજ્યા R = ![]() = \(\frac{8.5}{2}\)સેમી = 4.25 સેમી = \(\frac{17}{4}\) સેમી
= \(\frac{8.5}{2}\)સેમી = 4.25 સેમી = \(\frac{17}{4}\) સેમી
કાચના વાસણનું ઘનફળ = નળાકાર ભાગનું ઘનફળ + ગોળાકાર ભાગનું ઘનફળ
= πr2h + \(\frac{4}{3}\) πR3
= π (r2h + \(\frac{4}{3}\) R3)
= 3.14 (1 × 1 × 8 + \(\frac{4}{3} \times \frac{17}{4} \times \frac{17}{4} \times \frac{17}{4}\)) સેમી3
= 3.14 (110.354) સેમી3 (આશરે)
= 346.51 સેમી3
(આશરે) બાળકનો જવાબ સાચો નથી, કારણ કે તેની માહિતી મુજબ વાસણનું ઘનફળ 345 સેમી3 છે, જ્યારે સાચું ઘનફળ 346.51 સેમી3 (આશરે) છે.