Gujarat Board GSEB Solutions Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4
Question 1.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Here
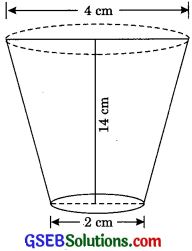
d1 = 4 cm
r1 = \(\frac {4}{2}\) = 2 cm
and d2 = 2 cm
r2 = 1 cm
Height h = 14
Hence, capacity of glass
= \(\frac {1}{3}\) π (r21 + r21 + r1r2) x h
= \(\frac {1}{3}\) x \(\frac {22}{7}\) [22 + 12 + 2 x 1] x 14
= \(\frac {1}{3}\) x \(\frac {22}{7}\) x [4 + 1 + 2] x 14
= \(\frac {22}{3 x 7}\) x 7 x 14 = \(\frac {308}{3}\) cm3 = 102 \(\frac {2}{3}\) cm2
![]()
Question 2.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:
Here,
Slant height l = 4 cm
and let r1 r2 be the radii of frustum and r1 > r2
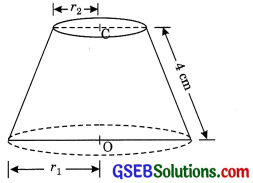
Perimeter of circular ends = 2πr1
2πr1 = 18 cm
⇒ πr1 = 9 cm ……(1)
and 2πr2 = 6 cm
πr2 = 3 cm …….(2)
Curved surface area of frustum
= π(r1 + r2) l = (πr1 + πr2)l ……(3)
Putting value of eqn. (1) and (2) in eqn. (3),
Curved surface area of frustum = (9 + 3) x 4 = 12 x 4 = 48 cm2
Question 3.
A fez, the cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Solution:
Here
r1 = 10 cm (Radius on the open side)
and r1 = 4 cm (Radius of the upper base)
Surface area of cap = CSA of frustum + Area of upper circular end
= π(r1 + r2) l + πr22

Question 4.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹8 per 100 cm2. (Take π = 3.14)
Solution:
Here
h = 16 cm
r1 = 20 cm and r2 = 8 cm
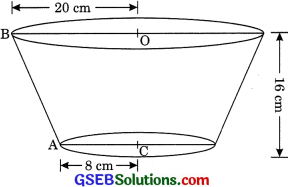
Volume of frustum shaped container
= \(\frac {1}{3}\)πh (r21 + r22 + r12)
= \(\frac {1}{3}\) x 3.14 x 16(202 + 82 + 20 x 8)nh
= \(\frac {1}{3}\) x 3.14 x 16 [400 + 64 + 160]
= \(\frac {1}{3}\) x 3.14 x 16 x 624
= 3.14 x 16 x 208
= 10449.92 cm3 (1000 cm3 = 1 litre)
= \(\frac{10449.92}{1000}\) = 10.44992 litre
Cost of milk = 10.44992 x 20
= ₹ 208.9984 = ₹ 209
Surface area of frustum
= π (r1 + r2)l + πr22 ……….(1)
l = \(\frac{10449.92}{1000}\)
= \(\sqrt{\left(r_{1}-r_{2}\right)^{2}+h^{2}}\)
= \(\sqrt{(20-8)^{2}+16^{2}}\)
= \(\sqrt{12^{2}+16^{2}}\)
= \(\sqrt{144+256}\)
= \(\sqrt{400}\)
l = 20 cm
Area of metal sheet = Surface area of frustum
= π(r1 + r2)l + πr22 [From (1)]
= 3.14 (20 + 8) x 20 + 3.14 x 82
= 3.14 x 28 x 20 + 3.14 x 64
= 1758.4 + 200.96
= 1959.36 cm2
Cost of metal sheet
= 1959.36 x \(\frac{8}{100}\) = ? 156.75
![]()
Question 5.
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \(\frac{1}{16}\) cm, find the length of the wire.
Solution:
Here height h of cone = 20 cm
Cone is cut into the middle then height of frustum
= \(\frac{20}{2}\) = 20 cm
Hence AC = 10 cm
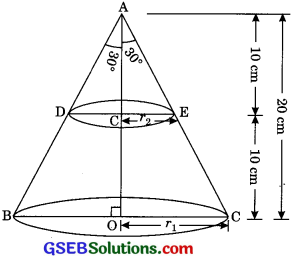
In rt. ΔACE
tan 300 = \(\frac{CE}{AC}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{r_{2}}{10}\)
⇒ r2 = \(\frac{10}{\sqrt{3}}\) cm
Now rt. ΔAOB
tan 300 = \(\frac{OC}{OA}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{r_{1}}{20}\)
⇒ r1 = \(\frac{20}{\sqrt{3}}\) cm
Volume of frustum

Diameter of wire which is drawn = \(\frac{1}{16}\)cm
Radius of wire r = \(\frac{1}{2}\) x \(\frac{1}{16}\) = \(\frac{1}{32}\)cm
Volume of wire drawn = Volume of frustum
πr2h = \(\frac{22000}{9}\)

= 7964.4 m
Hence, the length of wire is 7964.4 in.
![]()