GSEB Solutions Class 10 Maths Chapter 14 આંકડાશાસ્ત્ર Ex 14.1

Gujarat Board GSEB Solutions Class 10 Maths Chapter 14 આંકડાશાસ્ત્ર Ex 14.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 14 આંકડાશાસ્ત્ર Ex 14.1

પ્રશ્ન 1.
વિદ્યાર્થીઓના એક સમૂહ દ્વારા તેમના પર્યાવરણ જાગૃતિ કાર્યક્રમના ભાગરૂપે એક સર્વેક્ષણ હાથ ધરવામાં આવ્યું. તેમાં તેમણે એક વિસ્તારના 20 ઘરોમાં વનસ્પતિના છોડની સંખ્યા વિશે નીચેની માહિતી એકઠી કરી. ઘરદીઠ છોડની સંખ્યાઓનો મધ્યક શોધો.

મધ્યક શોધવા માટે કઈ રીતનો ઉપયોગ કરશો અને શા માટે?
ઉત્તર:
અહીં, f_i તેમજ x_i ની કિંમતો નાની હોવાથી મધ્યક શોધવા સીધી રીતનો ઉપયોગ કરીશું. છોડની સંખ્યા (વર્ગ)

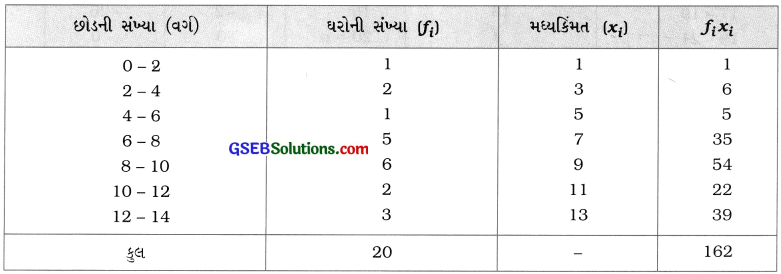
હવે, મધ્યક \(\bar{x}=\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}=\frac{162}{20}\) = 81
આમ, ઘરદીઠ છોડની સંખ્યાઓનો મધ્યક 8.1 છે.

પ્રશ્ન 2.
એક ફેક્ટરીમાં 50 કારીગરોના દૈનિક વેતનના નીચે આપેલ વિતરણનો વિચાર કરો:

યોગ્ય રીતનો ઉપયોગ કરીને કારખાનાના કારીગરોના દૈનિક વેતનનો મધ્યક શોધો.
ઉત્તર:
અહીં, પદ-વિચલનની રીત યોગ્ય રહેશે. a = 550 અને h = 20 લઈ નીચેનું કોષ્ટક રચીએ:

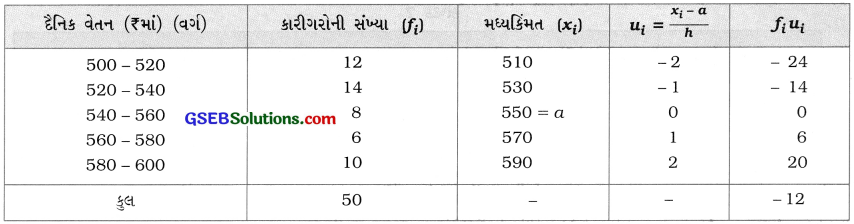
હવે, મધ્યક \(\bar{x}=a+\frac{2 f_{i} u_{i}}{\Sigma f_{i}} \times h\)
= 550 + \(-\frac{12}{50}\) × 20
= 550 – 4.80
= 545.20
આમ, કારખાનાના કારીગરોના દૈનિક વેતનનો મધ્યક ₹ 545.20 છે.

પ્રશ્ન 3.
નીચેનું આવૃત્તિ-વિતરણ વસતીનાં બાળકોનું દૈનિક ખિસ્સાભથું દર્શાવે છે. ખિસ્સાભથ્થાનો મધ્યક ₹ 18 છે. ખૂટતી આવૃત્તિ f શોધો.

ઉત્તર:
અહીં, આપણે ધારી લીધેલ મધ્યકની રીતે વાપરવા a = 20 લઈને નીચેનું કોષ્ટક બનાવીએ :

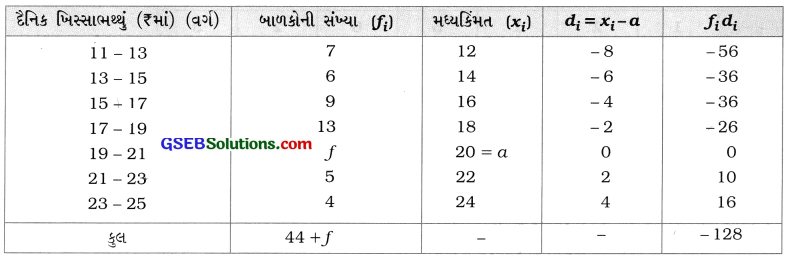
સૂત્રમાં કિંમતો મૂકતાં,
મધ્ય, \(\bar{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)

∴ 18 = 20 + \(\frac{-128}{44+f}\)
∴ – 2 = – \(\frac{128}{44+f}\)
∴ 44 + f = 64
∴ f = 20
આમ, ખૂટતી આવૃત્તિ f = 20 છે.

પ્રશ્ન 4.
એક હૉસ્પિટલમાં દાક્તરે ત્રીસ મહિલાઓની શારીરિક તપાસ અને પ્રતિમિનિટ હૃદયના ધબકારાની નોંધ કરી તથા નીચે પ્રમાણે સારાંશ તૈયાર કર્યો. યોગ્ય રીતે પસંદ કરીને, આ મહિલાઓના પ્રતિમિનિટ હૃદયના ધબકારાનો મધ્યક શોધો.

ઉત્તર:
અહીં, ની કિંમતો નાની હોવાથી a = 75.5 લઈને ધારી લીધેલ મધ્યકની રીત વાપરવા નીચેનું કોષ્ટક બનાવીએ:

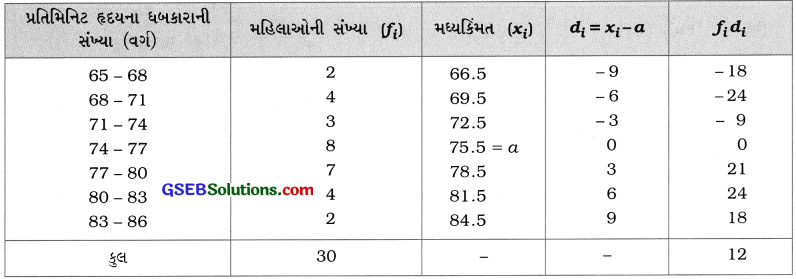
સૂત્રમાં કિંમતો મૂકતાં,
મધ્યક \(\bar{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)
= 75.5 + \(\frac{12}{30}\)
= 75.9
આમ, તપાસ કરેલ મહિલાઓના પ્રતિમિનિટ હૃદયના ધબકારાનો મધ્યક 75.9 છે.

પ્રશ્ન 5.
એક છૂટક વેચાણ બજારમાં, ફળ વેચનારાઓ બંધ ખોખાંઓમાં કેરીઓ વેચી રહ્યા હતા. આ ખોખાંઓમાં કેરીઓ જુદી જુદી સંખ્યામાં હતી. ખોખાંઓની સંખ્યાનાં પ્રમાણ કેરીઓનું આવૃત્તિ-વિતરણ નીચે પ્રમાણે હતું:

બંધ ખોખાંમાં મૂકેલ કેરીઓની સંખ્યાનો મધ્યક શોધો. મધ્યક શોધવા માટે તમે કઈ રીતે પસંદ કરી હતી?
ઉત્તર:
અહીં, આપણે પદ-વિચલનની રીતનો ઉપયોગ કરીએ. a = 57 અને h = 3 લઈને નીચેનું કોષ્ટક રચીએ:

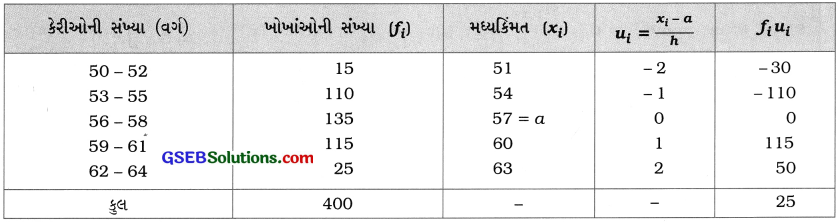
સૂત્રમાં કિંમતો મૂકતાં,
મધ્યક, \(\bar{x}=a+\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}} \times h\)
= 57 + \(\frac{25}{400}\) × 3
= 57 + 0.1875 = 57.1875 = 57.19 (આશરે)
આમ, બંધ ખોખાંમાં મૂકેલ કેરીઓની સંખ્યાનો મધ્યક 17.19 છે.

પ્રશ્ન 6.
નીચેનું કોષ્ટક એક વિસ્તારમાં 25 પરિવારના ખોરાકનો દૈનિક ઘરગથ્થુ ખર્ચ બતાવે છે :

પરિવારના ખોરાક પરના દૈનિક ઘરગથ્થુ ખર્ચનો મધ્યક યોગ્ય રીતનો ઉપયોગ કરીને શોધો.
ઉત્તર:
અહીં, પદ-વિચલનની રીતનો ઉપયોગ કરવા a = 225 અને h = 50 લઈને નીચેનું કોષ્ટક રચીએ :

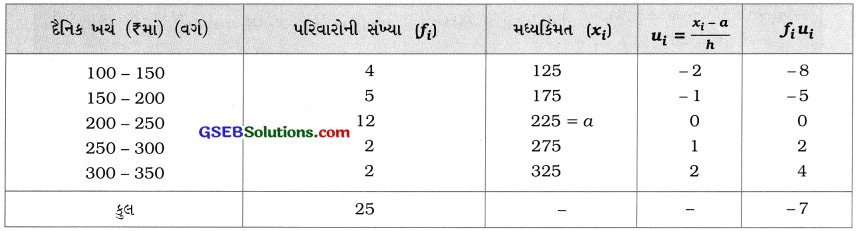
સૂત્રમાં કિંમતો મૂકતાં,
મધ્યક, \(\bar{x}=a+\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}} \times h\)
= 225 + \(-\frac{7}{25}\) × 50
= 225 – 14 = 211
આમ, પરિવારના ખોરાક પરના દૈનિક ઘરગથ્થુ ખર્ચનો મધ્યક ₹ 211 છે.

પ્રશ્ન 7.
એક ચોક્કસ શહેરમાં 30 વિસ્તારોમાં હવામાં SO₂ ની સાંદ્રતા (ઘટકો પ્રતિ દસ લાખમાં, એટલે કે ppmમાં) શોધવા માટે નીચે દર્શાવેલ માહિતી એકત્રિત કરવામાં આવી હતી:

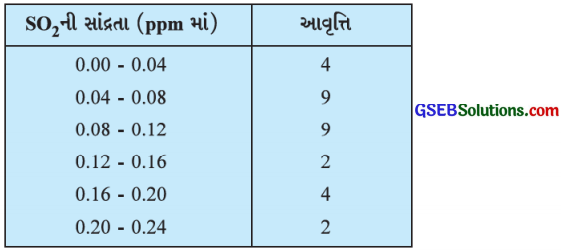
હવામાં SO₂ ની સાંદ્રતાનો મધ્યક શોધો.
ઉત્તર:
અહીં, h = 0.04 છે. પદ-વિચલનની રીતનો ઉપયોગ કરવા a = 0.10 લઈને નીચેનું કોષ્ટક રચીએ :

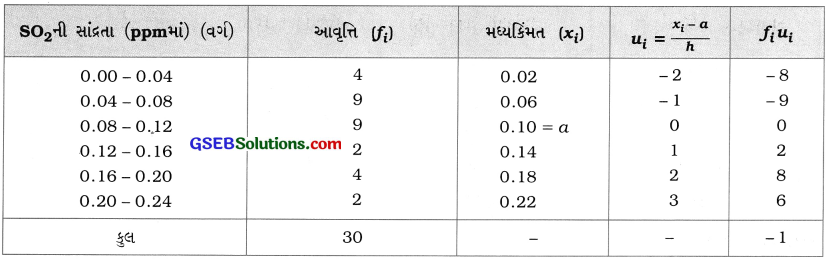
સૂત્રમાં કિંમતો મૂકતાં,
મધ્યક, \(\bar{x}=a+\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}} \times h\)
= 0.10 + \(-\frac{1}{30}\) × 0.04
= 0.10 – 0.001 = 0.099
આમ, હવામાં SO₂ ની સાંદ્રતાનો મધ્યક 0.09 (ppm માં) છે.

પ્રશ્ન 8.
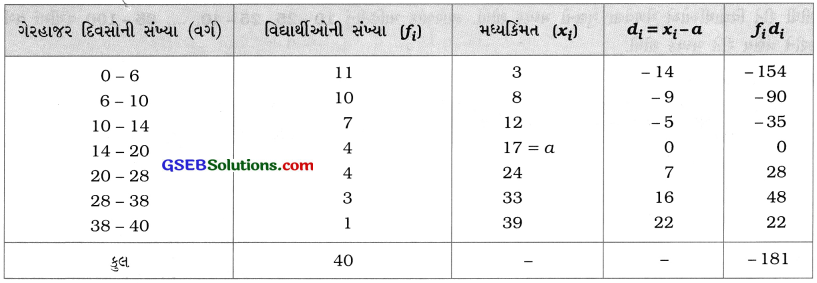
એક વર્ગના સમગ્ર સત્રની 40 વિદ્યાર્થીઓની ગેરહાજરીની યાદી વર્ગશિક્ષક પાસે છે. વિદ્યાર્થીઓની ગેરહાજર દિવસોની સંખ્યાનો મધ્યક શોધો.

ઉત્તર:
અહીં, ધારી લીધેલ મધ્યકની રીતનો ઉપયોગ કરવા a = 17 લઈને નીચેનું કોષ્ટક રચીએ :

સૂત્રમાં કિંમતો મૂકતાં,
મધ્યક \(\bar{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)

= 17 + \(-\frac{181}{40}\)

= 17 – 4.525 = 12.475 = 12.48 (આશરે)
આમ, વિદ્યાર્થીઓની ગેરહાજર દિવસોની સંખ્યાનો મધ્યક 12.48 દિવસ છે.

પ્રશ્ન 9.
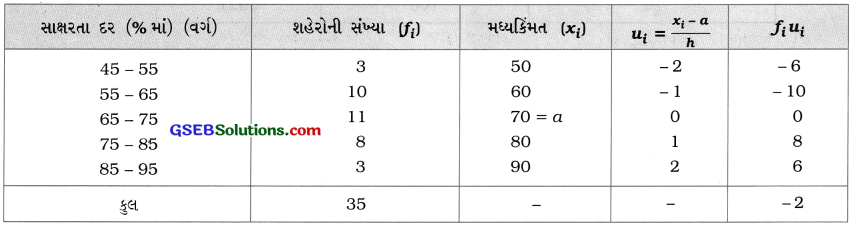
નીચેનું કોષ્ટક 35 શહેરોમાં સાક્ષરતા દર (પ્રતિશતમાં) આપે છે. સાક્ષરતા દરનો મધ્યક શોધો.

ઉત્તર:
અહીં, h = 10 છે. પદ-વિચલનની રીતનો ઉપયોગ કરવા a = 70 લઈને નીચેનું કોષ્ટક બનાવીએ :

સૂત્રમાં કિંમતો મૂકતાં,
મધ્યક \(\bar{x}=a+\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}} \times h\)
= 70 + \(-\frac{2}{35}\) × 10
= 70 – 0.57 = 69.43
આમ, આપેલ શહેરોમાં સાક્ષરતા દરનો મધ્યક 69.43 % છે.