Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.1
પ્રશ્ન 1.
આફતાબ તેની દીકરીને કહે છે, “સાત વર્ષ પહેલાં મારી ઉંમર તે વખતની તારી ઉંમર કરતાં સાત ગણી હતી. હવે પછીના ત્રણ વર્ષ પછી મારી ઉંમર તારી તે વખતની ઉંમર કરતાં ત્રણ ગણી હશે.” (શું આ રસપ્રદ છે?) આ પરિસ્થિતિને બૈજિક રીતે અને આલેખની રીતે દર્શાવો.
ઉત્તરઃ
ધારો કે, આફતાબની હાલની ઉંમર ૪ વર્ષ અને તેની દીકરીની હાલની ઉંમર ૫ વર્ષ છે, તો સાત વર્ષ પહેલાં આફતાબની ઉંમર x – 7 વર્ષ અને તેની દીકરીની ઉંમર y – 7 વર્ષ હતી. આથી આપેલ માહિતી મુજબ,
x – 7 = 7 (y – 7)
∴ x – 7 = 7y -49.
∴ x – 7y + 42 = 0 ……….. (1)
તે જ રીતે, ત્રણ વર્ષ બાદ આફતાબની ઉંમર x + 3 વર્ષ અને તેની દીકરીની ઉંમર પy+ 3 વર્ષ થશે. આથી આપેલ માહિતી મુજબ,
x + 3 = 3(y + 3)
∴ x + 3 = 3y + 9
∴ x – 3y – 6 = 0 …………… (2)
આમ, સમીકરણો x – 7y + 42 = 0 અને x – 3y – 6 = 0 એ આપેલ પરિસ્થિતિને બેજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને આલેખની રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.
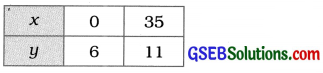
x – 7y + 42 = 0
∴ y = \(\frac{42+x}{7}\)
x – 3y – 6 = 0
∴ y = \(\frac{x-6}{3}\)
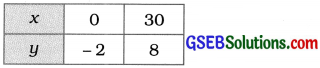
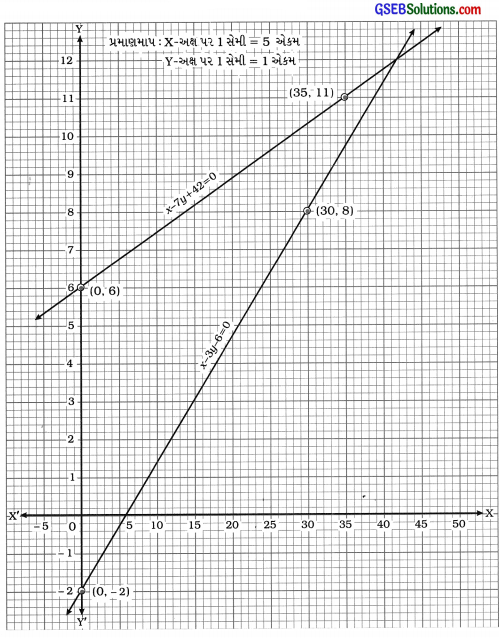
ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને આલેખની રીતે દર્શાવે છે. તમે જોઈ શકો છો કે, બંને રેખા બિંદુ (42, 12)માં છેદે છે.

પ્રશ્ન 2.
ક્રિકેટ-ટીમના પ્રશિક્ષક ૨ 3900માં ૩ બૅટ અને 6 દડા ખરીદે છે. પછી તે બીજું તે જ પ્રકારનું 1 બેટ અને તે જ. પ્રકારના વધુ 3 દડા ₹ 1300માં ખરીદે છે. આ પરિસ્થિતિને ઐજિક અને ભૌમિતિક રીતે દર્શાવો.
ઉત્તરઃ
ધારો કે, એક બૅટની કિંમત ₹ x અને એક દડાની કિંમત ₹ y છે. આથી 3 બૅટની કુલ કિંમત ₹ 3x અને 6 દડાની કુલ કિંમત ₹ 6y થાય. આપેલ માહિતી મુજબ 3 બૅટ અને 6 દડાની કુલ કિંમત ₹ 3900 છે.
∴ 3x + 6y = 3900
∴ x + 2y = 1300
તે જ રીતે, 1 બૅટની કિંમત ₹ x અને 3 દડાની કુલ કિંમત ₹ 3y 3પ થાય. આપેલ માહિતી મુજબ 1 બૅટ અને 3 દડાની કુલ કિંમત ₹ 1300 છે.
∴ x + 3y = 1300
આમ, સમીકરણો x + 2y = 1800 અને x + 3y = 1300 આપેલ પરિસ્થિતિને બૈજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.
x + 2y = 1300

x + 3y = 1300

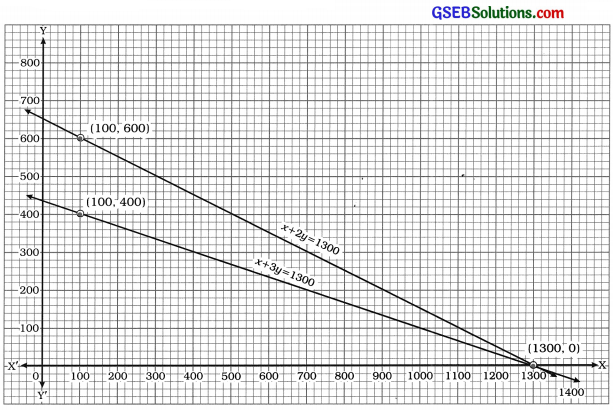
ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવે છે. તમે જોઈ શકો છો કે, બંને રેખા બિંદુ (1300, 0)માં છેદે છે.

પ્રશ્ન 3.
એક દિવસે 2 કિગ્રા સફરજન અને 1 કિગ્રા દ્રાક્ષની કિંમત ₹ 160 હતી. એક મહિના પછી 4 કિગ્રા સફરજન અને 2 કિગ્રા દ્રાક્ષની કિંમત ₹ 300 હતી. આ પરિસ્થિતિને બૈજિક રીતે અને ભૌમિતિક રીતે દર્શાવો.
ઉત્તરઃ
ધારો કે, 1 કિગ્રા સફરજનની કિંમત ₹ x અને 1 કિગ્રા દ્રાક્ષની કિંમત ₹ y છે.
આથી આપેલ માહિતી મુજબ, 2x + y = 160 અને 4x + 2y = 300.
આમ, સમીકરણો 2x + y = 160 અને 4x + 2y = 300 એ આપેલ પરિસ્થિતિને બેજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.
2x + y = 160

4x + 2y = 300

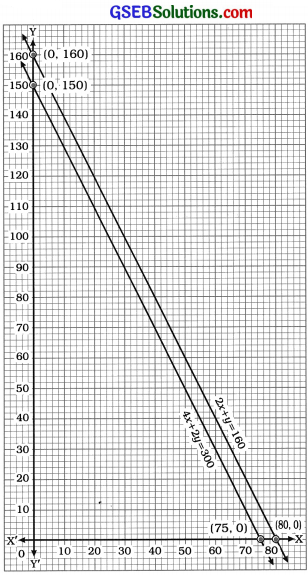
ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવે છે.
તમે જોઈ શકો છો કે, બંને રેખા પરસ્પર સમાંતર છે.