Gujarat Board GSEB Solutions Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2
Question 1.
Find the roots of the following quadratic equations by factorization method:
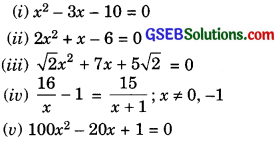
Solution:
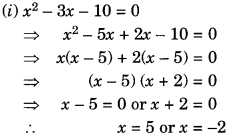
Hence, the roots of the given quadratic equation are 5 and – 2.

x = – 2 or x = \(\frac { 3 }{ 2 } \)
Hence, the roots of the given quadratic equation are – 2 and \(\frac { 3 }{ 2 } \)
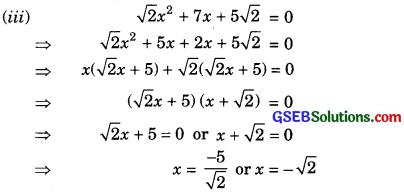
Hence, the roota of the given quadratic equation are – \(\frac { 5 }{ \sqrt { 2 } } \) and – \(\sqrt { 2 } \).
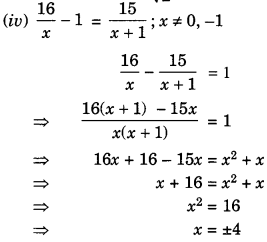

So, this root is repeated twice.
Hence, both the roots of the given quadratic equation are \(\frac { 1 }{ 10 } \).
![]()
Question 2.
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. Find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in ₹) was found to be 55 minus the number of articles produced in a day. On a particular day, the total cost of production was 750. Find out the number of toys produced on that day.
Solution.
(i) Let the number of marbles John had = x
Then, the number of marbles Jivanti had = (45 – x)
According to the given question,

Hence, if the number of marbles John had = 36,
then the number of marbles Jivanti had
= 45 – 36 = 9.
or, if the number of marbles John had = 9,
then the number of marbles Jivanti had = 45 – 9 = 36.
(ii) Let the number of toys produced on said
day = x and, cost of production – (55 – x)
According to the given question,
x (55 – x) = 750
55x – x2 – 750 = 0
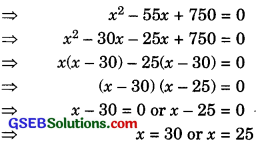
Hence, the number of toys produced on said day are 30 or 25.
![]()
Question 3.
Find two numbers whose sum is 27, and product is 182.
Solution:
Let the first number be x. So, second number = 27 – x.
According to question,

If x = 13 then other number = 27 – x
= 27 – 13 = 14
If x = 14 then other number = 27 – x
= 27 – 14 = 13
Hence, required two numbers are 13 and 14.
![]()
Question 4.
Find two consecutive positive integers, sum of whose square is 365.
Solution:
Let first positive integer be x.
So, other positive integer = x + 1
According to question,

Here x = – 14 does not exist.
Therefore, required positive integers are
x = 13 and x + 1 = 13 + 1 = 14.
Question 5.
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm. Find the other two sides.
Solution:
Let the base (BC) of the right triangle = x cm.
So, altitude (AB) = (x – 7) cm
and hypotenuse (AC) = 13 cm
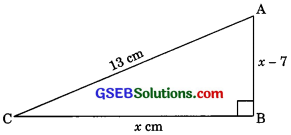
According to pythagoras theorem,

Since side of triangle is never negative.
So, x = 12
Now required sides of the triangle are
AB = x – 7
= 12 – 7 = 5 cm
BC = x = 12 cm.
![]()
Question 6.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produces on that day. If the total cost of production on that day was 90. Find the number of articles produced and cost of each articles.
Solution.
Let the number of articles produced be x.
Therefore, cost of production of each article
(in ₹) on that particular day = ₹ (2x + 3)
So, total cost of production that day = ₹ x (2x + 3)
According to question,

Since x = – \(\frac { 15 }{ 2 } \) is not possible.
So, x = 6
Hence, number of articles production be x = 6
and cost of production of each article
= ₹ (2x + 3)
= ₹ (2 x 6 + 3) = ₹ 15
![]()