GSEB Solutions Class 10 Maths Chapter 5 સમાંતર શ્રેણી Ex 5.2

Gujarat Board GSEB Solutions Class 10 Maths Chapter 5 સમાંતર શ્રેણી Ex 5.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 5 સમાંતર શ્રેણી Ex 5.2

પ્રશ્ન 1.
નીચેના કોષ્ટકમાં સમાંતર શ્રેણીનું પ્રથમ પદ વ, સામાન્ય તફાવત d અને n મું પદ a_n છે. ખાલી જગ્યા પૂરો:

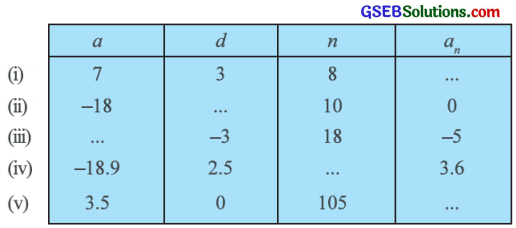
(i) અહીં, a = 7; d = 3; n = 8 અને a_n શોધવાનો છે.
a_n = a + (n – 1) d
a₈ = 7 + (8 – 1) 3 = 7 + 21 = 28

(ii) અહીં, a = – 18; n = 10; a_n = a₁₀ = 0 અને d શોધવાનો છે.
a_n = a + (n – 1) d
∴ 0 = – 18 + (10 – 1) d
∴ 18 = 9d
∴ d = 2

(iii) અહીં, d = – 3, n = 18, a_n = a₁₈ = – 5 અને a શોધવાનો છે.
a_n = a + (n – 1) a
∴ – 5 = a + (18 – 1) (- 3)
∴ 5 = a – 51
∴ a = 51 – 5
∴ a = 46

(iv) અહીં, a = – 18.9; d = 2.5; a_n = 3.6 અને n શોધવાનો છે.
a_n = a + (n – 1) d
3.6 = – 18.9 + (n – 1) (2.5)
22.5 = 2.5 (n – 1)
(n – 1) = \(\frac{22.5}{2.5}\)
∴ n – 1 = 9
∴ n = 10

(v) અહીં, a = 3.5; d = 0; n = 105 અને a_n શોધવાનો છે.
a_n = a + (n – 1) d
a₁₀₅ = 3.5 + (105 – 1) (0)
∴ a₁₀₅ = 3.5

પ્રશ્ન 2.
નીચેનામાંથી સાચો જવાબ શોધો અને ચકાસોઃ
(i) સમાંતર શ્રેણી 10, 7, 4, . નું 30મું પદ ………… છે.
(A) 97
(B) 77
(C) – 77
(D) – 87

(ii) સમાંતર શ્રેણી – 3, – \(\frac{1}{2}\), 2, .. નું 11મું પદ ……… છે.
(A) 28
(B) 22
(C) – 38
(D) – 48\(\frac{1}{2}\)

ઉત્તરઃ
(i) આપેલ સમાંતર શ્રેણી 10, 7, 4, .. માટે a = 10,
d = 7 – 10 = – 3 અને n = 30
a_n = a + (n – 1) d :
a₃₀ = 10 + (30 – 1) (- 3)
a₃₀ = 10 – 87
a₃₀ = – 77
આથી સાચો વિકલ્પ (C) – 77 છે.

(ii) આપેલ સમાંતર શ્રેણી -3, – \(\frac{1}{2}\), 2, . માટે
a = – 3, d = – \(\frac{1}{2}\) – (- 3) = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) અને
n = 11.
a_n = a + (n – 1) d
a₁₁ = – 3+ (11 – 1) (\(\frac{5}{2}\)).
a₁₁ = – 3 + 25
a₁₁ = 22
આથી સાચો વિકલ્પ (B) 22 છે.

પ્રશ્ન 3.
નીચેની સમાંતર શ્રેણીમાં ખાલી ખાનાનાં પદ શોધો :
(i) 2, , 26
(ii) , 13, , 3
(iii) 5, , , 9
(iv) -4,, , , , 6
(v) , 38, , , , – 22
ઉત્તરઃ
(i) આપેલ સમાંતર શ્રેણી માટે પ્રથમ પદ = a = 2 અને
ત્રીજું પદ = a + 2d = 26
a = 2 અને a + 2d = 26 પરથી d = 12 મળે.
હવે, બીજું પદ = a + d = 2 + 12 = 14
આમ, ખાલી ખાનામાં સંખ્યા મૂકતાં 14 મળે.

(ii) આપેલ સમાંતર શ્રેણી માટે,
બીજું પદ = a + d = 13 ………… (1)
ચોથું પદ = a + 3d = 3 …………(2)
સમીકરણો (1) અને (2)નો ઉકેલ શોધતાં વ = 18 અને d = – 5 મળે.
હવે, પ્રથમ પદ= a = 18 અને
ત્રીજું પદ = a + 2d = 18 + 2 (- 5) = 8
આમ, ખાલી ખાનાઓમાં સંખ્યાઓ મૂકતાં 18 અને [8] મળે.

વૈકલ્પિક રીતઃ
ધારો કે, આપેલ સમાંતર શ્રેણીના પ્રથમ ચાર પદ a₁, a₂, a₃, a₄ છે.
અહીં, a₂ = 13 અને a₄ = 3.
હવે, a₄ – a₃ = a₃ – a₂ = d
3 – a₃ = a₃ – 13
2a₃ = 16
a₃ = 8
વળી, a₂ – a₁ = a₃ – a₂
13 – a₁ = 8 – 13
13 – a₁ = – 5
a₁ = 18 આમ, ખાલી ખાનાઓમાં સંખ્યાઓ મૂકતાં 18 અને [8] મળે.

(iii) આપેલ સમાંતર શ્રેણી માટે,
પ્રથમ પદ = a = 5 …………..(1)
ચોથું પદ = a + 3d = 9 ………….(2)
સમીકરણ (1) અને (2) પરથી, d = 1 \(\frac{1}{2}\) અને a = 5 મળે.
હવે, બીજું પદ = a + d = 5 + 1 \(\frac{1}{2}\) = 6 \(\frac{1}{2}\)
અને ત્રીજું પદ = a + 2d = 5 + 2(\(\frac{1}{2}\)) = 8
આમ, ખાલી ખાનાઓમાં સંખ્યાઓ મૂકતાં 6\(\frac{1}{2}\) અને [8] મળે.

(iv) આપેલ સમાંતર શ્રેણી માટે,
પ્રથમ પદ = a = – 4 …………… (1)
છઠું પદ = a + 5d = 6 …………… (2)
સમીકરણ (1) અને (2) પરથી, a = – 4 અને d = 2 મળે.
હવે, બીજું પદ = a + d = (- 4) + 2 = – 2,
ત્રીજું પદ = a + 2d = (- 4) + 2 (2) = 0,
ચોથું પદ = a + 3d = (- 4) + 3 (2) = 2 અને
પાંચમું પદ = a + 4d = (- 4) + 4 (2) = 4.
આમ, ખાલી ખાનાઓમાં સંખ્યાઓ મૂકતાં, [0], [2] અને [4] મળે.

(v) આપેલ સમાંતર શ્રેણી માટે,
બીજું પદ = a + d = 38 ………. (1)
છઠું પદ = a + 5d = – 22 ………. (2)
સમીકરણ (1) અને (2) પરથી, d = – 15 અને a = 53 મળે.
હવે, પ્રથમ પદ = a = 53,
ત્રીજું પદ = a + 2d = 53 + 2 (- 15) = 23,
ચોથું પદ = a + 3d = 53 + 3 (- 15) = 8 અને
પાંચમું પદ = a + d = 53 + 4 (- 15) = – 7 મળે.
આમ, ખાલી ખાનામાં સંખ્યાઓ મૂકતા 53, 23, 8 અને – 7 મળે.

પ્રશ્ન 4.
સમાંતર શ્રેણી 3, 8, 13, 18, …નું કેટલામું પદ 78 થાય?
ઉત્તરઃ
ધારો કે સમાંતર શ્રેણી 3, 8, 13, 18, …નું nમું પદ 78 થાય.
અહીં, a = 3; d = 8 – 3 = 5; a = 78 અને n શોધવાનો છે.
a_n = a + (n – 1) d
78 = 3 + (n- 1) 5
75 = 5 (n – 1)
15 = n – 1
n = 16.
આમ, સમાંતર શ્રેણી 3, 8, 13, 18, .નું 10મું પદ 78 થાય.

પ્રશ્ન 5.
નીચેની સમાંતર શ્રેણીમાં પદોની સંખ્યા શોધોઃ
(i) 7, 13, 19, ……….., 205
(ii) 18, 15, 13, ………., – 47
ઉત્તરઃ
(i) આપેલ સાત્ત સમાંતર શ્રેણી 7, 13, 19, …………., 205 માટે a = 7, d = 13 – 7 = 6 અને અંતિમ પદ l = 205.
ધારો કે, શ્રેણીનું અંતિમ પદ nયું પદ છે.
a_n = a + (n – 1) d
205 = 7 + (n – 1) 6
198 = 6 (n – 1)
n – 1 = 33
n = 34
આમ, આપેલ સાત્ત સમાંતર શ્રેણીમાં 34 પદ છે.

(ii) આપેલ સાત્ત સમાંતર શ્રેણી 18, 15\(\frac{1}{2}\), 13, ……….., – 47
માટે વ = 18, d = 15\(\frac{1}{2}\) – 18 = – 2\(\frac{1}{2}\) = – \(\frac{5}{2}\) અને અંતિમ પદ l = – 47
. ધારો કે, શ્રેણીનું અંતિમ પદ nમું પદ છે.
a_n = a + (n – 1) d
– 47 = 18 + (n – 1) (3)
– 65 = – (n – 1)
n – 1 = 26
n = 27
આમ, આપેલ સાત્ત સમાંતર શ્રેણીમાં 27 પદ છે.

પ્રશ્ન 6.
શું સમાંતર શ્રેણી 11, 8, 5, 2 …નું કોઈ પદ – 150 હોઈ શકે?
ઉત્તરઃ
શક્ય હોય, તો ધારો કે સમાંતર શ્રેણી 11, 8, 5, 2, …નું nમું પદ – 150 છે.
અહીં, a = 11; d = 8 – 11 = – 3 અને
a_n = – 150
a_n = a + (n – 1) d
– 150 = 11 + (n – 1) (- 3)
– 161 = – 3(n – 1)
n – 1= \(\frac{161}{3}\)
n = \(\frac{164}{3}\)
પરંતુ, n એ સમાંતર શ્રેણીના પદનો ક્રમાંક હોવાથી ધન પૂર્ણાક જ હોય. આથી સમાંતર શ્રેણી 11, 8, 5, 2, …નું કોઈ પણ પદ – 150 ન હોઈ શકે.

પ્રશ્ન 7.
સમાંતર શ્રેણીનું 11મું પદ 38 અને 16મું પદ 73 હોય, તો તેનું 31મું પદ શોધો.
ઉત્તરઃ
કોઈ પણ સમાંતર શ્રેણી માટે
a_n = a + (n – 1) d
a₁₁ = a + 10 d
a + 10 d = 38 ………….(1)
a₁₆ = a + 15d
a + 15 d = 73 ………….(2)
સમીકરણ (1) અને (2) પરથી,
d = 7 અને a = – 32 મળે.
હવે, 31મું પદ = a₃₁ = a + 30 d
= – 32 + 30 (7)
= – 32 + 210
= 178
આમ, આપેલ સમાંતર શ્રેણીનું 31મું પદ 178 છે. ‘ નોંધઃ d = \(\frac{a_{16}-a_{11}}{16-11}=\frac{73-38}{5}=\frac{35}{5}\) = 7 દ્વારા પણ તે સહેલાઈથી મેળવી શકાય.

પ્રશ્ન 8.
એક સમાંતર શ્રેણીમાં 50 પદ છે. જો ત્રીજું પદ 12 અને છેલ્લે ૬ પદ 106 હોય, તો તેનું 29મું પદ શોધો.
ઉત્તરઃ
આપેલ સાન્ત સમાંતર શ્રેણીમાં 50 પદ છે અને તેનું છેલ્લું પદ 106 છે.
a₅₀ = 106 અને a₃ = 12
હવે, a_n = a + (n – 1) d
a₃ = a + 2d = 12 ………..(1)
અને a₅₀ = a + 49d = 106 ………..(2)
સમીકરણ (1) અને (2) પરથી,
d = 2 અને a = 8 મળે.
હવે, 29મું પદ = a₂₉ = a + 28d
a₂₉ = 8 + 28 (2).
a₂₉ = 64
આમ, આપેલ સાત્ત સમાંતર શ્રેણીનું 29મું પદ 64 છે.

પ્રશ્ન 9.
જો સમાંતર શ્રેણીનું ત્રીજું અને નવમું પદ અનુક્રમે 4 અને – 8 હોય, તો તે શ્રેણીનું કયું પદ 0 થાય?
ઉત્તરઃ
આપેલ સમાંતર શ્રેણી માટે a₃ = 4 અને a₉ = – 8
હવે, a_n = a + (n – 1) d
a₃ = a + 2d = 4 ……. (1)
અને a₉ = a + 8d = – 8
સમીકરણ (1) અને (2) પરથી, d = – 2 અને a = 8 મળે.
ધારો કે, સમાંતર શ્રેણીનું nમું પદ 0 છે.
a_n = a + (n – 1)d
0 = 8 + (n – 1) (- 2)
2 (n – 1) = 8
n – 1 = 4
n = 5
આમ, આપેલ સમાંતર શ્રેણીનું 5મું પદ 0 હોય.

પ્રશ્ન 10.
કોઈ સમાંતર શ્રેણીમાં 17મું પદ 10મા પદ કરતાં 7 વધુ છે. તેનો સામાન્ય તફાવત શોધો.
ઉત્તરઃ
આપેલ સમાંતર શ્રેણી માટે,
a₁₇ = a₁₀ + 7
a + 16d = a + 9d + 7 (∵ a_n = a + (n-1) d)
7d = 7
d = 1
આમ, આપેલ સમાંતર શ્રેણીનો સામાન્ય તફાવત 1 છે.

પ્રશ્ન 11.
સમાંતર શ્રેણી 3, 16, 27, 19, -નું કયું પદ 54માં પદ કરતાં 132 વધુ હશે?
ઉત્તરઃ
આપેલ સમાંતર શ્રેણી 3, 15, 27, 19, … માટે,
a = 3 અને d = 15 – 3 = 12.
ધારો કે, સમાંતર શ્રેણીનું nમું પદ તેના 54માં પદ કરતાં 132 વધુ છે.
a_n = a₅₄ + 132
a + (n – 1) d = 9 + 53d + 132
3 + (n – 1) (12) = 3 + 53 (12) + 132
12 (n – 1) = 12 (53 + 11)
12 (n – 1) = 12 x 64
n – 1 = 64
∴ n = 65
આમ, આપેલ સમાંતર શ્રેણીનું 65મું પદ તેના 54મા પદ કરતાં 132 વધુ હોય.

પ્રશ્ન 12.
બે સમાંતર શ્રેણીના સામાન્ય તફાવત સમાન છે. તેમના 100માં પદનો તફાવત 100 હોય, તો 1000મા પદનો તફાવત કેટલો હશે?
ઉત્તરઃ
ધારો કે, બે સમાંતર શ્રેણીઓના પ્રથમ પદ અનુક્રમે a₁ અને a₂ (a₁ > a₂) છે અને તેમનો સમાન સામાન્ય તફાવત d છે.
સમાંતર શ્રેણી માટે તમું પદ a_n = a + (n – 1) d
તો, પ્રથમ સમાંતર શ્રેણીનું 100મું પદ = a₁ + 99d અને
બીજી સમાંતર શ્રેણીનું 100મું પદ = a₂ + 99d
તેમના 100મા પદનો તફાવત 100 છે.
∴ (a₁ + 99d) – (a₂ + 99d) = 100 (∵ a₁ > a₂)
∴ a₁ – a₂ = 100 …….. (1)
હવે, પ્રથમ સમાંતર શ્રેણીનું 1000મું પદ = a₁ + 999d
અને બીજી સમાંતર શ્રેણીનું 1000મું પદ = a₂ + 999d
આથી તેમના 1000મા પદનો તફાવત = (a₁ + 999d) – (a₂ + 999d)
= a₁ – a₂ = 100 ((1) મુજબ
આમ, આપેલ સમાંતર શ્રેણીઓના 1000મા પદનો તફાવત 100 છે.

પ્રશ્ન 13.
ત્રણ અંકની કેટલી સંખ્યા 7 વડે વિભાજ્ય હશે?
ઉત્તરઃ
ત્રણ અંકની 7 વડે વિભાજ્ય સંખ્યાઓની યાદી નીચે મુજબ છે: 105, 112, 119, … 987, 994
આ યાદી એક સાત્ત સમાંતર શ્રેણી રચે છે. જેમાં a = 105, d = 112 – 105 = 7 અને અંતિમ પદ l = 994 છે.
ધારો કે, અંતિમ પદ એ શ્રેણીનું nમું પદ છે.
l = a_n
994 = a + (n – 1) d
994 = 105 + (n – 1) 7
7 (n – 1) = 889
n – 1 = 127
∴ n = 128
આથી દર્શાવેલ સાત્ત સમાંતર શ્રેણીમાં કુલ 128 પદ છે. આથી ત્રણ અંકની 128 સંખ્યાઓ 7 વડે વિભાજ્ય હોય.

પ્રશ્ન 14.
10 અને 250 વચ્ચે 4ના કેટલા ગુણિત હશે?
ઉત્તરઃ
10 અને 250 વચ્ચેના 4ના ગુણિતો નીચેની યાદી રચે છે: 12, 16, 20, …, 244, 248
આ યાદી એક સાન્ત સમાંતર શ્રેણી રચે છે, જેમાં વ = 12, d = 16- 12 = 4 અને અંતિમ પદ l = 248 છે.
ધારો કે, અંતિમ પદ એ શ્રેણીનું nમું પદ છે.
l = a_n
l = a + (n – 1) d
248 = 12 + (n – 1) 4
236 = 4 (n – 1)
n – 1 = 59
n = 60
આથી દર્શાવેલ સાત્ત સમાંતર શ્રેણીમાં કુલ 60 પદ છે. આથી 10 અને 250ની વચ્ચે 4ના 60 ગુણિત છે.

પ્રશ્ન 15.
nના કયા મૂલ્ય માટે બે સમાંતર શ્રેણીઓ 63, 65, 67, …. અને 3, 10, 17, ……… ના તમા પદ સમાન થાય?
ઉત્તરઃ
પહેલી સમાંતર શ્રેણી 63, 65, 67, … માટે, a = 63 અને d = 65 – 63 = 2. તો,
પહેલી સમાંતર શ્રેણીનું nમું પદ
a_n = a + (n – 1) d = 63 + (n – 1) (2) થાય.
બીજી સમાંતર શ્રેણી 3, 10, 17, . માટે,
A = 3, D = 10 – 3 = 7
તો બીજી સમાંતર શ્રેણીનું nમું પદ = A_n = A + (n – 1) D
= 3 + (n – 1) (7) થાય.
હવે, a_n = A_n
63 + (n – 1) (2) = 3 + (n – 1) (7)
63 – 3 = (n – 1) (7 – 2)
60 = 5 (n – 1)
n – 1 = 12
n = 13
આમ, n = 13, માટે આપેલ બે સમાંતર શ્રેણીઓના તમા પદ સમાન થાય.

પ્રશ્ન 16.
એવી સમાંતર શ્રેણી શોધો કે જેનું ત્રીજું પદ 16 અને 7મું પદ 6મા પદથી 12 વધુ હોય.
ઉત્તરઃ
માગેલ સમાંતર શ્રેણી માટે a₃ = 16 અને a₇ = a₅ + 12.
કોઈ પણ સમાંતર શ્રેણી માટે a_n = a + (n – 1) d
a + 2d = 16 અને સ્વ a + 6d = a + 4d + 12
a + 6d = a + 4d + 12 પરથી 2d = 12,
એટલે કે, d = 6 મળે.
a + 2d = 16માં d = 6 મૂકતાં a = 4 મળે.
આથી, માગેલ સમાંતર શ્રેણી 4, 4 + 6, 4 + 2 (6), 4 + 3 (6), … છે.
આમ, માગેલ સમાંતર શ્રેણી 4, 10, 16, 22, …. છે.

પ્રશ્ન 17.
સમાંતર શ્રેણી 3, 8, 13, , 253 હોય તો તેનું છેલ્લેથી 20મું પદ શોધો.
ઉત્તરઃ
આપેલ સાન્ત સમાંતર શ્રેણી 3, 8, 13, , 253 માટે a = 3, d = 8 – 3 = 5 અને અંતિમ પદ l = 253.
ધારો કે, અંતિમ પદ એ શ્રેણીનું nમું પદ છે.
l = a_n
l = a + (n – 1) d
253 = 3 + (n – 1) (5)
250 = 5 (n – 1)
n – 1 = 50
n = 51
આમ, આપેલ સાત્ત સમાંતર શ્રેણીમાં કુલ 51 પદ છે.
હવે, શ્રેણીનું છેલ્લેથી 20મું પદ = શ્રેણીનું શરૂઆતથી (51 – 20 + 10મું પદ)= 32મું પદ
a₃₂ = a + 31d
a₃₂ = 3 + 31 (5)
a₃₂ = 158
આમ, આપેલ સાન્ત સમાંતર શ્રેણીનું છેલ્લેથી 20મું પદ 158 છે.

પ્રશ્ન 18.
એક સમાંતર શ્રેણીનાં ચોથા અને આઠમા પદનો સરવાળો 24 છે. અને છઠ્ઠા અને દસમા પદનો સરવાળો 44 છે. આ સમાંતર શ્રેણીનાં પ્રથમ ત્રણ પદ શોધો.
ઉત્તરઃ
કોઈ પણ સમાંતર શ્રેણી માટે a_n = a + (n – 1) d
a₄ = a + 3d,
a₈ = a + 7d,
a₆ = a + 5d અને
a₁₀= a + 9d
હવે, a₄ + a₈ = 24 (આપેલ માહિતી મુજબ)
(a + 3d) + (a + 74) = 24
2a + 10d = 24
a + 5d = 12 ………… (1)
વળી, a₆ + a₁₀ = 44 (આપેલ માહિતી મુજબ)
(a + 5d) + (a + 9d) = 44
2a + 14d = 44
a + 70 = 22 ………… (2)
સમીકરણ (1) અને (2) પરથી d = 5 અને a =- 13 મળે.
આથી a₂ = a + d = – 13 + (5) = – 8 અને
a₃ = a + 2d = – 13 + 2 (5) = – 3.
આમ, સમાંતર શ્રેણીનાં માગેલ પ્રથમ ત્રણ પદ – 13, -8, -3 છે.

પ્રશ્ન 19.
સુબ્બા રાવે 1995માં ૨ 5000ના વાર્ષિક વેતનથી કામ શરૂ કર્યું અને તેમને દર વર્ષે ૨200ની વેતન વૃદ્ધિ મળે છે. કયા વર્ષે તેમનું વેતન 7000 થશે?
ઉત્તરઃ
સુષ્મા રાવની પ્રથમ વર્ષની આવક =₹ 5000
તેની બીજા વર્ષની આવક = ₹ 5000 + ₹ 200 = ₹ 5200
તેની ત્રીજા વર્ષની આવક = ₹ 5200 + ₹ 200 = ₹ 5400
તેની આવકના આ આંકડા (૪માં) સમાંતર શ્રેણી 5000, 5200, 5400, … રચે છે.
અહીં, a = 5000; d = 5200 – 5000 = 200; a_n = 7000 અને 1 શોધવાનો છે.
a_n = a + (n – 1) d
7000 = 5000 + (n – 1) (200)
2000 = 200 (n – 1)
n – 1 = 10
n = 11
આમ, 11મા વર્ષે એટલે કે વર્ષ 2005માં સુષ્મા રાવનું વેતન ₹ 7000 થશે.

પ્રશ્ન 20.
રામકલી વર્ષના પ્રથમ અઠવાડિયે ₹ 5 ની બચત કરે છે. અને પછી તેની અઠવાડિક બચતમાં ₹ 1.75 નો વધારો કરે છે. જો તમાં અઠવાડિયે તેની બચત ₹ 20.75 હોય, તો તનું મૂલ્ય શોધો.
ઉત્તરઃ
રામકલીની પહેલા અઠવાડિયાની બચત = ₹ 5
તેની બીજા અઠવાડિયાની બચત = ₹ 5 + ₹ 1.75 = ₹ 6.75
તેની ત્રીજા અઠવાડિયાની બચત = ₹ 6.75 + ₹ 1.75 = ₹ 8.50
આમ, રામકલીની અઠવાડિક બચતના આંકડા (₹ માં) સમાંતર શ્રેણી 5, 6.75, 8.50, … રચે છે.
અહીં, a = 5; d = 6.75 – 5 = 1.75; a_n = 20.75 અને n શોધવાનો છે.
a_n = a + (n – 1) d
20.75 = 5 + (n – 1) (1.75)
1.75 (n – 1) = 15.75
n – 1 = 9
n = 10.
આમ, જો રામકલીની તમા અઠવાડિયે બચત 20.75 હોય, તો n = 10.