GSEB Solutions Class 10 Maths Chapter 6 ત્રિકોણ Ex 6.6

Gujarat Board GSEB Solutions Class 10 Maths Chapter 6 ત્રિકોણ Ex 6.6 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 6 ત્રિકોણ Ex 6.6

આ સ્વાધ્યાય પરીક્ષા માટે ધ્યાનમાં લેવાનો નથી.

પ્રશ્ન 1.
આપેલ આકૃતિમાં, PS એ ∆ PQRના ∠QPRનો દ્વિભાજક છે. સાબિત કરો કે, \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\).

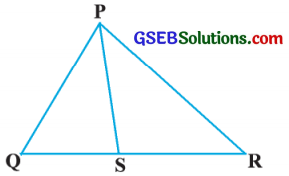
ઉત્તરઃ

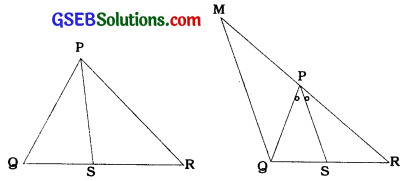
રચના: ઉમાંથી PSને સમાંતર રેખા દોરો, જે લંબાવેલ RPને Mમાં છેદે છે.
સાબિતી: ∆ MORમાં બિંદુઓ P અને s અનુક્રમે MR અને QRનાં બિંદુઓ છે તથા PS || MQ.

\(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{MP}}{\mathrm{PR}}\) (પ્રમેય 6.1) ……… (1)

હવે, PS || MQ અને PQ તેમની છેદિકા છે.
∠SPQ = ∠PQM (યુગ્મકોણ) …… (2)
તે જ રીતે, PS || MQ અને NR તેમની છેદિકા છે.
∴ ∠RPS = ∠PMQ (અનુકોણ) …………. (3)
PS એ ∠QPRનો દ્વિભાજક છે.
∴ ∠SPQ = ∠RPS …………… (4)
(2), (3) અને (4) પરથી,
∴ PQM = ∠PMQ
∆ PMQમાં, MP = PQ …………… (5)
(1) અને (5) પરથી,

\(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\)

પ્રશ્ન 2.
આપેલ આકૃતિમાં ∆ ABCમાં BD ⊥ AC, DM ⊥ BC અને DN ⊥ AB થાય તેવું બિંદુ D કર્ણ AC પર છે. સાબિત કરો કે,

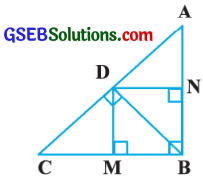
(i) DM² = DN . MC
(ii) DN² = DM . AN
ઉત્તરઃ
યતુષ્કોણ DMBNમાં, ∠B = ∠M = ∠N = 90°.
આથી DMBN લંબચોરસ છે.
DN = MB ………….(1)
અને DM = NB ………….(2)
હવે, BD ⊥ AC
∴ ∠BDC = 90° અને ∆ BDC કાટકોણ ત્રિકોણ છે, જેમાં DM એ કર્ણ BC પરનો વેધ છે.
આથી ∆ BMD ~ ∆ DMC ~ ∆ BDC (પ્રમેય 6.7)
∴ \(\frac{\mathrm{DM}}{\mathrm{CM}}=\frac{\mathrm{BM}}{\mathrm{DM}}\)
∴ DM² = BM . CM
∴ DM² = DN . MC ((1) પરથી DN = MB) (પરિણામ (10)
તે જ રીતે, ∆ ADB કાટકોણ ત્રિકોણ છે. જેમાં DN એ કર્ણ AB પરનો વેધ છે.
∆ AND ~ ∆ DNB ~ ∆ ADB (પ્રમેય 6.7)
∴ \(\frac{\mathrm{DN}}{\mathrm{BN}}=\frac{\mathrm{AN}}{\mathrm{DN}}\)
∴ DN² = BN · AN
∴ DN² = DM · AN ((2) પરથી DM = NB) (પરિણામ (2))

પ્રશ્ન 3.
આપેલ આકૃતિમાં, ∆ ABCમાં, ∠ABC > 90° અને AD ⊥ લંબાવેલ CB. સાબિત કરો કે, AC² = AB² + BC² + 2 BC . BD.

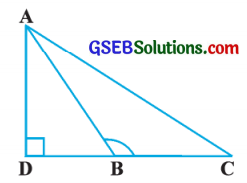
ઉત્તરઃ
∆ ADCમાં, ∠D = 90°
AC² = AD² + DC²
∴ AD² = AC² – DC² ……….. (1)
∆ ADBમાં, ∠D = 90°
AB² = AD² + DB²
∴ AD² = AB² – DB² …………. (2)
(1) અને (2) પરથી,
AC² – DC² = AB² – DB²
AC² = AB² + DC² – DB²
AC² = AB² + (BC + DB)² – DB²
AC² = AB² + BC² + 2BC · DB + DB² – DB²
∴ AC² = AB² + BC² + 2BC · BD

પ્રશ્ન 4.
આપેલ આકૃતિમાં, ∆ ABCમાં, ∠ABC < 90° અને AD⊥BC છે. સાબિત કરો કે, AC² = AB² + BC² – 2BC · BD.

ઉત્તરઃ
∆ ADCમાં, ∠D = 90°
∴ AC² = AD² + CD²
∴ AD² = AC² – CD² …………….. (1)
∆ ADBમાં, ∠D = 90°
∴ AB² = AD² + BD²
∴ AD² = AB² – BD² ……………. (2)
(1) અને (2) પરથી,
AC² – CD² = AB² – BD²
AC² = AB² + CD² – BD²
AC² = AB² + (BC – BD)² – BD²
∴ AC² = AB² + BC² – 2BC · BD + BD² – BD²
∴ AC² = AB² + BC² – 2BC · BD

પ્રશ્ન 5.
આપેલ આકૃતિમાં, AD એ ∆ ABCની મધ્યગા અને AM ⊥ BC સાબિત કરો કે,
(i) AC² = AD² + BC · DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(ii) AB² = AD² – BC . DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\) BC²

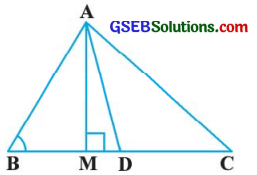
ઉત્તરઃ
અહીં, ∆ AMD, ∆ AMC અને ∆ AMB કાટકોણ ત્રિકોણો છે.
વળી, AD મધ્યગા હોવાથી, D એ BCનું મધ્યબિંદુ છે.
CD = BD = \(\frac{\mathrm{BC}}{2}\)
વળી, DM = CM – CD અને DM = BD – BM

(i) ∆ AMC માં, ∠M = 90°
AC² = AM² + CM²
AC² = AM² + (DM + CD)²
AC² = AM² + DM² + 2 DM CD + CD²
AC² = (AM² + DM²) + (2CD) (DM) + CD²
AC² = AD² + BC . DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(∵ ∆ AMDમાં, AD² = AM² + DM²)

(ii) ∆ AMBમાં, ∠M = 90°
AB² = AM² + BM²
AB² = AM² + (BD – DM)²
AB² = AM² + BD² – 2 . BD . DM + DM²
AB² = (AM² + DM²) – (2BD) (DM) + BD²
AB² = AD² – BC . DM + (\(\left(\frac{\mathrm{BC}}{2}\right)^{2}\))
(∵ ∆ AMDમાં, AD² = AM² + DM²)

(iii) વિભાગ (1) અને (2) નાં પરિણામોનો સરવાળો લેતાં,
AC² + AB² = AD² + BC · DM + (\(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)) + AD² – BC DM + (\(\left(\frac{\mathrm{BC}}{2}\right)^{2}\))
AC² + AB² = 2AD² + 2 \(\left(\frac{\mathrm{BC}^{2}}{4}\right)\)
AC² + AB² = 2AD² + \(\frac{1}{2}\) BC²
[નોંધઃ વિભાગ (3)ના પરિણામમાં BCના સ્થાને 2BD
લેતાં, આપણને અતિ પ્રખ્યાત એપોલોનિસ પ્રમેય મળે જેનું વિધાન નીચે મુજબ છેઃ જો AD એ ∆ ABCની મધ્યમા હોય, તો
AB² + AC² = 2 (AD² + BD²).]

પ્રશ્ન 6.
સાબિત કરો કે, સમાંતરબાજુ ચતુષ્કોણના વિકર્ણોના વર્ગોનો સરવાળો તેની બાજુઓના વર્ગોના સરવાળા જેટલો હોય છે. સૌપ્રથમ આપણે ઍપોલોનિસ પ્રમેય સાબિત કરીએ.
ઉત્તરઃ

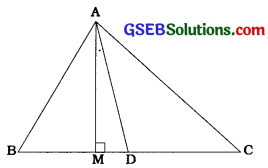
આકૃતિમાં દર્શાવ્યા મુજબ, ∆ ABCમાં AD મધ્યગા અને AM વેધ છે.
આથી AB² + AC² = AM² + BM² + AM²+ CM²
= 2AM² + (BD – MD)² + (CD + MD)²
= 2AM² + (BD – MD)² + (BD + MD)²
(∵ CD = BD)
= 2 AM² + 2BD² + 2MD²
= 2 (AM² + MD²) + 2BD²
= 2 AD² + 2BD²
∴ AB² + AC² = 2 (AD² + BD²)

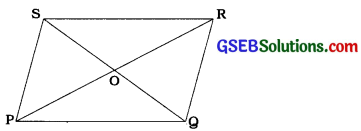
ધારો કે, સમાંતરબાજુ ચતુષ્કોણ PQRSના વિકણ પરસ્પર 0 બિંદુમાં દુભાગે છે.
આથી PO = RO = \(\frac{1}{2}\) PR અને
QO = SO = \(\frac{1}{2}\)
હવે, ∆ PQRમાં, QO મધ્યગા છે.
PQ² + QR² = 2 (QO² + PO²)

PQ² + QR² = \(2\left\{\left(\frac{\mathrm{QS}}{2}\right)^{2}+\left(\frac{\mathrm{PR}}{2}\right)^{2}\right\}\)

PQ² + QR² = \(\frac{1}{2}\) (QS² + PR²) …….. (1)
તે જ રીતે,
∆ QRSમાં, QR² + RS² = \(\frac{1}{2}\) (QS² + PR²) …………(2)
∆ RSPમાં, RS² + SP² = \(\frac{1}{2}\) (QS² + PR²) ………….. (3)
∆ SPOમાં, SP² + PQ² = \(\frac{1}{2}\) (QS² + PR²) ………….. (4)
(1), (2), (3) અને (4)નો સરવાળો લેતાં,
2 (PQ²+ QR² + RS² + SP²) = 2 (QS² + PR²)
∴ PQ² + QR² + RS² + SP² = QS² + PR²
આમ, સમાંતરબાજુ ચતુષ્કોણના વિકણોના વર્ગોનો સરવાળો તેની બાજુઓના વર્ગોના સરવાળા જેટલો હોય છે.

પ્રશ્ન 7.
આપેલ આકૃતિમાં, બે જીવાઓ AB અને CD એકબીજાને બિંદુ Pમાં છેદે છે. સાબિત કરો કે,
(i) ∆ ARC ~ ∆ DPB
(ii) ∆ PPB = CP . DP.

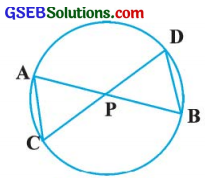
ઉત્તરઃ
અહીં, ∠CAB = ∠CDB (એક જ વૃત્તખંડના ખૂણા)
∠CAP = ∠BDP
તે જ રીતે, ∠ACD = ∠DBA (એક જ વૃત્તખંડના ખૂણા)
∴ ∠ACP = ∠DBP
હવે, ∆ APC અને ∆ DPBમાં,
∠CAP = ∠BDP અને ∠ACP = ∠DBP
ખૂબૂ શરત મુજબ, ∆ APC ~ ∆ DPB (પરિણામ 1)
∴ AP . PB = CP . DP (પરિણામ 2)

પ્રશ્ન 8.
આપેલ આકૃતિમાં, એક વર્તુળની બે જીવાઓ AB અને CD (લંબાવીએ તો) વર્તુળના બહારના ભાગમાં એકબીજાને Pમાં છેદે છે. સાબિત કરો કે,
(i) ∆ PAC ~ ∆ PDB
(ii) PA . PB = PC . PD

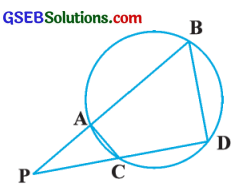
ઉત્તરઃ
ચક્રીય ચતુષ્કોણ ACDBમાં,
∠ACD + ∠ABD = 180°
વળી, ∠ACD + ∠ACP = 180° (રખિક જોડના ખૂણા).
∠ABD = ∠ACP
∠PBD = ∠PCA.
તે જ રીતે, ∠CAB + ∠CDB = 180° (ચક્રીય ચતુષ્કોણ)
∠CAB + ∠CAP = 180° રિખિક જોડના ખૂણા)
∠CDB = ∠CAP
∠PDB = ∠PAC
હવે, ∆ PDB અને ∆ PACમાં,
∠PBD = ∠PCA
∠PDB = ∠PAC
ખૂબું શરત મુજબ, ∆ PAC ~ ∆ PDB (પરિણામ (1)).
∴ \(\frac{\mathrm{PA}}{\mathrm{PD}}=\frac{\mathrm{PC}}{\mathrm{PB}}\)
∴ PA . PB = PC . PD (પરિણામ (2))

પ્રશ્ન 9.
આપેલ આકૃતિમાં, D એ ત્રિકોણ ABC ની બાજુ BC પરનું એવું બિંદુ છે કે જેથી \(\frac{\mathbf{B D}}{\mathbf{C D}}=\frac{\mathbf{A B}}{\mathbf{A C}}\) સાબિત કરો કે, AD એ ∠BACનો દ્વિભાજક છે.

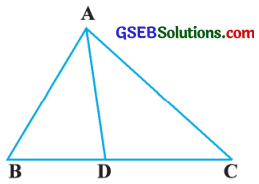
ઉત્તરઃ
B માંથી ADને સમાંતર રેખા દોરો, જે લંબાવેલ CAને Pમાં છેદે છે.
હવે, ∆ PBCમાં, A અને D અનુક્રમે PC અને BC પરનાં બિંદુઆો છે તથા PB || AD.
∴ \(\frac{\mathrm{PA}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{CD}}\)
વળી, \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) (આપેલ છે.)
∴ PA = AB.
હવે, ∆ PABમાં, PA = AB
∴ ∠ABP = ∠APB ………… (1)
AD || BP અને AB તેમની છેદિકા છે.
∴ ∠ABP = ∠BAD (યુગ્મકોણ) …………..(2)
AD || BP અને CP તેમની છેદિકા છે.
∠APB = ∠CAD (અનુકોણ) …………….(3)
(1), (2) અને (3) પરથી,
∠BAD = ∠CAD
વળી, ∠BAD + ∠CAD = ∠BAC.
આથી AD એ ∠BAC નો દ્વિભાજક છે.

પ્રશ્ન 10.
નાઝીમા પાણીના પ્રવાહમાં માછલીઓ પકડી રહી છે. તેનો માછલી પકડવાનો સળિયાનો હૂક પાણીની સપાટીથી 1.8 મીટર ઊંચે છે અને દોરીના નીચેના છેડા પરનો આંકડો પાણીની સપાટી પર એવી રીતે સ્થિર છે કે નાઝીમાથી તેનું અંતર 3.6 મીટર છે અને સળિયાના હૂક નીચેની પાણીની સપાટીથી તેનું અંતર 2.4 મીટર છે. એવું માની લઈએ કે (સળિયાના હૂકથી આંકડા સુધી) તેની દોરી તંગ છે, તો તેણે કેટલી દોરી બહાર કાઢી છે? (જુઓ આપેલ આકૃતિ) જો તે દોરીને 5 સેમી / સેના દરથી અંદર ખેંચે, તો 12 સેકન્ડ પછી નાઝીમાનું આંકડાથી સમક્ષિતિજ અંતર કેટલું હશે?

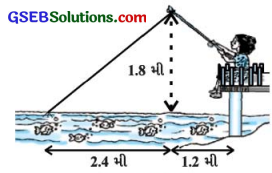
ઉત્તરઃ

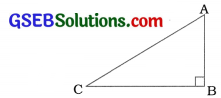
અહીં, ∆ ABC એ મૂળ સ્થિતિ દર્શાવે છે જેમાં A માછલી પકડવાના સળિયાનો હૂક છે, C દોરીના નીચેના છેડા પરનો આંકડો છે અને B સળિયાના હૂકની નીચેનું પાણી પરનું બિંદુ છે.
તો, ∆ ABCમાં, ∠B = 90° , AB = 1.8 મી અને BC = 2.4 મી.
હવે, AC² = AB² + BC² (પાયથાગોરસ પ્રમેય)
AC² = (1.8)² + (2.4)²
AC² = 3.24 + 5.76
AC² = 9
AC = 3 મી
આમ, મૂળ સ્થિતિમાં તેણે ૩મી દોરી બહાર કાઢી છે.
1 સેકન્ડમાં અંદર ખેંચેલ દોરીની લંબાઈ = 5 સેમી
12 સેકન્ડમાં અંદર ખેંચેલ દોરીની લંબાઈ = 60 સેમી = 0.6 મી
હવે, બીજી સ્થિતિમાં, દોરીની લંબાઈ AC = 3મી – 0.6 મી = 2.4 મી
અને AB = 1.8 મી.
ફરીથી, AC² = AB² + BC²
(2.4)² = (1.8)² + BC²
BC² = (2.4)² – (1.8)²
BC² = (2.4 + 1.80 (2.4 – 1.8).
BC² = 4.2 x 0.6
BC² = 2.52
∴ BC = \(\sqrt{2.52}\)
∴ BC = 1.59 મી (આશરે)
હવે, નાઝીમાનું આંકડાથી સમક્ષિતિજ અંતર = BC + 1.2 મી = (1.59 + 1.20 મી = 2.79 મી