GSEB Solutions Class 10 Science Chapter 12 Electricity

Gujarat Board GSEB Textbook Solutions Class 10 Science Chapter 12 Electricity Textbook Questions and Answers, Additional Important Questions, Notes Pdf.

Gujarat Board Textbook Solutions Class 10 Science Chapter 12 Electricity

Gujarat Board Class 10 Science Electricity InText Questions and Answers

Question 1.
What does an electric circuit mean?
Answer:
A continuous conducting path consisting of wires and other resistances and a switch between the two terminals of a cell or a battery along which an electric current flow is called a circuit.

Question 2.
Define the unit of current.
Answer:
The unit of current is Ampere. 1 Ampere current is said to be there when 1 coulomb of charge flows through any cross-section of a conductor in 1 second.

Question 3.
Calculate the number of electrons constituting one coulomb of charge.
Answer:
1C = charge contained in 6 x 10¹⁸ electrons.

Question 4.
Name a device that helps to maintain a potential difference across a conductor.
Answer:
A battery of many cells or a single cell can maintain a potential difference.

Question 5.
What is meant by saying that the potential difference between two points is I V?
Answer:
The potential difference between two points is said to be 1 V if I Joule of work is done in moving 1 Coulomb of charge from one point to another point.

Question 6.
How much energy is given to each coulomb of charge passing through a 6 V battery?
Answer:
Amount of charge = 1 coulomb or 1C
Potential difference = 6 V
Energy or work done = ?
Work done or energy = V x Q  [Q is the amount of charge flowing between two points at potential difference V = 6]
i.e = V x Q
W = 6 x 1 Work done or energy = 6 joules.

Question 7.
On what factors do the resistance of a conductor depend?
Answer:
The resistance of a conductor depends on:
(a) Length of a conductor: Resistance of a conductor is directly proportional to the length of a conductor. If length increases resistance will also increase.
(b) Areaofcrosssectlonofaconductor: The resistance of a conductor is inversely proportional to the area of the cross-section of a conductor.

(c) Effect of the material of a conductor: The resistance of a conductor also depends on the material of a conductor.
E.g. The resistance of nichrome wire is 60 times more than that of copper wire as nichrome has high electrical resistance.
(d) Effect of temperature: The resistance of all pure metals increases on increasing the temperature and decreases on decreasing the temperature.

Question 8.
Will current flow more easily through a thick wire or a thin wire of the same material, when connected to the same source? Why?
Answer:
The current will flow more easily through a thick wire as compared to the thin wire because the resistance of a thick wire is less than that of thin wire. Less resistance means more current.

Question 9.
Let the resistance of an electrical component remains constant while the potential difference across the two ends of the component decreases to half of its former value. What change will occur -in the current through it?
Answer:
The amount of current will be halved.

Question 10.
Why are coils of electric toasters and electric irons made of an alloy rather than a pure metal?
Answer:
The coils of such heating appliances are made up of an alloy rather than a pure metal because:
(a) The resistivity of an alloy is much higher than that of pure metal.
(b) An alloy does not undergo oxidation easily even at high temperatures when it is even red hot.

Question 11.
(a) Which among iron and mercury is a better conductor?
(b) Which material is the best conductor?
Answer:
(a) Iron
(b) Silver

Question 12.
Draw a schematic diagram of a circuit consisting of a battery of three cells of 2 V each, a 5 Ω resistor, 8 Ω resistors, and a 12 Ω resistor, and a plug key, all connected in series.
Answer:

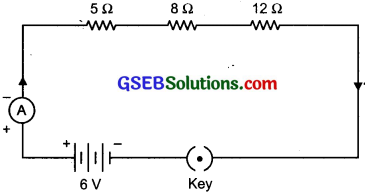
Question 13.
Redraw the circuit of Question 12, putting in an ammeter to measure the current through the resistors and a voltmeter to measure the potential difference across the 12 Ω resistors. What would be the readings in the ammeter and the voltmeter?
Answer:

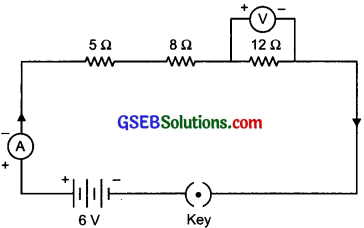
R = 5Ω + 8Ω + 12Ω = 25 Ω
V = 6V
I = ?
I = \(\frac{V}{R_{s}}\) = \(\frac {6V}{25 Ω}\) = 0.24 A
When R = 12 Ω
V = IR = 0.24 x 12 = 2.88 V
Hence, the reading in the ammeter would be 0.24 A, and the reading in the voltmeter would be 2.88 V.

Question 14.
Judge the equivalent resistance when the following are connected in parallel –
(a) 1 Ω, 10⁶ Ω, (b) 1 Ω, 10³ Ω and 10⁶ Ω
Answer:
(a) 1 ohm and 106 times ohm
R₁ = 1 ohm
R₂ = 10⁶ times = 1000000 ohm
Total resistance in parallel R = 1/R₁ + 1/R₂
= 1/1 + 1/1000000 = 1000000 + 1/1000000
= 1000001/1000000
1/R = 1/1 ohm (approx)
∴ Resistance = 1 ohm (approx)

(b) R₁ = 1 ohm
R₂ = 10³hm
R₃ = 10⁶ ohm
Total resistance in parallel

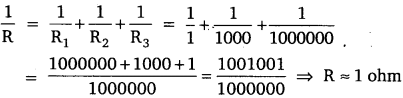
Question 15.
An electric lamp of 100 Ω, a toaster of resistance 50 Ω, and a water filter of resistance 500 Ω are connected in parallel to a 220 V source. What is the resistance of an electric iron connected to the same source that takes as much current as all the three appliances, and what is the current through it?
Answer:
Resistance of electric lamp = 100 ohm
Resistance of a toaster = 50 ohm
Resistance of a water filter = 500 ohm
Potential difference = 220 volt
Total resistance of the three appliances in parallel
1/R = 1/R₁ + 1/R₂ + 1/R₃ = 1/100 + 1/50 + 1/500
1/R = (5 + lo + 1)/500
1/R = 16/500 = 4/125
R = 125/4 = 31.25 ohm
V = I x R
220 = I x 31.25
∴ I = 7.04 amp
Hence current through the electric iron = 7.04 amp.

Question 16.
What are the advantages of connecting electrical devices in parallel with the battery instead of connecting them in series?
Answer:
Advantages of parallel connection are:
(a) In a parallel circuit, if one electric appliance stop working due to some defect, then all other appliances keep working normally.
(b) In a parallel circuit, each electrical appliance has its own switch due to which it can be turned on or off without affecting other appliances.
(c) Each electrical appliance gets the same voltage (220 V) as that of the power supply line.
(d) In parallel connection of electrical appliances, the overall resistance of the circuit is reduced due to which the current from the power supply is high.

Question 17.
How can three resistors of resistances 2Ω, 3Ω , and 6Ω be connected to give a total resistance of (a) 4 Ω, (b) 1Ω ?
Answer:
R₁ = 2 ohm
R₂ = 3 ohm
R₃ = 6 ohm
(a) When R₂ and R₃ are connected in parallel with R₁ in series we get
1/R = 1/R₂ + 1/R₃ = 1/3 + 1/6 = 1/2
Thus, R = 2 ohm
Resistance in series = R + R₁ = 2 + 2 = 4 ohm

(b) When R₁, R₂, R₃ are connected in parallel we get
1/R = 1/R₁ + 1/R₂ + 1/R₃ = 1/2 + 1/3 + 1/6 = 1 ohm.

Question 18.
What is (a) the highest, (b) the lowest total resistance that can be secured by combinations of four coils of resistance 4 Ω, 8 Ω, 12Ω, 24Ω?
Answer:
(a) The highest resistance is when the resistances are connected in series:
R₁ = 4ohm R₂ =8ohm
R₃ = 12 ohm R₄ = 24 ohm
Total resistance in series = R₁ + R₂ + R₃ + R₄
= 4 + 8 + 12 + 24 = 48 ohm
Thus, highest resistance is 48 ohm.

(b) The lowest resistance is when the resistances are connected in parallel Total resistance in parallel = 1/R₁ + 1/R₂+ 1/R₃ + 1/R₄
1/R = 1/4 + 1/8 + 1/12 + 1124 = 12/24
1/R = 1/2 ohm, R = 2 ohm
Thus, lowest resistance is 2 ohm.

Question 19.
Why does the cord of an electric heater not glow while the heating element does?
Answer:
The resistance of the cord is extremely small as compared to that of the heating element, so the heat produced in the cord is less as compared to the heating element. So the heating element begins to glow but the cord does not glow.

Question 20.
Compute the heat generated while transferring 96000 coulomb of charge in one hour through a potential difference of 50 V
Answer:
Charge = 96000 coulomb
Time = 1 hour = 3600 seconds
Potential difference = 50 V
I = Q / T
I = 96000/3600 = 80/3 amp

V = I x R
50 = 80/3 x R
Thus. R = 15 / 8 ohm
Heat = I²RT = (80/3)² x 15/8 x 3600 = 800 x 6000 = 4800000 joules.

Question 21.
An electric iron of resistance 20 Ω takes a -current of 5 A. Calculate the heat developed in 30 s.
Answer:
The resistance of the iron = 20 ohm
Current = 5 amp
Time = 30 seconds
Heat produced = I²RT = 5² x 20 x 30 = 15000 jouIes

Question 22.
What determines the rate at which energy is delivered by a current?
Answer:
Electrical power determines the rate at which the energy is delivered by a current.

Question 23.
An electric motor taΩes 5 A from a 220 V line. Determine the power of the motor and the energy consumed in 2 h.
Answer:
Current in the motor, I = 5 amp
Potential difference, V = 220 V
Time = 2 hours
Power of the motor = V x I = 220 x 5 = 1100 watt or 1.1 kW
Energy = power x time = 1.1 kW x 2 h = 2.2 kWh

In-Text Activities Solved

Activity 12.1
Answer:
To verify Ohm’s law:
Connect the circuit as shown in the figure use batters nichrome wire (XY), ammeter, key, and voltmeter.

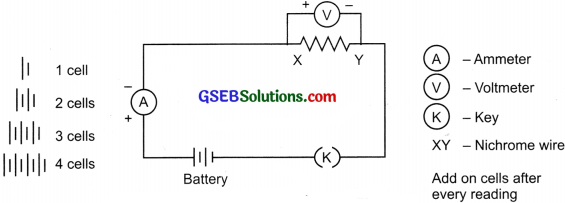
Electric circuit for studying Ohm’s law:

Conclusion: The ratio \(\frac {V}{I}\) remains constant. When V increases I also increases i.e., V= I
Graph of V vs I

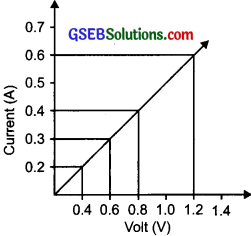
Activity 12.2
Answer:

• To observe that flow of current is different for different components. Take a nichrome wire, a torch bulb, a 10 W bulb and an ammeter (0 – 5 A range), a plug key, and some connecting wires.
• Set up the circuit by connecting four dry cells of 1.5 V each in senes with the ammeter leaving a gap XY in the circuit.
  
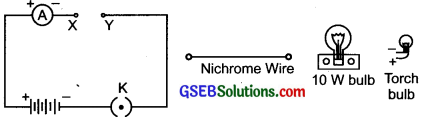
• Complete the circuit using nichrome wire in gap X Note ammeter reading.
• Now use the torch bulb in the circuit.
• Repeat the same with io w bulb.

Observation:
Ammeter reading is different for different components. This is because components may offer an easy flow of electric current or may offer resistance to the flow.

Conclusions:

• A component that offers low resistance is called a good conductor.
• A conductor which offers appreciable resistance is called a resistor.
• A component that offers a higher resistance is called a poor conductor.
• A component with very high resistance is called an insulator.

Activity 12.3
Answer:
To study the factors on which the resistance of conducting wire depends.
Method: Complete an electric circuit consisting of a cell, an ammeter, a nichrome wire of length 1, a key as shown in the figure.

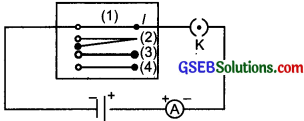
Circuit to study factors on Which the resistance of conducting wires depends.

In the given circuit, note the ammeter reading in the following cases:

•  Using nichrome wire with length l.
•  Replace the first wire and use other nichrome wire of the same thickness but double the length 2l.
• Now use a thicker wire (area of cross-section is more) of nichrome but of the same length as in the first case.
• Now replace nichrome wire with the copper wire of the same length and the same area of cross-section as in the first case.

Observation:

• The current I flows in case (1).
• The current \(\frac {1}{2}\) (half the value) flows in case (2).
• The current I increases in case (3).
• The current I decreases in case (4).

Conclusions: The resistance ‘R’ of a wire is

• directly proportional to length ‘1’ (R ∝ l).
• inversely proportional to area of cross-section ‘A’ (R ∝ \(\frac {1}{A}\)].
• directly proportional to the material of the wire.

Activity 12.4
Answer:
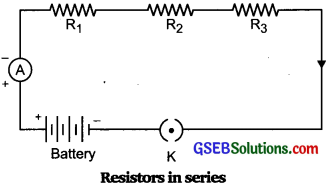
ResIstors in series: Join 3 resistors R₂, R_2, and R₃ of three different values in senes as shown in the figure. Connect them with battery an ammeter, a plug key Use resistors of value 1 Ω, 2 Ω, 3Ω etc, and a battery of 6 V for performing this activity. Note the ammeter reading. Change the position of the ammeter to anywhere in between the resistors.

Observations: The value of current I iii the ammeter is the same. Let it be placed anywhere in the circuit.
Conclusion: In a series combination of resistors, the value of current is the same in every part of the circuit.

Activity 12.5
Answer:
Take 3 resistors R₁, R₂, R₃ of different values, battery, ammeter, key, and voltmeter,
with connecting wires. Arrange the apparatus as shown in figure (a).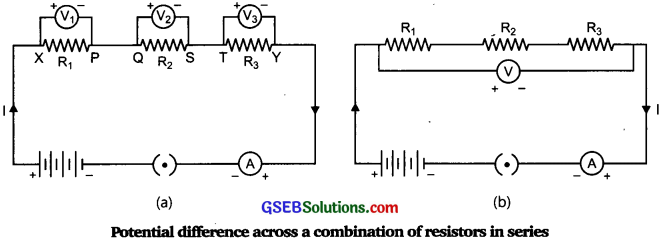
Measure potential difference by connecting the voltmeter to the individual resistors as shown in figure (a). Let it be V₁, V_2, and V₃.
Now measure the potential difference across the series combination of resistors as shown in figure (b). Let it be V

Observation:
The potential difference V in a circuit (b) is equal to potential difference V₁, V₂and V₃ in
circuit (a).
V= V₁+ V₂ + V₃

Conclusion: The total potential difference across a combination of resistors, in series, is equal to the sum of potential difference across the individual resistors.

Activity 12.6
Answer:
To study the relationship between current I and resistance R in the parallel circuits. And the relationship between potential difference V and resistance R in the parallel circuit. Take 3 resistors R₁, R₂, R₃ of different values, a battery, an ammeter, a voltmeter, and connecting wires. Arrange the set up as shown in the figure.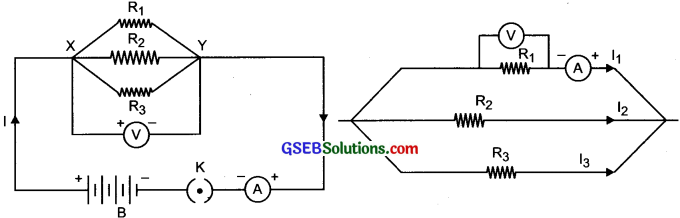

Methods:

• Note the ammeter reading when connected in series to the whole circuit. Let the
  current be I.
• Note the ammeter reading as I₁ , I ₂ and I₃ when connected to each individual resistor R₁, R_2, and R₃ respectively.
• Connect the voltmeter and take the reading when connected in parallel to the whole circuit.
• Measure the p.d. across each resistance te., R₁, R_2, and R₃ individually.

Observations:

• Ammeter showed reading I when connected in series to the circuit.
• When the ammeter reading of different resistors was added it gave the total reading equivalent to I.
  I = I₁ + I₂ + I₃
• Voltmeter reading remained constant either connected parallel to the combination of resistors or connected parallelly to each individual resistor.

Conclusion: The magnitude of current I varies and depends on the resistance R.
I ∝ \(\frac {1}{R}\) V is constant
∴ V = IR
∴ I = \(\frac {V}{R}\)
To get equivalent resistance in the circuit
I₁ = \(\frac{V}{R_{1}}\) ……….(i)
I₂ = \(\frac{V}{R_{2}}\) ……….(ii)
I₃ = \(\frac{V}{R_{3}}\) ……….(iii)

Add (i), (ii) and (iii)
I₁ + I₂ + I₃ = \(\frac{V}{R_{1}}\) + \(\frac{V}{R_{2}}\) + \(\frac{V}{R_{3}}\)
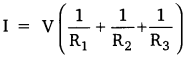or \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}\)

Gujarat Board Class 10 Science Electricity Textbook Questions and Answers

Question 1.
A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then what is the ratio R/R’?
Answer:
25 : 1

Question 2.
Which of the following terms does not represent electrical power in a circuit?
(a) I²R
(b) IR²
(c) VI
(d) V²/R
Answer:
(b) IR²

Question 3.
An electric bulb is rated 220 V and loo W. When it is operated on 110 V, the power consumed will be –
(a) 100 W
(b) 75 W
(c) 50 W
(d) 25 W
Answer:
(d) 25 W

Question 4.
Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would
be –
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1
Answer:
(c) 1 : 4

Question 5.
How is a voltmeter connected in the circuit to measure the potential difference between two points?
Answer:
It is connected in parallel.

Question 6.
A copper wire has a diameter 0.5 mm and a resistivity of 1.6 x 10^-8 Ω m. What will be the length of this wire to make its resistance 10 Ω ? How much does the resistance change if the diameter is doubled?
Answer:
Diameter = 0.5 mm = 0.0005 m
Radius r = \(\frac {0.0005}{2}\) = 0.00025 m or 0.25 x 10^-3m
Resistivity ρ = 1.6 x 10^-8Ω m
Resistance R = 10 Ω
Length l = ?
Using R = ρ \(\frac {l}{A}\) or l = \(\frac {RA}{ρ}\)

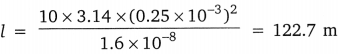
The resistance becomes one-fourth if the diameter is doubled.

Question 7.
The values of current I flowing in a circuit with a resistor for the corresponding values of potential difference V across the resistors are given below:

Plot a graph between V and I and calculate the resistance of that resistor.
Answer:

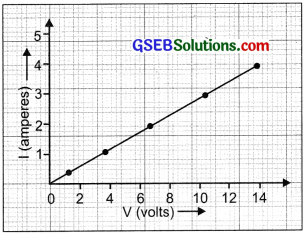
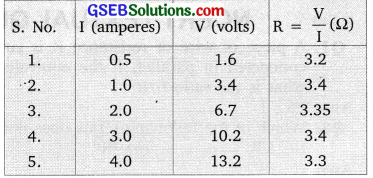
Question 8.
When a 12 V battery is connected across an unknown resistor, there is a current 2.5 mA in the circuit. Find the value of the resistance of the resistor.
Answer:
V = 12V
I = 2.5 mA = 2.5 x 10^-3A
Using, R = \(\frac {V}{I}\)
R = \(\frac{12 \mathrm{V}}{2.5 \times 10^{-3} \mathrm{A}}\) = 4800Ω = 4.8 kΩ

Question 9.
A battery of 9 V is connected in series with resistors of 0.2 Ω, 0.3 Ω, 0.4 Ω, 0.5 Ω i and 12 Ω respectively. How much current would flow through the 12 resistors?
Answer:
V = 9V
R_s = 0.2 Ω + 0.3 Ω + 0.4 Ω + 0.5 Ω + 12 Ω = 13.4 Ω
I = ?
Using, I = \(\frac {V}{R}\) = \(\frac {9V}{13.4 Ω }\) = 0.67 A
0.67A current would flow through the 12 Ω resistor.

Question 10.
How many 176 resistors (in parallel) are required to carry 5 A on a 220 V line?
Answer:
I = 5A V = 220V
Let the number of 176 Ω resistors be n.

Hence, four resistors of 176 Ω are required to carry 5 A on a 220 V line.

Question 11.
Show how you would connect three resistors each of resistance 6 so that the combination has a resistance of –
(i) 9 Ω
(ii) 4 Ω
Answer:
(i) To get 9 Ω – Connect 2 resistors of 6 Ω in the parallel and third resistor in series.

(ii) To get 4 Ω – Connect 2 resistors in series and the third in parallel to both of them

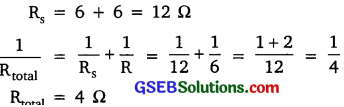
Question 12.
Several electric bulbs designed to be used on a 220 V electric supply line, are rated 10 W How many lamps can be connected in parallel to each other across the two wires of a 220 V line if the maximum allowable current is 5 A?
Answer:
P = 10W
V = 220V
I = ?
Using, I = \(\frac {V}{P}\) = \(\frac {10}{220}\) = \(\frac {1}{22}\) A
If number of bulbs connected to current of 5 A is n. Then,
\(\frac {1}{22}\) n = 5
n = 5 x 22 = 110
110 bulbs can be attached.

Question 13.
A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Answer:
(i) When used separately
I = \(\frac {V}{R}\) = \(\frac {220}{24}\) = 9.2A.

(ii) When connected in series
(R₁ = 24Ω , R₂ = 24 Ω)  R_s = R₁ + R₂ = 24 + 24 = 48 Ω
I = \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{p}}}\) = \(\frac {220}{40}\) = 4.6 A

(iii) When connected in parallel
(R₁ = 24 Ω , R₂ = 24 Ω )
\(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{24}+\frac{1}{24}=\frac{2}{24}=\frac{1}{12}\),
so, R_p = 12
I = \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{p}}}\) \(\frac {220}{12}\) = 18.3 A

Question 14.
Compare the power used in the 2 Ω resistor in each of the following circuits:
1. a 6 V battery in series with 1 Ω and 2 Ω resistors,
2. a 4 V battery in parallel with 12 Ω and 2 Ω resistors.
Answer:
1. V = 6V
R₁ = 1Ω, R₂ = 2Ω
R₁ and R₂ are in series,
R_s = R₁ + R₂ = 1 + 2 = 3Ω
Current flowing through the circuit, I = \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{s}}}\)
So, I = \(\frac {6}{3}\) = 2A

Power = I² R_s = (2)² x 3 = 12 W
∴ 12 W power is used in the 2Ω resistor in this circuit.

2. R₁ =12 Ω
R₂ = 2 Ω Parallel V = 4V p₂ = ?

∴ I₁ through 2 Ω =\(\frac {4V}{2Ω}\) = 2 A
P₂ = I² R_s = (2)² = 8W

Question 15.
Two lamps, one rated loo W at 220 V, and the other rated 60 W at 220 V, are connected in parallel to the electric mains supply. What current is drawn from the line if the supply voltage is 220 V?
Answer:
P₁ = 100W
P₂ = 60W
p = p₁ + p₂ = 160 W
V = 220V
I = ?
Using P = IV or I = \(\frac {P}{V}\) = \(\frac {160}{220}\) = 0.73 A

Question 16.
Which uses more energy; a 250 W TV set in 1 hr, or a 1200 W toaster in 10 minutes?
Answer:
250 W 1V set in an hour.

Question 17.
An electric heater of resistance 8 Ω draws 15 A from the service mains for 2 hours. Calculate the rate at which heat is developed in the heater.
Answer:
P = I²R = (15)² x 8 = 1800 Watt.

Question 18.
Explain the following:
(a) Why the tungsten is used almost exclusively for the filament of electric lamps?
Answer:

• It has a special property that it glows on heating.
• It has a high melting point.
• It does not react with the gases present in the air and does not get oxidized.
• It has a low resistance.

(b) Why are the conductors of electric heating devices, such as bread-toasters and electric irons, made up of alloys rather than pure metal?
Answer:

• They offer higher resistance than pure metals, thus heating better.
• They have a high melting point.
• They do not oxidize.

(c) Why is the series arrangement not used for domestic circuits?
Answer:
If any appliance is at fault, then the current is not able to flow through. Different appliances have different current requirements, but in series, the current is the same. This can cause a power surge, thus damaging the appliances. Very long wires in domestic series circuits offer unusually high resistance, which is unwanted.

(d) How does the resistance of a wire vary with its area of cross-section?
Answer:
The relation between the resistance of a wire and its area of the cross-section can be defined as:
R is inversely proportional to the area of cross-section R ∝ (R ∝ \(\frac {1}{A}\))

(e) Why copper and aluminium wires are usually employed for electricity transmission?
Answer:

• Copper and aluminum are much more easily and cheaply available than other metals.
• They offer low resistance and do not get heated.
• They can be easily made into wires due to high malleability

Gujarat Board Class 10 Science Electricity Additional Important Questions and Answers

Very Short Answer Type Questions

Question 1.
What is S.I. unit of charge?
Answer:
Coulomb.

Question 2.
Give the S.I. unit of electric current.
Answer:
Ampere (A).

Question 3.
What is S.I. unit of electric potential?
Answer:
Volt

Question 4.
Give the unit of electric resistance.
Answer:
Ohm (Ω)

Question 5.
How is resistance, volt, and current (I) related?
Answer:
R = \(\frac {V}{I}\),V = IR

Question 6.
How is 1 ohm related to ampere and volt?
Answer:

Question 7.
What constitutes the current?
Answer:
The flow of free electrons constitutes the current.

Question 8.
When the given resistances are connected in series, which physical quantity does not change.
Answer:
Current.

Question 9.
What is an ammeter?
Answer:
A measuring instrument used to measure electric current.

Question 10.
What is a voltmeter?
Answer:
A measuring instrument used to measure the potential difference between two points in an electric circuit.

Question 11.
Give the unit of power.
Answer:
Watt.

Question 12.
How is power related to current and voltage?
Answer:
Power = V x I
Power (P) = Potential difference (V) x Current (I)

Question 13.
How are ammeter and voltmeter connected in a circuit?
Answer:
An ammeter is connected in series and voltmeter is connected in parallel.

Question 14.
What happens to the resistance when the length of the conductor is doubled without affecting the thicΩness of the conductor?
Answer:
Resistance is doubled because it is directly proportional to length.

Question 15.
How many electrons are there in 1 C of charge?
Answer:
There are 6.25 X 10¹⁸ electrons in 1 C of charge.

Question 16.
What is the S.l. unit of resistivity?
Answer:
Ohm meter.

Question 17.
Find the total resistance in the given circuit.

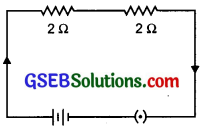
Answer:
Two resistances are connected in series, the effective resistance is 2 + 2 = 4 Ω

Question 18.
The combined resistance in the given circuit is 5 Ω What is the value of R?

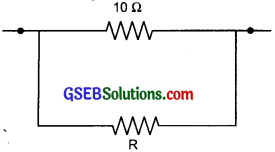
Answer:
In parallel \(\frac{1}{\mathrm{R}_{1}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}\)

hence \(\frac{1}{5}=\frac{1}{10}+\frac{1}{\mathrm{R}_{2}}\)
∴ \(\frac{1}{\mathrm{R}_{2}}=\frac{1}{5}-\frac{1}{10}\)
∴ R₂ = 10 Ω

Question 19.
What is the effective resistance in the given circuit?
Answer:
The sum of resistances of different components of the circuit.

Question 20.
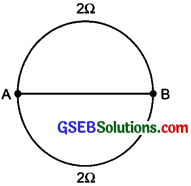
A wire of resistance 4 Ω is bent in the form of a closed circle. What is the resistance between the two points at the ends of any diameter of the circle?
Answer:
Between two points A and B, the resistance is divided into two semicircular parts each having resistance 2 Ω Being in parallel connection, total resistance will be
\(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}\)
∴ \(\frac{1}{R_{p}}=\frac{1}{2}+\frac{1}{2}\)
∴ \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{2}{2} \mathrm{R}_{\mathrm{p}}\) = 1 Ω

Short Answer Type Questions

Question 1.
Give differences between conductors and insulators.
Answer:
Conductor:

• Materials that allow electricity to pass through them.
• These materials have loosely bounded free electrons.
• E.g., metals and graphite (Non-metal).

insulators:

• I Materials that do not allow electricity to pass through them.
• These materials do not have loosely bounded free electrons.
• E.g., non-metals, rubber, plastic etc.

Question 2.
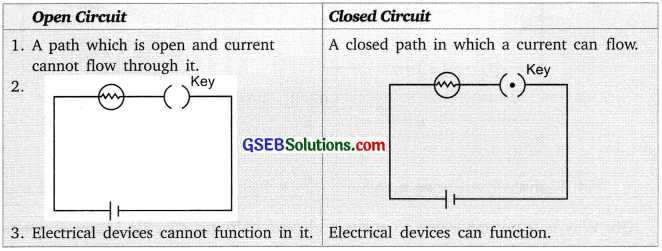
Give two points of difference between open circuit and closed circuit.
Answer:

Question 3.
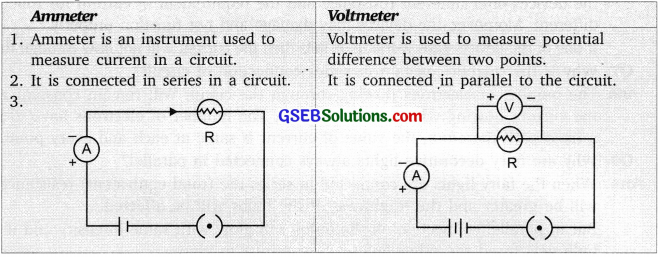
Give two points of difference between ammeter and voltmeter.
Answer:

Question 4.
Give two points of difference between resistance and resistivity
Answer:

• it is the property of a conductor to resist the flow of charges through it.
• Its unit is ohm (Ω).
• Resistance depends on length, cross sectional area of the wire, and material of wire and temperature.
  R = \(\frac {1}{A}\) (R = T)

Resistivity:

• it is the resistance per unit length of a umt cross-section area of the material.
• Its unit is ohm meter (Ω m).
• Resistivity is the constant value for a material that depends on its temperature. P ∝ T
• Resistivity increases with a rise in the temperature of metals and alloys.

Question 5.
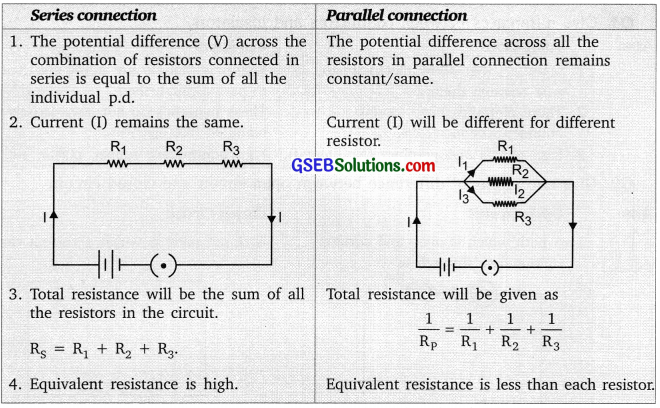
Give the differences between series and parallel connections of resistors.
Answer:

Question 6.
Why is it not advisable to connect electric bulbs and electric heater in series?
Answer:
It is not advisable to connect electric bulbs and electric heater in series because both the devices offer different resistance and the requirement of current for functioning is different. Moreover, the devices may damage and not function properly. if one of the devices stops working or fails then the current will not flow through the circuit.

Question 7.
Why is the current constant in the series connection of the circuit?
Answer:
The number of electrons flowing through the circuit will remain constant therefore the current flowing will also be constant. The number of electrons has to travel in a fixed path therefore, the value of current is the same at each and every point.

Question 8.
Why are fairy decorative lights always connected in parallel?
Answer:
When the fairy lights are connected in series the (total equivalent) resistance offered will be greater and the brightness of the bulbs will be affected. But in parallel connection all the bulbs will glow with the same intensity and if anyone bulbs gets fused the other bulbs will continue to glow.

Question 9.
What is a purely resistive electric circuit?
Answer:
The purely resistive electric circuit is the one in which the resistor is connected to the battery such that the source energy gets dissipated entirely in the form of heat.

Question 10.
Give the difference in unit of electric energy and commercial unit of electric energy
Answer:
The unit for electric energy is watt-second i.e., Joules. For the commercial unit of electric energy we use kilowatt-hour.

Question 11.
Define one-watt hour and one Ωilowatt hour.
Answer:
One watt-hour is the energy consumed when 1 watt of power is used for 1 hour. One Kilowatt-hour is the energy consumed when 1 Ωilo watt (1000 watts) of power is used for 1 hour.

Question 12.
Give two disadvantages of the heating effect of current.
Answer:
The current when flows through any conductor produce a heating effect. This heat produced cannot be utilized at all the places, rather it damages the circuits causing high temperatures and the melting of other materials can cause damage. To keep the temperature low and cool the circuit, fans are set up e.g. In computers fans are inbuilt to keep the components cool.

Question 13.
Give two advantages of the heating effect of electric current.
Answer:
The heating effect of electric current has many uses as it is used in electric toasters, room heaters, here the electric energy is deliberately made to get converted into heat energy and this heat energy is used further in many devices.

Question 14.
Why do we prefer tungsten metal in electrical bulbs and why not some other metal of the same resistivity can be used?
Answer:
Tungsten metal has very peculiar properties due to which it is used in the electric bulb, these properties are not seen in other metals with the same resistivity
The properties are:
1. It emits light and glows when it gets heated.
2. It does not melt at high temperatures (M.R 3380°C).

Question 15.
Name the factors on which Joule’s law of heating depends.
Answer:
Joule’s law of heating depends on the following:
H ∝ I² RT

• the heat produced in a resistor is directly proportional to the square of current for a given resistance.2.
  
• the heat produced in a resistor is directly proportional to the resistance for a given current and
• the heat prodùced in a resistor is directly proportional to the time for which the current flows through the resistor.

Question 16.
What is the electric current? What is the conventional direction of electric current? Why was this direction taken to represent the flow of electric current?
Answer:
Electric current is the rate of the flow of electrons through a particular area in unit time. It is the electrons that flow. Conventionally the direction of an electric circuit in a circuit is taken from the positive terminal towards the negative terminal because the electrons were not known when the phenomenon of electricity was observed. The current was considered to be the flow of positive charges and the direction of flow of positive charges was taken to be the direction of electric current.

Question 17.
What do the following symbols represent in the electric circuit?
\(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}\) = \(\frac{1}{5}+\frac{1}{10}+\frac{1}{30}=\frac{1}{3}\)
Answer:
The symbols used in the circuit diagram are named as:

Question 18.
What is the potential difference? Explain and give its unit with a definition.

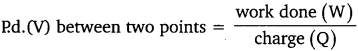
V = \(\frac {W}{Q}\)
The S.L. unit of electric potential difference is volt (V).
1 volt is the potential difference between two points in a current-carrying conductor when 1 Joule of work is done in moving a charge of I coulomb from one point to another.

1 V = \(\frac {1J}{1C}\)

Question 19.
How much work is done in moving a charge of 4 C across two points having a potential difference of 12 V ? Calculate the number of electrons flowing in it.
Answer.
Q = 4 C
V = 12 V
W = ?
W = VQ = 12 V X 4 C
W = 48 J
1 C = 6.25 X 10¹⁸ eletrons
4 C = 6.25 X 10¹⁸ x 4 = 25.00 x 10¹⁸ = 2.5 x 10¹⁹ eletrons

Question 20.
A circuit diagram is given below.

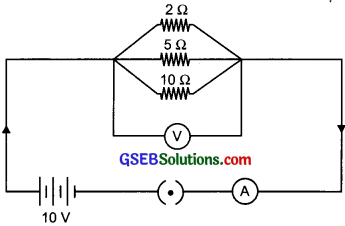
Calculate:
(a) Current through each resistor.
(b) The total current in the circuit.
(c) The total effective resistance of the circuit.
Solution:
R₁ = 2 Ω V = 10 V
R₂ = 5 Ω
R₃ = 1 Ω
Answer:
(a) Current through each resistor
I₁ = \(\frac{V}{R_{1}}\) = \(\frac {10}{2}\) = 5 A
I₂ = \(\frac{V}{R_{2}}\) = \(\frac {10}{5}\) = 2 A
I₃ = \(\frac{V}{R_{3}}\) = \(\frac {10}{10}\) = 1 A
I = I₁ + I₂ + I₃ = 5 + 2 + 1 = 8 A
(b) Total current
(c) Total resistance

As resistance is in parallel
\(\frac{1}{\mathrm{R}_{\mathrm{P}}}\) = \(\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}\) = \(\frac{1}{2}+\frac{1}{5}+\frac{1}{10}\) = \(\frac {5 + 2 + 1}{10}\) = \(\frac {8}{10}\)
R_p = \(\frac {10}{8}\) = 1.25 ohm

Question 21.
You are given 3 resistors each of 3 ohm and you are asked to get all possible values of resistance when you connect them in different combinations. How many values of resistance can you get?
Answer:
(i) When connected in series

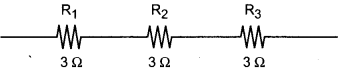
(ii) When we connect in parallel

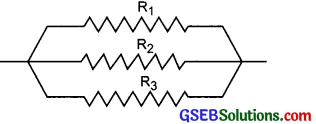
(iii)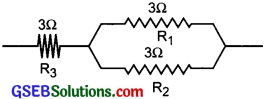
\(\frac{1}{\mathrm{R}_{\mathrm{P}}}\) = \(\frac{1}{R_{1}}+\frac{1}{R_{2}}\)
\(\frac{1}{\mathrm{R}_{\mathrm{P}}}\) = \(\frac{1}{3}+\frac{1}{3}=\frac{2}{3}\)
∴ R_p = \(\frac {3}{2}\) = 1.5 Ω
R = R_p + R₃ = 1.5 + 3 = 4.5 Ω

(iv)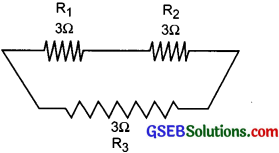
R_s = R₁ + R₂ = 3 + 3 = 6Ω
\(\frac{1}{\mathrm{R}_{\mathrm{P}}}\) = \(\frac{1}{\mathrm{R}_{\mathrm{S}}}+\frac{1}{\mathrm{R}_{3}}\) = \(\frac {1}{6}\) + \(\frac {1}{3}\) = \(\frac {1 + 2}{6}\) = \(\frac {3}{2}\) = \(\frac {1}{2}\)
R_p = 2Ω

Question 22.
A battery of 10 V is connected in a circuit with 3 Ω, 4 Ω, 6Ω resistors connected in series. How much current will flow through 6 Ω resistor?

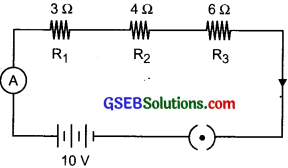
Answer:
The total resistance in series
R_s = R₁ + R₂ + R₃ = 3 + 4 + 6
R_s = 13 Ω
V = 10V
I = ?
I = \(\frac {V}{ R}\) = \(\frac {10}{13 }\)
I = 0.77 A
The current flowing through 6Ω resistor is i.e. 0.77 A. In series connection same current flows through each resistor.

Question 23.
Two electric bulbs are rated 60 W, 220 V, and 20 W, 220 V, are connected in parallel to a 220 V supply. Calculate the total electric current in the circuit.
Answer:
Given
Bulb 1 : P = 60 W
V = 220V
1 = ?
p = VI
∴ I = \(\frac {P}{V}\) = \(\frac {60}{220}\) = 0.27 A

Bulb 2 : P = 20 W
V = 220 V
1 = ?
p = VI
∴ I = \(\frac {P}{V}\) = \(\frac {20}{220}\) = 0.09 A
Total current I = I₁ + I₂ = 0.27 + 0.09
I = 0.36 Ampere

Question 24.
An electric lamp draws a current of 0.3 ampere and is used for 6 hours every day for a month (30 days). Calculate the amount of charge that flows through the circuit every day and for a month.
Answer:
I = 0.3A
t = 6 hours = 6 x 60 x 60 sec.
charge,Q = It
perday = 0.3 x 6 x 60 x 60 = 6480C
Charge flowing for a month = 6480 X 30 = 194400 C

Queastion 25.
Describe an activity to prove that resistance of a wire depends on its length, cross-sectional area, and material of the wire.
Answer:
Complete an electric circuit consisting of a cell, an ammeter, a nichrome wire of length l [say, marked (1)], and a plug key, as shown in the figure.

 

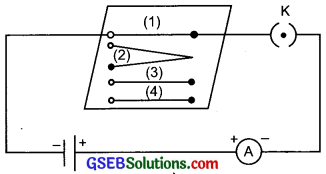
• Electric circuit to study the factors on which the resistance of coñducting wires depends.
• Now, plug the key. Note the current in the ammeter.
• Replace the nichrome wire by another nichrome wire of same thickness but twice the length, that is 2l [marked (2) in the figure].
• Note the ammeter reading.
• Now replace the wire by a thicker nichrome wire, of the same length l [marked (3)]. The thicker wire has a larger cross-sectional area. Again note down the current through the circuit.
• Instead of taking a nichrome wire, connect a copper wire [marked (4) in the figure] in the circuit. Let the wire be of the same length and same area of cross-section as
• that of the first nichrome wire [marked (1)]. Note the value of the current.
• Notice the difference in the current in all cases.

Observations:

• It is observed that the ammeter reading decreases to one-half when the length of the wire is doubled.
• Ammeter reading increased when a thicker wire of the same material and of the same length is used in the circuit.
• A change in ammeter reading is observed when a wire of different material of the same length and the same area of cross-section is used.

Conclusion:
The resistance of the conductor depends on:
length of the wire, R ∝ I
area of cross-section of the wire, R ∝ \(\frac {1}{A}\)
the nature of the material of the wire.

So,
R = \(\frac {l}{A}\)
∴ R = ρ \(\frac {l}{A}\)

Question 26.
what is the heating effect of electric current? Find the expression for calculating ‘Heat’.
Answer:
When current passes through the wire conductor, the temperature of the conductor increases and heat is emitted. This is called the heating effect of electric current. Consider a current I flowing through a resistor of a resistance R. Let the potential difference across it be V Let ‘t’ be the time during which a charge Q flows across. The work done in moving charge Q from one point to another through a potential difference V is VQ Therefore, the source must supply energy which is equal to VQ
in time t.
Hence the power P = \(\frac {VQ}{t}\) ………..(1)
I = \(\frac {Q}{t}\) ………..(2)
∴ P = VI ……..(3)
The energy supplied in time ‘t’ = P x t ……….(4)
P x t = VIt From (3) and (4) equation
The energy supplied gets utilized in the form of heat.
H = VIt
Ohm’s law: V = IR
On substituting V in H = VIt
We get H = IR x It
H = I²Rt.

Long Answer Type Questions

Question 1.
What is the resistance of the conductors? Name two metals that offer very high resistance. Name the factors on which the resistance of the conductor depends.
Answer:
Resistance: It is the property of a conductor to resist the flow of charges through it. Its S.J. unit is ohm Ω Two metals with low resistance are silver and copper. Two metals that offer high resistance are mercury and manganese. Factors on which resistance of a conductor depend are: length of the conductor area of cross-section and material.

Question 2.
State Ohm’s law. Draw a graph between voltage and current for a metallic conductor. Draw a circuit diagram of a circuit that consists of battery ammeter, voltmeter, resistor, rheostat, and a Ωey.
Answer:
The potential difference V across the ends of a given metallic wire in an electric circuit is directly proportional to the current flowing through it, its temperature should remain constant. This is called Ohm’s law.
V ∝ I
V = IR

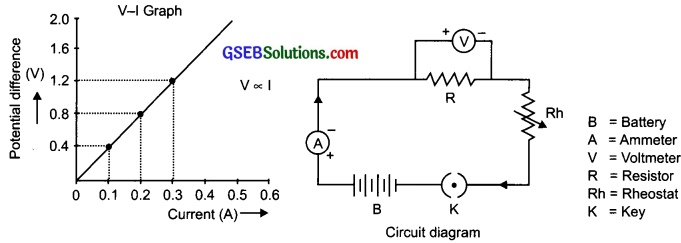
Question 3.
(a) A torch bulb is rated 2.5 V and 750 mA. Calculate –
1. its power
2. its resistance,
3. the energy consumed if in this bulb is lighted for 4 hours.
(b) Two identical resistors, each of resistance 2 Ohm, are connected in the torch
1. in series and
2. in parallel, to a battery of 12 volts. Calculate the ratio of power consumed in two cases.
Answer:
(a )V = 2.5V P = ? Energy E = ? I = 750 mA = 0.75 A. R = ? t = 4 hours
1. P = VI ∴ P = 2.5 x 0.75 = 1.875W
2. R = \(\frac {V}{I}\) ∴R = \(\frac {2.5}{0.75}\) = 3.33 Ω
3. E = Pt ∴E = 1.8 W x 4 = 7.2 Wh

(b) R₁ = R₂ = 2Ω p = ? \(\frac{P_{1}}{P_{2}}\) = ?
V = 12V p₂ = ?
Series
1. R = R₁ + R₂ = 2 + 2 = 4Ω
I = \(\frac {V}{R}\) = \(\frac {12}{4}\) = 3A
∴P₁ = VI = 12 x 3 = 36W

Parallel
2. \(\frac {1}{R}\) = \(\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}=\frac{1}{2}+\frac{1}{2}\) = 1Ω
I = \(\frac {V}{R}\) = \(\frac {12}{1}\) =12A
∴ P₂ = Vl = 12 x 12 = 144W
Hence, \(\frac{P_{1}}{P_{2}}\) = \(\frac {36}{144}\) = \(\frac {1}{4}\) = 1 : 4

Question 4.
1. Three resistors are connected as shown in the circuit diagram. Through resistor 5 ohm, a current of 2 amperes is flowing.
(a) What is the current through the other two resistors?
(b) What is the p.d. across AB?
(c) What is the total resistance?
2. Can you change the setup and arrange the resistance in a manner to get the least resistance?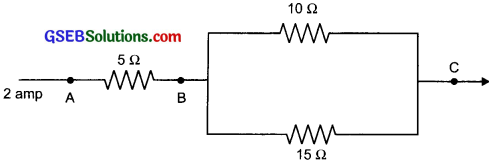
Answer:
1. (a) In Parallel I = \(\frac {V}{R}\) or, 2 x 5 = V = 10 V
For 10 Ω 2 resistance I = \(\frac {V}{R}\) = \(\frac {10}{10}\) = 1 A
For 15 Ω resistance I = \(\frac {V}{R}\) = \(\frac {10}{15}\) = 0.7 A

(b) I = \(\frac {V}{R}\)
or; 2 = \(\frac {V}{5}\)
or V = 10 V

(c) Resistance in Parallel
\(\frac {1}{R}\) = \(\frac{1}{10}+\frac{1}{15}=\frac{5}{30}=\frac{1}{6}\)

So, R = 6Ω
So, Total resistance across AC
= 5 + 6 = 11Ω

2.
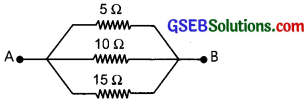
If we connect all the resistance in parallel we will get the least total resistance.

Question 5.
(a) Why is tungsten metal not used in fuse wire but is used in the bulb?
(b) Give one application of the nichrome wire and state the reason for its use.
Answer:
(a) tungsten metal has specific properties of high melting point 3380°C, it emits light when it gets heated and does not get oxidized. Hence it is used in the electric bulbs to emit light. But in case of fuse wire – fuse is a safety device that protects the circuit
from electrical hazards. If tungsten is used, its melting point is high then a large amount of current will flow through the wire and other electrical appliances may get damaged. Hence it is not advisable to be used in fuse wire.

(b) Nichrome wire is an alloy made up of ficΩle and chromium and offers very high resistance which allows converting the electrical energy into heat energy. Hence it is used as a heating device.

Question 6.
(a) Why is a series arrangement not used for domestic circuits?
(b) Explain why fuse wire is always connected in a series arrangement.
(c) Why are copper and aluminum wires usually employed for electricity transmission?
Answer:
(a) Series arrangement is not used for domestic circuits because the same current will flow through all the appliances. The equivalent resistance (i.e. total resistance) will get added and hence the current drawn by the circuit will be less.

(b) Fuse wire is always connected in series in a circuit as it has to checΩ the flow of current through the circuit and prevent the extra flow of current through it.

(c) Copper and aluminum are usually employed for electricity transmission because they have very low resistivity and are very good conductors of electricity. Both metals are cheap and ductile.

Questions On Higher Order Thinking Skills (Hots)

Question 1.
Why don’t birds sitting on live wire get an electric shock?
Answer:
Birds when sit on the live wire just add to the circuit, it does not get shocked because the current is not flowing out of its body to any other material.

Question 2.
Why is the tungsten metal more coiled in the bulb and not installed in a straight parallel wire form?
Answer:
The coiled wire of tungsten increases the surface area of the wire in very less space so as to emit more light and help in glowing with more intensity

Question 3.
Name two solids and two liquid that are good conductors of electricity
Answer:
Two solids that allow electricity to pass through them are copper and aluminum.
Two liquids are – Water + dii. H₂SO₄ and Water + Sodium chloride salt.

Practical Based Questions (Solved)

Question 1.
A student wishes to verify Ohm’s law in the lab. Make a list of the materials required for this experiment.
Answer:
Materials required: Ammeter, voltmeter, connecting wires, resistor, a key, and a battery

Question 2.
On collecting the readings of the Ohm’s law experiment, the student wants to present it and analyze it, how should this be done?
Answer:
The student should make an observation table to write his observation and the data collected.

The student should then plot a graph of V and I keeping values of V to be plotted on X-axis and the current I on the Y-axis.

Question 3.
Before using devices like ammeter and voltmeter for any experiment what are the two points to be kept in mind for consideration?
Answer:
Both the ammeter and voltmeter may have some error and hence the error should be recorded and the least count should be studied for measuring the correct values.

Question 4.
For finding the total resistance, when 3 resistors are connected in the series show how the voltmeter should be connected.
Answer:

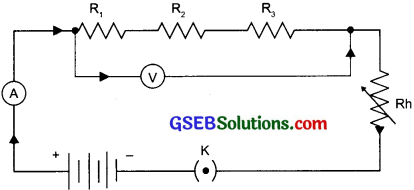
Question 5.
On connecting the 2 resistors, voltmeter, ammeter, and key correctly to the battery the ammeter did not show any readings, what could be the errors and how can it be rectified?
Answer:
The connections of the ammeter may be loose, reconnect the wires to the terminals of the ammeter. The ammeter may be of different range or value hence choose the ammeter range appropriately.

Question 6.
To calculate the resultant resistance of two resistors when connected in parallel, show how the connection in the circuit should be made?
Answer:

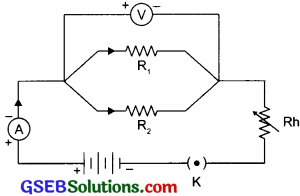
Question 7.
A student records the following four readings of the ammeter for the same circuit: 0.24A, 0.3A, 0.25A, 0.23A Which reading should he omit if he has to keep only three readings for the record and justify your choice?
Answer:
The student should not consider the second reading that is 0.3A as this one is not closer to the other readings. The concurrent readings are always picked up for better results.

Question 8.
When you connect 3 resistors of the same value in series and then in parallel in which case the current drawn in the circuit will be more and why?
Answer:
When the 3 resistors are connected in parallel the current drawn will be less than in the other case when they are connected in series. This is because the current can flow through three different pathways in the parallel connections hence varies and depends
on the value of the resistor.

Question 9.
The graph of V – I is a straight line. Mention three conclusions one can draw from this graph.
Answer:
The V-I graph with a straight line shows that the Voltage V is directly proportional to the Current I. The slope of V – I give resistance R which is always constant for that graph. The value of resistance R can be calculated.