GSEB Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.3

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.3 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.3

Solve each of the following equations:
1. x² + 3 = 0
2. 2x² + x + 1 = 0
3. x² + 3x + 9 = 0
4. – x² + x – 2 = 0
5. x² + 3x + 5 = 0
6. x² – x + 2 = 0
7. \(\sqrt{2}\)x² + x + \(\sqrt{2}\) = 0
8. \(\sqrt{3}\)x² – \(\sqrt{2}\)x + 3\(\sqrt{3}\) = 0
9. x² + x + \(\frac{1}{\sqrt{2}}\) = 0
10. x² + \(\frac{x}{\sqrt{2}}\) + 1 = 0.
Solutions to questions 1 to 10:
1. x² + 3 = 0 ⇒ x² = – 3
∴ x = ±\(\sqrt{- 3}\) = ±\(\sqrt{3i}\).

2. 2x² + x + 1 = 0.
Comparing with ax² + bx + c = 0,
a = 2, b = 1, c = 1.
∴ b² – 4ac = 1² – 4.2.1 = 1 – 8 = – 7
∴ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) = \(\frac{-1 \pm \sqrt{-7}}{2.2}\) = \(\frac{-1 \pm \sqrt{7} i}{4}\).

3. x² + 3x + 9 = 0
∴ a = 1, b = 3, c = 9
∴ b² – 4ac = 32 – 4.1.9
= 9 – 36
= – 27.

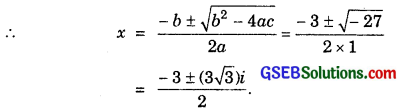
4. – x² + x – 2 = 0 or x² – x + 2 = 0.
Here, a = 1, b = – 1, c = 2.
∴ b² – 4ac = (- 1)² – 4.1.2
= 1 – 8 = – 7.
∴ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) = \(\frac{-1 \pm \sqrt{-7}}{2.1}\) = \(\frac{-1 \pm \sqrt{7} i}{2}\).

5. x² + 3x + 5 = 0
∴ a = 1, b = 3, c = 5.
∴ b² – 4ac = 9 – 4.1.5 = 9 – 20 = – 11.

6. x² – x + 2 = 0
∴ a = 1, b = – 1, c = 2.
∴ b² – 4ac = (- 1)² – 4.1.2 = 1 – 8 = – 7.
∴ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) = \(\frac{-1 \pm \sqrt{-7}}{2.1}\) = \(\frac{-1 \pm \sqrt{7} i}{2}\).

7. \(\sqrt{2}\)x² + x + \(\sqrt{2}\) = 0
∴ a = \(\sqrt{2}\), b = 1, c = \(\sqrt{2}\).
∴ b² – 4ac = 1² – 4(\(\sqrt{2}\).\(\sqrt{2}\)) = 1 – 8 = – 7.
∴ \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) = \(\frac{-1 \pm \sqrt{-7}}{2 \cdot \sqrt{2}}\) = \(\frac{-1 \pm \sqrt{-7} i}{2 \sqrt{2}}\).

8. \(\sqrt{3}\)x² – \(\sqrt{2}\)x + 3\(\sqrt{3}\) = 0
∴ a = \(\sqrt{3}\), b = – \(\sqrt{2}\), c = 3\(\sqrt{3}\).
∴ b² – 4ac = (- \(\sqrt{2}\))² – 4.\(\sqrt{3}\).3\(\sqrt{3}\) = 2 – 36 = – 34.

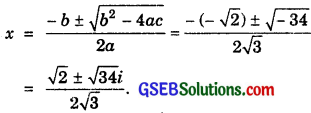
9. x² + x + \(\frac{1}{\sqrt{2}}\) = 0, Multiplying by \(\sqrt{2}\), we get
\(\sqrt{2x}\) + \(\sqrt{2x}\) + 1 = 0.
∴ a = \(\sqrt{2}\), b = \(\sqrt{2}\), c = 1.
∴ b² – 4ac = (\(\sqrt{2}\))² – 4.\(\sqrt{2}\).1 = 2 – 4\(\sqrt{2}\).

10. x² + \(\frac{x}{\sqrt{2}}\) + 1 = 0
Multiplying by \(\sqrt{2}\), we get
\(\sqrt{2}\)x² + x + \(\sqrt{2}\) = 0.
∴ a = \(\sqrt{2}\), b = 1, c = \(\sqrt{2}\)
∴ b² – 4ac = 1² – 4\(\sqrt{2}\).\(\sqrt{2}\) = 1 – 8 = – 7.
∴ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) = \(\frac{-1 \pm \sqrt{-7}}{2 \sqrt{2}}\) = \(\frac{-1 \pm \sqrt{7} i}{2 \sqrt{2}}\).