GSEB Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.1

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 4 Measures of Dispersion Ex 4.1 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.1

Question 1.
The following data refer to the heights in cms. of 10 students of a class. Find range and coefficient of range of height of the students.

Answer:
Here, x_H = 185 cm; x_L=145cm

Range of height:
R = x_H – x_L
= 185 – 145
= 40 cm
Coefficient of range = \(\frac{x_{\mathrm{H}}-x_{\mathrm{L}}}{x_{\mathrm{H}}+x_{\mathrm{L}}}\)
= \(\frac{185-145}{185+145}\)
= \(\frac{40}{330}\)
= 0.12

Question 2.
A bus company has 77 buses for travelling in the city. The information of number of passengers in bus on a particular day at a particular time is given below. Find the range and coefficient of range of number of passengers.

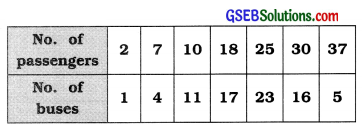
Answer:
Here. X_H = Maximum passengers travelling in a bus = 37
X_L = Minimum passengers travelling in a bus = 2

Range of number of passengers:
R = x_H – x_L
= 37 – 2
= 35 Passengers

Coefficient of range = \(\frac{\mathrm{R}}{x_{\mathrm{H}}+x_{\mathrm{L}}}\)
= \(\frac{35}{37+2}\)
= \(\frac{35}{39}\)
= 0.90

Question 3.
Using the following frequency distribution of marks of students of a school, find range and relative range of the marks:

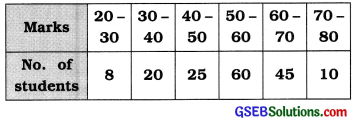
Answer:
Here, x_H = Upper limit of the last class 70 – 80 = 80 marks
x_L = Lower limit of the initial class 20 – 30 = 20 marks

Range of marks of students :
R = x_H – x_L
= 80 – 20 = 60 marks

Relative range of marks:
Relative range = \(\frac{\mathrm{R}}{x_{\mathrm{H}}+x_{\mathrm{L}}}\)
= \(\frac{60}{80+20}\)
= \(\frac{60}{100}\)
= 0.60

Question 4.
The frequency distribution of daily income , (in thousand of 80 shops of an area is as follows. Find the absolute and the relative measure of range of daily income from it.

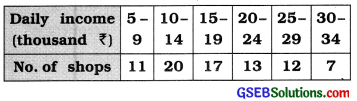
Answer:
Here, x_H = Upper limit of the last class 30 – 34 = ₹ 34
x_L = Lower limit of the initial class 5-9 = ₹ 5
Absolute measure of range of age:
R = x_H – x_L
= 34 – 5 = ₹ 29 thousand

Relative measure of range of age:
Coefficient of range = \(\frac{x_{\mathrm{H}}-x_{\mathrm{L}}}{x_{\mathrm{H}}+x_{\mathrm{L}}}=\frac{\mathrm{R}}{x_{\mathrm{H}}+x_{\mathrm{L}}}\)
= \(\frac{29}{34+5}\)
= \(\frac{29}{39}\)
= 0.74