Gujarat Board Statistics Class 11 GSEB Solutions Chapter 4 Measures of Dispersion Ex 4.4 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.4
Question 1.
The marks obtained by 9 students in a test of 100 marks in Mathematics are given below:
64, 63, 72, 65, 68, 69, 66, 67, 69
Find the standard deviation of marks obtained by the students.
Answer:
Here n = 9
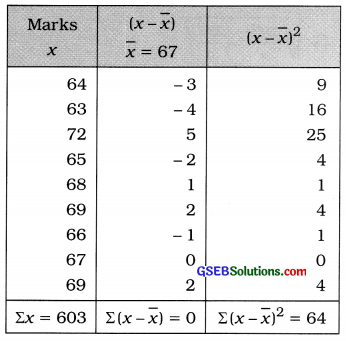
Mean:
x̄ = \(\frac{\Sigma x}{n}=\frac{603}{9}\) = 67 marks
Standard deviation of marks:
s = \(\sqrt{\frac{\Sigma(x-\bar{x})^{2}}{n}}\)
= \(\sqrt{\frac{64}{9}}\)
= \(\sqrt{7.111}\)
= 2.67 marks
![]()
Question 2.
The numbers of cars coming for service in five service stations of a company on a particular day are 7, 3, 11, 8, 9. Calculate the standard deviation of number of cars coming at the service station.
Answer:
Here, n = 5

Mean:
x̄ = \(\frac{\Sigma x}{n}\)
= \(\frac{38}{5}\)
= 7.6 Cars
Standard deviation of number of cars for service:
S = \(\sqrt{\frac{\Sigma(x-\bar{x})^{2}}{n}}\)
= \(\sqrt{\frac{35.20}{5}}\)
= \(\sqrt{7.04}\)
= 2.65 cars
Question 3.
The following frequency distribution represents the amounts of deposits and the number of depositors in a bank. Find the coefficient of standard deviation of the deposits.

Answer:
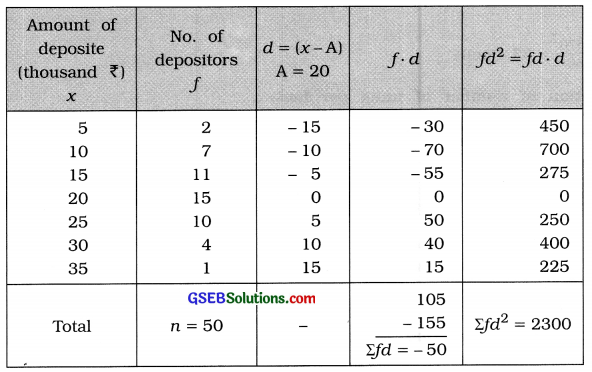
Mean:
x̄ = A + \(\frac{\Sigma f d}{n}\)
= 20 – \(\frac{50}{50}\)
= 20 – 1
= ₹ 19 thousand
Standard deviation of amount of deposites:
s = \(\sqrt{\frac{\Sigma f d^{2}}{n}-\left(\frac{\Sigma f d}{n}\right)^{2}}\)
= \(\sqrt{\frac{2300}{50}-\left(\frac{-50}{50}\right)^{2}}\)
= \(\sqrt{46-(-1)^{2}}\)
= \(\sqrt{46-1}=\sqrt{45}\) = ₹ 6.71 thousand
Coefficient of standard deviation
= \(\frac{s}{\bar{x}}=\frac{6.71}{19}\) = 0.35
![]()
Question 4.
The information of profits (in lakh ?) of 50 firms in the last year is given below. Find the standard deviation of the profit of the firms.

Answer:
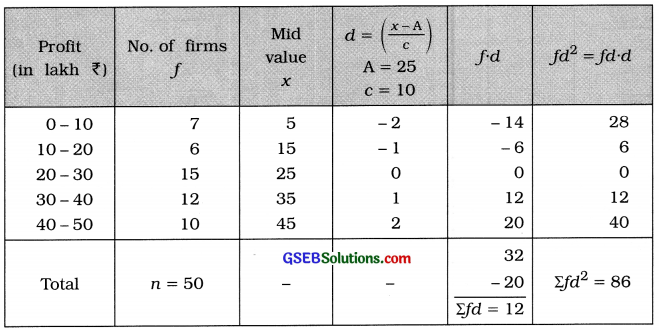
Mean:
x̄ = A + \(\frac{\Sigma f d}{n}\) × c
= 25 + \(\frac{12}{50}\) × 10
= 25 + \(\frac{12}{5}\)
= 25 + 2.4
= ₹ 27.4 lakh
Standard deviation of profit:

Question 5.
Find the standard deviation of age of the persons from the following distribution of 125 persons living in a society. Also find the coefficient of standard deviation.

Answer:
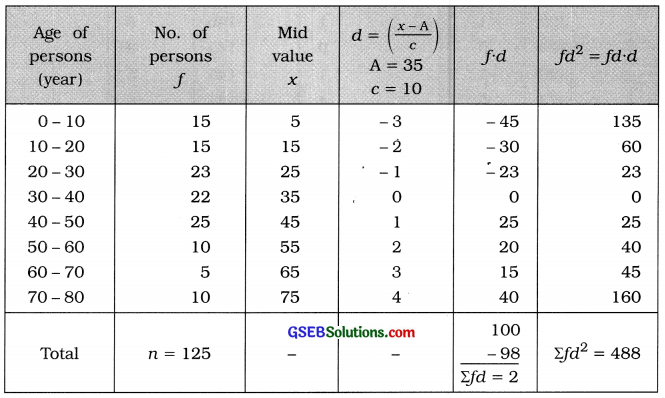
Mean:
x̄ = A + \(\frac{\Sigma f d}{n}\) × c
= 35 + \(\frac{2}{125}\) × 100
= 35 + \(\frac{20}{125}\)
= 35 + 0.16
= 35.16
Standard deviation of age:

Coefficient of standard deviation of age
= \(\frac{s}{\bar{x}}=\frac{19.76}{35.16}\) = 0.56