GSEB Solutions Class 11 Statistics Chapter 4 अपकिरण Ex 4

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 4 अपकिरण Ex 4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 4 अपकिरण Ex 4

विभाग – A

निम्न विकल्पों में से योग्य विकल्प का चयन कीजिए ।

प्रश्न 1.
निम्न में से कौन-सा सूत्र विस्तारगुणांक का है ?
(A) X_H – X_L
(B) \(\frac{x_H-x_L}{x_H+x_L}\)
(C) \(\frac{x_L-x_H}{x_L+x_H}\)
(D) X_L – X_H
उत्तर :
(B) \(\frac{x_H-x_L}{x_H+x_L}\)

प्रश्न 2.
अपकिरण के कौन से माप में अवलोकनों और उसका माध्य के अंतर का मानांक लिया जाता है ?
(A) औसत विचलन
(B) प्रमाप विचलन
(C) विस्तार
(D) चतुर्थक विचलन
उत्तर :
(A) औसत विचलन

प्रश्न 3.
निम्न में से कौन-सा माप इकाई से मुक्त है ?
(A) औसत विचलन
(B) चतुर्थक विचलन
(C) विस्तार
(D) विचरण गुणांक
उत्तर :
(D) विचरण गुणांक

प्रश्न 4.
अंतिम अवलोकनों का प्रभाव न्यूनतम होता हो ऐसा अपकिरण का माप कौन-सा है ?
(A) विस्तार
(B) प्रमाप विचलन
(C) चतुर्थक विचलन
(D) औसत विचलन
उत्तर :
(C) चतुर्थक विचलन

प्रश्न 5.
यदि समूह A का विचरण गुणांक समूह B के विचरण गुणांक से कम हो, तो कौन-सा समूह चलन की दृष्टि से अधिक स्थिर माना जाता है ?
(A) A
(B) B
(C) A और B दोनों
(D) कुछ नहि कह सकते
उत्तर :
(A) A

प्रश्न 6.
10 विद्यार्थियों के वजन (किग्रा में) निम्नानुसार है ।
53, 47, 60, 55, 71, 65, 61, 58, 63, 70 सूचना का विस्तार कितना ?
(A) 17
(B) 23
(C) 24
(D) 18
उत्तर :
(C) 24

प्रश्न 7.
एक सूचना का प्रथम और तृतीय चतुर्थक क्रमश: 30 और 50 हो, तो चतुर्थक विचलन गुणांक का मूल्य कितना होगा ?
(A) 0.25
(B) 50
(C) 4
(D) 25
उत्तर :
(A) 0.25

प्रश्न 8.
अवलोकन 5. 5, 5, 5. 5 के लिए अपकिरण का कोई भी माप क्या होगा ?
(A) 1
(B) 5
(C) 0
(D) 25
उत्तर :
(C) 0

प्रश्न 9.
एक चल के लिए माध्य 10 और विचरण गुणांक 60% हो, तो चल का विचरण कितना होगा ?
(A) 6
(B) 36
(C) 60
(D) 50
उत्तर :
(B) 36

प्रश्न 10.
एक शृंखला k₁, k₂, k₃, ……………… k_n का प्रमाप विचलन 5 है, तो
(i) k₁ + 2, k₂ + 2, k₃ + 2 ……………… k_n + 2
(ii) 3k₁, 3k₂, 3k₃, ………………… 3k_n शृंखला का प्रमाप विचलन क्या होगा ?
(A) (i) 7 (ii) 3
(B) (i) 5 (ii) 3
(C) (i) 5 (ii) 15
(D) (i) 7 (ii) 15
उत्तर :
(C) (i) 5 (ii) 15

प्रश्न 11.
एक चल x का माध्य 5 और प्रमाप विचलन 2 है, यदि y = 3x + 4 हो, तो चल y का माध्य और प्रमाप विचलन क्रमशः कितना होगा ?
(A) 19 और 6
(B) 15 और 49
(C) 19 और 10
(D) 15 और 10
उत्तर :
(A) 19 और 6

प्रश्न 12.
एक सूचना के अवलोकनों का माध्य और प्रमाप विचलन क्रमशः 45 और 5 है । यदि प्रत्येक अवलोकनों में अचल संख्या 5 जोड़ा जाय तो नई सूचना के अवलोकनों का विचरण गुणांक कितना होगा ?
(A) 10%
(B) 50%
(C) 11.11%
(D) 900%
उत्तर :
(A) 10%

विभाग – B

निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए ।

प्रश्न 1.
विस्तार की परिभाषा कीजिए ।
उत्तर :
सूचना के सबसे बड़े मूल्य का अवलोकन और सबसे छोटे मूल्य के अवलोकन के अन्तर को विस्तार (Range) कहते है, जिसे संकेत में R द्वारा प्रदर्शित किया जाता है ।

प्रश्न 2.
चतुर्थक विचलन की परिभाषा दीजिए ।
उत्तर :
सूचना के तृतीय चतुर्थक Q₃ और प्रथम चतुर्थक Q₁ के अन्तर को दो से भाग देने पर प्राप्त माप चतुर्थक विचलन कहलाता है, जिसे संकेत में Q_d द्वारा प्रदर्शित किया जाता है ।

प्रश्न 3.
दो या उससे अधिक समूहों की उसके चलन के संदर्भ में तुलना करने के लिए अपकिरण के कौन से प्रकार के मापों का उपयोग होता है ?
उत्तर :
दो या उससे अधिक समूहों की तुलना करने के लिए अपकिरण के सापेक्ष मापों जैसे प्रमाप विचलन गुणांक, विचरण गुणांक, विस्तार गुणांक, चतुर्थक विचलन गुणांक, औसत विचलन गुणांक का उपयोग होता है ।

प्रश्न 4.
अपकिरण के श्रेष्ठ माप कौन-सा है ?
उत्तर :
प्रमाप विचलन अपकिरण का श्रेष्ठ माप है ।

प्रश्न 5.
यदि दस विद्यार्थियों की ऊँचाई सेन्टिमीटर में दी गई हो तो उसके विचरण की इकाई क्या होगी ?
उत्तर :
विचरण की इकाई (सेन्टीमीटर)² में होगी ।

प्रश्न 6.
एक कंपनी पाईप लाईन का उत्पादन करती है । पाईप का व्यास की निम्नानुसार सूचना प्राप्त होती है, तो उस पर से पाईपलाईन के व्यास का विस्तार ज्ञात करो ।

उत्तर :
प्रथम वर्ग की अधःसीमा 20 है ∴ X_L = 20 और अंतिम वर्ग की उर्ध्वसीमा 120 है । ∴ X_H = 120
विस्तार R = X_H – X_L = 120 – 20
∴ विस्तार R = 100 से.मी.
पाईप लाईन के व्यास का विस्तार 100 सेमी. है ।

प्रश्न 7.
एक आवृत्ति वितरण का 25 वाँ तथा 75 वाँ शतांशक क्रमश: 72.18 तथा 103.99 है । इस सूचना का चतुर्थक विचलन ज्ञात कीजिए ।
उत्तर :
चतुर्थक विचलन Q_d = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{103.99-72.18}{2}\)
= \(\frac{31.81}{2}\) = = 15.905
P₂₅ = Q₁ = 72.18
P₇₅ = Q₃ = 103.99
चतुर्थक विचलन = 15.91

प्रश्न 8.
एक समूह के 7 विद्यार्थियों द्वारा 25 अंक की परीक्षा में प्राप्त अंक क्रमशः 20, 20, 20, 20, 20, 20, 20 है, तो उसके अंक का प्रमाप विचलन क्या होगा ?
उत्तर :
प्रमाप विचलन S = 0 होगा क्यों कि यदि चर के सभी अवलोकन समान हो तो अपकिरण का कोई भी माप 0 होता है ।

प्रश्न 9.
-1, 0, 4 अवलोकनों पर से औसत विचलन ज्ञात करो ।
उत्तर :

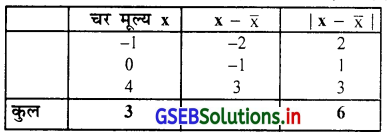
∴ \(\bar{x}=\frac{3}{3}\) औसत विचलन MD = \(\frac{\sum|x-\bar{x}|}{n}\)
\(\overline{\mathrm{X}}\) = 1 = \(\frac{6}{3}\) = 2
औसत विचलन 2 होगा ।

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
निम्न की परिभाषा दीजिए ।
(i) औसत विचलन
(ii) प्रमाप विचलन
(iii) विचरण गुणांक
उत्तर :
(i) औसत विचलन : सूचना के अवलोकन मूल्यों का उसके माध्य से लिए गये मानांक विचलनों का औसत मूल्य । उसे संकेत में MD से दर्शाया जाता है ।

(ii) प्रमाप विचलन : दी गई सूचना के अवलोकनों के माध्य से लिये गये विचलन के वर्गों के कुल योग को अवलोकनों की कुल संख्या से भाग देने पर प्राप्त मूल्य के धन वर्ग मूल को प्रमाप विचलन कहते है । जिसे संकेत में ‘S’ से दर्शाया जाता है ।

(iii) विचरण गुणांक : प्रमाप विचलन पर आधारित अपकिरण का प्रतिशत सापेक्ष माप को विचरण गुणांक कहा जाता है ।

प्रश्न 2.
अपकिरण का निरपेक्ष और सापेक्ष माप का अर्थ लिखिए ।
उत्तर :
निरपेक्ष माप : यदि अपकिरण के मापों को अवलोकन मूल्य की इकाई द्वारा प्रदर्शित किया जाय तो उस माप को निरपेक्ष अपकिरण कहते है ।

सापेक्ष माप : सूचना के समूहों के माप की तुलना करनी हो तब सूचना के अवलोकन मूल्यों की इकाईयाँ भिन्न-भिन्न होने से अपकिरण का निरपेक्ष माप उपयोगी नहीं हो सकता । इस परिस्थिति में अपकिरण के सापेक्ष माप ज्ञात किये जाते है, जो इकाई से मुक्त है । जिससे दो या दो से अधिक सूचना समूहों की तुलना संभव हो पाती है ।

अपकिरण का सापेक्ष माप =

प्रश्न 3.
अपकिरण के निरपेक्ष मापों के नाम दीजिए ।
उत्तर :
अपकिरण के निरपेक्ष माप निम्नलिखित है :

1. विस्तार
2. चतुर्थक विचलन
3. औसत विचलन
4. प्रमाप विचलन

प्रश्न 4.
अवलोकनों और उसके माध्य में से लिये गये विचलनों पर आधारित अपकिरण के कौन से माप है ?
उत्तर :
अवलोकनों और उसके माध्य में से लिये गये विचलनों पर आधारित अपकिरण के माप औसत विचलन और प्रमाप विचलन है।

प्रश्न 5.
6, 11, -3, 0, 8 अवलोकनों का विस्तार और विस्तार गुणांक ज्ञात करो ।
उत्तर :
यहाँ X_H = 11 और X_L = -3 है ।
∴ विस्तार R = X_H – X_L
= 11 – (-3) = 14
∴ विस्तार गुणांक CR = \(\frac{x_{\mathrm{H}}-\mathrm{x}_{\mathrm{L}}}{\mathrm{x}_{\mathrm{H}}+\mathrm{x}_{\mathrm{L}}}\)
= \(\frac{14}{11+(-3)}=\frac{14}{8}\)
विस्तार गुणांक = 1.75

प्रश्न 6.
निम्न अवलोकनों पर से चतुर्थक विचलन गुणांक ज्ञात कीजिए ।
8, 15, 2, 11, 20, 3, 5
उत्तर :
चढ़ते क्रम में गठित करने पर 2, 3, 5, 8, 11, 15, 20
प्रथम चतुर्थक Q₁ = \(\frac{\mathrm{n}+1}{4}\) वाँ अवलोकन मूल्य
= \(\frac{7+1}{4}=\frac{8}{4}\) = 2 वाँ अवलोकन मूल्य
∴ Q₁ = 3
Q₃ = 3(\(\frac{n+1}{4}\)) वाँ अवलोकन मूल्य
= 3(\(\frac{7+1}{4}\))
= \(\frac{3 \times 8}{4}\) = 6 वाँ अवलोकन मूल्य
∴ Q₃ = 15
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{\mathrm{Q}_3+\mathrm{Q}_1}=\frac{15-3}{15+3}=\frac{12}{18}\)
∴ चतुर्थक विचलन गुणांक = 0.67

प्रश्न 7.
निम्न दिये गये अवलोकनों पर से औसत विचलन ज्ञात कीजिए ।
3, 8, 1, 7, 6
उत्तर :

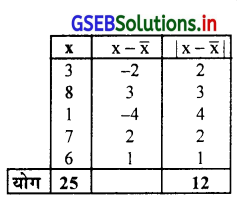
माध्य \(\overline{\mathrm{x}}=\frac{25}{5}\) औसत विचलन MD =
\(\frac{\Sigma|x-\vec{x}|}{n}=\frac{12}{5}\) ∴ \(\overline{\mathrm{x}}\) = 5 ∴ MD = 2.4

प्रश्न 8.
यदि \(\overline{\mathrm{x}}\) = 25 और विचरण गुणांक 20% हो तो विचरण ज्ञात कीजिए ।
उत्तर :
यहाँ \(\overline{\mathrm{x}}\) = 25 विचरण गुणांक C-V = 20
∴ विचरण गुणांक = \(\frac{\mathrm{s}}{\overline{\mathrm{X}}}\) × 100
20 = \(\frac{s}{25}\) × 100
\(\frac{20 \times 25}{100}\) = S
∴ S = 5
∴ विचरण S² = (5)
∴ विचरण (S²) = 25

प्रश्न 9.
1, 2, 3, 4, 5 अवलोकनों के लिए प्रमाप विचलन ज्ञात करो ।
उत्तर :

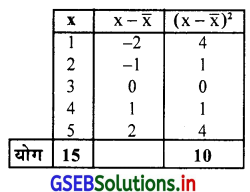
माध्य \(\bar{x}=\frac{\Sigma x}{n}=\frac{15}{5}\)
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma(\mathrm{x}-\overline{\mathrm{x}})^2}{\mathrm{n}}}=\sqrt{\frac{10}{5}}=\sqrt{2}\)
∴ \(\overline{\mathbf{X}}\) = 3
∴ प्रमाप विचलन = 1.41
∴ S = 1.41

प्रश्न 10.
निम्न में से कौन-सा कारखाना प्रतिदिन उत्पादन के संदर्भ में अधिक स्थिर है ?

	कारखाना A	कारखाना B
औसत प्रतिदिन उत्पादन (इकाई)
प्रमाप विचलन (इकाई)

उत्तर :
कारखाना A और B की तुलना करने के लिए दोनों का विचरण गुणांक ज्ञात करेंगे ।
कारखाना A का विचरण गुणांक = \(\frac{\mathrm{S}}{\overline{\mathrm{x}}}\) × 100
= \(\frac{10}{50}\) × 100
∴ विचरण गुणांक = 20%
कारखाना B का विचरण गुणांक = \(\frac{\mathrm{S}}{\overline{\mathrm{x}}}\) × 100 = \(\frac{12}{48}\) × 100
∴ विचरण गुणांक = 25%
कारखाना A के उत्पादन का विचरण गुणांक कम है इसलिए A उत्पादन के संदर्भ में अधिक स्थिर है ।

प्रश्न 11.
एक सूचना के समूह का 25 वाँ और 75 वाँ शतमक क्रमशः 20 और 36 है, तो चतुर्थक विचलन गुणांक ज्ञात कीजिए ।
उत्तर :
P₂₅ = Q₁ ∴ Q₁ = 20
P₂₅ = Q₃ ∴ Q₃ = 36
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{\mathrm{Q}_3+\mathrm{Q}_1}=\frac{36-20}{36+20}=\frac{16}{56}\)
∴ चतुर्थक विचलन गुणांक = 0.29

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
अपकिरण का अर्थ समझाइये और उसके भिन्न भिन्न माप बताइये ।
उत्तर :
औसत का माप दी गई सूचना का प्रतिनिधि के रूप में माप है, और उसके द्वारा केवल एक ही संख्या से दी गई सूचना की केन्द्रीय स्थिति प्रस्तुत करता है। परंतु दी गई सूचना के सभी अवलोकन सूचना के औसत के समान नहीं होते है। इससे सूचना के अध्ययन में औसत का माप पूर्ण नहीं मान सकते है । इसके अतिरिक्त कितनी ही बार दो सूचनाओं का औसत का मूल्य समान होते हुए उसके मूल्यों में फैलाव अलग-अलग होता है । ऐसी परिस्थिति में मात्र औसत मूल्यों की सहायता से सूचना की तुलना गलत दिशा देती है । इससे सूचना की रचना और उसके मूल्यों के बीच रहे अंतर के विषय में अध्ययन करने के उद्देश्य से तथा दो या उससे अधिक सूचनाओं की तुलना करने के लिए औसत माप के अलावा दूसरे माप की आवश्यकता होती है । यह माप उस अपकिरण का माप है, जो दी गई सूचना की रचना के स्वरूप का अंदाज देता है ।

“अपकिरण अर्थात् सूचना के अवलोकन मूल्य को औसत के माप मूल्य से कितने अंतर पर स्थित हुए है उसके अध्ययन को ।’ अन्य शब्दों में कहे तो अपकिरण द्वारा सारगर्भित शृंखला की रचना के विषय में जानकारी प्राप्त करना है। संक्षेप में सूचना के अवलोकनों में रही सममितीयता की त्रुटी अर्थात् अपकिरण ।

अपकिरण के भिन्न भिन्न माप :

1. विस्तार : सबसे बड़ा और छोटा अवलोकन के अंतर से प्राप्त किया जाता है । संकेत में R से दर्शाया जाता है ।
2. चतुर्थक विचलन : तृतीय चतुर्थक Q₃ और प्रथम चतुर्थक Q₁ के अंतर को 2 से भाग देकर प्राप्त होता है। उसे संकेत में Q_d से दर्शाया जाता है ।
3. औसत विचलन : सूचना के अवलोकनों के उसके माध्य से लिए गए विचलनों के मानांक की औसत किंमत को औसत विचलन कहते है । उसे संकेत में MD से दर्शाया जाता है ।
4. प्रमाप विचलन : सूचना के अवलोकन उसके माध्य से लिए गए विचलनों के वर्गों के योग को अवलोकन की संख्या से भाग देने पर प्राप्त मूल्य के धन वर्गमूल को सूचना का प्रमाप विचलन कहते है । उसे संकेत में S से दर्शाया जाता है ।

प्रश्न 2.
अपकिरण के इच्छनीय लक्षण बताइये ।
उत्तर :
अपकिरण के इच्छनीय लक्षण निम्नलिखित है :

1. अपकिरण के माप की परिभाषा स्पष्ट और स्थिर होनी चाहिए ।
2. अपकिरण समझने में सरल और गणना में भी सरल होनी चाहिए ।
3. उसकी गणना में समग्र अवलोकनों का उपयोग होना चाहिए ।
4. उसके मूल्य पर सूचना के सीमान्त अवलोकन मूल्यों का प्रभाव कम होना चाहिए ।
5. उस पर न्यादर्श का प्रभाव कम होना चाहिए ।
6. बीजगणितीय विवेचन के लिए माप अनुकूल होना चाहिए ।
7. आंकडाशास्त्र की प्रचलित पद्धतियों में उस माप का उपयोग होना चाहिए ।

प्रश्न 3.
विस्तार के लाभ (गुण) तथा अवगुण लिखिए ।
उत्तर :
विस्तार के गुण-अवगुण निम्नलिखित है :
गुण :

1. विस्तार की परिभाषा स्पष्ट तथा समझने में सरल है ।
2. उसकी गणना सरल है ।
3. उनके अवलोकनों पर एक दृष्टि डालने से ही विस्तार ज्ञात कर सकते है ।
4. सूचना में चलन कम हो तो विस्तार उपयोगी माप है ।
5. गुणवत्ता नियंत्रण के कार्य में अपकिरण के माप के रूप में वह अधिक उपयोगी माप है ।

अवगुण :

1. उसकी गणना में सभी अवलोकनों का उपयोग नहीं होता है ।
2. विस्तार पर न्यादर्श का प्रभाव अधिक होता है ।
3. वह बैजिक क्रिया के लिए अनुकूल माप नहीं है ।
4. खुले सिरे की आवृत्ति-वितरण में यह माप ज्ञात नहीं कर सकते है ।
5. आंकडाशास्त्र के उच्च अभ्यास में इसका उपयोग कम होता है ।

प्रश्न 4.
चतुर्थक विचलन के गुण-अवगुण लिखिए ।
उत्तर :
चतुर्थक विचलन के गुण-अवगुण निम्नलिखित है :
गुण :

1. उसकी परिभाषा स्पष्ट और स्थिर है ।
2. उसकी गणना सरल है ।
3. इस पर अवलोकन के सीमान्त मूल्यों का प्रभाव नहीं पड़ता है ।
4. निर्वतमुखी (खुलाशिरा) वाला आवृत्ति वितरण के लिए अपकिरण का यह एक मात्र माप की गणना हो सकती है ।
5. जब सूचना के मध्य के 50% अवलोकनों का अपकिरण का अध्ययन करना हो तब यह माप अधिक अनुकूल है ।

अवगुण :

1. उसकी गणना सभी मूल्यों पर आधारित नहीं है । सूचना के प्रथम 25% और अंतिम 25% अवलोकनों की अवगणना की जाती है ।
2. यह अन्य बीजगणितीय विवेचन के लिए अनुकूल माप नहीं है ।
3. आंकडाशास्त्र के उच्च अभ्यास में इस माप का उपयोग नहीवत् है ।
4. इस पर न्यादर्श का प्रभाव अधिक मात्रा में होता है ।
5. यह माप स्थिर नहीं होने से सूचनाओं की तुलना हमेशा सही नहीं होती है ।

प्रश्न 5.
औसत विचलन के गुण-अवगुण लिखिए ।
उत्तर :
औसत विचलन के गुण-अवगुण निम्नलिखित है :
गुण :

1. माध्य विचलन की परिभाषा स्पष्ट है ।
2. इसकी गणना में समग्र अवलोकनों का उपयोग होता है ।
3. प्रमाप विचलन की अपेक्षा गणना सरल है ।
4. उस पर अंतिम अवलोकनों का कम प्रभाव पड़ता है ।
5. विस्तार और चतुर्थक विचलन की अपेक्षा विश्वसनीय है ।
6. सामाजिक शास्त्रों के अध्ययन में यह उपयोगी माप है ।
7. अवलोकन का माध्य से अन्तर का मानांक लेते है । अन्तर के मानांक में अन्तर योग्य माप है ।

अवगुण :

1. विस्तार व चतुर्थक विचलन की अपेक्षा इसकी गणना कठिन है ।
2. यह माप अन्य बीजगणितीय विवेचन के लिए अनुकूल नहीं है ।
3. यह माप मानांक पर आधारित होने से आंकड़ाशास्त्र के उच्च अध्ययन में इसका उपयोग कम होता है ।
4. उसकी गणना में विचलन के चिन्हों की उपेक्षा की जाती है जो गाणितिक रूप से तार्किक नहीं है ।

प्रश्न 6.
प्रमाप विचलन के गुण-अवगुण लिखिए ।।
उत्तर :
प्रमाप विचलन के गुण-अवगुण निम्नलिखित है :
गुण :

1. इसकी परिभाषा स्पष्ट और स्थिर है ।
2. इसकी गणना में समग्र अवलोकनों का उपयोग होता है ।
3. अन्य अपकिरण के मापों की अपेक्षा अधिक विश्वसनीय एवं श्रेष्ठ माप है ।
4. यह बीजगणितीय विवेचन के लिए अनुकूल माप है ।
5. प्रमाप विचलन माध्य के आधार पर ज्ञात किया जाता है, जिससे माध्य विचलन की अपेक्षा इन माप की गणना में अधिक एकरूपता है।
6. अपकिरण के अन्य मापों की अपेक्षा प्रमाप विचलन पर न्यादर्शों का प्रभाव कम पड़ता है ।
7. अपकिरण के अन्य मापों की अपेक्षा प्रमाप विचलन का उपयोग अधिक होता है ।

अवगुण :

1. प्रमाप विचलन ज्ञात करने में व समझने में अन्य मापों की तुलना में कठिन है ।
2. इस माप पर अंतिम अवलोकनों का प्रभाव अधिक होता है ।
3. यदि खुल्ले शिरावाला आवृत्ति वितरण हो तो प्रमाप विचलन ज्ञात नहि हो सकता ।

प्रश्न 7.
प्रमाप विचलन अर्थात् क्या ? उसे अपकिरण का श्रेष्ठ माप क्यों कहते है ?
उत्तर :
सूचना के अवलोकन के माध्य से लिये गये विचलन के वर्गों के कुल योग को अवलोकनों की कुल संख्या से भाग देने पर प्राप्त मूल्य के धन वर्ग मूल को प्रमाप विचलन कहते है । जिसे संकेत में ‘S’ से दर्शाया जाता है ।

प्रमाप विचलन के मूल्य पर सूचना के छोटे और बड़े अवलोकन का प्रभाव अधिक होता है। उसकी गणना अपकिरण के अन्य मापों की अपेक्षा कठिन है। फिर भी उसकी परिभाषा स्पष्ट है । सूचना के सभी अवलोकनों का उपयोग होता है। बीजगणितीय क्रियाओं के लिए उपयोगी माप है अर्थात् अपकिरण के इच्छनीय लक्षणों का समावेश प्रमाप विचलन में होता है और व्यवहार में अपकिरण के माप के रूप में अत्यंत उपयोगी और विश्वसनीय है । इसलिए उसे अपकिरण का श्रेष्ठ माप
के रूप में उपयोग में लिया जाता है।

प्रश्न 8.
विचरण गुणांक पर टिप्पणी लिखिए ।
उत्तर :
जब दो या दो से अधिक सूचना के समूहों की तुलना करनी हो तब सामान्य रूप से प्रमाप विचलन गुणांक का उपयोग किया जाता है, परंतु दो या दो से अधिक सूचना समूहों के अपकिरण का योग्य व सटीक तुलना करने के लिए कार्लपियर्सन द्वारा सूचित विचरण गुणांक (Coefficient of Variation) माप का उपयोग किया जाता है । प्रमाप विचलन गुणांक को 100 से गुणाकार करने से विचरण गुणांक प्राप्त होता है । विचरण गुणांक = प्रमाप विचलन गुणांक × 100
= × 100
= \(\frac{\mathbf{S}}{\overline{\mathbf{X}}}\) × 100
यह सापेक्ष माप है । प्रतिशत दर्शक होने से अपकिरण की तुलना में इस माप का सब से अधिक उपयोग होता है । जिस श्रृंखला का विचरण गुणांक कम हो उसे अधिक स्थिर और जिस शृंखला का विचरण गुणांक अधिक हो उस श्रृंखला के मूल्य अस्थायी या असंगत है ऐसा कहा जायेगा।

प्रश्न 9.
एक नर्सरी में 100 पौधों पर फूल की संख्या की निम्न सूचना पर से प्रति पौधों पर फूल की संख्या का चतुर्थक विचलन ज्ञात करो ।

उत्तर :

फूल की संख्या xi	पौधों की संख्या f	संचयी आवृत्ति cf
11	5	5
13	8	13
15	13	26
17	20	46
19	22	68
21	18	86
23	10	96
25	4	100

Q₁ = \(\frac{n+1}{4}\) वाँ अवलोकन मूल्य
= \(\frac{100+1}{4}=\frac{101}{4}\)
= 25.25 वाँ अवलोकन मूल्य cf के अनुसार 15 है ।
∴ Q₁ = 15 फूल
Q₃ = \(\frac{3(n+1)}{4}\)वाँ अवलोकन मूल्य
= 3 (\(\frac{100+1}{4}\)) = 3 × 25.25
= 75.75 वाँ अवलोकन मूल्य cf के अनुसार 21 है ।
∴ Q₃ = 21
चतुर्थक विचलन Q_d = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{21-15}{2}=\frac{6}{2}\)
∴ चतुर्थक विचलन Q_d = 3

प्रश्न 10.
होकी की एक स्पर्धा में 16 मेच में हुए गोल की संख्या का आवृत्ति वितरण निम्नानुसार है । उस पर से प्रतिमेच हुए गोल की संख्या का औसत विचलन ज्ञात करो ।

उत्तर :
आवृत्ति वितरण असतत प्रकार का है इस लिए निम्नानुसार सारणी बनायेंगे ।

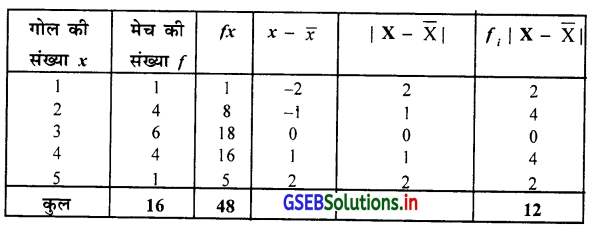
माध्य \(\bar{X}=\frac{\sum f x}{n}=\frac{48}{16}\)
∴ \(\overline{\mathrm{x}}\) = 3 गोल
औसत विचलन MD = \(\frac{\Sigma \mathrm{fi}|\mathrm{x}-\overline{\mathrm{x}}|}{\mathrm{n}}=\frac{12}{16}\)
∴ MD = 0.75 गोल
गोल की संख्या का औसत विचलन MD = 0.75 गोल

प्रश्न 11.
प्रचलित संकेतों में Σd = 25, Σd² = 272, n = 100 और काल्पित माध्य 4 है । और सूचना पर से विचरण गुणांक
ज्ञात कीजिए ।
उत्तर :
विचरण गुणांक ज्ञात करने के लिए माध्य और प्रमाप विचलन ज्ञात करेंगे ।
माध्य \(\overline{\mathrm{x}}\) = A + \(\frac{\Sigma \mathrm{d}}{\mathrm{n}}\) = 4 + \(\frac{25}{100}\) = 4 + 0.25
∴ \(\overline{\mathrm{x}}\) = 4.25

= \(\sqrt{2.72-0.0625}=\sqrt{2.6575}\)
∴ S = 1.63
विचरण गुणांक C.V = \(\frac{\mathrm{S}}{\overline{\mathrm{X}}}\) × 100 = \(\frac{1.63}{4.25}\) × 100
विचरण गुणांक = 38.35%

प्रश्न 12.
निम्न सूचना पर से मिश्र प्रमाप विचलन ज्ञात करो ।

विवरण	समूह A	समूह B
अवलोकनों की संख्या	50	60
माध्य	113	120
प्रमाप विचलन	6	7

उत्तर :
यहाँ n₁ = 50 \(\bar{x}_1\) = 113 S₁ = 6 n₂ = 60 \(\bar{x}_2\) = 120 S₂ = 7
मिश्र माध्य

∴ Sc = 7.43
मिश्र प्रमाप विचलन Sc = 7.43

प्रश्न 13.
10 अवलोकनों का योग 80 और अवलोकनों के वर्गों का योग 800 है । इस सूचना का विचरण गुणांक ज्ञात करो ।
उत्तर :
विचरण गुणांक ज्ञात करने के लिए माध्य और प्रमाप विचलन ज्ञात करेंगे ।
माध्य \(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{x}}{\mathrm{n}}=\frac{80}{10}\)
∴ \(\overline{\mathrm{X}}\) = 8
विचरण गुणांक = \(\frac{\mathrm{s}}{\overline{\mathrm{x}}}\) × 100
= \(\frac{4}{8}\) × 100
∴ विचरण गुणांक = 50%
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma x^2}{n}-(\bar{x})^2}=\sqrt{\frac{800}{10}-(8)^2}\)
= \(\sqrt{80-64}=\sqrt{16}\)
∴ S = 4

विभाग – E

निम्न के हल प्राप्त कीजिए ।

प्रश्न 1.
भाषा की 50 अंक की परीक्षा में 30 विद्यार्थियों द्वारा प्राप्त अंक का आवृत्ति वितरण निम्नानुसार है, तो आवृत्ति वितरण का औसत विचलन ज्ञात करो ।

उत्तर :

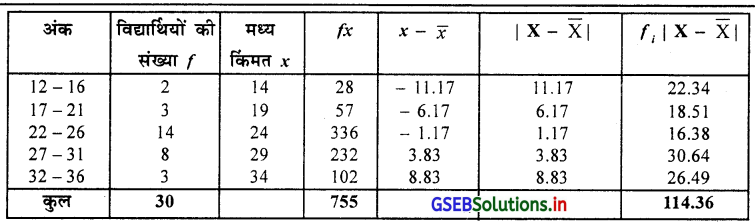
माध्य \(\overline{\mathrm{X}}=\frac{\sum f x}{n}=\frac{755}{30}\)
∴ \(\overline{\mathrm{x}}\) = 25.17 अंक
औसत विचलन MD = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}|\mathrm{x}-\overline{\mathrm{x}}|}{\mathrm{n}}=\frac{114.36}{30}\)
∴ MD = 3.81 अंक
30 विद्यार्थियों द्वारा प्राप्त किये अंक का औसत विचलन 3.81 अंक है ।

प्रश्न 2.
निम्न 50 कंपनीओं के विज्ञापन-खर्च का आवृत्ति वितरण पर से कंपनी के विज्ञापन खर्च का चतुर्थक विचलन ज्ञात कीजिए ।

उत्तर :
संचयी आवृत्ति वितरण ज्ञात करेंगे ।

विज्ञापन खर्च (हजार रु.)	कंपनी की संख्या f	संचयी आवृत्ति cf
0 – 5	3	3
5 – 15	8	11
15 – 30	15	26
30 – 40	10	36
40 – 60	8	44
60 – 100	6	50
कुल	50

Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{50}{4}\) = 12.5 वाँ अवलोकन मूल्य of की सारणी के अनुरूप Q वर्ग = 15 – 30
Q₁ = L + \(\frac{\frac{n}{4}-c f}{f}\) × c
जहाँ L = 15, \(\frac{n}{4}\) = 11, f = 15, c = 15
= 15 + \(\frac{12.5-11}{15}\) × 15 = 15 + 1.5
∴ Q₃ = 3 (\(\frac{n}{4}\)) वाँ अवलोकन मूल्य
= 3 (\(\frac{50}{4}\)) = 3 × 12.5
= 37.5 वाँ अवलोकन मूल्य of की सारणी के अनुरूप Q₃ वर्ग = 40 – 60
Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
जहाँ L = 40, 3(\(\frac{n}{4}\)) = 37.5, cf = 36, f = 8, c = 20
= 40 + \(\frac{37.5-36}{8}\) × 20 = 40 + \(\frac{1.5 \times 20}{8}\) = 40 + \(\frac{30}{8}\) = 40 + 3.75
∴ Q₃ = 43.75
चतर्थक विचलन = Q_d = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{43.75-16.5}{2}=\frac{27.25}{2}\)
∴ Q_d = 13.63

प्रश्न 3.
एक बेट्समेन द्वारा खेली गई 100 किक्रेट की वन-डे मेच में किये गये रन का विवरण निम्नानुसार है । यह सूचना पर से बेट्समेन द्वारा किये गये रन का प्रमाप विचलन ज्ञात कीजिए ।

उत्तर :
सिर्फ प्रमाप विचलन ज्ञात करना है इसलिए माध्य के मूल्य की आवश्यकता नहि है । संक्षिप्त विधि का उपयोग करेंगे । यहाँ काल्पित माध्य A = 35 और वर्गलम्बाई C = 10

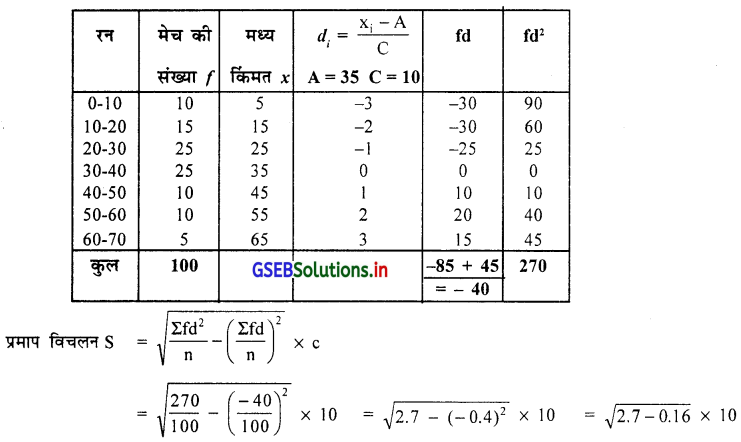
= \(\sqrt{2.54} \times 10\) × 10 = 1.594 × 10
∴ प्रमाप विचलन S = 15.94 रन
बेट्समेन द्वारा किये गये रन का प्रमाप विचलन 15.94 रन है ।

प्रश्न 4.
कोलेज के 220 विद्यार्थियों द्वारा किसी एक परीक्षा में प्राप्त अंक का विवरण निम्नानुसार है । उस पर से विद्यार्थियों के अंक का चतुर्थक विचलन ज्ञात करो ।

उत्तर :
आवृत्ति वितरण अनिवारक सतत (अखंडित) प्रकार का दिया है । चतुर्थक विचलन की गणना में प्रथम चतुर्थक और तृतीय चतर्थक का उपयोग करेंगे । इसके लिए अनिवारक को निवारक सतत आवृत्ति तैयार करेंगे ।

अंक	विद्यार्थियों की संख्या f	संचयी आवृत्ति cf
– 0.5 – 9.5	30	30
9.5 – 19.5	50	80
19.5 – 29.5	64	144
29.5 – 39.5	42	186
39.5 – 49.5	29	215
49.5 या उससे अधिक	5	220
कुल	220

प्रथम चतुर्थक Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{220}{4}\) = 55 वाँ अवलोकन मूल्य of की सारणी के अनुरूप Q वर्ग = 10 – 19 है । ∴ 9.5 – 19.5
∴ Q₁ = L + \(\frac{\frac{n}{4}-c f}{f}\) × c
जहाँ L = 9.5, \(\frac{n}{4}\) = 55, cf = 30, f = 50, c = 10
= 9.5 + \(\frac{55-30}{50}\) × 10 = 9.5 + \(\frac{25 \times 10}{50}\) = 9.5 + 5
∴ Q₁ = 14.5 अंक
तृतीय चतुर्थक Q₃ = 3 (\(\frac{\mathrm{n}}{4}\)) वाँ अवलोकन मूल्य
∴ = 3 (\(\frac{220}{4}\)) = 3 × 55
= 165 वाँ अवलोकन मूल्य cf के अनुरूप Q₃ वर्ग 29.5 – 39.5
Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
जहाँ L = 29.5, 3 (\(\frac{\mathrm{n}}{4}\)) = 165 cf = 144, f = 42, c = 10
= 29.5 + \(\frac{165-144}{42}\) × 10 = 29.5 + \(\frac{210}{42}\) = 29.5 + 5
∴ Q₃ = 34.5 अंक
चतुर्थक विचलन Q_d = \(=\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{34.5-14.5}{2}=\frac{20}{2}\)
∴ चतुर्थक विचलन Q_d = 10 अंक
विद्यार्थियों द्वारा प्राप्त अंक का चतुर्थक विचलन 10 अंक है ।

प्रश्न 5.
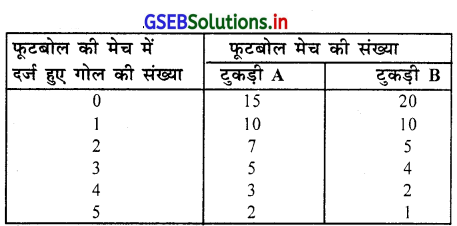
फूटबोल के खेल में दो टुकड़ी द्वारा निम्नानुसार गोल किये गए । कौन-सी टुकड़ी का खेल सुसंगत है ?

उत्तर :
दो टुकड़ी की तुलना करने के लिए दोनों टुकड़ी का विचरण-गुणांक ज्ञात करेंगे । उसके लिए निम्नानुसार सारणी बनायेंगे ।
टुकड़ी A:


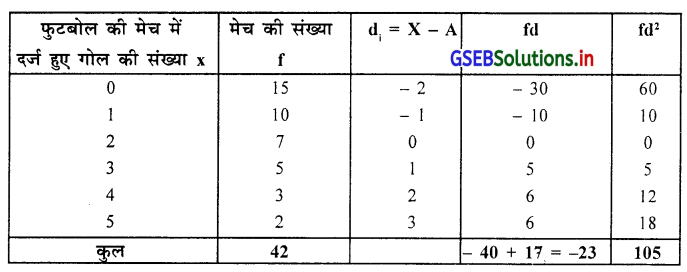
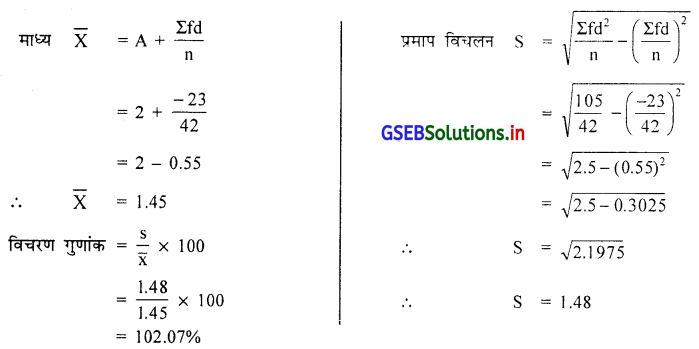
टुकड़ी A का विचरण गुणांक 102.07% है ।

टुकड़ी B :


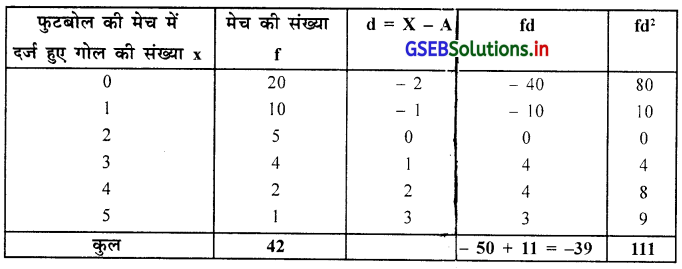
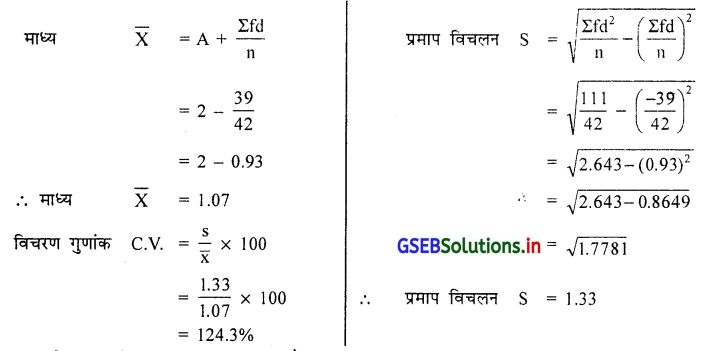
टुकड़ी B का विचरण गुणांक 124.3% है ।
टुकड़ी A का विचरण गुणांक टुकड़ी B की अपेक्षा कम है । इसलिए टुकड़ी A का खेल अधिक सुसंगत है ।

प्रश्न 6.
100 अवलोकनोंवाली एक श्रृंखला का माध्य व प्रमाप विचलन क्रमशः 40 और 10 है । गणना करते समय दो अवलोकनों का मूल्य भूल से 3 और 27 के बदले में 30 और 70 ले लिया गया हो तो सुधारा हुआ माध्य व प्रमाप विचलन ज्ञात कीजिए ।
उत्तर :
यहां n = 100, \(\) = 40, s = 10
गलत अवलोकन = 30, 70
सहि अवलोकन = 3, 27
माध्य \(\bar{X}=\frac{\Sigma x}{n}\)
∴ 40 = \(\frac{\Sigma x}{100}\)
∴ ΣX = 4000

सहि
Σx = 4000 – (30 + 70) + (3 + 27)
= 4000 – 100 + 30
= 3930
∴ सहि माध्य = \(\frac{3930}{100}\)
∴ सहि माध्य \(\bar{X}\) = 39.3

प्रमाप विचलन :
S = \(\sqrt{\frac{\Sigma \mathrm{x}^2}{\mathrm{n}}-(\overline{\mathrm{x}})^2}\)
10 = \(\sqrt{\frac{\Sigma \mathrm{x}^2}{100}-(40)^2}\)
∴ 100 = \(\frac{\Sigma \mathrm{x}^2}{100}\) – 1600 (वर्ग करने पर)
100 + 1600 = \(\frac{\Sigma \mathrm{x}^2}{100}\)
170000 = Σx²
∴ Σx² = 170000
सहि Σx² = 170000 – (30² + (70)²) + ((3)² + (27)²)
= 170000 – (900 + 4900) + (9 + 729)
= 170000 – 5800 + 738
= 164938
सहि Σx = 3930 है अथवा सुधार हुआ माध्य रखो ।
सहि प्रमाप विचलन = \(\sqrt{\frac{164938}{100}-\left(\frac{3930}{100}\right)^2}\)
= \(\sqrt{1649.38-(39.3)^2}=\sqrt{104.89}\) = 10.24
सहि माध्य सुधारा हुआ 39.3 और सहि प्रमाप विचलन सुधारा हुआ = 10.24 है ।

प्रश्न 7.
एक कारखाना में उत्पादित होती वस्तुओं का कुल खर्च का विधेय y = 10 + 3x है, जहाँ, x यह उत्पादित इकाईयों की संख्या और y यह x इकाईयों का कुल उत्पादन-खर्च दर्शाता है । कारखाना में प्रतिदिन उत्पादन होती वस्तुओं की इकाईयों की संख्या का विस्तार 50, चतुर्थक विचलन 5, औसत विचलन 8 और प्रमाप विचलन 10 है, तो यह सूचना पर से कुल । खर्च y का विस्तार, चतुर्थक विचलन और प्रमाप विचलन प्राप्त करो ।
उत्तर :
x उत्पादित इकाईयों की संख्या दर्शाता है ओर y कुल खर्च प्रदर्शित करता है ।
⇒ कुल खर्च y के लिए :
विस्तार = y = 3 × Rx में x = 50 रखने पर
∴ y = 3 × 50
∴ Ry = 150
चतुर्थक विचलन Q_dy = 3 × Q_dx = 3 × 5
∴ Q_dy = 15
औसत विचलन M_DY = 3 × M_DX = 3 × 8
∴ M_DY = 24
प्रमाप विचलन S_Y = 3 × S_X = 3 × 10
∴ S_Y = 30
कुल खर्च y का विस्तार R_y = 150
कुल खर्च y का चतुर्थक विचलन Q_dy = 15
कुल खर्च y का औसत विचलन M_DY = 24
कुल खर्च y का प्रमाप विचलन S_Y = 30 है ।

विभाग – F

निम्न के हल प्राप्त कीजिए ।

प्रश्न 1.
एक शहर में आकस्मिक बीमारी में मरीज अपने फेमिली डोक्टर को अपने घर पर बीमारी की जाँच के लिए बुलाते है। उस शहर के 80 डोक्टर की उनके मरीजों की जाँच की निम्न सूचना पर से विस्तार, विस्तार गुणांक, चतुर्थक विचलन, चतुर्थक विचलन गुणांक, औसत विचलन और औसत विचलन गणांक ज्ञात कीजिए ।

उत्तर :
चतुर्थक विचलन और औसत विचलन की गणना के लिए निम्नानुसार सारणी बनायेंगे ।

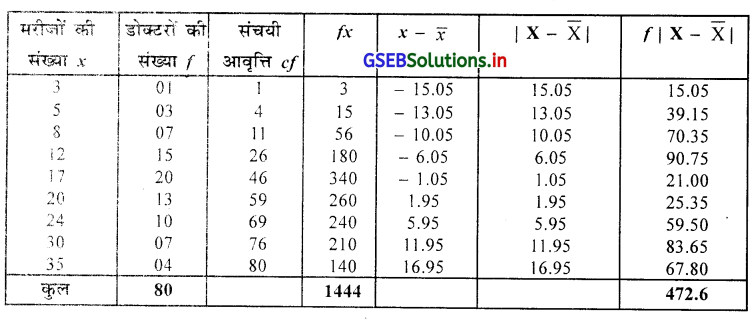
माध्य \(\bar{X}=\frac{\Sigma x}{n}=\frac{1444}{80}\) = 18.05
विस्तार X_H = 35 X_L = 3
R = X_H – X_L = 35 – 3
R = 32
विस्तार गुणांक = \(\frac{\mathrm{R}}{\mathrm{x}_{\mathrm{H}}-\mathrm{x}_{\mathrm{L}}}=\frac{32}{35+3}=\frac{32}{38}\)
∴ विस्तार गुणांक = 0.84

⇒ चतुर्थक विचलन :
प्रथम चतुर्थक Q₁ = \(\frac{n+1}{4}\) वाँ अवलोकन मूल्य
= \(\frac{80+1}{4}=\frac{81}{4}\) = 20.25 वाँ अवलोकन संचयी आवृत्ति के अनुरूप 12 है ।
∴ Q₁ = 12
तृतीय चतुर्थक Q₃ = 3(\(\frac{n+1}{4}\)) वाँ अवलोकन मूल्य = 3 (\(\frac{80+1}{4}\)) 3 (20.25)
= 60.75 वाँ अवलोकन के अनुरूप अवलोकन cf की सारणी पर से 24 है ।
∴ Q₃ = 24
अब चतुर्थक विचलन Q_d = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{24-12}{2}=\frac{12}{2}\) = 6
चतुर्थक विचलन गुणांक \(\frac{Q_3-Q_1}{Q_3+Q_1}=\frac{24-12}{24+12}=\frac{12}{36}\)
∴ चतुर्थक विचलन गुणांक = 0.33

⇒ औसत विचलन (MD) :
MD = \(\frac{\Sigma \mathrm{f}|\mathrm{X}-\overline{\mathrm{x}}|}{\mathrm{n}}=\frac{472.6}{80}\) = 5.906
∴ MD = 5.91
औसत विचलन गणांक = \(\frac{\mathrm{MD}}{\overline{\mathrm{x}}}=\frac{5.91}{18.05}\)
∴ औसत विचलन गुणांक = 0.33

प्रश्न 2.
निम्न दिये व्यापारियों के शाख के दिनों के आवृत्ति वितरण पर से कितने प्रतिशत अवलोकन \(\bar{X} \pm S\) की सीमा में समाविष्ट है वह ज्ञात कीजिए ।

उत्तर :
\(\bar{X} \pm S\) की सीमा में समाविष्ट अवलोकन की प्रतिशतता ज्ञात करने के लिए माध्य और प्रमाप विचलन ज्ञात करेंगे । इसके लिए निम्न सारणी बनायेंगे ।

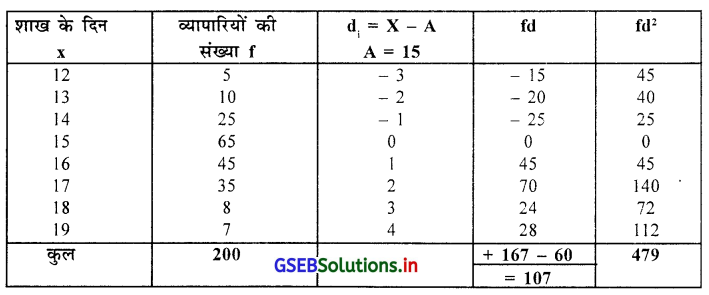
माध्य \(\bar{X}\) = A + \(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\)
15 + \(\frac{107}{200}\)
= 15 + 0.54
∴ \(\bar{X}\) = 15.4

प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fd}^2}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\right)^2}\)
= \(\sqrt{\frac{479}{200}-\left(\frac{107}{200}\right)^2}\)
= \(\sqrt{2.395-(0.54)^2}\)
= \(\sqrt{2.39-0.292}=\sqrt{2.0984}\)
= 1.449
∴ S = 1.45

अब \(\bar{x} \pm S\)
\(\bar{X}\) – S = 15.54 – 1.45 = 14.09
\(\bar{X}\) + S = 15.54 + 1.45 = 16.99

अब 14.09 से 16.99 के बीच के अवलोकन मूल्य 15, 16 है । उसके समक्ष की आवृत्ति 65 और 45 है अर्थात् \(\bar{x} \pm S\) में 65 + 45 = 110 है इसलिए \(\bar{x} \pm S\) के अंतराल में समाविष्ट अवलोकन के प्रतिशत
= \(\frac{110 \times 100}{200}\) = 55%

प्रश्न 3.
निम्न सूचना पर से अपकिरण का उचित माप ज्ञात करो और उसका सापेक्ष माप भी ज्ञात करो ।

उत्तर :
आवृत्ति वितरण खुला शिरावाला है इसलिए चतुर्थक विचलन योग्य माप है । चतुर्थक विचलन की गणना के लिए निम्नानुसार सारणी प्राप्त करेंगे ।

अंक	विद्यार्थियों की संख्या f	आवृत्ति संचयी cf
10 से कम	02	2
10 – 20	04	6
20 -30	10	16
30 – 40	03	19
40 से अधिक	01	20
कुल	20

प्रथम चतुर्थक Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{20}{4}\) = 5 वाँ अवलोकन के अनुरूप Q वर्ग = 10 – 20 है ।
∴ Q₁ = L + \(\frac{\frac{n}{4}-o f}{f}\) × C
जहाँ L = 10, \(\frac{n}{4}\) = 5, cf = 2, f = 4, c = 10
Q₁ = 10 + \(\frac{5-2}{4}\) × 10 = 10 + \(\frac{30}{4}\) = 10 + 7.5
∴ Q₁ = 17.5

तृतीय चतुर्थक Q₃ = 3(\(\frac{n}{4}\)) वाँ अवलोकन मूल्य
∴ = 3 (5) = 15 वाँ अवलोकन मूल्य cf की सारणी के अनुसार Q₃ वर्ग 20 – 30
Q₃ = L + \(\) × C
जहाँ L = 20, 3 (\(\frac{n}{4}\)) = 15, cf = 6, f = 10, c = 10
= 20 + \(\frac{15-6}{10}\) × 10 = 20 + 9
∴ Q₃ = 29
चतुर्थक विचलन Q _d = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{29-17.5}{2}\)
∴ Q_d = 5.75
चत्थक विचलन का सापक्ष माप = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{\mathrm{Q}_3+\mathrm{Q}_1}=\frac{29-17.5}{29+17.5}=\frac{11.5}{46.5}\)
∴ चतुर्थक विचलन का सापेक्ष माप = 0.25

प्रश्न 4.
एक कंपनी के 200 कर्मचारियों के वेतन की निम्न सूचना पर से कर्मचारियों के वेतन का प्रमाप विचलन ज्ञात कीजिए ।

उत्तर :
आवृत्ति वितरण ‘से कम’ प्रकार का दिया है उस पर से मूल आवृत्ति वितरण निम्नानुसार प्राप्त करेंगे । प्रमाप विचलन ज्ञात करना है । इसलिए माध्य की गणना की आवश्यकता नहि है । वर्गलम्बाई 10 और प्रथम वर्ग की उर्ध्वसीमा 10 है । इसलिए प्रथम वर्ग की अधःसीमा = 10 – 10 = 0 इसलिए प्रथम वर्ग 0 – 10 प्राप्त होगा। प्रत्येक वर्ग में वर्गलम्बाई जोड़ने से उर्ध्वसीमा और अधःसीमा प्राप्त होगी ।

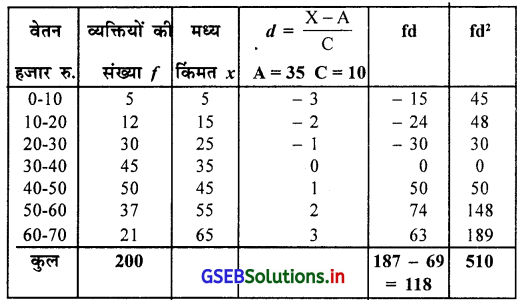
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fd}^2}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\right)^2}\) × c = \(\sqrt{\frac{510}{200}-\left(\frac{118}{200}\right)^2}\) × 10
= \(\sqrt{2.55-(0.59)^2}\) × 10 = \(\sqrt{2.55-0.3481}\) × 10
= \(\sqrt{2.2019}\) × 10 = 1.484 × 10
S = 14.84
∴ S = 14.84
कर्मचारियों के वेतन का प्रमाप विचलन 14.84 है ।

प्रश्न 5.
किसी एक दिन 100 लघुउद्योगों के शेयर का मूल्य (रु.) का वितरण निम्नानुसार है, तो शेयर के बंधमूल्य का औसत विचलन ज्ञात कीजिए।

उत्तर :

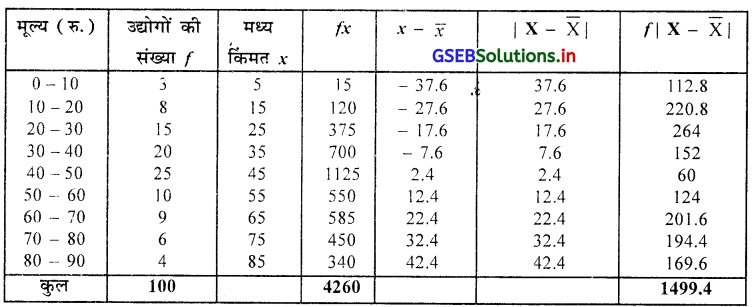
माध्य \(\overline{\mathrm{X}}=\frac{\sum f x}{n}=\frac{4260}{100}\)
∴ माध्य = 42.6
औसत विचलन MD = \(\frac{\sum f|X-\bar{X}|}{n}=\frac{\mid 499.4}{100}\)
∴ MD = 14.994
लघु उद्योगों के शेयर का औसत विचलन = 14.994 रु. है ।

प्रश्न 6.
किसी कारखाना के 230 कारीगरों को मिलती प्रतिदिन मजदूरी (रु. में ) की निम्न सूचना है । उस पर से सूचना का कारीगरों का दैनिक मजदूरी का विचरण गुणांक ज्ञात कीजिए ।

उत्तर :
आवृत्ति वितरण ‘से कम’ प्रकार का दिया है । इसलिये प्रथम मूल आवृत्ति प्राप्त करके माध्य और प्रमाप विचलन ज्ञात करेंगे ।

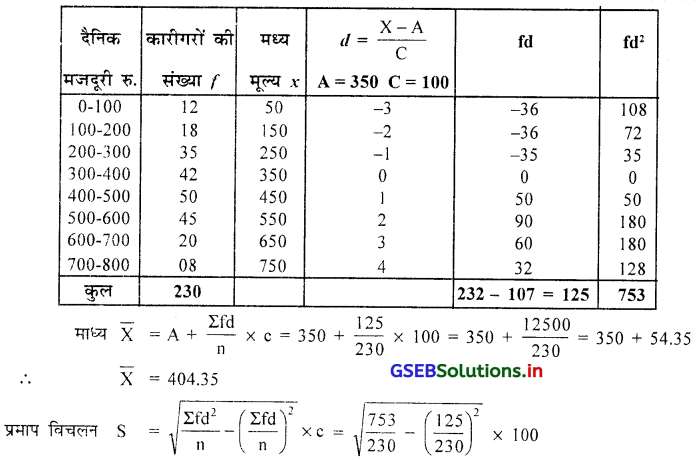
= \(\sqrt{3.274-(0.544)^2}\) × 100 = \(\sqrt{3.274-0.2959}\) × 100 = \(\sqrt{2.9781}\) × 100
= 1.7258 × 100
∴ S = 172.58 रु.
विचरण गुणांक :
\(\frac{S}{\bar{x}}\) × 100 = \(\frac{172.58}{404.35}\) × 100
∴ विचरण गुणांक = 42.68%

प्रश्न 7.
दो विद्यार्थी A और B द्वारा 10 परीक्षा में प्राप्त अंक निम्नानुसार है ।

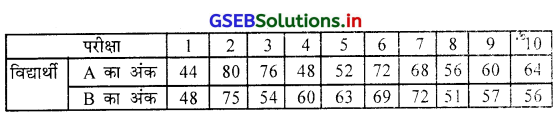
कौन से विद्यार्थी का अभ्यास में प्रदर्शन अधिक सुसंगत है ?
उत्तर :
दोनों विद्यार्थी की तुलना करने के लिए दोनों विद्यार्थी का विचरण ज्ञात करेंगे ।


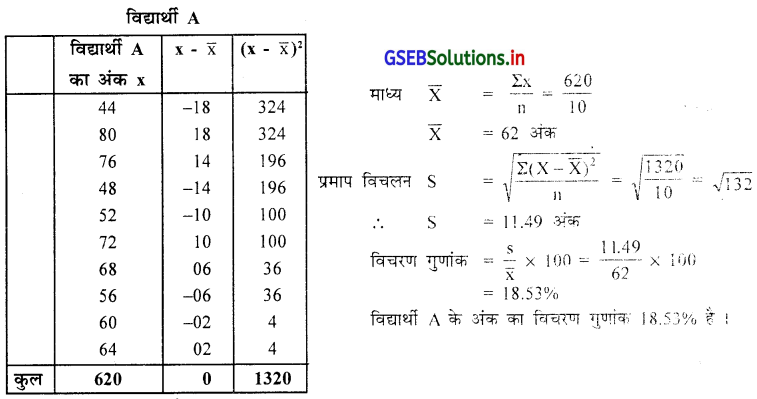
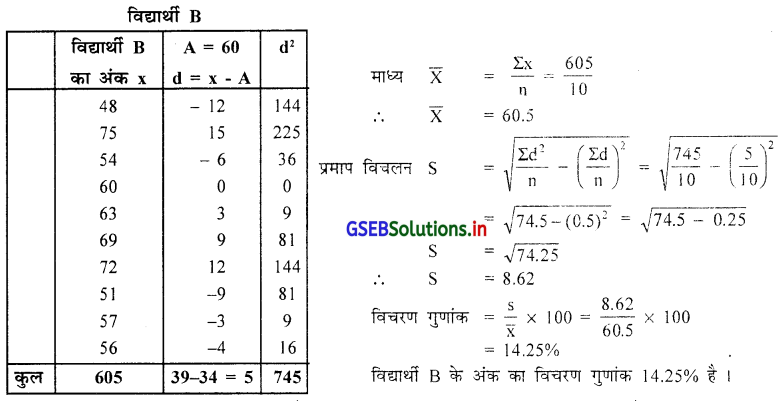
विद्यार्थी B का अंक का विचरण गुणांक कम है इसलिए विद्यार्थी B अभ्यास में अधिक सुसंगत है ।

प्रश्न 8.
दो समूह A और B के विद्यार्थियों के वजन (कि.ग्रा.) के आवृत्ति वितरण पर से दोनों समूह का विचरण गुणांक ज्ञात कीजिए । कौन-सा समूह में सापेक्ष चलन अधिक है ?

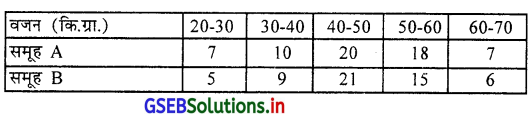
उत्तर :



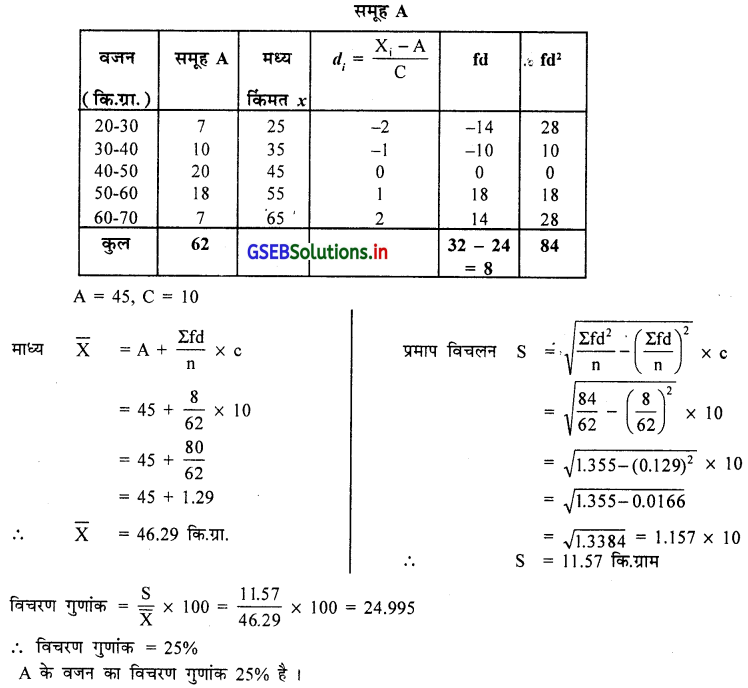
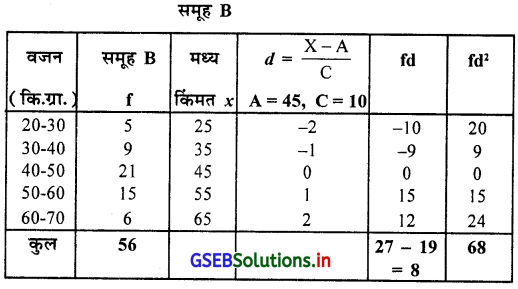
∴ समूह B का विचरण गुणांक = 23.54%
समूह A का विचरण गुणांक अधिक है इसलिए A में चलन अधिक है ।