Gujarat Board Statistics Class 11 GSEB Solutions Chapter 5 आवृत्ति वितरण की विषमता Ex 5.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 5 आवृत्ति वितरण की विषमता Ex 5.1
प्रश्न 1.
निम्नलिखित आवृत्ति वितरण 59 ग्राहकों द्वारा 500 मिलि. पेश्च्युराईझ टोन्ड दूध की थैलिओं की मात्रा की माँग के अनुरूप है । कार्ल पियर्सन की विधि से वैषम्यांक ज्ञात करो ।

उत्तर :
यहा आवृत्ति वितरण एक भूयिष्ठकवाला है इसलिए कार्यपियर्सन का वैषम्यांक ज्ञात करने के लिए माध्य भूयिष्ठक और प्रमाप विचलन की गणना करेंगे ।
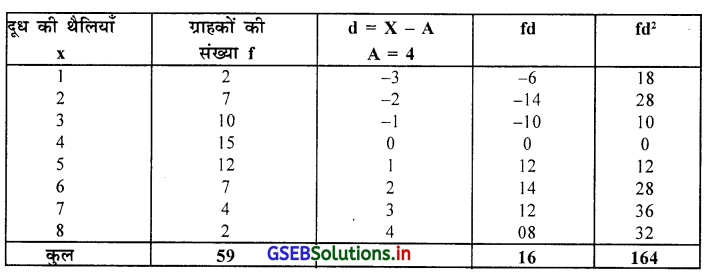
माध्य \(\bar{X}\) = A + \(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\)
= 4 + \(\frac{16}{59}\)
= 4 + 0.27
∴ \(\bar{X}\) = 4.27 इकाई
भूयिष्ठक MO = महत्तम आवृत्ति 15 के अनुरूप अवलोकन 4 है।
∴ Mo = 4 इकाई

![]()
प्रश्न 2.
निम्न आवृत्ति वितरण 270 ग्राहक द्वारा टी.शर्ट के भिन्न भिन्न कंधों की लम्बाई (ईच में) के आधार से खरीदी का है । उस सूचना का उपयोग करके कार्लपियर्सन की पद्धति से वैषम्यांक ज्ञात करो और उसका अर्थघटन करो ।

उत्तर :
यहाँ आवृत्ति वितरण में महत्तम आवृत्ति दो है इस लिए दो भूयिष्ठक होने से विषमतांक ज्ञात करने के लिए माध्य, मध्यका और प्रमाप विचलन की गणना करेंगे ।
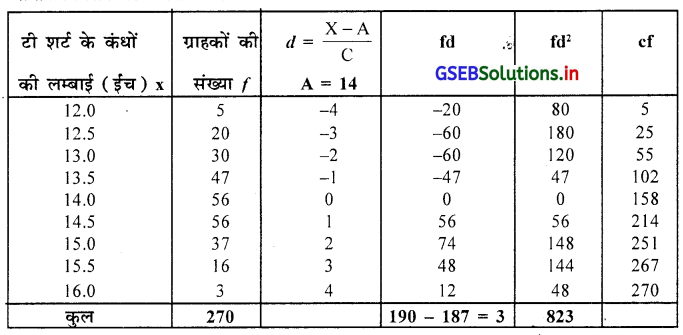

∴ j = 0.03
विषमतांक का माप 0 के समीप है इसलिए आवृत्ति वितरण संममितियता के अधिक समीप है ।
प्रश्न 3.
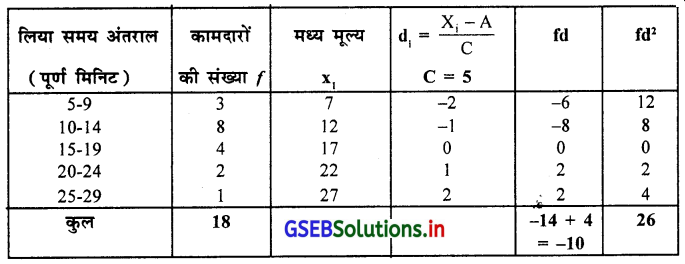
एक कार्य को पूर्ण करने के लिए प्रत्येक कामदार द्वारा लगा समय निम्न आवृत्ति वितरण द्वारा प्राप्त किया गया है ।
इस सूचना पर से कार्लपियर्सन की पद्धति से विषमतांक ज्ञात करके उसका अर्थघटन करो ।

उत्तर :
यहाँ आवृत्ति वितरण एक भूयिष्ठकवाला है इसलिए कार्लपियर्सन का वैषम्यांक ज्ञात करने के लिए माध्य, भूयिष्ठक और प्रमाप विचलन ज्ञात करेंगे ।
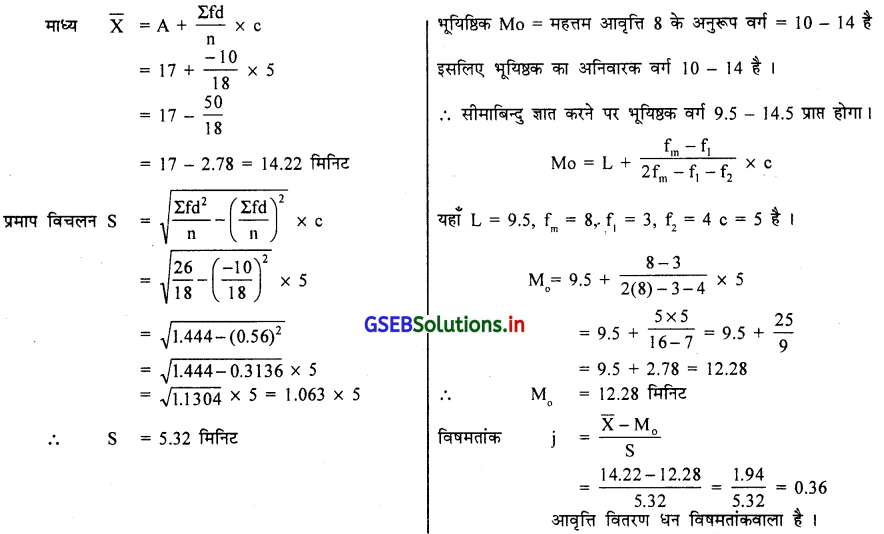
![]()
प्रश्न 4.
कक्षा 11 के विद्यार्थियों द्वारा आई.टी. कंपनीओं के लाभ (करोड़ रुपिया में ) की निम्नलिखित सूचना एकत्रित की है। उस पर से कार्लपियर्सन की पद्धति से वैषम्यांक ज्ञात करो और उसका अर्थघटन करो ।

उत्तर :
यहाँ आवृत्ति वितरण एक भूयिष्ठकवाला है इसलिए कार्लपियर्सन का वैषम्यांक ज्ञात करने के लिए माध्य, भूयिष्ठक और प्रमाप । विचलन ज्ञात करेंगे ।
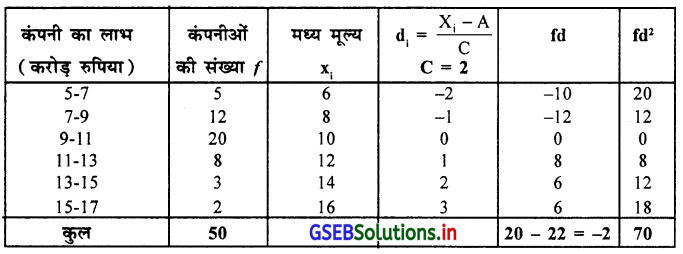

∴ j = 0.05
विषमतांक का माप 0 के समीप है इसलिए आवृत्ति वितरण संमित है ।
प्रश्न 5.
निम्न आवृत्ति वितरण 38 कंपनियों के वार्षिक घिसाई की रकम (लाख रुपिया में) के अनुसार है । इस सूचना का उपयोग करके कार्लपियर्सन की पद्धति से विषमता और विषमतांक ज्ञात करो । विषमता का प्रकार बताइए ।

उत्तर :
दिया गया आवृत्ति वितरण मिश्र प्रकार का है । इसलिए माध्य, मध्यका और प्रमाप विचलन की गणना करेंगे ।
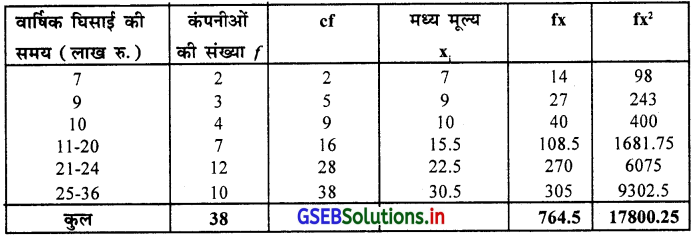
माध्य \(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{fx}}{\mathrm{n}}=\frac{764.5}{38}\)
∴ = \(\overline{\mathrm{X}}\) = 20.12 लाख
मध्यका M = \(\frac{\mathrm{n}}{2}\) वाँ अवलोकन मूल्य cf के कोष्टक में देखने पर
= \(\frac{38}{2}\) = 19 वाँ अवलोकन मूल्य
∴ M वर्ग = 21 – 24 वर्ग अनिवारक है इसलिए सीमाबिन्दु प्राप्त करने पर M वर्ग 20.5 – 24.5
M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
जहाँ L = 20.5, \(\frac{n}{2}\) = 19, cf = 16, f = 12, c = 4
M = 20.5 + \(\frac{19-16}{12}\) × 4 – 20.5 + \(\frac{3 \times 4}{12}\) = 20.5 + 1
∴ M = 21.5 लाख
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fx}^2}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{fx}}{\mathrm{n}}\right)^2}\) अथवा \(\sqrt{\frac{\Sigma f^2}{n}-(\bar{X})^2}\)
= \(\sqrt{\frac{1780025}{38}-(20.12)^2}\) = \(\sqrt{468.428-404.814}=\sqrt{63.614}\)
∴ S = 7.98 लाख
विषमता SK = 3 (\(\bar{X}\) – M) = 3 (20.12 – 21.5) = 3 (-1.38)
∴ SK = – 4.14
विषमतांक j = \(\frac{3(\bar{X}-M)}{S}=\frac{3(20.12-21.5)}{7.98}=\frac{-4.14}{7.98}\)
∴ j = – 0.52 दिया गया आवृत्ति वितरण में ऋण विषमता है ।
![]()
प्रश्न 6.
कपड़ा बनानेवाली 35 मिलों में एक माह दौरान रुई का उपयोग निम्नानुसार है । उस पर से कार्लपियर्सन की विधि से विषमता और विषमतांक ज्ञात करके विषमता का प्रकार बताइए ।

उत्तर :
आवृत्ति वितरण में वर्गलम्बाई असमान है । इसलिए भूयिष्ठक ज्ञात नहि होगा । इसलिए माध्य, मध्यका और प्रमाप विचलन का उपयोग करेंगे ।
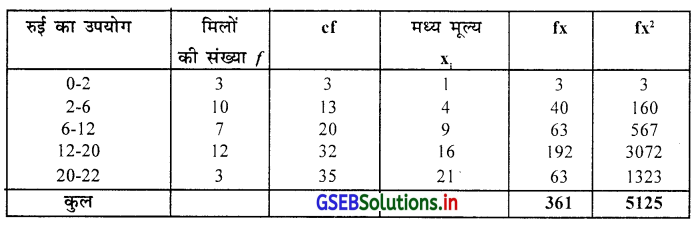
माध्य \(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{fx}}{\mathrm{n}}=\frac{361}{35}\)
∴ \(\overline{\mathrm{X}}\) = 10.31 हजार गांठ
मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य cf के कोष्टक में देखने पर
= \(\frac{35}{2}\) = 17.5 वाँ अवलोकन मूल्य
∴ M वर्ग = 6-12
M = L + \(\frac{\frac{11}{2}-\mathrm{cf}}{f}\) × c
जहाँ L = 6, \(\frac{\mathrm{n}}{2}\) = 17.5, cf = 13, f = 7, c = 6
M = 6 + \(\frac{17.5-13}{7}\) × 6 = 6 + \(\frac{27}{7}\) = 6 + 3.86
∴ M = 9.86 हजार गांठ
प्रमाप बिचलन S = \(\sqrt{\frac{\Sigma f x^2}{n}-\left(\frac{\sum f x}{n}\right)^2}\) = \(\sqrt{\frac{5125}{35}-\left(\frac{361}{35}\right)^2}\)
= \(\sqrt{146.429-(10.31)^2}\) = \(\sqrt{146.429-106.296}=\sqrt{40.133}\)
S = 6.335
∴ S = 6.34 हजार गांठ
विषमता SK = 3 (\(\bar{x}\) – M) = 3 (10.31 – 9.86) = 3 (0.45)
विषमतांक j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}=\frac{3(10.31-9.86)}{6.34}\) = \(\frac{3(0.45)}{6.34}=\frac{1.35}{6.34}\)
∴ j = 0.21 दिया गया आवृत्ति वितरण में धन विषमता है ।
![]()
प्रश्न 7.
पर्यटन के एक स्थान का वर्ष 2014 के 60 दिनों का तापमान सेल्सियस में निम्नानुसार है । इस सूचना का उपयोग करके कार्ल पियर्सन की विधि से विषमता और विषमतांक ज्ञात करो । विषमता का प्रकार बताइए ।

उत्तर :
आवृत्ति वितरण में वर्गलम्बाई असमान है इसलिए भूयिष्ठक ज्ञात नहि होगा । अतः माध्य, मध्यका और प्रमाप विचलन की गणना करेंगे ।
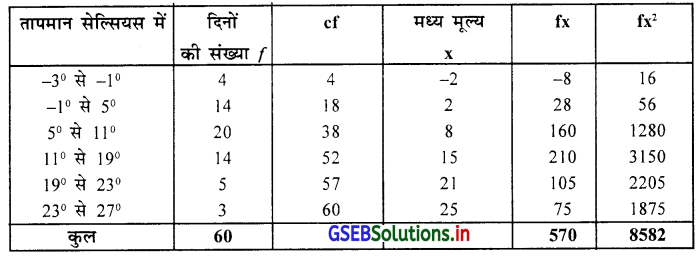
माध्य \(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{fx}}{\mathrm{n}}=\frac{570}{60}\) = 9.5 सेल्सियस
मध्यका M = \(\frac{\mathrm{n}}{2}\) वाँ अवलोकन मूल्य
= \(\frac{\mathrm{60}}{2}\) = 30 वाँ अवलोकन मूल्य cf के कोष्टक में देखने पर M वर्ग 50 से 11° प्राप्त होगा ।
M = L + \(\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\) x c
जहाँ L = 5, \(\frac{\mathrm{n}}{2}\) = 30, cf = 18, f = 20, c = 6
M = 5 + \(\frac{30-18}{20}\) x 6 = 5 + \(\frac{72}{20}\) = 5 + 3.6
:: M = 8.6 सेल्सियस
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fx}}{\mathrm{n}}-(\overline{\mathrm{X}})^2}=\sqrt{\frac{8582}{60}-(9.5)^2}\) = \(\sqrt{143.033-90.25}=\sqrt{52.783}\)
s = 7.27 सेल्सियस विषमता
SK = 3 (\(\bar{x}\) – M) = 3 (9.5 – 8.6) = 3 (0.9)
= 2.7
विषमताक j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}=\frac{3(9.5-8.6)}{7.27}\) = \(\frac{3(0.9)}{7.27}=\frac{2.7}{7.27}\)
= 0.37 आवृत्ति वितरण में धन विषमता है ।