GSEB Solutions Class 11 Statistics Chapter 5 Skewness of Frequency Distribution Ex 5.2

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 5 Skewness of Frequency Distribution Ex 5.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 5 Skewness of Frequency Distribution Ex 5.2

Question 1.
From the following frequency distribution of different youngsters exercising in a gymnasium, find coefficient of skewness by Bowley’s method and state the type of skewness:

Answer:
We arrange the observallon of age in ascending order.

First Quartile:
Q₁ = value of \(\left(\frac{n+1}{4}\right)\)th observation
= value of \(\left(\frac{83+1}{4}\right)\)th observation
= value of 21 th observation

Referring to column cf. Q₁ = 20 years

Median:
M = value of \(\left(\frac{n+1}{2}\right)\)th observation
= value of \(\left(\frac{83+1}{2}\right)\)th observation
= value of 42th observation
Referring to column cf, M = 22 years

Third Quartile:
Q₃ = value of 3\(\left(\frac{n+1}{4}\right)\) th observation
= value of 3 (21)th observation
= value of 63rd observation

Referring to column cf, Q₃= 25 years

Coefficient of skewness by Bowley’s Method:

Type of skewness:
j = 0.2. Therefore, the given distribution is positively skewed.

Question 2.
The frequency distribution of paid up share capital out of the issued share capital for 31 manufacturing companies is as follows. Find skewness and its coefficient by Bowley’s method and state the type of skewness.

Answer:
The given frequency distribution is ‘less than’ type cumulative frequency distribution. The difference between two successive, upper boundary points is 200. Therefore class length c = 20. We calculate coefficient of skewness by Bowley’s method obtaining original frequency distribution.

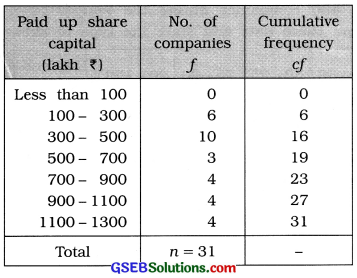
First Quartile:
Q₁ class = class that includes \(\frac{n}{4}\)th observation
= class that includes \(\frac{31}{4}\)th observation
= class that includes 7.75th observation

Referring to column cf,
Q₁ class = 300 – 500
Now, Q₁ = L + \(\frac{\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 300, \(\frac{n}{4}\) = 7.75, cf = 6, f = 10 and c = 200 in the formula,
Q1 = 300 + \(\frac{7.75-6}{10}\) × 200
= 300 + (1.75 × 20)
= 300 + 35
= ₹ 335 lakh

Median:
M class = class that includes \(\left(\frac{n}{2}\right)\)th observation
= class that includes \(\left(\frac{31}{2}\right)\)th observation
= class that includes 15.5th observation

Referring to column cf, M Class = 300 – 500
Now, M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
Putting L = 300, \(\frac{n}{2}\) = 15.5, cf = 6, f = 10 and c = 200 in the formula,
M = 300 + \(\frac{15.5-6}{10}\) × 200
= 300 + (9.5 × 20)
=300 + 190 = ₹ 490 lakh

Third Quartile :
Q₃ class = class that includes 3\(\left(\frac{n}{4}\right)\)th observation
= class that includes 3 (7.75) th observation
= class that includes 23.25 th observation

Referring to column cf, Q₃ class = 900 – 1100
Now, Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 900, 3\(\left(\frac{n}{4}\right)\) = 23,25, cf = 23, f = 4 and c = 200 in the formula,
Q₃ = 900 + \(\frac{23.25-23}{4}\) × 200
= 900 + (0.25 × 50)
= 900 + 12.5
= ₹ 912.5 lakh

Bowley’s method :
Skewness :
S_k = Q₃ + Q₁ -2M
= 912.5 + 335 – 2(490)
= 1247.5 – 980
= ₹ 267.5 lakh

Coefficient of skewness :
j = \(\frac{\mathrm{Q}_{3}+\mathrm{Q}_{1}-2 \mathrm{M}}{\mathrm{Q}_{3}-\mathrm{Q}_{1}}\)
= \(\frac{{S}_{k}}{Q_{3}-Q_{1}}\)
= \(\frac{267.5}{912.5-335}=\frac{267.5}{577.5}\) = 0.46

Type of skewness :
j = 0.46. Therefore, frequency distribution is positively skewed.

Question 3.
The distribution of sales (In thousand tons) of 400 companIes during the year 2014 – 15 Is as follows. Find skewness and its coefficient from these data and state the type of skewness.

Answer:

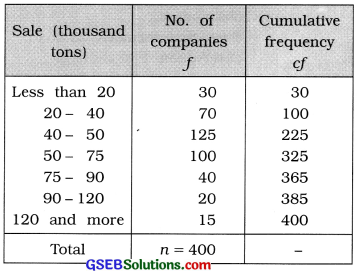
First Quartile:
Q₁ class = class that includes \(\frac{n}{4}\)th observation
= class that includes \(\frac{400}{4}\)th observation
= class that includes 100th observation

Referring to column cf,
Q₁ class = 20 – 40
Now, Q₁ = L + \(\frac{\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 20, \(\frac{n}{4}\) = 100, cf = 30, f = 70 and c = 20 in the formula,
Q₁ = 20 + \(\frac{100-30}{10}\) × 20
= 20 + \(\frac{70 \times 20}{70}\)
= 20 + 20
= 40 thousand tons

Median:
M class = class that includes \(\left(\frac{n}{2}\right)\)th observation
= class that includes \(\left(\frac{400}{2}\right)\)th observation
= class that includes 200th observation

Referring to column cf, M Class = 40 – 50
Now, M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
Putting L = 40, \(\frac{n}{2}\) = 200, cf = 100, f = 125 and c = 10 in the formula,
M = 40 + \(\frac{200-100}{125}\) × 10
= 40 + \(\frac{100 \times 10}{125}\)
= 40 + 8 = 48 thousand tons

Third Quartile :
Q₃ class = class that includes 3\(\left(\frac{n}{4}\right)\)th observation
= class that includes 3 (100) th observation
= class that includes 300 th observation

Referring to column cf, Q₃ class = 50 – 75
Now, Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 50, 3\(\left(\frac{n}{4}\right)\) = 300, cf = 225, f = 100 and c = 205 in the formula,
Q₃ = 50 + \(\frac{23.25-23}{4}\) × 200
= 50 + \(\frac{300 \times 225}{100}\) × 25
= 50 + 18.75
= 68.75 thousand tons

Bowley’s method :
Skewness :
S_k = Q₃ + Q₁ -2M
= 68.75 + 40 – 2(48)
= 108.75 – 96
= 12.75 thousand tons

Coefficient of skewness :
j = \(\frac{\mathrm{Q}_{3}+\mathrm{Q}_{1}-2 \mathrm{M}}{\mathrm{Q}_{3}-\mathrm{Q}_{1}}\)
= \(\frac{{S}_{k}}{Q_{3}-Q_{1}}\)
= \(\frac{12.75}{68.75-40}=\frac{12.75}{28.75}\) = 0.44

Type of skewness :
j = 0.44. Therefore, frequency distribution is positively skewed.

Question 4.
The commission paid on insurance policy amount to agents in a branch of an Insurance company during a month has the following frequency distribution. Find the coefficient of skewness by Bowley’s method.

Answer:

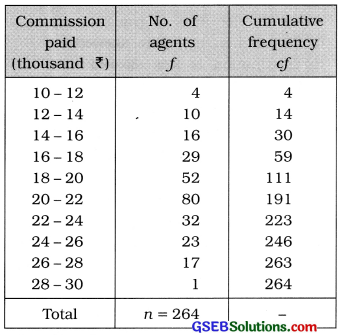
First Quartile:
Q₁ class = class that includes \(\frac{n}{4}\)th observation
= class that includes \(\frac{264}{4}\)th observation
= class that includes 66th observation

Referring to column cf,
Q₁ class = 18 – 20
Now, Q₁ = L + \(\frac{\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 20, \(\frac{n}{4}\) = 100, cf = 59, f = 52 and c = 2 in the formula,
Q₁ = 18 + \(\frac{66-59}{52}\) × 2
= 18 + \(\frac{7 \times 2}{52}\)
= 18 + \(\frac{14}{52}\)
= 18 + 0.27
= ₹ 18.27 thousand

Median:
M class = class that includes \(\left(\frac{n}{2}\right)\)th observation
= class that includes \(\left(\frac{264}{2}\right)\)th observation
= class that includes 200th observation

Referring to column cf, M Class = 20 – 22
Now, M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
Putting L = 20, \(\frac{n}{2}\) = 132, cf = 111, f = 80 and c = 2 in the formula,
M = 20 + \(\frac{132-111}{80}\) × 2
= 20 + \(\frac{100 \times 10}{125}\)
= 20 + \(\frac{21}{40}\)
= 20 + 0.53
= ₹ 20.53 thousand

Third Quartile :
Q₃ class = class that includes 3\(\left(\frac{n}{4}\right)\)th observation
= class that includes 3 (66) th observation
= class that includes 198 th observation

Referring to column cf, Q₃ class = 22 – 24
Now, Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 22, 3\(\left(\frac{n}{4}\right)\) = 198, cf = 191, f = 32 and c = 2 in the formula,
Q₃ = 22 + \(\frac{198-191}{32}\) × 2
= 22 + \(\frac{7}{16}\) × 25
= 22 + 0.44
= ₹ 22.44 thousand

Bowley’s method :
Coefficient of skewness :
j = \(\frac{\mathrm{Q}_{3}+\mathrm{Q}_{1}-2 \mathrm{M}}{\mathrm{Q}_{3}-\mathrm{Q}_{1}}\)
= \(\frac{{S}_{k}}{Q_{3}-Q_{1}}\)
= \(\frac{22.44+18.27-2(20.53)}{22.44-18.27}\)
= \(\frac{40.71-41.06}{4.17}=\frac{-0.35}{4.17}\)
= -0.08