Gujarat Board Statistics Class 11 GSEB Solutions Chapter 6 Permutations, Combinations and Binomial Expansion Ex 6.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 6 Permutations, Combinations and Binomial Expansion Ex 6.3
Question 1.
Obtain the expansion of the following binomial expressions:
(1) (3a + 4b)3
Answer:
(3a + 4b)3 = 3C0 (3a)3 (4b)0 + 3C1 (3a)2 (4b)1 + 3C2 (3a) (4b)2 + 3C3 (3a)0 (4b)3
= 1 . 27a3. 1 + 3 . 9a2 . 4b + 3 . 3a . 16b2 + 1 . 1 . 64b3
= 27a3 + 108a2b + 144b2 + 64b3
(2) (1 + x)7
Answer:
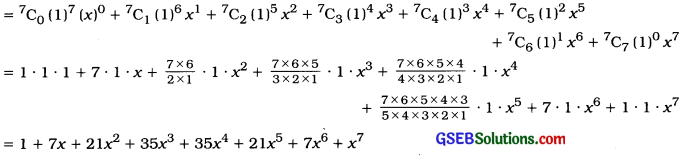
(3) \(\left(\frac{3}{x}-\frac{4 x}{3}\right)^{4}\)
Answer:

(4) \(\left(\frac{\sqrt{x}}{3}+\frac{3}{\sqrt{x}}\right)^{6}\)
Answer:

(5) \(\left(\frac{a}{2}-\frac{b}{3}\right)^{5}\)
Answer:

![]()
Question 2.
Obtain the values using binomial expansion:
(1) (√5 +1)5 – (√5 – 1)5
Answer:

(2)(√2 + 1)6 + (√2 – 1)6
Answer:

(3) (√5 + √3)4 + (√5 – √3)4
Answer:

Question 3.
Expand (1 + x)5 and verify by putting x = 1 on both sides.
Answer:
(1 + x)5 = 5C0 . 1 . x0 + 5C1 . 1 . x1 + 5C2 1 x2 + 5C3 . 1 . x3 + 5C4 1 x4 + 5C5 . 1 . x5
= 1+ 5x + 10x2 + 10x3 + 5x4 + x5
LHS = (1 + x)5
Putting x = 1,
LHS = (1 + 1)5 = (2)5 = 32
RHS = 1 + 5x + 10x2 + 10x3 + 5x4 + 1
Putting x = 1.
RHS= 1 +5(1)+ 10(1)2+ 10(1)3 + 5(1)4 + 15
= 1 + 5 + 10 + 10 + 5 + 1 = 32
Hence, LHS = RHS
![]()
Question 4.
Expand (1 + a)6 and verify by putting a = 2 on both sides.
Answer:
(1 + a)6 = 6C0 1 a0 + 6C1 . 1 . a1 + 6C2 . 1 . a2 + 6C3 . 1 . a3 + 6C4. 1 .a4 + 6C5 . 1 . a5 + 6C6 1 . a6
= 1 + 6a + 15a2 + 20a3 + 15a4 + 6a5 + a6
LHS = (1 + a)6
Putting a = 2.
LHS = (1 + 2)6 = (3)6 = 729
RHS = 1 + 6a + 15a2 + 20a3 + 15a4 + 6a5 + a6
Putting a = 2.
RHS= 1 + 6 × 2 + 15(2)2 + 20(2)3 + 15(2)4 + 6(2)5 + (2)6
= 1 + 12 +(15 × 4) + (20 × 8) + (15 × 16) + 6(32) + 64
= 13 + 60 + 160 + 240 + 192 + 64
= 729
Hence, LHS = RHS