Gujarat Board Statistics Class 11 GSEB Solutions Chapter 6 क्रमचय, संचय और द्विपद विस्तार Ex 6.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 6 क्रमचय, संचय और द्विपद विस्तार Ex 6.3
प्रश्न 1.
निम्न द्विपद पदावलि का विस्तार कीजिए ।
(1) (3a + 4b)3
(2) (1 + x)7
(3) (\(\frac{3}{x}-\frac{4 x}{3}\))4
(4) (\(\frac{\sqrt{x}}{3}+\frac{3}{\sqrt{x}}\))4
(5) (\(\frac{a}{2}-\frac{b}{3}\))5
उत्तर :
(1) (3a + 4b)3 = 3C0 (3a)3 + 3C1 (3a)2 (4b) + 3C2 (3a)1 (4b)2 + 3C3 (4b)3
= 1 × 27a3 + 3 × 9a2 × 4b + 3 × 3a × 16b2 + 1 × 64b3
= 27a3 + 108a2b + 144ab2 + 64b3
(2) (1 + x)7 = 7C0 (1)7 + 7C1 (1)6 (x) + 7C2 (1)5 (x2) + 7C3 (1)4 (x)3 + 7C4 (1)3 (X4) + 7C5 (1)2 (x5)
7C6 (1) (x6) + 7C7 (x7)
= 1 × 1 + 7 × 1 × x + 21 × 1 × x2 + 35 × 1 × x3 + 35 × 1 × x4 + 21 × 1 × x5 7 × 1 × x2 + 1 × x7
= 1 + 7x + 21x2 + 35x3 + 35x4 + 21x5 + 7x6 + x7
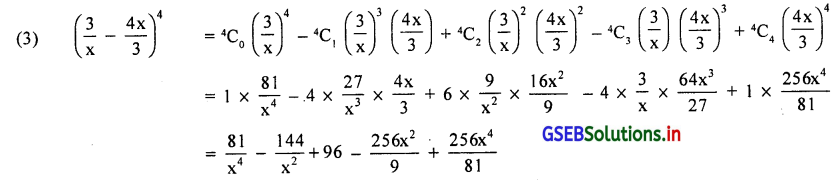

![]()
प्रश्न 2.
द्विपद विस्तार के उपयोग द्वारा मूल्य की प्राप्ति कीजिए ।
(1) (√5 + 1)5 – (√5 – 1)5
(2) (√2 + 1)6 + (√2 – 1)6
(3) (√5 + √3)4 + (√5 – √3)4
उत्तर :
(1) (√5 + 1)5 – (√5 – 1)5

(दो द्विपद पदावलि के बीच ऋण चिन्ह होने से दूसरी पदावलि के चिन्ह में परिवर्तन होगा जिससे दोनों पदावलि में प्रथम, तृतीय और पाचवा पद का लोप होगा ।)
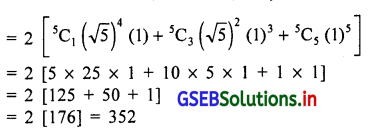
(2) (√2 + 1)6 + (√2 – 1)6

(दो द्विपद पदावलि के बीच धण चिन्ह होने से दूसरी पदावलि के चिन्ह में परिवर्तन नहीं होगा । परिणामस्वरूप दोनों पदावलि में दूसरा, चौथा और छठ्ठा पद का लोप होगा ।)
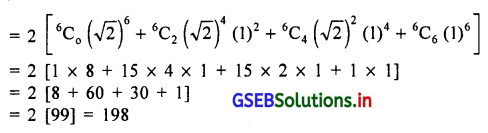
(3) (√5 + √3)4 + (√5 – √3)4

(अब दो पदावलि के बीच धन चिन्ह होने से दूसरी पदावलि के चिन्ह में परिवर्तन नहि होगा । परिणामस्वरूप दोनों पदावलि का दूसरा और चौथा पद का लोप होगा ।)
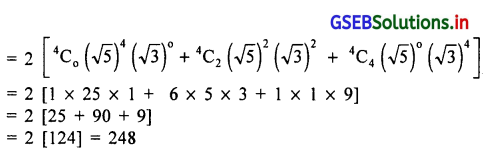
प्रश्न 3.
(1 + x)5 का विस्तार करो और दोनों और x = 1 रखके जाँच करो ।
उत्तर :
(1 + x)5 = 5C0 (1)5 (x)0 + 5C1 (1)4 (x)1 + 5C2 (1)3 (x)2 + 5C3 (1)2 (x)3 + 5C4 (1)1 (x)4 + 5C5 (1)0 (x)5
= 1 × 1 × 1 + 5 × 1 × x + 10 × 1 × x2 + 10 × 1 × x3 + 5 × 1 × x4 + 1 × 1 × x5
= 1 + 5x + 10x2 + 10x3 + 5x4 + x5
x = 1 रखने पर
L.H.S. = (1 + x)5 = (1 + 1)5 = (2)5 = 32
R.H.S. = 1 + 5x + 10x2 + 10x3 + 5x4 + x5
= 1 + 5(1) + 10(1)2 + 10(1)3 + 5(1)4 + (1)5
= 1 + 5 + 10 + 10 + 5 + 1 = 32
इसलिए L.H.S. = R.H.S.
![]()
प्रश्न 4.
(1 + a)6 का विस्तार करो और दोनों और a = 2 रखकर जाँच करो ।
उत्तर :
(1 + a)6 = 6C0 (1)6 (a)0 + 6C1 (1)5 (a)1 + 6C2 (1)4 (a)2 + 6C3 (1)3 (a)3 + 6C4 (1)2 (a)4 + 6C5 (1)1 (a)5 +
6C5 (1)0 (a)6
= 1 × 1 × 1 + 6 × 1 × a + 15 × 1 × a2 + 20 × 1 × a3+ 15 × 1 × a4 + 6 × 1 × a5 + 1 × 1 × a6
= 1 + 6a + 15a2 + 20a3 + 15a4 + 6a5 + a6
a = 2 रखने पर
LHS = (1 + a)6 = (1 + 2)6 = (3)6 = 729
RHS = 1 + 6a + 15a2 + 20a3 + 15a4 + 6a5 + a6
= 1 + 6 × 2 + 15 × (2)2 + 20 (2)3 + 15 (2)4 + 6 (2)5 + (2)6
= 1 + 12 + 60 + 20 × 8 + 15 × 16 + 6 × 32 + 64
= 1 + 12 + 60 + 160 + 240 + 192 + 64
= 729
इसलिए LHS = RHS