Gujarat Board Statistics Class 11 GSEB Solutions Chapter 8 Function Ex 8 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 8 Function Ex 8
Section – A
Choose the correct option from those given below each question:
Question 1.
Which of the following statement is true?
(a) f: {1, 2, 3, 4} → {3, 4, 5}, the rule ‘add 2 to the elements of domain’ is not a function.
(b) f: A → B, A = {-2, -1, 0, 1, 2}; B = {0, 1, 2, 3, 4}; f(x) = x2 is not a function.
(c) g : P → Q, P = {-1, 0, 1}; Q = {-\(\frac{1}{3}\), -1, 3}; g (x) = \(\frac{x+2}{x-2}\). then g is called function.
(d) g : {2, 3, 4, 5} → {-1, 0, 1) and g(x) = 4x – 3 is a function.
Answer:
(a) f: {1, 2, 3, 4} → {3, 4, 5}, the rule ‘add 2 to the elements of domain’ is not a function.
Question 2.
Which of the following statements is true for the range of function f: A B?
(a) f(A) = {f(x)|x ∈ A}
(b) It is not a co-domain or subset of co-domain.
(c) Domain itself is the range
(d) f(A) = {f(x) | x ∈ B}
Answer:
(a) f(A) = {f(x)|x ∈ A}
Question 3.
Which of the following statements is true for the relation g : X → Y, X = {- 1, 0}; Y = {2, 4}; g (x) = 4 – 2x ?
(a) g is called a function.
(b) g is not a function.
(c) X is called function.
(d) Y is called function.
Answer:
(b) g is not a function
Question 4.
What is the type of function f: A → B, wherein, for two different values of domain their functional values are same?
(a) One-one function
(b) Many-one function
(c) One-many function
(d) Many-many function
Answer:
(b) Many-one function
Question 5.
What is the type of function f: A → B, where each value of domain A has the same image in set B?
(a) Not a function
(b) One-one function
(c) Constant function
(d) Many-one function
Answer:
(c) Constant function
![]()
Question 6.
Which of the following statements is true for a one-one function?
(a) Only for two values of the domain, their images should be different.
(b) For any two values of the domain, their images are same.
(c) For any two different values of the domain, their images are different.
(d) For each value of the domain, their images are same.
Answer:
(c) For any two different values of the domain their images are different.
Question 7.
What is the type of function f: Z – {0} → N and f(x) = x2, x ∈ Z-{0}?
(a) One-one function
(b) Many-one function
(c) Constant function
(d) None of the given
Answer:
(b) Many-one function
Question 8.
Which of the following is a sufficient condition for two different functions to be equal?
(a) Domains of both the functions must be same.
(b) Ranges of both the functions must be same.
(c) (a) and (b)
(d) (a) or (b)
Answer:
(c) (a) and (b)
Section – B
Answer the following questions in one sentence:
Question 1.
Give the necessary condition for defining a function.
Answer:
The necessary condition for defining a function is that ‘domain and co-domain of the function should not be empty sets.’
Question 2.
f: A → B, A = {-3, -1, 1, 3};
B = {1, 0, 9}; f(x) = x2. Is f a function?
Answer:
f: A → B, A = {- 3, -1, 1, 3};
B = {1, 0, 9}; f(x) = x2. Therefore, f is a function.
Question 3.
g: N → N, ‘subtract 2 from the elements of the domain’. Can this rule be called a function?
Answer:
g : N → N, i.e., N = {1, 2, 3, …};
N = {1, 2, 3,…}. Therefore, ‘subtract 2 from the elements of the domain’ this rule cannot be called a function.
Question 4.
Define a one-one function in notations.
Answer:
Suppose, f: A → B. If for any two different elements x1 and x2. f(x1) ≠ f(x2), then function f is called one-one function.
Question 5.
Define many-one function in notations.
Answer:
Suppose, f: A → B. If for any two differents x1, x2 of domain A. f(x1) = f(x2), then function / is called many-one function.
Question 6.
Define constant function in notations.
Answer:
Suppose, f: A → B. If for each element x1, x2, x3,… of domain, the image is same in co-domain B, i.e.„ f(x1) = f(x2) = f(x3) = … then, function f is called constantant function.
Question 7.
f: {1, 2, 3} → N, g : {2, 3, 4} → N,
f (x) = 2x + 1 and g (x) = x – 1. Can these two functions f and g be equal functions? Why?
Answer:
f:{1, 2, 3} → N and g:{2, 3, 4} → 1. Domain of f and g are not equal. Therefore, f and g are not equal functions.
Question 8.
f : Z → N, f(t) = t2 + 1, t ∈ Z. Determine the type of function f.
Answer:
f: Z → N.
∴ Z = {…-3,-2, -1, 0, 1, 2, 3,…} and N = {1, 2, 3, 4, …}
f(t) = t2 + 1, t ∈ Z
∴ f(- 3) = 9 + 1 = 10, f(3) = 9 + 1 = 10, f(- 2) = 4 + 1 = 5 f(2) = 4 + 1 = 5
Here, for two different elements of domain A, their images are same in co-domain. Therefore, function / is many-one function.
Question 9.
f: N → N, f(t) = t2 + 1, t ∈ N. Determine the type of function f.
Answer:
f: N → N. ∴ N = {1, 2, 3, 4,…} and
N = {1, 2, 3, 4, …}
f(t) = t2 + 1, t ∈ N
f(1)= 1 + 1 = 2,
f(2) = 22 + 1 = 5
Here, for two different elements of do-main
A, their images are different in co-domain. Therefore, function f is one-one function.
Question 10.
Define a function of real variable.
Answer:
If f: A → B. where AcR then f is called a function of real variable.
Section – C
Answer the following questions as required:
Question 1.
Give definition of a function.
Answer:If A and B are any two non-empty sets and each element of set A is related with one and only one element of set B by some rule, relation or correspondence, then it is called a function from set A to B and. is denoted by f: A → B.
Question 2.
Define domain and co-domain of a function.
Answer:
Domain of a function: Suppose, f: A → B, the set A is called domain of the function J. It is denoted by Df.
Co-domain of a function : Suppose, f: A → B, the set B is called the co-domain of the function f.
Question 3.
Define range of a function.
Answer:
Suppose f: A → B. then a set of images or functional values of all the elements of set A is called range of function f It is denoted by f/.
Rf = {f(x) | x ∈ A).
The range of a function may be co-domain itself or a subset of co-domain.
![]()
Question 4.
g: A → N, A = {x| x ∈ N, 1 < x ≤ 4}; g(x) = x + 1. Find range of function g.
Answer:
A = {x | x ∈ N, 1 < x ≤ 4}
A = {2, 3, 4} ⇒ Domain g [x] = x + 1
∴ g (2) = 2 + 1 = 3, g (3) = 3 + 1 = 4, g (4) = 4 + 1 = 5
Range of function Rf = {g (x) | x ∈ A}
= {g (2), g (3), g (4)} = {3, 4, 5}
Question 5.
k:X → Y, X = {t| t ∈ Z, -3 < t ≤ 3};
Y = {a| a ∈ N, 1 ≤ a≤ 20}; k(t) = t2+2.
State the type of function k.
Answer:
k:X → Y
Domain X={t| t ∈ Z, -3 ≤ t ≤ 3)
= {-3, -2, -1, 0, 1, 2, 3}
k (t) = t2 + 2
∴ k(- 3) = (-3)2 + 2 = 9 + 2 = 11,
k (3) = (3)2 + 2=11,
k (- 2) = (- 2)2 + 2 = 4 + 2 = 6,
k (2) = (2)2 + 2 = 6,
k(- 1) = (- 1)2 + 2 = 1 + 2 = 3,
k (1) = (1)2 + 2 = 3,
k (0) = 0 + 2 = 2
Co-domain Y = {a|a ∈ N ⇒ 1, a ≤ 20}
= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …, 18, 19, 20}
Here, for two different elements (-3, 3) of domain, their images in co-domain are k (- 3) = k (3) = 11. Therefore, function k is many one function.
Question 6.
h : A → B, A = {1, 2, 3},
B = {3, 4, 5, 6, 7, 8}, h (x) = x + 5. State the type of function h.
Answer:
h : A → B
A = {1, 2, 3} and h (x) = x + 5
∴ h (1) = 1 + 5 = 6, h (2) = 2 + 5 = 7, h (3) = 3 + 5 = 8
B = {3, 4, 5, 6, 7, 8}
For the elements 1, 2, 3 of domain
h (1) ≠ h (2) ≠ h (3).
Therefore, function ft is one-one function.
Question 7.
If P : A → B, P(x) = 2x – 3 and Rf = {-2, -1, 0}, then find domain of the function.
Answer:
P (x) = 2x – 3
Rf = {-2, – 1, 0}
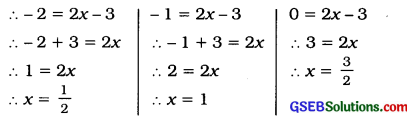
Therefore, domain of the function = {\(\frac{1}{2}\), 1, \(\frac{3}{2}\)}
Question 8.
If f(x) = 1 – \(\frac{1}{1-x^{2}}\) x ∈ R – {-1, 1), then find f(2) – f(-2).
Answer:

![]()
Question 9.
If domain of f(x) = \(\frac{x-3}{x+4}\) is (0, 3, 6) then find its range.
Answer:
f(x) = \(\frac{x-3}{x+4}\), Domain = {0, 3, 6}
f(0) = \(\frac{0-3}{0+4}=-\frac{3}{4}\)
f(3) = \(\frac{3-3}{3+4}=\frac{0}{7}\) = 0
f(6) = \(\frac{6-3}{6+4}=\frac{3}{10}\)
Range Rf = {f(x) | x ∈ Domain}
= {f(0), f(3), f(6)}
∴ Rf = {-\(\frac{3}{4}\), 0, \(\frac{3}{10}\)}
Question 10.
If f(x) = \(\frac{x^{2}(x+1)^{2}}{4}\) is a real function then find the value of f(3) -f(2).
Answer:

Question 11.
If f:R → R and f(x) = x2 + 2x – 1, then state the type of function f.
Answer:
f: R → R
f(x) = x2 + 2x – 1
Domain={… -2, -1. 0. 1, …}
Co-domain={… -1, -2, -1, 2,…}
Here, for two different elements -2 and 0 of domain, their Images are same In co-domain.
Therefore function f is many-one function.
Question 12.
If f(x) = \(\frac{2 x-4}{x+7}\) is a real function then for which value of x the image is zero?
Answer:
f(x) = \(\frac{2 x-4}{x+7}\)
Image = 0. Therefore, put f(x) = 0
0 = \(\frac{2 x-4}{x+7}\)
∴ 0 = 2x – 4 ∴ 4 = 2x
Therefore, x = 2, the Image is zero.
Question 13.
f:Z – {2} → Z, f(x) = \(\frac{x^{2}+x-6}{x-2}\) State the type of the function.
Answer:
f:Z – {2} → Z
∴ Domain = {……., -3, -2, 0, 1, 3, 4,….}

Here, for two different elements of domain, their Images are not same. Therefore, the given function is one-one function.
Question 14.
For a real function, f(x) = 6x3 – 5x + 15, find the value of f (O).
Answer:
f(x) = 6x3 – 5x + 15
∴f(0) = 6 × 0 – 50 + 15
= 0 – 1 + 15 = 14
∴f(0)=14
Question 15.
If f(x) = x3 – 2x + \(\frac{1}{x}\) is a real function then find the value of f(3) + f(-3).
Answer:

Section – D
Answer the following questions as required:
Question 1.
For f:A → B, A = {10, 20, 30); B = (18, 48, 98, 128, 148); f(x) = 5x – 2; obtain domain, co-domain and range.
Answer:
f: A → B, A = {10, 20, 30}
B = {18, 48. 98. 128. 148}
f(x) = 5x – 2
Domain: A = (10, 20, 30)
Co-domaln: B = {18, 48, 98, 128, 148}
Range:Rf ={f(x) | x ∈ A}
= {f(10), f(20), f(30)}
Now,f(10) = (5 × 10) – 2 = 50—2 = 48
f(20) = (5 × 20) – 2 = 100 – 2=98
f(30) = (5 × 30) – 2 = (150 – 2) = 148
∴ Range Rf = (48, 98, 148)
![]()
Question 2.
Obtain demain, co-domain and range for
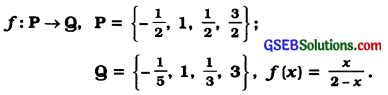
Answer:

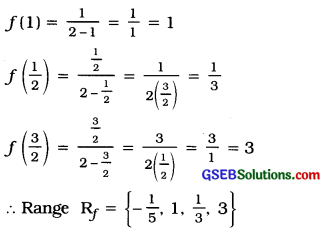
Question 3.
If f:R – {0} → R, f(x) = \(\frac{1}{x}\left(1+\frac{1}{x}\right)\) – 1 then find the value of f(-1), f(-2) and f(\(\frac{1}{2}\))
Answer:

Question 4.
For the function f:A → B, f(x) = 4x – 3;
Rf = (9, 13, 17, 25}, then find Df.
Answer:
f:A → B, f(x) = 4x – 3, Rf = {9 13, 17, 25}
f(x) = 9 ∴9 = 4x – 3 ∴ 12 = 4x ∴x = 3
f(x) = 13 ∴13 = 4x-3 ∴16 = 4x ∴x = 4
f(x) = 17 ∴17 = 4x – 3 ∴ 20 = 4x ∴x = 5
f(x) = 25 ∴25 = 4x – 3 ∴ 28 = 4x ∴ x = 7
Hence, Df = {3, 4, 5, 7),
Question 5.
For the real function f (x) = 2x2 – 5x + 4, find the value of x, for which f (3x) – 3f(x) + 5 = 0.
Answer:
f(x) = 2x2 – 5x + 4 Now, f(3x) – 3f(x) + 5 = 0
∴ 2 (3x)2 – 5 (3x) + 4 – {3 (2x2 – 5x + 4)} + 5 = 0
∴ 2 (9x2) – 15x + 4- 6x2 + 15x- 12 + 5 = 0
∴ 18x2 – 6x2 – 15x + 15x + 4 – 12 + 5 = 0
∴ 12x2 – 3 = 0
∴ 12x2 = 3
∴ x2 = \(\frac{3}{12}=\frac{1}{4}=\left(\pm \frac{1}{2}\right)^{2}\)
∴ x = ± \(\frac{1}{2}\)
Hence, when x = ± \(\frac{1}{2}\) then f(3x) – 3f(x) + 5 = 0.
Question 6.
If f: A → M, A = {x | x ∈ N, 1 ≤ x < 5} and M = {x | x ∈ N, 1 ≤ x ≤ 20} and f(x) = x2 + 1, then find the range of f.
Answer:
f: A → M
A = {x | x ∈ N, 1 ≤ x < 5}
= {1, 2, 3, 4}
M = {x | x G N, 1 ≤ x ≤ 20}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
f(x) = x2 + 1
Range of f Rf= {f(x) | x ∈ A}
= {f(1), f(2), f(3), f(4)}
Now, f(x) = x2 + 1
∴ f(1) = (1)2 + 1 = 1 + 1 = 2
f(2) = (2)2 + 1 = 4+ 1 = 5
f(3) = (3)2 + 1 = 9 + 1 = 10
f(4) = (4)2 + 1 = 16 + 1 = 17
Hence, Range of f Rf = {2, 5, 10, 17}
Question 7.
If f(x) = \(\frac{x^{2}-4}{x-2}\) where x ∈ Z – {2} then find the value of f(0) + f(1) – f(-2).
Answer:
f(x) = \(\frac{x^{2}-4}{x-2}=\frac{(x+2)(x-2)}{x-2}\) = x + 2
∴ f(0) + f(1) – f(-2)
= (0 + 2 + (1 + 2) – (-2 + 2)
= 2 + 3 – 0
= 5
![]()
Question 8.
If the domain of a function f: A → N ∪ {0}; f(x) = \(\sqrt{x^{2}-16}\) is A = {4, 5}, then find its range.
Answer:
f(x) = \(\sqrt{x^{2}-16}\); Domain = {4, 5}
Range Rf = {f(x) | x ∈ Domain}
= {f(4), f(5)}
Now, f(x) = \(\sqrt{x^{2}-16}\)
∴ f( 4) = \(\sqrt{(4)^{2}-16}\)
= \(\sqrt{16-16}\) = 0
f(5) = \(\sqrt{(5)^{2}-16}\)
= \(\sqrt{25-16}=\sqrt{9}\) = 3 (∵ x is positive.}
Hence, Range Rf = {0, 3}
Question 9.
If f (x) = x2 and g(x) = 5x – 6, where x ∈ {2, 3, 4}, check the equality of the functions.
Answer:
f(x) = x2, g (x) = 5x – 6, Domain = (2, 3, 4} For fix) =x2, Range Ry= {f(2), f(3), f{4}}
= (4, 9, 16}
For g (x) = 5x – 6,
Range Rf = {g (2), g (3), g (4)}
∴ g(2) = 5 (2) – 6 = 10 – 6 = 4 ,
g (3) = 5(3) – 6 = 15 – 6 = 9
g (4) = 5 (4) – 6 = 20 – 6 = 14
Rf = {4, 9, 14}
Domains of the functions fix) and g (x) are same but their range are not same. Hence, the given functions are unequal functions.
Question 10.
If k : R → R, k(x) = x2 + 3x – 12; then ‘ determine the type of the function k.
Answer:
k : R → R
∴ Domain = {…, -3, -2, -1, 0, 1, 2, …}
k (x) = x2 + 3x – 12
∴ k (- 3) = (- 3)2 + 3 (- 3) – 12 = – 12
k (- 2) = (- 2)2 + 3 (- 2) – 12 = 4 – 6 – 12 = – 14
k (- 1) = (- 1 )2 + 3 (- 1) – 12 = 1 – 3 – 12 = -14
k(0) = 0 + 0 – 12 = – 12
k(1) = 1 + 3 – 12 = -8
k (2) = 4 + 12 – 12 = 4
∴ Co-domain = {…, -12, -14, -14, -12, -8, 4, …}
Here, for the elements – 3 and 0, – 2 and – 1 of domain, their images are same. Therefore function k is many-one function.
Question 11.
If f(x) = x (3x – 2), g (x) = x3 and x ∈ {0, 1, 2}; then prove that f and g are equal functions.
Answer:
f(x) = x (3x – 2), x ∈ {0, 1, 2} ……………(1)
∴ Range Rf = {f(0), f(1), f(2)}
Now, f(0) = 0(3 × 0 – 2) = 0,
f(1) = 1 (3 × 1 – 2) = 1,
f(2) = 2 (3 × 2 – 2) = 2 (6-2) = 2×4 = 8
Range Rf = {0, 1, 8} …………….(2)
g (x) = x3, x ∈ {0, 1, 2} ………………..(3)
∴Range Rf ={g(0), g(1), g(2)}
Now, g (0) = 0, g(1) = 1. g(2) = 8
∴ Range Rf = {0,, 1, 8} …………….(4)
From (1) and (3) the domain off and g is equal.
From (2) and (4) the range of / and g is equal.
Hence, f and g are equal functions.
Question 12.
If f(x) = \(\frac{2 x+3}{5 x+2}\) x ∈ R – {-\(\frac{2}{5}\)}; then find the value of f(2).f(1).
Answer:
f(x) = \(\frac{2 x+3}{5 x+2}\)

Question 13.
If f (x) = 2x2 + \(\frac{1}{x}\), x ∈ R; obtain the value of f(3) + f(-3).
Answer:
f(x) = 2x2 + \(\frac{1}{x}\)
∴ f(3) + f( – 3) = 2 (3)2 +\(\frac{1}{3}\) + 2 (- 3)2 + \(\frac{1}{(-3)}\)
= (2 × 9) + \(\frac{1}{3}\) + (2 × 9) – \(\frac{1}{3}\) = 18 + 18 = 36
![]()
Question 14.
If f(x) = 15x3 – 4x2 + x + 10, x ∈ R; obtain the value of \(\frac{f(2)}{f(1)}\)
Answer:
f(x) = 15x3 – 4x2 + x + 10
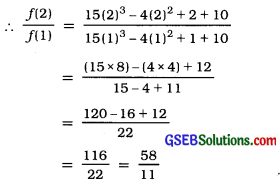
Question 15.
If f:A → N, A = {500, 1000, 1300, 1400}, f(x) = \(\sqrt{5600-4 x}\), XER then find the value of f(x) for x = 1000. Also, for which value of x, f(x) = 20?
Answer:
f(x)= \(\sqrt{5600-4 x}\)
Putting x = 1000,
f(4)= \(\sqrt{5600-4(1000)}\)
= \(\sqrt{5600-4000}\)
= \(\sqrt{1600}\) =40
f(x) = 20
∴ 20 = \(\sqrt{5600-4 x}\)
∴ 400 = 5600 – 4x
4x = 5200
(20)2 = 5600 – 4x
∴ 4x = 5600 – 400
∴ x = 1300
Hence, when x = 1300. then f(x) = 20.