GSEB Solutions Class 11 Statistics Chapter 9 Geometric Progression Ex 9

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 9 Geometric Progression Ex 9 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 9 Geometric Progression Ex 9

Section – A

Choose the correct option from those given below each question :

Question 1.
Find the 6th term of a G.P. 0.2, 1, 5, …
(a) 25
(b) 0.5
(c) 0.1
(d) 625
Answer:
(d) 625

Question 2.
If the first term of a G.P. is ‘a and the common ratio is ‘b’. Find the (n + 1)th term,
(a) abⁿ
(b) arⁿ
(c)ab^n-1
(d) ar^n-1
Answer:
(a) abⁿ

Question 3.
For a G.P. 1, √3, 3, 3√3 find the 5th term?
(a) 9
(b) 9√3
(c) 27
(d) \(\frac{(\sqrt{3})^{5}-1}{(\sqrt{3}-1)}\)
Answer:
(a) 9

Question 4.
For a G.P., T₁ = a and T₅ = \(\frac{1}{a}\): where, a > 0 then obtain Its third term.
(a) a²
(b) 1
(c) \(\frac{(\sqrt{3})^{5}-1}{(\sqrt{3}-1)}\)
(d) a
Answer:
(b) 1

Question 5.
For a G.P. \(\frac{1}{9}, \frac{1}{3}\) 1 …, find the seventh term.
(a) 6561
(b) 243
(c) 81
(d) \(\frac{1}{81}\)
Answer:
(c) 81

Question 6.
Find the common ratio of a G.P. whose nth term is 3(2^n-1).
(a) 3
(b) 2
(c) 6
(d) 1
Answer:
(b) 2

Question 7.
For a G.P. 0.4, 0.04, 0.004, ….find the common ratio.
(a) 10
(b) 0.4
(c) 4
(d) 0.1
Answer:
(d) 0.1

Question 8.
If x, 10, -25 are in G.P, then find the value of x.
(a) 4
(b) – 25
(c) – 4
(d) 2
Answer:
(c) – 4

Question 9.
The common ratio of a G.P. is -1 and its first term is -1, then find the sum of the first six terms of the G.P.
(a) 0
(b) – 1
(c) 1
(d) 6
Answer:
(a) 0

Question 10.
The common ratio of a G.P. is 1 and S₁₀ = 40, then find the first term.
(a) 0
(b) 10
(c) 4
(d) 400
Answer:
(c) 4

Section – B

Answer the following questions in one sentence:

Question 1.
What is the nth term of the G.P. ar, ar², ar³ …?
Answer:
The nth term of the G.P. ar, ar², ar³, … is a.rⁿ.

Question 2.
Find the common ratio of the G.P. 0. 1, 0.01, 0.001
Answer:
The common ratio of the G.P. 0.1, 0.01, 0.001 is r = \(\frac{0.01}{0.1}\) = 0.1.

Question 3.
Find the sum of twenty terms of the G.P. 7, 7, 7,….
Answer:
G.P. 7, 7, 7, …
Here, a = 7; r = 1; n = 20. S_n = na
S₂₀ = 20 × 7 = 140

Question 4.
If in a G.P. the nth term is given as T_n = 2^{n + 1}, find the common ratio.
Answer:
T_n = 2^{n + 1}. For G.P. T_n = a.r^{n – 1}. Comparing these two common ratio = 2.

Question 5.
The numbers 4, 1, y are in G.P. Find the value of y.
Answer:
Numbers 4, 1, y are in G.P.
∴\(\frac{1}{4}=\frac{y}{1}\)
∴ 4y = 1
∴ y = \(\frac{1}{4}\)

Question 6.
For a G.P., sum of any two consecutive terms is zero, then what will be the common ratio?
Answer:
Sum of two consecutive terms = 0
∴ T₁ + T₂ = 0
∴ a + ar = 0
∴ a (1 + r) = 0
∴ 1 + r = 0
∴ r = – 1
Hence, common ratio will be r = -1.

Question 7.
For a G.P., if S₇ = 15 and S₆ = 11, then find the seventh term of the G.P.
Answer:
S₆ = 15, S₅ = 11
Now, T_n+1 = S_n+1 – S_n. We have to find 6th term. Therefore, put n = 5.
∴ T₆ = S₆ – S₅ = 15 – 11 = 4

Question 8.
State whether the statement “if a, b, c, d are in G.P., then ad = be” is true or false.
Answer:
a, b, c, d are in G.P.
∴ \(\frac{b}{a}=\frac{c}{b}=\frac{d}{c}\)
∴ \(\frac{b}{a}=\frac{d}{c}\)
∴ ad = be is true.

Question 9.
State whether the statement “T₁ = S₁’ is true or false in G.P.
Answer:
For G.P. T₁ = First term, S₁ = Sum of first term = T₁. Hence, the statement “T₁ = S₁ is true.

Section – C

Answer the following questions as required:

Question 1.
Define Geometric progression.
Answer:
If a and r non-zero real numbers, the sequence whose nth term is T_n; = a . r^n-1 for an integer n ≥ 1, is called the geometric progression. Where, a = first term of sequence and r = common ratio of sequence.

Question 2.
Define Geometric series.
Answer:
If the consecutive terms of a geometric progression are expressed in terms of a and r as a. ar, ar²,…, then a + ar + ar² +…+a.r^n-1 is called geometric series. It is denoted by S. I.e.,
S = a + ar + ar² +…+a.r^n-1

Question 3.
If in a G.P., common ratio is 1 and S₈ = 24, find the first term of the G.P.
Answer:
If in a G.P. common ratio r = 1, then S_n = n . a
S₈ = 8a
∴ 24 = 8a
∴ a = 3
Hence, the first term of the G.P. is 3.

Question 4.
For a G.P., T₁ = 2 and the product of the first three terms is 1000. Find the common ratio.
Answer:
For a G.P., T₁ = 2
∴ a = 2
Now, T₁; × T₂ × T₃ = a × ar × ar²
∴ 1000 = 2 × 2r × 2r³
∴ 1000 = 8r³;
∴ r³ = = 125 = (5)³
(∴ Index are equal then base are equal)
Hence, common ratio r = 5

Question 5.
For a G.P., a = 2 and r = 3; then find the sum of first four terms.
Answer:
a = 2, r = 3, n = 4
Sn = \(\frac{a\left[r^{n}-1\right]}{r-1}\)
Putting n = 4; a 2; r = 3 in the formula,
Sn = \(\frac{2\left[(3)^{4}-1\right]}{3-1}=\frac{2[81-1]}{2}\) = 80
Hence, the sum of first four terms of a G.P. Is 80.

Question 7.
For a G.P., a = \(\frac{4}{9}\) and r = \(\frac{-3}{2}\). Find T₃.
Answer:
a = \(\frac{4}{9}\), r = T₃ =?
T = \(\left(\frac{4}{9}\right)\left(-\frac{3}{2}\right)^{3-1}\)
= \(\left(\frac{4}{9}\right)\left(-\frac{3}{2}\right)^{2}\)
= \(\frac{4}{9} \times \frac{9}{4}\)
= 1
Hence, the third term of a G.P. is 1.

Question 8.
If the common ratio of a geometric progression is 2, find the ratio of Its 7th and 3rd terms.
Answer:

Question 9.
Find the required term of the following sequence using sequence formula:
(i) 2, 10, 50, … (6th term)
Answer:
2, 10, 50, … T₆ = ?
Here. a = 2, r = \(\frac{10}{2}\) = 5, n = 6
T₆ = a.r^n-1
∴ T₆ = 2.(5)^6-1
= 2 (5)⁵
= 2 × 3125
= 6250

(ii) 100, 50, 25, … (7th term)
Answer:
Here, a = 100; r = \(\frac{50}{100}=\frac{1}{2}\) = n = 7
T_n = a.r^n-1
∴T₇ = 100\(\left(\frac{1}{2}\right)^{7-1}\)
= 100\(\left(\frac{1}{2}\right)^{6}\)]
= \(\frac{100}{64}=\frac{25}{16}\)

(iii) \(\frac{1}{3}, \frac{2}{9}, \frac{4}{27}\)…….. (8th term)
Answer:

(iv) 2, 2√2, 4, … (5th term)
Answer:
Here. a = 2; r = \(\frac{2 \sqrt{2}}{2}\) = √2; n = 5
T_n = a.r^n-1
∴ T₅ = 2\((\sqrt{2})^{5-1}\) = 2\((\sqrt{2})^{4}\) = \(\left(2^{\frac{1}{2}}\right)^{4}\) = 2(2)² = 2 × 4 = 8

Section – D

Answer the following questions as required:

Question 1.
For a given G.P., if T₅ = 405 and T₇ = 3645; then find T₄.
Answer:
T₅ = 405, T₇ = 3645, T₄ =?
T_n = a.r^n-1
∴ T₅ = a. r⁴
∴ 405 = a. r⁴ ……….(1)

T₇ = a. r⁶
∴ 3645 = a. r⁶ ………(2)

T₄ = a. r³ …….(3)

Taking the ratio of results (2) and (1),
\(\frac{3645}{405}=\frac{a r^{6}}{a r^{4}}\)
∴ 9 = r²
∴ r = ± 3

Putting r = ± 3 In result (1),
405 = a (± 3)⁴
∴ 405 = a × 81
∴ a = \(\frac{405}{81}\) = 5
Putting a = 5 and r = ±3 In result (3).
T₄ = 5(±3)³
∴ T₄ = 5 (± 27)
∴ T₄ =± 135

Question 2.
Find T5 and S4 of the geometric progression If the first term is and common ratio is \(\frac{2}{3}\)
Answer:
Here. a = \(\frac{27}{16}\); r = \(\frac{2}{3}\); T₅ =?; S₄ =?
T_n = a r^n-1

Question 3.
For a given G.P., a = 4 and T₅ = \(\frac{1}{4}\); then find T₇.
Answer:
Here, a = 4: T₅ = \(\frac{1}{4}\); T₇ =?

Question 4.
For a given G.P., if T₂ = 9 and T₅ = 243; then find S₄.
Answer:
Here. T₂ = 9; T₅ = 243; S₄ =?
T = a. r^n-1
∴ T₂ = a r^2-1
∴ 9 = ar ………..(1)
T₅ = a r^5-1
∴ 243 = ar⁴ …………..(2)

Taking ratio of results (2) and (1)
\(\frac{243}{9}=\frac{a r^{4}}{a r}\)
∴ 27 = r³
∴ (3)³ = r3
∴ r = 3

Putting r = 3 In the result (1),
9 = 3a ∴ a = 3
Now, S_n = \(\) (∴ r > 1)
∴ S₄ = \(\frac{a\left[r^{n}-1\right]}{r-1}\)
= \(\frac{3\left[(3)^{4}-1\right]}{3-1}\)
= \(\frac{3[81-1]}{2}\)
= \(\frac{3 \times 80}{2}\) = 120

Question 5.
The first term of a G.P., Is 10 and T₄ = 0.08. Find sum of first three terms.
Answer:
Here, a = 10, T₄ = 0.08, S₃ =?

Question 6.
For a geometric progression, T₁² = T₂² and T₃ = 64. Write the sequence.
Answer:
Here, T₁² = T₂²; T₃ = 64
T_n = a.r^n-1

a = r :a = 4
First term = 4 and common ratio r = 4
Hence, the sequence obtained Is 4, 16. 64, …

Question 7.
If 5, m, 20, t are In geometric progression; find m and t.
Answer:
5, m, 20, t are In G.P.
∴ \(\frac{m}{5}=\frac{20}{m}\) and \(\frac{t}{20}=\frac{20}{m}\)
∴ m² = 100
∴ m = ±10
∴ 400 = mt
Putting m = ±10
400 = ±10(t)
∴ t = \(\frac{400}{\pm 10}\) = ±40

Question 8.
For a given G.P., If a = 10, r = 0.1 and T_n = 0.01; then find n.
Answer:
a = 10, r = 0.1, T = 0.01, n =?
T_n = a.r^n-1
∴ 0.01 = 10(0.1)^n-1
∴ \(\frac{0.01}{10}\) = (0.1)^n-1
∴ 0.00 1= (0.1)^n-1
∴ (0.1)³ = (0.1)^n-1
∴ 3 = n – 1
∴ n = 4

Question 9.
For a given G.P., If a = 1, r = 3 and S_n = 121; then find n.
Answer:
a = 1, r = 3, S = 121, n =?

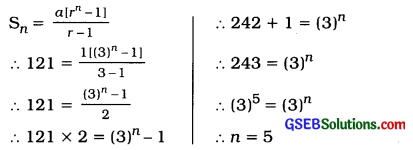
Question 10.
If S_n = \(\frac{2}{3}\)(2ⁿ-1), find T₄.
Answer:
S_n = \(\frac{2}{3}\)(2ⁿ-1)

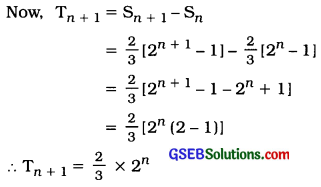
we have to find 4th term. Therefore, put n = 3
T₄ = \(\frac{2}{3}\) × 2³
= \(\frac{2}{3}\) × 8 = \(\frac{16}{3}\)

Question 11.
If S_n = 4(3ⁿ – 1), find T_n+1.
Answer:
S_n = 4 (3ⁿ – 1)
Now, T_n+1 = S_n+1 – S_n
= 4[3ⁿ⁺¹ – 1] – 4[3ⁿ – 1]
= 4[3ⁿ⁺¹ – 1 – 3ⁿ + 1]
= 4[3ⁿ(3 – 1)]
= 4(3ⁿ × 2)
∴ T_n+1 = 8(3)ⁿ

Question 12.
Find the product of the first three terms of a G.P. whose second term is 5.
Answer:
T₂ = 5 ∴ 5 = ar
The product of the first three terms of a G.P.
= T₁ × T₂ × T₃
= a × ar × ar₃
= a₃ r₃ = (ar)₃
Putting ar = 5,
The product of the first three terms of a G.P. = (5)₃ = 125.

Question 13.
How many terms of a geometric progression 2, 4, 8, 16, … would add to 126?
Answer:
Here. GP. is 2; 4, 8, 16,…
∴ a = 2, r = \(\frac{4}{2}\) =2, S_n = 126. n =?
Now, S_n = r-1 (,r > 1)
∴ 126 = \(\frac{2\left[2^{n}-1\right]}{2-1}\)
∴ \(\frac{126}{2}\) = 2ⁿ – 1
∴ 63 + 1 = 2ⁿ
∴ (2)⁶ = 2ⁿ
∴ n = 6

Question 14.
If for a G.P., T_n = 324, S_n = 484 and r = 3; find a and n.
Answer:
T_n = 324, S_n = 484, r = 3, a =?, n =?
Now, S_n = \(\frac{r T_{n}-a}{r-1}\)
∴ 484 = \(\frac{3(324)-a}{3-1}\)
∴ 484 = \(\frac{972-a}{2}\)
∴ 484 × 2 = 972 – a
∴ a = 972 – 968
a = 4
Now, T_n = a.r^n-1
∴ 324 = 4(3)^n-1
∴ \(\frac{324}{4}\) = (3)^n-1
∴ (3)⁴ = (3)^n-1
∴ 4 = n – 1 ( Base are equal, Index are also equal)
∴ n = 5

Question 15.
Find the sum of required terms for the following sequence using series formula:
(1) 4, 16, 64, … (first 4 terms)
Answer:

(2) 2, 3, \(\frac{9}{2}\), … (first 5 terms)
Answer:

(3) 100, 20, 4, … (first 5 terms)
Answer:

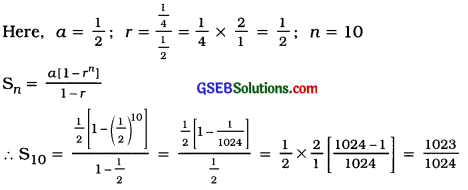
(4) \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}\) … (first 10 terms)
Answer:

Section – E

Answer the following questions as required:

Question 1.
If the three positive numbers k + 4, 4k-2 and 7k + 1 are in G.P., find k.
Answer:
k + 4, 4k-2, 7k + 1 are in G.P.
\(\frac{4 k-2}{k+4}=\frac{7 k+1}{4 k-2}\)
∴ (4k-2) (4k- 2) = (7k + 1) (k + 4)
∴ 16k² – 16k + 4 = 7k² + 28k + k + 4
∴ 16k² – 7k² – 16k – 28k – k + 4 – 4 = 0
∴ 9k² – 45k = 0
∴ 9k (k – 5) = 0
∴ 9k = 0
OR
k – 5 = 0
∴ k = 0 OR k = 5
Numbers are positive. Hence, k = 5

Question 2.
Find the maximum value of n such that the sum of the first n terms of a G.P. 1, 3, 32, 3 … does not exceed 365.
Answer:
Here, a = 1; r = \(\frac{3}{1}\) = 3; The sum of the first n terms does not exceed 365, i.e., S_n ≤ 365.
Now, S_n = r-i
Putting a = 1; r = 3.
S_n = \(\frac{1\left[3^{n}-1\right]}{3-1}\)
S_n = \(\frac{3^{n}-1}{2}\)

Now, S_n ≤ 365
∴ \(\frac{3^{n}-1}{2}\) ≤ 365
∴3ⁿ – 1≤ 365 × 2
∴ 3ⁿ ≤ 730 + 1
∴ 3ⁿ ≤ 731

We now tabulate values of 3’ for different positive values of n as shown in the following table and we shall take the maximum value of n for which 3ⁿ ≤ 731.

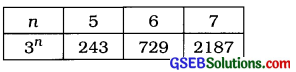
For n = 7, 3ⁿ = 2187 which is more than 731.
∴ n = 6 is the maximum value of n, for which 3ⁿ ≤ 731.

Question 3.
Find the minimum value of n such that the sum of the first n terms of a G.P. 1, 2, 22, 2, … is greater than or equal to 2000.
Answer:
Here, a = 1; r = \(\frac{2}{1}\) = 2, The sum of first ii terms is greater than or equal to 2000, i.e..
S_n ≥ 2000.
Now, S_n = \(\frac{a\left[r^{n}-1\right]}{r-1}\)
Putting a = 1; r = 2,
S_n = \(\frac{1\left[2^{n}-1\right]}{2-1}\)= 2ⁿ – 1
S_n ≥ 2000
∴ 2ⁿ – 1 ≥ 2000
∴ 2ⁿ ≥ 2000 + 1
∴ 2ⁿ ≥ 2001
We now tabulate values of 2ⁿ for different positive values of n as shown in the following table and we shall take the minimum value
of n for which 2ⁿ ≥ 2001.

From the table we can see that for n = 11, 2ⁿ = 2048 which is greater than 2001.
∴ For n = 11, 2n 2001.
Hence, n = 11 is minimum value of n.

Question 4.
The sum of the first five terms of the G.P. y, \(\frac{y}{2}\), \(\frac{y}{9}\)…. (where, y > 0) is 121. Find y.
Answer:
Here, a = y; r = \(\frac{\frac{y}{3}}{y}=\frac{1}{3}\); S₅ = 121
S_n= \(\frac{a\left[1-r^{n}\right]}{1-r}\) (∵ r < 1)
Putting n = 5; a = y; r = \(\frac{1}{3}\),

Question 5.
For a geometric progression, S₄ = 10 S₂. Find the common ratio.
Answer:
S₄ = 10 S₂
S_n = \(\frac{a\left[r^{n}-1\right]}{r-1}\)
S₄ = \(\frac{a\left[r^{4}-1\right]}{r-1}\) and S₂ = \(\frac{a\left[r^{2}-1\right]}{r-1}\)

Now, S₄ = 10 S₂
\(\frac{a\left[r^{4}-1\right]}{r-1}\) = 10 × \(\frac{a\left[r^{2}-1\right]}{r-1}\)
∴ r⁴ – 1 = 10 (r²– 1)
∴ (r² – 1) (r² + 1) = 10 (r² – 1)
∴ r² + 1 = 10
∴ r² = 10- 1
∴ r² = 9
∴ r = ±3

Question 6.
For a geometric progression, the ratio of sum of the fifth and the third term to the difference of the fifth and the third term is 5:3. Find r.
Answer:
Here, (T₅ + T₃):(T₅ – T₃) = 5 : 3
Now, T_n = ar^n-1
∴ T₅ = ar⁴ and T₃ = ar²
(T₅ + T₃) : (T₅ – T₃) = 5 :3
∴ \(\frac{a r^{4}+a r^{2}}{a r^{4}-a r^{2}}=\frac{5}{3}\)
∴ \(\frac{a r^{2}\left(r^{2}+1\right)}{a r^{2}\left(r^{2}-1\right)}=\frac{5}{3}\)
∴ \(\frac{r^{2}+1}{r^{2}-1}=\frac{5}{3}\)
∴ 3r² + 3 = 5r² – 5
∴ 3 + 5 = 5r² – 3r²
∴ 8 = 2r²
∴ r² = \(\frac{8}{2}\) = 4
∴ r = ± 2

Question 7.
The sum and the product of the three concecutive numbers in a geometric progression are 31 and 125 respectively. Find the three numbers of the G.P.
Answer:
Suppose, the three consecutive numbers In a GP. are \(\frac{a}{r}\), a, ar.
The sum of the three consecutive terms = 28
∴ \(\frac{a}{r}\) + a + ar = 28
∴ \(\frac{a+a r+a r^{2}}{r}\) = 28
∴ a + ar + ar² = 28r ………..(1)

The product of the three consecutive temrs = 512
∴ \(\frac{a}{r}\) × a × ar = 512
∴ a³ = 512 = (8)³
∴ a = 8
Putting a = 8 In the result 1,
8 + 8r + 8r² = 28r
∴ 8r2+8r-28r+80
∴ 8r² – 20r + 8 = 0
∴ 2r² – 5r + 2 = 0
∴ 2r² – 4r – r + 2 = 0
∴ 2r(r – 2) – 1(r – 2)=O
∴ (r – 2)(2r – 1) = 0
∴ r – 2 = 0 OR 2r – 1 = 0
∴ r = 2 OR r = \(\frac{1}{2}\)
Putting a = 8 and r = 2 in \(\frac{a}{r}\), a, ar,
Three consecutive numbers, we get
\(\frac{8}{2}\), 8, 8 × 2 ⇒ 4, 8, 16

Putting a = 8 and r = \(\frac{1}{2}\) In \(\frac{a}{r}\), a, ar,
Three consecutive numbers we get are :
\(\frac{8}{\frac{1}{2}}\), 8, 8 × \(\frac{1}{2}\) ⇒ 16, 8, 4.

Hence, three consecutive numbers are
4, 8, 16 OR 16, 8, 4.

Question 8.
The sum and the product of the three consecutive terms of G.P. are 6 and -64 respectively. Find the three terms of the G.P.
Answer:
Suppose, three consecutive terms of G.P. are
\(\frac{a}{r}\), a, ar. r
The sum of the three consecutive terms = 6
∴ \(\frac{a}{r}\) + a + ar = 6 .
\(\frac{a+a r+a r^{2}}{r}\) = 6
a + ar + ar² = 6r ………….(1)

The product of the three consecutive terms = -64
∴ \(\frac{a}{r}\) × a × ar = – 64
a³ = – 64 = (- 4)³
∴ a = – 4
Putting a = -4 in the result (1),
– 4 – 4r – 4r² = 6r
4r² + 4r + 6r + 4 = 0
4r² + 10r + 4 = 0
∴ 2r² + 5r + 2 = 0
∴ 2r² + 4r + r + 2 = 0
∴ 2r(r + 2) + 1 (r + 2) = 0
(r + 2) (2r + 1) = 0
r + 2 = 0 OR 2r + 1 = 0
∴ r = – 2 OR r = –\(\frac{1}{2}\)
Putting a = – 4 and r = – 2 in \(\frac{a}{r}\); a; \(\frac{a}{r}\),
Three consecutive terms:
\(\frac{-4}{-2}\), -4, (-4) (- 2} ⇒ 2, -4, 8.

Putting a = – 4 and r = \(\frac{1}{2}\) in y; a; y
Three consecutive terms :
\(\frac{-4}{-2}\), -4, (-4)\(\left(-\frac{1}{2}\right)\) ⇒ 8, -4, 2.
Hence, three consecutive terms are 2, -4, 8 OR 8, -4, 2.

Question 9.
A construction company offers a scheme on a flat to attract customers. In this scheme, customer has to pay ₹ 10,000 as the first installment and has to pay double the amount of the preceeding installment in the subsequent annual installments. What is the total amount that the customer has to pay upto 10 installments?
Answer:
Here, the first installment a = ₹ 10,000 Yearly installment is double the amount of the preceeding installment, r = 2
10 installments are to be paid.
∴ n = 10
The total amount that the customer has to pay up to 10 installments = S_n
Putting n = 10; a = 10,000; r = 2,
S₁₀ = \(\frac{10,000\left[(2)^{10}-1\right]}{2-1}\)
= 10,000 (1024- 1)
= 10,000 × 1023
= ₹ 1,02,30,000
Hence, the customer has to pay ₹ 1,02,30,000

Question 10.
A banker counts 128 notes in the first minute and there after he counts half the number of flotes he counted In the previous minute. How many notes he would count In five minutes?
Answer:
In the first minute a banker counts 128 notes.
∴ a = 128
There after, in every minute he counts half the number of flotes he counted In the previous minute.
∴ r = \(\frac{1}{2}\)

Total number of notes counted in five minutes = S₅
Now, S_n = \(\frac{a\left[1-r^{n}\right]}{1-r}\)
Putting n = 5; a = 128; r = \(\frac{1}{2}\)

Question 11.
Population of a village is 5000. Population increases at the rate of 2 % every year. What will be the population of the village after 10 years?
Answer:
Population of a village Is 5000.
∴ a = 5000
Population increases at the rate of 2 % every year.
The population after 10 years = T₁₁
Now, T_n = ar^n-1
Putting n = 11; a = 5000; r = 1.02.

T₁₁ = 5000(1.02)^11-1
= 5000 (1.02)¹⁰
= 5000(1.219)
= 6095

(1.02)¹⁰
=AL[10 log 1.021]
= AL[10 × 0.0086)
= AL [0.086]
= 1.219

Question 12.
A car depreciates at the rate of 10 % every year. If the cost price of the car is ₹ 5,00,000, what will be the value of the car after 6 years?
Answer:
The cost price of the car is ₹ 5,00,000.
∴ a = 5,00,000
The value of the car depreciates at the rate of 10 % every year.
∴ r = \(\frac{100-10}{100}=\frac{90}{100}\) = 0.9

The value of the car after 6 years = T₇
Now, T_n = ar^n-1
Putting n = 7; a = 5,00,000; r = 0.9,
∴ T₇ = 5,00,000 (0.9)^7-1
= 5,00,000(0.9)⁶
= 5,00,000(0.531441)
= 2.65,720.50
Hence, the value of the car after 6 years will be ₹ 2,65,720.50.