GSEB Solutions Class 12 Chemistry Chapter 4 રાસાયણિક ગતિકી

Gujarat Board GSEB Textbook Solutions Class 12 Chemistry Chapter 4 રાસાયણિક ગતિકી Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Chemistry Chapter 4 રાસાયણિક ગતિકી

GSEB Class 12 Chemistry રાસાયણિક ગતિકી Text Book Questions and Answers

પ્રશ્ન 1.
નીચેની પ્રક્રિયાઓ માટે વેગ અભિવ્યક્તિ (રજૂઆત) પરથી તેમના પ્રક્રિયાક્રમ અને વેગ અચળાંકના પરિમાણો નક્કી કરોઃ
(i) 3NO_(g) → N₂O_(g) વેગ = k[NO]²
(ii) H₂O_2(aq) + 3I^–_(aq) + 2H⁺_(aq) → 2H₂O_(l) + I^–₃ વેગ = k[H₂O₂p][I^–]
(iii) CH₃CHO_(g) → CH_4(g) + CO_(g) વેગ = k\(\left[\mathrm{CH}_3 \mathrm{CHO}\right]^{\frac{3}{2}}\)
(iv) C₂H₅Cl_(g) → C₂H_4(g) + HCl_(g) વેગ = [C₂H₅Cl]
ઉત્તર:
(i) આપેલ પ્રક્રિયા : 3NO_(g) → N₂O_(g)
પ્રક્રિયાવેગ = k [NO]² આપેલ છે.
∴ પ્રક્રિયાનો ક્રમ = (ઘાત) = 2
વેગ અચળાંકનું પરિમાણ :
પ્રક્રિયાનો વેગ = k [NO]²

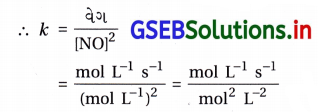
= mol^-1 L¹ s^-1
= L mol^-1 s^-1
હંમેશાં દ્વિતીય ક્રમની પ્રક્રિયાવેગ અચળાંકનો એકમ mol^-1 L s^-1 હોય છે.
હંમેશાં પ્રક્રિયાવેગનો એકમ mol L^-1 s^-1

(ii) આપેલ પ્રક્રિયા : H₂O_2(aq) + 3I^–_(aq) → 2H₂O_(l) + I^–₃
પ્રક્રિયાનો વેગ = k [H₂O₂] [I]
જેથી H₂O₂ ના સાપેક્ષ પ્રક્રિયાક્રમ = 1
I^– ના સાપેક્ષ પ્રક્રિયાક્રમ = 1
∴ એકંદર પ્રક્રિયાક્રમ = I + I = 2
k (પ્રક્રિયાવેગ અચળાંક)નું પરિમાણ :
પ્રક્રિયાવેગ = k [H₂O₂] [I^–]

mol^-1 L⁺¹ s^-1

(iii) આપેલ પ્રક્રિયા : CH₃CHO_(g) → CH_4(g) + CO_(g)
આ પ્રક્રિયાનો વેગ k = \(\left[\mathrm{CH}_3 \mathrm{CHO}\right]^{\frac{3}{2}}\)
આ પ્રક્રિયાનો ક્રમ = પ્રક્રિયાવેગ સમીકરણમાં પ્રક્રિયકની ઘાત
= \(\frac{3}{2}\)
પ્રક્રિયાના વેગનું પરિમાણ એટલે k નું પરિમાણ :

(iv) આપેલી પ્રક્રિયા : C₂H₅Cl_(g) → C₂H_4(g) + HCl_(g)
અને પ્રક્રિયાવેગ (r) = k [C₂H₅Cl]
પ્રક્રિયાનો ક્રમ (n) = (વેગ સમીકરણમાં પ્રક્રિયકોની ઘાતનો સરવાળો) = 1
પ્રક્રિયાના વેગનું અચળાંક k નું પરિમાણ :

પ્રશ્ન 2.
પ્રક્રિયા 2A + B → A₂ B માટે વેગ = k[A] [B]² છે. જેમાં k = 2.0 × 10^-6 mol^-2 L² s^-1 છે. જ્યારે [A] = 0.1 mol L^-1, B = 0.2 mol L^-1 હોય ત્યારે પ્રક્રિયાનો પ્રારંભિક વેગ ગણો. [A] ઘટીને 0.06 mol L^-1 થાય પછી પ્રક્રિયાનો વેગ ગણો.
ઉત્તર:
આપેલી પ્રક્રિયા : 2A + B → A₂B
પ્રક્રિયાના વેગનું સમીકરણ r = k[A] [B]²
જ્યાં, k = 2.0 × 10^-6 mol^-2 L² s^-1

(i) પ્રારંભમાં વેગ = r₁
પ્રારંભમાં [A] = 0.1 mol L^-1
[B] = 0.2 mol L^-1
∴ r₁ = (2.0 × 10^-6 mol^-2 L² s^-1) (0.1 mol L^-1) (0.2 mol L^-1)²
= 8 × 10^-9 mol L^-1 s^-14 ………. (i)

(ii) [A] = 0.06 mol L^-1 થાય ત્યારે વેગ r₂ : જ્યાં, r₂ = k [A] [B]²

A ની સાંદ્રતામાં ઘટાડો
0.06 = (0.1 – 2x)M
∴ (2x) = (0.1 – 0.06)M
∴ 2x = 0.04M
∴ x = 0.02M

B સંતુલને
= (0.2 – x)M
= (0.2 – 0.02)M
= 0.18M
∴ r₂ = k [A] [B]²
= (2.0 × 10^-6, mol^-2 L² S^-1) (0.06 mol L^-1) × (0.18 mol L^-1)²
= 3.888 × 10^-9 mol L^-1 s^-1

પ્રશ્ન 3.
NH₃ નું પ્લેટિનમની સપાટી પર વિઘટન શૂન્ય ક્રમની પ્રક્રિયા છે. જો k = 2.5 × 10^-4 mol^-1 L s^-1 હોય, તો N₂ અને H₂ ના નીપજના વેગ કેટલા હશે ?
ઉત્તર:
NH₃ ના વિઘટનની પ્રક્રિયા નીચે પ્રમાણે થાય.
2NH_3(g) → N_2(g) + 3H_2(g)
k = 2.5 × 10^-4 mol L^-1 s^-1
પ્રક્રિયા શૂન્ય ક્રમની છે.
પ્રક્રિયાનો વેગ = \(-\frac{1}{2} \frac{d\left[\mathrm{NH}_3\right]}{d t}=\frac{d\left[\mathrm{~N}_2\right]}{d t}=\frac{1}{3} \frac{d\left[\mathrm{H}_2\right]}{d t}\)
ય ક્રમની પ્રક્રિયા છે, હોવાથી
N₂ બનાવવાનો વેગ = \(\frac{d\left[\mathrm{~N}_2\right]^0}{d t}\) = k
= 2.5 × 10^-4 mol L^-1 s^-1
H₂ બનાવવાનો વેગ = k = \(\frac{1}{3} \frac{d\left[\mathrm{H}_2\right]^0}{d t}\) = 2.5 × 10^-4 = k
∴ \(\frac{d\left[\mathrm{H}_2\right]}{d t}\) = 3 × 2.5 × 10^-4
= 7.5 × 10^-4 mol L^-1 s^-1

પ્રશ્ન 4.
ડાયમિથાઈલ ઈથરનું વિઘટન CH₄ H₂ અને CO માંની બનાવટમાં પરિણમે છે અને પ્રક્રિયાવેગ આ પ્રમાણે આપી શકાય છે.
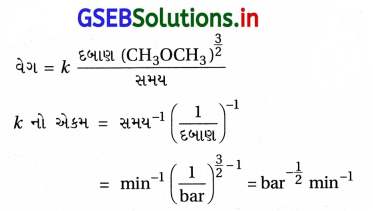
વેગ = k\(\left[\mathrm{CH}_3 \mathrm{OCH}_3\right]^{\frac{3}{2}}\)
પ્રક્રિયાનો વેગ બંધ પાત્રમાં દબાણનો વધારો કરીને અનુસરી (કરી) શકાય છે. જેથી વેગ અચળાંક ડાયમિથાઈલના આંશિક દબાણમાં અભિવ્યક્ત કરી શકાય.
વેગ = k \(\left(p_{\mathrm{CH}_3 \mathrm{OCH}_3}\right)^{\frac{3}{2}}\)
જો દબાણ bar અને સમય મિનિટમાં માપવામાં આવે, તો વેગ અને વેગ અચળાંકના એકમો શું હશે ?
ઉત્તર:
જ્યાં, દબાણ bar માં અને સમય મિનિટમાં છે.
∴ વેગનો એકમ = bar min^-1

પ્રશ્ન 5.
રાસાયણિક પ્રક્રિયાના વેગને અસર કરતાં પરિબળો જણાવો.
ઉત્તર:
રાસાયણિક પ્રક્રિયાના વેગ નીચેના પરિબળોની ઉપર આધાર રાખે છે.
(i) પ્રક્રિયકોની સાંદ્રતા
(ii) નીપજોની સાંદ્રતા
(iii) તાપમાન
(iv) ઉદ્દીપક
(v) પ્રક્રિયકો અને નીપજોની પ્રકૃતિ
(vi) સપાટીનું ક્ષેત્રફળ વગેરે…

પ્રશ્ન 6.
એક પ્રક્રિયા પ્રક્રિયકના સંદર્ભમાં દ્વિતીય ક્રમની છે. પ્રક્રિયાનો વેગ કેવી રીતે અસર પામશે ? જો પ્રક્રિયકની સાંદ્રતા (i) બમણી કરવામાં આવે. (ii) અડધી કરવામાં આવે તો.
ઉત્તર:
(i) દ્વિતીય ક્રમની પ્રક્રિયામાં પ્રક્રિયકની સાંદ્રતા બમણી કરાય તો વેગ ૪ ઉપર થતી અસર R → P પ્રક્રિયા દ્વિતીય ક્રમની હોય તો વેગ r₁ = k [R]²
હવે પ્રક્રિયક Rની સાંદ્રતા બમણી કરવાથી વેગ r₂ તો,
r₂ = k[2R]² = 4k [R]²
∴ \(\frac{r_2}{r_1}=\frac{4 k[\mathrm{R}]^2}{k[\mathrm{R}]^2}\) = 4
માટે દ્વિતીય ક્રમની પ્રક્રિયામાં પ્રક્રિયકની સાંદ્રતા બમણી કરવાથી વેગ 4 ગણો થશે.

(ii) દ્વિતીય ક્રમની પ્રક્રિયાના પ્રક્રિયકની સાંદ્રતા અડધી કરીએ તો,
પ્રારંભમાં વેગ = r₁ = k[R]²
અંતિમ વેગ = r₂ = k[latex]\frac{\mathrm{R}}{2}[/latex]²
∴ r₂ = \(\frac{k[\mathrm{R}]^2}{4}\)
∴ \(\frac{r_2}{r_1}=\frac{k[\mathrm{R}]^2}{4} \times \frac{1}{k[\mathrm{R}]^2}=\frac{1}{4}\)
જેથી દ્વિતીય ક્રમની પ્રક્રિયામાં પ્રક્રિયકની સાંદ્રતા અડધી કરવાથી તે પ્રક્રિયાનો વેગ ચોથા ભાગનો થાય છે.

પ્રશ્ન 7.
પ્રક્રિયાના વેગ અચળાંક પર તાપમાનની શું અસર છે ? તાપમાનની આ અસર વેગ અચળાંક પર જથ્થાત્મક રીતે (quantitatively) કેવી રીતે રજૂ કરી શકાય ?
ઉત્તર:

• એવું જાણવા મળે કે, રાસાયણિક પ્રક્રિયા માટે 10°C તાપમાનનો વધારો કરવાથી વેગ અચળાંક લગભગ બમણો થાય છે.
• સ્વિડીશ રસાયણશાસ્ત્રી આર્હેનિયસ પ્રમાણે તાપમાનની વેગ અચળાંક ઉપર જથ્થાત્મક રીતે થતી અસર નીચેના સમીકરણથી રજૂ કરાય છે.
  k = A \(e^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}}\)
• જ્યાં A = આર્હોનિયસ અવયવ અથવા આવૃત્તિ અવયવ તેને પૂર્વ ઘાતાંક અવયવ પણ કહે છે.
  R = વાયુ અચળાંક
  E_a = સક્રિયકરણ ઊર્જા જૂલ/મોલમાં

પ્રશ્ન 8.
પાણીમાં આભાસી પ્રથમ ક્રમની પ્રક્રિયામાં નીચેના પરિણામો મળ્યાં છે :

30 અને 60 સેકન્ડ વચ્ચેના સમયગાળાનો સરેરાશ પ્રક્રિયાવેગ ગણો.
ઉત્તર:
પ્રક્રિયા એસ્ટરનું પાણીમાં જળવિભાજનની છે અને તે આભાસી પ્રથમ ક્રમની છે.

30 અને 60 સેકન્ડ વચ્ચેના સમયગાળાનો સરેરાશ પ્રક્રિયાવેગ ગણવા.

જ્યાં C₂ = 60s પછીની સાંદ્રતા = 0.17
C₁ 30s પછીની સાંદ્રતા = 0.31
∴ r_{(30 – 60)s} = –\(\frac{(0.17-0.31) \mathrm{mol} \mathrm{L}^{-1}}{(60-30) \mathrm{s}}\)
= \(\frac{0.14}{30}\)
= 4.6667 × 10^-3 mol L^-1 s^-1

પ્રશ્ન 9.
એક પ્રક્રિયા Aના સંદર્ભમાં પ્રથમ ક્રમની છે અને Bના સંદર્ભમાં દ્વિતીય ક્રમની છે :
(i) વિકલનીય વેગ સમીકરણ લખો.
(ii) Bની સાંદ્રતા ત્રણ ગણી વધારવામાં આવે, તો વેગ કેવી રીતે અસર પામશે ?
(iii) જો A અને B બંનેની સાંદ્રતા બમણી કરવામાં આવે, તો વેગ કેવી રીતે અસર પામશે ?
ઉત્તર:
પ્રક્રિયા : A + B → P
પ્રક્રિયાનો A ના સંદર્ભમાં ક્રમ = 1
B ના સંદર્ભમાં ક્રમ = 2
∴ કુલ પ્રક્રિયાક્રમ = 1 + 2 = 3

(i) પ્રક્રિયાના વિકલન વેગનું સમીકરણ નીચે પ્રમાણે :
\(\frac{d[\mathrm{R}]}{d t}\) = k[A]¹ [B]²
ટૂંકમાં, r = [A]¹ [B]²

(ii) Bની સાંદ્રતા 3 ગણી કરવાથી વેગ ઉપર થતી અસર :
પ્રારંભમાં પ્રક્રિયાવેગ r₁ = k [A]¹ [B]²
જો Bની સાંદ્રતા ત્રણ ગણી કરવામાં આવે તો સાંદ્રતા = 3B
અને r₂ = k [A]¹ [3B]² = 9k [A]¹ [B]³
∴ વેગ નવ ગણો થાય છે.

(iii) A અને B બંનેની સાંદ્રતા બમણી કરતાં વેગ :
Aની સાંદ્રતા બમણી = 2A
Bની સાંદ્રતા બમણી = 2B
જેથી r₃ = k [2A]¹ [2B]²
= k 2[A]² × 4[B]²
= 8k [A]² [B]²
∴ વેગ 8 ગણો થશે.
(નોંધ : ફક્ત Bની સાંદ્રતા બમણી કરતાં વેગ બમણો થશે.)

પ્રશ્ન 10.
A અને B વચ્ચેની પ્રક્રિયામાં પ્રારંભિક પ્રક્રિયાવેગ (r₀)A અને Bની જુદી જુદી સાંદ્રતાએ માપવામાં આવ્યા હતા. જે નીચે આપેલા છે :

A/mol L-1	0.20	0.20	0.40
B/mol L-1	0.30	0.10	0.05
r0 mol-1 s-1	5.07 × 10-5	5.07 × 10-5	1.43 × 10-4

A અને Bના સંદર્ભમાં પ્રક્રિયાક્રમ શું હશે ?
ઉત્તર:

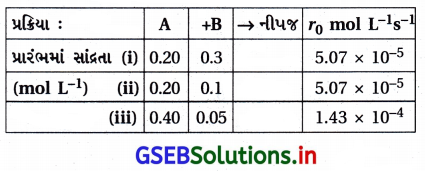
ધારો કે Aના સાપેક્ષમાં પ્રક્રિયાક્રમ = x અને Bના સાપેક્ષમાં
પ્રક્રિયાક્રમ = y તો
પ્રક્રિયાનો વેગ = k [A]^x [B]^y
જેથી r₁ = k (0.20)^x (0.3)^y = 5.07 × 10^-5
તથા r₂ = k (0.20)^x (0.1)^y = 5.07 × 10^-5
અને r₃ = k (0.40)^x (0.05)^y = 1.43 × 10^-4

yની ગણતરી :
જેથી \(\frac{r_1}{r_2}=\frac{k(0.20)^x(0.3)^y}{k(0.20)^x(0.1)^y}=\frac{5.07 \times 10^{-5}}{5.07 \times 10^{-5}}\)
∴ \(\frac{r_1}{r_2}\) = (3)^y = 1
∴ 3^y = 1 જેથી y = 0 થાય.
કારણ કે 3⁰ = 1 થાય છે.

x ની ગણતરી :
સમી. (i) અને (iii) માં yનું મૂલ્ય શૂન્ય મૂકવાથી
r₁ = k(0.20)^x (0.3)^y = k(0.2)^x (0.3)^O
∴ r₁ = k(0.2)^x = 5.07 × 10^-5
r_iii = k(0.4)^x (0.05)^O
∴ 1.43. 10^-4 = k(0.4)^x
∴ r_iii = 1.43 × 10^-4 = k(0.4)^x
∴ \(\frac{r_{\text {(iii) }}}{r_{\text {(i) }}}=\frac{1.43 \times 10^{-4}}{5.07 \times 10^{-5}}=\frac{k(0.4)^x}{k(0.2)^x}\)
∴ 2.8205 = (\(\frac{0.4}{0.2}\))^x = 2^x
જેથી log 2.8205 = x log 2
∴ 0.4503 x × 0.3010
∴ x = \(\frac{0.4503}{0.3010}\)
= 1.5
જેથી x ના સંદર્ભમાં પ્રક્રિયાક્રમ = 1.5

પ્રશ્ન 11.
2A + B → C + D પ્રક્રિયાના ગતિકી અભ્યાસ દરમિયાન નીચેના પરિણામો મળ્યાં છે : [ઑગસ્ટ-2020]

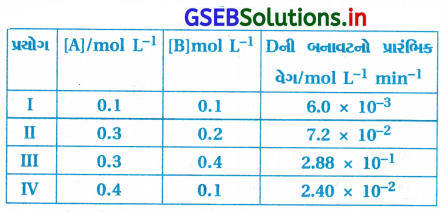
પ્રક્રિયાનો વેગ નિયમ અને વેગ અચળાંક નક્કી કરો.
ઉત્તર:
પ્રક્રિયા : 2A + B → C + D

પ્રયોગ	[A]/mol L-1	[B]mol L-1]	Dની બનાવટનો પ્રારંભિક વેગ/mol L-1 min-1
I	0.1	0.1	6.0 × 10-3
IV	0.4	0.1	2.4 × 10-2

Aના સંદર્ભમાં પ્રક્રિયાક્રમ નક્કી કરવો :
વેગ = k[A]^x [B]^y
જેથી r₁ = k(0.1)^x (0.1)^y = 6.0 × 10^-3
r₄ = k(0.4)^x (0.1)^y = 2.4 × 10^-2
∴ \(\frac{r_4}{r_1}=\frac{k(0.4)^x(0.1)^y}{k(0.1)^x(0.1)^y}=\left(\frac{24 \times 10^{-2}}{6.0 \times 10^{-3}}\right)\)
∴ (4.0)^x = 4.0
જો x = 1 તો (4.0)^x = 4
∴ Aના સંદર્ભમાં પ્રક્રિયાક્રમ
(i) અને (iv)માં Bની સાંદ્રતા સમાન 0.1 M સાંદ્રતા 0.1માંથી 0.4 mol^-1 થાય છે ત્યારે 6.4 × 10^-3માંથી 24 × 10^-3 થાય છે.
∴ વેગ ∝ A જેથી A માટે પ્રક્રિયાક્રમ = 1
Bના સંદર્ભમાં પ્રક્રિયાનો ક્રમ નક્કી કરવો :

આ બંનેમાં Aની સાંદ્રતા સમાન છે.
Bની સાંદ્રતા 0.2માંથી 0.4 mol^-1 એટલે કે બમણી થાય.
જ્યારે વેગ \(\frac{r_3}{r_2}=\frac{2.88 \times 10^{-1}}{7.2 \times 10^{-2}}\) = 4(વેગ ચાર ગણો થાય.)
∴ વેગ ∝ [B]²
∴ [B] ના સંદર્ભમાં પ્રક્રિયાક્રમ = 2
∴ વેગ નિયમ = k [A] [B]²
વેગ અચળાંક ની ગણતરી :
પ્રયોગ (I)માં વેગ = k[A]^x [B]^y = 6.0 × 10^-3
∴ k(0.1)¹ × (0.1)² = 6.0 × 10^-3
∴ k = \(\frac{6.0 \times 10^{-3}}{0.1 \times 0.01}=\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~min}^{-1}}{\left(\mathrm{~mol} \mathrm{~L}^{-1}\right)\left(\mathrm{mol} \mathrm{L}^{-1}\right)^2}\)
∴ વેગ અચળાંક k = 6.0 mol^-2 L⁺² min^-1
આ જ મૂલ્યો પ્રયોગ II, III અને IVમાંથી મળશે.

પ્રશ્ન 12.
A અને B વચ્ચેની પ્રક્રિયા Aના સંદર્ભમાં પ્રથમ ક્રમની છે અને Bના સંદર્ભમાં શૂન્ય ક્રમની છે. નીચેના કોષ્ટકમાં ખાલી જગ્યાની પૂર્તિ કરો.

પ્રયોગ	[A]/mol L-1	[B]mol L-1	પ્રારંભિક વેગ / mol L-1 min-1
I	0.1	0.1	2.0 × 10-2
II	–	0.2	4.0 × 10-2
III	0.4	0.4	–
IV	–	0.2	2.0 × 10-2

ઉત્તર:

• પ્રક્રિયા : A + B → નીપજ
  પ્રક્રિયાક્રમ : Aના સંદર્ભમાં 1
  પ્રક્રિયાક્રમ : Bના સંદર્ભમાં શૂન્ય
  ∴ પ્રક્રિયાવેગ = r = k[A]¹[B]⁰
  ∴ r = [A] અને k = \(\frac{r}{[\mathrm{~A}]}\)
• પ્રયોગ Iમાં ની ગણતરી :
  k = \(\frac{r}{[\mathrm{~A}]}=\frac{2.0 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{0.1 \mathrm{~mol} \mathrm{~L}^{-1}}\)
  = 0.2 min^-1 ……………… (I)
• પ્રયોગ (II)માં Aની ગણતરી :
  r = k[A]
  ∴ 4.0 × 10^-2 = 0.2 [A]
  ∴ [A] = \(\frac{4.0 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{0.2 \mathrm{~min}^{-1}}\)
  = 0.2 mol L^-1 …………. (II)
• પ્રયોગ (III)માં પ્રારંભિક વેગની ગણતરી :
  વેગ = k[A]
  = 0.2 min^-1 (0.4 mol L^-1)
  = 0.08 mol L^-1 mn^-1 ………. (III)
• પ્રયોગ (IV)માં [A]ની ગણતરી :
  r = [A]
  ∴ 2.0 × 10^-2 mol L^-1 min^-1 = 0.2 min^-1 [A]
  ∴ [A] = \(\frac{2.0 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{0.2 \mathrm{~min}^{-1}}\)
  = 0.1 mol L^-1 ………. (IV)

પ્રશ્ન 13.
પ્રથમ ક્રમની પ્રક્રિયાના તેમના નીચે આપેલા વેગ અચળાંક પરથી પ્રથમ ક્રમની પ્રક્રિયાના અર્ધઆયુષ્ય (સમય) ગણો :
(i) 200 s^-1
(ii) 2 min^-1
(iii) 4 years^-1
ઉત્તર:
પ્રથમ ક્રમની કોઈ પણ પ્રક્રિયા માટે t_1/2 = \(\frac{0.693}{k}\)
(i) t_1/2(200 s) = \(\frac{0.693}{200 \mathrm{~s}}\) જ્યાં, k = 200^-1s
= 3.465 × 10^-3 s^-1

(ii) t_1/2 (2 min) = \(\frac{0.693}{2 \mathrm{~min}}\)
= 0.3465 min^-1

(iii) t_1/2 (4 year) = \(\frac{0.693}{4 \text { year }}\)
= 0.17325 year

પ્રશ્ન 14.
¹⁴Cનો રેડિયોએક્ટિવ ક્ષયનો અર્ધઆયુષ્ય સમય 5730 વર્ષ છે. એક પુરાતાત્વિક કૃત્રિમવસ્તુ (artifact) જે જીવિત વૃક્ષમાં મળેલા ¹⁴Cના માત્ર 80% કાષ્ટ ધરાવે છે. નમૂનાનું આયુષ્ય (ઉંમર) અંદાજો.
ઉત્તર:

• ¹⁴C નો અર્ધઆયુષ્ય સમય t_1/2 = 5730 વર્ષ
  …………………. સમય પછીથી 80 ¹⁴C છે.
• જેથી જો પ્રારંભમાં ¹⁴C₀ = [R]₀
  તો t સમય પછીથી ¹⁴C = [R]_t = 80% [R]₀
  = 0.8 [R]₀
• રેડિયોઍક્ટિવ ક્ષય તે બધી જ પ્રથમ ક્રમની પ્રક્રિયા છે.
  જેથી t_1/2 = \(\frac{0.693}{k}\) (પણ tt_1/2 = 5730 વર્ષ)
  ∴ k = \(\frac{0.693}{5730}\) વર્ષ
• પ્રથમ ક્રમની પ્રક્રિયાઓ માટે,

= 1845.2 વર્ષ

પ્રશ્ન 15.
N₂O₅ના વાયુમય કલામાં 318 K તાપમાને વિઘટનની [2N₂O₅ → 4NO₂ + O₂] પ્રાયોગિક માહિતી નીચે આપેલ છે :

(i) [N₂O₅] વિરુદ્ધ t આલેખ દોરો.
(ii) પ્રક્રિયા માટેનો અર્ધઆયુષ્ય સમય શોધો.
(iii) log [N₂O₅] અને t વચ્ચેનો આલેખ દોરો.
(iv) વેગનિયમ શું હશે ?
(v) વેગ અચળાંક ગણો.
(vi) k ઉપરથી અર્ધઆયુષ્ય સમય ગણો અને (ii) સાથે સરખાવો.
ઉત્તર:
(i) પ્રક્રિયા : 2N₂O₅ → 4NO₂ + O₂
[N₂O₅] વિરુદ્ધ tનો આલેખ નીચે પ્રમાણે છે.
ઢાળ = \(\frac{\Delta \log \left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta l}\)

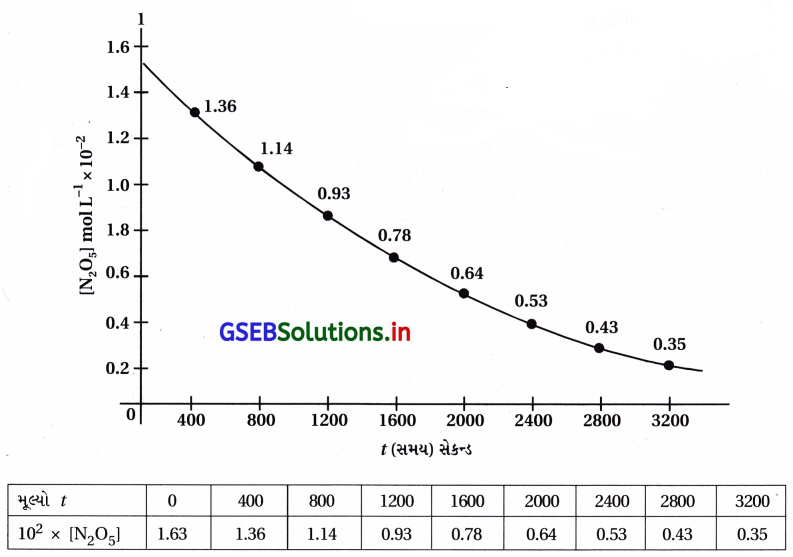
(ii) પ્રક્રિયાના અર્ધઆયુષ્ય સમય (t_1/2 ની ગણતરી :
સમય = 0 થી 3200 સેકન્ડ
∴ t_1/2 = 1600 s
t = 0 સમયે [N₂O₅] = 1.63 × 10^-2 mol L^-1
જેથી અડધું સાંદ્રણ = \(\frac{1.63}{2}\) = 0.815 × 10^-2 mol L^-1
અને આલેખમાંથી અડધું સાંદ્રણ 0.815 × 10^-2 mol L^-1 થવાનો આલેખમાંથી સમય = 1402 s મળે છે.
∴ t_1/2 = 1402 s

(iii) log [N₂O₅] અને સમય t વચ્ચેનો આલેખ :

t(s)	[N2O5] mol L-1	log [N2O5]
0	1.63 × 10-2	– 2 + 0.2122 = – 1.7888 = – 1.79
400	1.36 × 10-2	– 2 + 0.1235 = – 1.866 = – 1.87
800	1.14 × 10-2	– 2 + 0.0569 = – 1.943 = – 1.94
1200	0.93 × 10-2	– 2 + 0.0315 = – 2.0315 = – 2.02
1600	0.78 × 10-2	– 2 + 0.1078 = – 2.1078 = – 2.11
2000	0.64 × 10-2	– 2.1938 = – 2.19
2400	0.13 × 10-2	– 2.2757 = – 2.28
2800	0.43 × 10-2	– 2.3665 = 2.37
3200	0.35 × 10-2	– 2.4559 = – 2.46

નોંધ : આલેખ સુરેખ અને ઋણ ઢાળ = – \(\frac{k}{2.303}\)

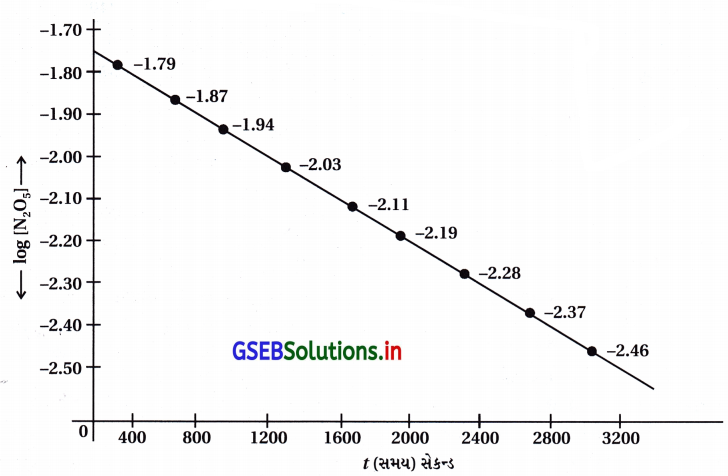
(iv) વેગ નિયમ તારવવો : log [N₂O₅] → સમયનો આલેખ સુરેખ છે; જે સૂચવે છે કે આ N₂O₅ના વિઘટનની પ્રક્રિયા પ્રથમ ક્રમની છે.
પ્રક્રિયા : 2N₂O₅ → 4NO₂ + O₂
∴ વેગ = k[N₂O₅]

(v) વેગ અચળાંક (K)ની ગણતરી :
આલેખની રીતે : log [N₂O₅] → tના આલેખમાંથી
રેખાનો ઢાળ = – \(\frac{k}{2.303}\)
∴ k – ઢાળ × 2.303
= – \(\frac{2.46-(-1.79)}{(3200-0) \mathrm{s}}\) × 2.303
= – \(\frac{-0.67}{3200}\) × 2.303
= 4.8219 × 10^-4 s^-1 = 4.82 × 10^-4 s^-1

અથવા

સૂત્ર ઉપરથી ત્ની ગણતરી : k = \(\frac{2.303}{\Delta t}\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]_t}\)
જ્યાં,Δt = 3200 – 0 = 3200 s
[R]₀ = શૂન્ય સમયની સાંદ્રતા = 1.63 × 10^-2 mol L^-1
[R]_t = 3200 સેકન્ડે સાંદ્રતા = 0.35 × 10^-2 mol L^-1
∴ log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]_t}=\frac{1.63 \times 10^{-2}}{0.35 \times 10^{-2}}\)
= log 4.6571 = 0.6681
∴ k = \(\frac{2.303}{3200}\) × 0.6681 = 4.8083 × 10^-4
= 4.81 × 10^-4 s^-1

(vi) t_1/2 ની ગણતરી :
t_1/2 = \(\frac{0.693}{k}=\frac{0.693}{4.8219 \times 10^{-4} \mathrm{~s}^{-1}}\)
= 0.1437 × 10⁴ s = 1.437 × 10³ s = 1437 s
અર્ધઆયુષ્ય સમય : 1437 s < 1402 s

પ્રશ્ન 16.
પ્રથમ ક્રમની પ્રક્રિયા માટે વેગ અચળાંક 60 s^-1 છે. પ્રક્રિયકની પ્રારંભિક સાંદ્રતાથી તેના \(\frac{1}{6}\) ભાગના મૂલ્ય જેટલી સાંદ્રતા ઘટીને થવા માટે તે કેટલો સમય લેશે ?
ઉત્તર:

• પ્રક્રિયાનો ક્રમ = 1
  પ્રક્રિયાનો વેગ અચળાંક k = 60 s^-1
  ધારો કે પ્રારંભિક સાંદ્રતા = [R]₀ mol L^-1
  t સમય પછીથી સાંદ્રતા = \(\frac{1}{6}\) પ્રારંભિક સાંદ્રતા
  ∴ [R]_t = \(\frac{1}{6}\) [R]₀ mol L^-1
• પ્રથમ ક્રમની પ્રક્રિયા માટે,
  t = \(\frac{2.303}{k}\) log \(\frac{[\mathrm{R}]_0 6}{[\mathrm{R}]_0}\)
  = \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) × log 6 = \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) × 0.7782
  = 2.9868 × 10^-2 s
  નોંધ : જો t સમય પછીથી સાંદ્રતા \(\frac{1}{16}\) હોય તો,
  t = \(\frac{2.303}{k}\) log \(\frac{[\mathrm{R}]_0 \times 16}{[\mathrm{R}]_0}\)
  = \(\frac{2.303}{k}\) log 16 = \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) × 1.2041
  = 4.62 × 10^-2 s
  નોંધ : અહીં, \(\frac{1}{16}\) પ્રમાણેની ગણતરી અંગ્રેજીના પુસ્તક પ્રમાણે છે.

પ્રશ્ન 17.
કેન્દ્રીય વિસ્ફોટન દરમિયાન નીપજોમાંની એક ⁹⁰Sr છે. જેનું અર્ધઆયુષ્ય 28.1 વર્ષ છે. જો તે જ સમયે તાજા જન્મેલા બાળકનાં હાડકાંમાં 1 μg ⁹⁰Sr કેલ્શિયમને બદલે શોષાયેલ હોય, તો તે બાળકમાં જો બીજી કોઈ ચયાપચયની ક્રિયાથી ⁹⁰Sr ગુમાવાયું ન હોય, તો 10 વર્ષ અને 60 વર્ષના અંતે તેના શરીરમાં કેટલું ⁹⁰Sr રહ્યું હશે ?
ઉત્તર:

• કેન્દ્રીય વિખંડન તે પ્રથમ ક્રમની પ્રક્રિયા છે.
  અર્ધઆયુષ્ય સમય t_1/2 = 28.1 વર્ષ
  તાજા જન્મેલા બાળકમાં 1 μg ⁹⁰Sr
  ∴ [R]₀ = 1 μg
  સમય t₁ = 10 વર્ષ પછી તો [R]_t1 = x [R]_t1 = x μg તથા
  સમય t₂ = 60 વર્ષ પછી તો [R]_t2 = y μg
• વિખંડનની પ્રક્રિયાનો અચળાંક = k જો પ્રક્રિયા પ્રથમ ક્રમની હોય તો,

∴ \(\frac{1}{x}\) = 1.2794
∴ x = 0.7816 μg ⁹⁰Sr બાકી રહ્યું હશે.

• t = 60 વર્ષ પછીથી ⁹⁰S = y μg ધારતાં,
  t = \(\frac{2.303}{k}\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]_t}\)
  ∴ 60 = \(\frac{2.303}{0.024662}\) log \(\frac{1}{y}\)
  \(\frac{60 \times 0.024662}{2.303}\) = log 1 – log y
  ∴ 0.6425 = 0 – log y = – log y
  ∴ log y = – 0.6425
  ∴ y = Antilog (-0.6425) = 0.228 μg ⁹⁰Sr બાકી હશે.

પ્રશ્ન 18.
પ્રથમ ક્રમની પ્રક્રિયા માટે દર્શાવો કે 99% પ્રક્રિયા પૂર્ણ થવા માટે જરૂરી સમય પ્રક્રિયા 90% પૂરી થવા માટે જરૂરી સમય કરતાં બમણો છે.
ઉત્તર:
(a) 90% પ્રક્રિયા પૂર્ણ થતાં t (90%)ની ગણતરી :
અહીં, 90% પ્રક્રિયા પૂર્ણ થાય છે. ∴ 10% બાકી રહેતી સાંદ્રતા જો પ્રારંભની સાંદ્રતા [R]₀ તો 90% પૂર્ણ થયા પછીની

(b) 99% પ્રક્રિયા પૂર્ણ થતાં t (99%)ની ગણતરી : 99 % પ્રક્રિયા પૂર્ણ થાય તો 1% પ્રક્રિયક બાકી રહે જેથી જો પ્રારંભની સાંદ્રતા = [R]₀, તો 99% પૂર્ણ થઈ 1% બાકી રહે ત્યારે બાકી રહેતી સાંદ્રતા = [R]_t (99)
[R]_t = [R]₀ ના 1% = \(\frac{1}{100}\) [R]₀ = 0.01 [R]₀
t_(99%) = \(\frac{2.303}{k}\) log \(\frac{[\mathrm{R}]_0}{0.01[\mathrm{R}]_0}=\frac{2.303}{k}\) × 2
∴ \(\frac{t_{99 \%}}{t_{90 \%}}=\left(\frac{2.303}{k}\right)\) × 2 × \(\left(\frac{k}{2.303}\right)=\frac{2}{1}\)
આમ પ્રક્રિયા 99% પૂર્ણ થવાનો સમય 90% પૂર્ણ થયાના સમય કરતાં બમણો છે, જો પ્રથમ ક્રમની પ્રક્રિયા હોય તો જ.

પ્રશ્ન 19.
એક પ્રથમ ક્રમની પ્રક્રિયા 30% વિઘટન માટે 40 min લે છે. t_1/2 ગણો. [ઑગસ્ટ-2020]
ઉત્તર:

• પ્રથમ ક્રમની પ્રક્રિયા છે. જેથી 30% વિઘટન પામે છે.
  ∴ જો પ્રારંભમાં સાંદ્રતા = [R]₀
• 40 મિનિટમાં પ્રક્રિયક 30% વિઘટન પામે છે, જેથી 70% બાકી રહે.
  ∴ [R]_t = [R]₀ ના 70%
  = \(\frac{70}{100}\) [R]₀ 0.7 [R]₀
• k ત્ની ગણતરી : પ્રથમ ક્રમની પ્રક્રિયા છે, જેથી

પ્રશ્ન 20.
એઝોઆઇસોપ્રોપેનનું હેક્ઝેન અને નાઇટ્રોજનમાં વિઘટન 543K તાપમાને કરવામાં આવે છે. માહિતી નીચે પ્રમાણે મળેલી છે :

t (sec)	P (mm of Hg)
0	35.0
360	54.0
720	63.0

વેગ અચળાંક ગણો.
ઉત્તર:
(a) 360 સેકન્ડ પછીથી વેગ અચળાંકની ગણતરી :

જેથી એઝોઆઇસોપ્રોપેન માટે,
[R]₀ = પ્રારંભમાં સાંદ્રતા = પ્રારંભમાં દબાણ = 35 mm = P_i
[R]_t = 360 સેકન્ડ પછી અંતિમ સાંદ્રતા = 16 mm = P_t
પ્રથમ ક્રમની પ્રક્રિયા છે.
∴ k = \(\frac{2.303}{t}\) log \(\frac{p_i}{p_t}\)
∴ k = \(\frac{2.303}{t}\) log (\(\frac{35}{16}\))
∴ k = \(\frac{2.303}{360 \mathrm{~s}}\) = 0.3399 = 2.1747 × 10^-3 s^-1

(b) 720 s પછીથી k ની ગણતરી :
t = 0 સમયે પ્રારંભિક દબાણ = P_i = 35.0 mm = [R]₀
t = 720 સમયે કુલ દબાણ = 63 mm
જે સંતુલને (35 – y) + y + y = (35 + y) = 63 mm અને
y = (63 – 35) = 28 mm
∴ [R]_t = p_t = 1 (35 – 28) = 7 mm
∴ k = \(\frac{2.303}{720 \mathrm{~s}}\) log (\(\frac{35}{7}\)) = \(\frac{2.303}{720}\) × 0.6990
= 0.0024 s^-1
સરાસરી k = \(\frac{\left(2.1747 \times 10^{-3}\right)+\left(2.4 \times 10^{-3}\right)}{2}\)
= 2.21 × 10^-3 s^-1

પ્રશ્ન 21.
અચળ કદે પ્રથમ ક્રમની SO₂Cl₂ની વિઘટન પ્રક્રિયા
SO₂Cl_2(g) → SO_2(g) + Cl_2(g) દરમિયાન નીચેની માહિતી મળેલી છે :

પ્રયોગ	સમય / s-1	કુલ દબાણ / atm
1	0	0.5
2	100	0.6

જો કુલ દબાણ 0.65 atm હોય, તો પ્રક્રિયાનો વેગ ગણો.
ઉત્તર:

∴ કુલ દબાણ P = p(SO₂Cl₂) + p(SO₂) + (Cl₂)
= (p₀ – x) + x + x
∴ કુલ દબાણ P = (P₀ + x) atm
∴ X = (P – P₀) atm
∴ P_t (SO₂Cl₂) = P₀ – x
= P₀ (P – P₀) = 2 P₀ – P
જ્યાં, P = કુલ દબાણ t સેકન્ડ, p₀ = દબાણ ૦ સેકન્ડ

પ્રયોગ-1 :
જ્યાં, t = 0 સેકન્ડ
કુલ દબાણ P = 0.5 atm = P₀
t = 100 સેકન્ડે દબાણ = 0.6 atm = p
∴ P_t (2p₀ – p) = (2(0.5) – 0.6) = 0.4 atm
∴ k = \(\frac{2.303}{t}\) log \(\frac{p_0}{p_t}=\frac{2.303}{100 \mathrm{~atm}}\) log (\(\frac{0.5 \mathrm{~atm}}{0.4 \mathrm{~atm}}\))
= \(\frac{2.303}{100 \mathrm{~atm}}\) × 0.09691
= 2.2318 × 10^-3 s^-1

પ્રયોગ-2 :
P_t = 2P₀ – p
જ્યાં,
કુલ દબાણ P = 0.65 atm
P₀ = 0.5 atm
t = 0 time
= 2[(0.5) 0.60]
= (1.0 – 0.60)
= 0.4 atm
∴ P_(SO2Cl2) = 0.4 atm
વેગ a = k × P_SO2Cl2
r = 2.2318 × 10^-3 s^-1 × 0.4 atm
r = 9.272 × 10^-4
= 9.2 × 10^-4 atm s^-1

પ્રશ્ન 22.
N₂O₅ના વિઘટનના વેગ અચળાંક જુદાં-જુદાં તાપમાને નીચે આપેલા છે :

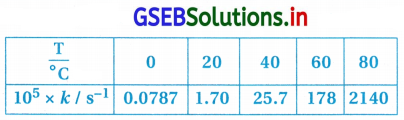
In k અને \(\frac{l}{\mathrm{~T}}\) વચ્ચે આલેખ દોરો અને A અને E_a ના મૂલ્યો ગણો. 30°C અને 50°C તાપમાને વેગ અચળાંકનું પ્રાથન કરો.
ઉત્તર:

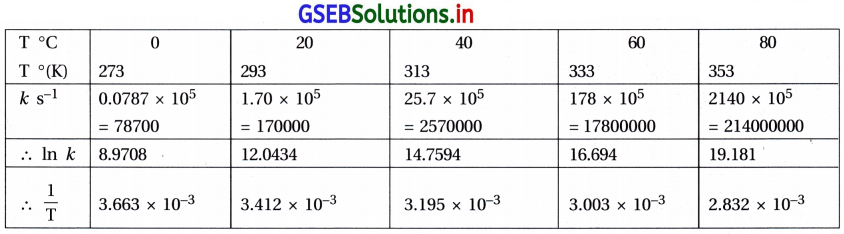
In k → \(\frac{l}{\mathrm{~T}}\) નો આલેખ નીચે મુજબ :
આલેખ ઋણ ઢાળ ધરાવતી સીધી રેખા છે.
ઢાળ = \(\frac{\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\)
જયાં R = 8.314 J K^-1 mol^-1
∴ E_a = R (- ઢાળ)
[Ink = 22.3 = આંતરછેદ]

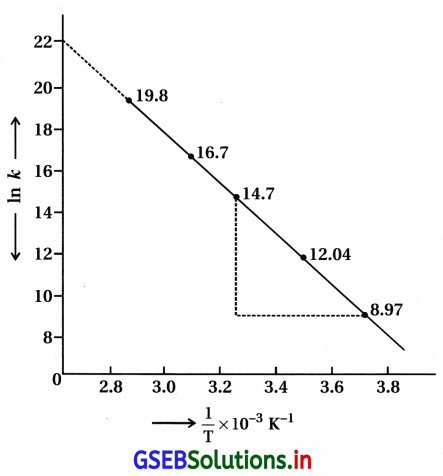
E_aના મૂલ્યની ગણતરી :
log \(\frac{\mathrm{K}_2}{\mathrm{~K}_1}=-\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\left(\frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\right)\)
ઉપર બનાવેલા કોઠામાંથી,
જયાં, T₂ = 313 K તો K₂ = 25.7 × 10⁵ s^-1
T₁ = 293 K તો K₁ = 1.70 × 10⁵ s^-1
R = 8.314 J K^-1 mol^-1

= 1.1795 × 87798.3 = 103558 J = 103558 J = 103.558 kJ
Aની ગણતરી (293 K તાપમાને) :
જયાં, T = 293 K; k = 1.7 × 10⁵
E_a = 103558 J ; R = 8.314 J K^-1 mol^-1
∴ log k = log A – \(\frac{E_a}{2.303 \mathrm{RT}}\)
∴ log (1.7 × 10⁵) = log A – \(\frac{103558}{2.303 \times 8.314 \times 293}\)
∴ 5.2304 = log A – 18.459
∴ log A = 5.2304 + 18.459 = 23.6894
∴ A = Antilog 23.6894 = 4.8910 × 10²³ s^-1
આલેખથી Aની ગણતરી : આલેખની રેખાને લંબાવતાં લગભગ
1n = 22.2 થાય ત્યાં Y- અક્ષને અડકે છે.
આંતરછેદ = 22.2 = A = 1n A
1n A = 2.303 log 22.2
∴ A = (Antilog 22.2) × 2.303
= 1.5849 × 10²² × 2.303 = 3.65 × 10²²
30° C તાપમાને ની ગણતરી :
T = 30 + 273 = 303 K
A = 4.8910 × 10²³ s^-1
log k = log A = \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
∴ log k = log 4.8910 × 10²³ – \(\frac{103558}{2.303 \times 8.314 \times 303}\)
= 123.6894 – 17.85
= 5.8394
∴ k = Antilog 5.8394 = 690875.8
= 6.909 × 10⁵ s^-1
50° C તાપમાને ની ગણતરી :
Τ = 50 + 273 = 323 K
∴ log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
= log 4.8910 × 10⁵ – \(\frac{103558}{2.303 \times 8.314 \times 323}\)
= 23.6894 – 16.7447 = 6.9447
∴ k = Antilog 6.9447 = 8.8044 × 10⁶

પ્રશ્ન 23.
546 K તાપમાને હાઇડ્રોકાર્બનના વિઘટનનો વેગ અચળાંક 2.418 × 10^-5 s^-1 છે. જો સક્રિયકરણ ઊર્જા 179.9 kJ / mol હોય, તો પૂર્વઘાતાંક (pre exponential) અવયવ (factor)નું મૂલ્ય કેટલું હશે ?
ઉત્તર:
આર્ટેનિયસ સમીકરણથી,
log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
log A = log k + \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
જ્યાં T = 546 k
k = 2.418 × 10^-5 s^-1
log k = – log 2.418 × 10^-5 = – 4.6165
E_a = 179.9 kJ = 179900 J mol^-1
A = (?)
∴ log A = – 4.6165 + \(\frac{179900}{2.303 \times 8.314 \times 546}\)
= – 4.6165 + 17.2082 = 12.5917
∴ A = Antilog 12.5917
= 3.9057 × 10¹² = 3.91 × 10¹² s^-1

પ્રશ્ન 24.
કોઈ પ્રક્રિયા A → નીપજ તરીકે ગણો જેનો = 2.0 × 10^-2 s છે. જો Aની પ્રારંભિક સાંદ્રતા 1.0 mol L^-1 હોય, તો 100 s પછી Aની શેષ સાંદ્રતા ગણો.
ઉત્તર:
પ્રક્રિયા : A → નીપજ
K = 2.0 × 10^-2 s^-1
t = 100 s
પ્રારંભિક સાંદ્રતા = [A]₀ = 1.0 mol L^-1
100 s પછી [R]_t = (?)
K નો એકમ સેકન્ડ^-1 છે.
∴ પ્રથમ ક્રમની પ્રક્રિયા હોવી જોઈએ.
K = \(\frac{2.303}{t}\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]_t}\)
∴ 2.0 × 10^-2 = \(\frac{2.303}{100 \mathrm{~s}}\) log \(\frac{(1.0)}{\log [\mathrm{R}]_t}\)
∴ \(\frac{2.0 \times 10^{-2} \times 100}{2.303}\) = log 1 – log [R]_t
∴ 0.8684 – log [R]_t
∴ log [R]_t = – 0.8684
∴ [R]_t = Antilog (1 – 0.8684) = 0.1354 mol L^-1

પ્રશ્ન 25.
સુક્રોઝ એસિડિક દ્રાવણમાં ગ્લુકોઝ અને ફ્રુક્ટોઝમાં પ્રથમ ક્રમ વેગ નિયમ પ્રમાણે વિઘટન પામે છે. જેનો t_1/2 = 3.00 કલાક છે. 8 કલાક પછી સુક્રોઝના નમૂનાનો કેટલો અંશ શેષ રહ્યો હશે ?
ઉત્તર:

પ્રક્રિયા પ્રથમ ક્રમની છે. જ્યાં, t_1/2 = 3.00 કલાક
∴ પ્રથમ ક્રમની પ્રક્રિયા હોવાથી,
k = \(\frac{0.693}{t}=\frac{0.693}{300 \mathrm{~h}}\) = 0.231 hr^-1
8 કલાક પછીથી બાકી રહેલા સુક્રોઝનો અંશ ગણવો. ધારો કે પ્રારંભમાં સુક્રોઝની સાંદ્રતા = [R]₀ mol L^-1
8 કલાક પછીથી સુક્રોઝની સાંદ્રતા = [R]_t mol L^-1

પ્રશ્ન 26.
હાઇડ્રોકાર્બનનું વિઘટન નીચેના સમીકરણને અનુસરે છે.
k = (4.5 × 10¹¹ s^-1) e^{-28000 K/T}
E_a ની ગણતરી કરો.
ઉત્તર:
k = 4.5 × 10¹¹ s^-1 e^{-28000 K/T} ……. (a)
– E_aની ગણતરી કરવી. અહીં K તે તાપમાન કૅલ્વિનમાં સૂચવે છે.
આર્ટેનિયસ પ્રમાણે,
k = Ae^-E_a/RT ……… (b)
∴ આ (a) અને (b)માં સરખામણી કરવાથી (a)માં 4.5 × 10¹¹ તે (b)નો K છે.
(a)માં e^{-28000 K/T} = (b)માં e^-E_a/RT થાય.
એટલે કે – \(\frac{\mathrm{E}_{\mathrm{a}}}{\mathrm{RT}}=-\frac{28000 \mathrm{~K}}{\mathrm{~T}}\)
∴ E_a = 28000 K × R
= 28000 K × 8.3.4 J K^-1 mol^-1
= 28000 × 8.314 J mol^-1
= 232792 J mol^-1
= 232.792 kJ mol^-1

પ્રશ્ન 27.
H₂O₂ના પ્રથમ ક્રમ પ્રમાણે વિઘટનનો વેગ અચળાંક નીચેના સમીકરણ દ્વારા દર્શાવી શકાય.
log k = 14.34 1.25 × 10⁴ K/T
આ પ્રક્રિયા માટે E_a ગણો અને કયા તાપમાને તેનો અર્ધઆયુષ્ય 256 મિનિટ થશે ?
ઉત્તર:

• E_a ની ગણતરી : પ્રથમ ક્રમની પ્રક્રિયા છે.
  પ્રક્રિયામાં H₂O₂નું વિઘટન થાય છે. આપેલું છે કે….
  log k = 14.34 – 1.25 × 10⁴ K/T …….. (a)
  log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\) (આર્મેનિયસ (b))
• (a) અને (b) સમીકરણોને સરખાવી, log k તથા 14.34 = log A સ્વીકારી દૂર કરવાથી
  \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}=\frac{1.25 \times 10^4}{\mathrm{~T}}\)k
  ∴ E_a = 1.25 × 104 k × 2.303 × 8.314 J K^-1 mol^-1
  = 2.3934 × 10⁵ J mol^-1
  = 239.34 kJ mol^-1
• t_1/2ઉપરથી વિઘટન અચળાંક kની ગણતરી :
  k = \(\frac{0.693}{t}\) જ્યાં, t_1/2 = 256 મિનિટ
  \(\frac{0.693}{256 \mathrm{~min}}\) અથવા \(\frac{0.693}{256 \times 60 \mathrm{~s}}\)
  = 2.707 × 10^-3 min^-1 અથવા 4.50 × 10^-5 s^-1
• t_1/2 થવાના તાપમાનની ગણતરી :
  આપેલું સમીકરણ : log k = 14.34 – \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
  ∴ log (4.51 × 10^-5) = 14.34 – \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
  ∴ – 4.3458 – 14.34 = – \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
  ∴ – 18.6858 = – \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
  ∴ T = \(\frac{1.25 \times 10^4 \mathrm{~K}}{18.6858}\) 668.96 k = 669 K
  (નોંધ : k = 2.707 × 10^-3 લેશો તો k = 739.3 k આવશે.)

પ્રશ્ન 28.
Aનું નીપજોમાં વિઘટનમાં 10° C તાપમાને નું મૂલ્ય k નું મૂલ્ય 4.5 × 10³ s^-1 દર્શાવે છે અને સક્રિયકરણ ઊર્જા 60 kJ mol^-1 દર્શાવે છે. કયા તાપમાને k નું મૂલ્ય 1.5 × 10⁴ s^-1 થશે ?
ઉત્તર:
પ્રક્રિયા A → નીપજો
T₁ = 10° C = 10 + 273 = 283 K અને
K₁ = 4.5 × 10³ s^-1
E_a = 60 kJ mol^-1 = 60,000 J mol^-1
જો K₂ = 1.5 × 10⁴ s^-1 તો તાપમાન T₂ = (?)
આર્હેનિયસ સમીકરણ નીચે પ્રમાણે છે.

∴ T₂ – 283 = (0.0472) T₂
∴ (T₂ – 0.0472 T₂) = 283
∴ 0.9528 T₂ = 283
∴ T₂ \(\frac{283}{0.9528}\) 297.02 K = 24.02° C

પ્રશ્ન 29.
298K તાપમાને પ્રથમ ક્રમની પ્રક્રિયાને 10% પૂર્ણ થવા જરૂરી સમય 308K તાપમાને તે જ પ્રક્રિયાને 25% પૂર્ણ થવા માટે લાગતા સમય જેટલો જ છે. જો Aનું મૂલ્ય 4 × 10¹⁰ s^-1 હોય, તો 318K તાપમાને k અને E_a ગણો.
ઉત્તર:
પ્રથમ ક્રમની પ્રક્રિયાને 10 % પૂર્ણ થવાનો સમય t₁ તાપમાન T₁
T₁ = 298 K, સમય = t₁
જો પ્રારંભની સાંદ્રતા = [R]₀ mol L^-1
પ્રક્રિયા 10% પૂર્ણ થાય જેથી 90% પ્રક્રિયક બાકી રહે.
∴ [R]_t = 0.9 [R]₀ mol L^-1
∴ log k₂₉₈ = \(\frac{2.303}{t_1}\) log \(\frac{[\mathrm{R}]_0}{0.9[\mathrm{R}]_0}\) = \(\frac{2.303}{t_1}\) log \(\frac{1}{0.9}\)
∴ t₁ = \(\frac{2.303}{\log k_{298}}\) × 0.04575
∴ t₁ = \(\frac{0.1054}{\log k_{298}}\) …………… (1)
પ્રારંભમાં સાંદ્રતા [R]₀ mol L^-1, T₂ = 308 K
t સમયમાં 25 % પ્રક્રિયા પૂર્ણ થાય છે.
∴ 75 % પ્રક્રિયા પૂર્ણ થયા પછીની સાંદ્રતા = [R]₀ ના 75 %
∴ [R]_t = 0.75 [R]₀ mol L^-1

પણ t₁ = t₂
∴ \(\frac{0.1059}{k_{(298)}}=\frac{0.2878}{k_{(308)}}\)
∴ \(\frac{k_{(308)}}{k_{(298)}}=\frac{0.2878}{0.1059}\) = 2.717 …………….. (3)
E_a ની ગણતરી :

∴ E_a = 75990.0 J mol^-1
= 75.99 kJ mol^-1 ≈ 76.0 kJ mol^-1
318 K તાપમાને ત્ની ગણતરી :
log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
= log 4 × 10¹⁰ – \(\frac{75990 \mathrm{~J} \mathrm{~mol}^{-1}}{2.303 \times 8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \times 318 \mathrm{~K}}\)
= 10.6021 – 12.4803
= – 1.8782 = \(\overline{2}\).1218
∴ k = Antilog \(\overline{2}\).1218
= 1.3237 × 10^-2 s^-1
= 0.013267 s^-1 ≈ 0.013 s^-1

પ્રશ્ન 30.
એક પ્રક્રિયાનો વેગ તાપમાન 293 K થી 313K વધારતાં ચાર ગણો થાય છે. પ્રક્રિયાની સક્રિયકરણ ઊર્જા ગણો, એમ ધારીને કે તે તાપમાન સાથે બદલાતી નથી.
ઉત્તર:
T₁ = 293 K
rate = r₁
અર્થાત્ k₁ અને
E_a = (?)

T₂ = 313 K
rate = r₂ = 4r₁
k₂ = 4k₁
log\(\frac{k_2}{k_1}\) = log\(\frac{4 k_1}{k_1}\) log 4

= 52863.3 J mol^-1
= 52.863 kJ mol^-1

GSEB Class 12 Chemistry રાસાયણિક ગતિકી NCERT Exemplar Questions and Answers

બહુવિકલ્પ પ્રશ્નો (પ્રકાર-I)
નીચેના પ્રશ્નોમાં એક જ વિકલ્પ સાચો છે.

પ્રશ્ન 1.
ઉદ્દીપકની ભૂમિકા ………………… બદલવાની છે.
(A) પ્રક્રિયાની ગિબ્સ ઊર્જા
(B) પ્રક્રિયાની ઍન્થાલ્પી
(C) પ્રક્રિયાની સક્રિયકરણ ઊર્જા
(D) સંતુલન અચળાંક
જવાબ
(C) પ્રક્રિયાની સક્રિયકરણ ઊર્જા
રાસાયણિક પ્રક્રિયા ઉદ્દીપકની હાજરીમાં કરાય છે ત્યારે તે પ્રક્રિયાની સક્રિયકરણની ઊર્જામાં ફેરફાર કરે છે. સક્રિયકરણની ઊર્જામાં ઘટાડો થાય છે.

પ્રશ્ન 2.
ઉદ્દીપકની હાજરીમાં, પ્રક્રિયા દરમિયાન ઉત્સર્જાતી કે શોષાતી ઉષ્મા …………………
(A) વધે છે.
(B) ઘટે છે.
(C) બદલાતી નથી
(D) વધે કે ઘટે
જવાબ
(C) બદલાતી નથી
રાસાયણિક પ્રક્રિયા ઉદ્દીપકની હાજરીમાં કરાય તોપણ પ્રક્રિયકો તથા નીપજોની ઍન્થાલ્પી અચળ રહે છે. આથી પ્રક્રિયામાં મુક્ત થતી કે શોષાતી ઉષ્મા ઉદ્દીપકની હાજરીમાં બદલાતી નથી.

પ્રશ્ન 3.
રાસાયણિક પ્રક્રિયાની સક્રિયકરણ ઊર્જા ………………….. નક્કી કરી શકાય.
(A) પ્રમાણિત તાપમાને વેગ-અચળાંક નક્કી કરવાથી
(B) બે જુદાં-જુદાં તાપમાનોએ વેગ-અચળાંકો નક્કી કરીને
(C) અથડામણની સંભાવના નક્કી કરીને
(D) ઉદ્દીપક વાપરીને
જવાબ
(B) બે જુદાં-જુદાં તાપમાનોએ વેગ-અચળાંકો નક્કી કરીને

• પ્રક્રિયાની સક્રિયકરણ ઊર્જા (E_a), તે પ્રક્રિયાના વેગ અચળાંકની ઉપર આધાર રાખે છે.
• જો T₁ તાપમાને વેગ અચળાંક = k₁
  અને T₂ તાપમાને વેગ અચળાંક = k₂ હોય તો
  log \(\frac{k_2}{k_1}=\frac{\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\left(\frac{1}{\mathrm{~T}_1}-\frac{1}{\mathrm{~T}_2}\right)\) થાય છે.
• આથી બે ભિન્ન તાપમાન T₁ અને T₂ કૅલ્વિન વેગ અચળાંક k₁ તથા k₂ ઉપરથી સક્રિયકરણ ઊર્જા ગણવામાં આવે છે.

પ્રશ્ન 4.
નીચેની આકૃતિને ધ્યાનમાં લો અને સાચો વિકલ્પ ચિનિત કરો.

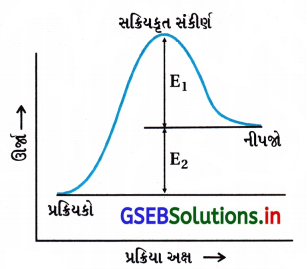
(A) પુરોગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા E₁ + E₂ છે તથા પ્રક્રિયક કરતાં નીપજ ઓછી સ્થાયી છે.
(B) પુરોગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા E₁ + E₂ છે તથા પ્રક્રિયક કરતાં નીપજ વધારે સ્થાયી છે.
(C) પુરોગામી તેમજ પ્રતિગામી બંને પ્રક્રિયાની સક્રિયકરણ ઊર્જા E₁ + E₂ છે તથા નીપજ કરતાં પ્રક્રિયક વધારે સ્થાયી છે.
(D) પ્રતિગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા E₁ છે તથા પ્રક્રિયક કરતાં નીપજ વધારે સ્થાયી છે.
જવાબ
(A) પુરોગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા E₁ + E₂ છે તથા પ્રક્રિયક કરતાં નીપજ ઓછી સ્થાયી છે.

• સક્રિયકરણ ઊર્જા = (પ્રક્રિયકોને નીપજમાં ફેરવવા માટેની જરૂરી લઘુતમ ઊર્જા)
  ∴ E_a = E₁ + E₂
• આલેખમાંથી સ્પષ્ટ છે કે-
  નીપજની સ્થિતિજ ઊર્જા > પ્રક્રિયકની સ્થિતિજ ઊર્જા
  ∴ નીપજની સ્થિરતા પ્રક્રિયકની સ્થિરતા કરતાં ઓછી છે.

પ્રશ્ન 5.
નીચે આપેલી પ્રથમ ક્રમની વાયુમય કલામાં થતી વિઘટન પ્રક્રિયા ધ્યાનમાં લો. A_(g) → B_(g) + C_(g)
Aના વિઘટન પહેલાં પ્રણાલીનું પ્રારંભિક દબાણ p_i હતું. ‘t’ સમય પછી, પ્રણાલીનું કુલ દબાણ x એકમ જેટલું વધીને P_t થયું. આ પ્રક્રિયાના વેગ અચળાંક k નું સમીકરણ છે ………………

જવાબ
(B) k = \(\frac{2.303}{t}\)log\(\frac{p_i}{2 p_i-p_t}\)

જેથી કુલ દબાણ = (p_i – x) + (x) + (x) = (p_i + x)
પણ કુલ દબાણ = P_t આપેલું છે.
p_t = (p_i + x) અને x = (p_t – p_i)
જેથી t સમય પછીથી

આમ, વિકલ્પ (B) સાચો છે.

પ્રશ્ન 6.
આર્જેનિયસ સમીકરણ મુજબ વેગ-અચળાંક k બરાબર A. \(e^{-\frac{E a}{R T}}\) . નીચેના પૈકી કયો વિકલ્પ ln k → \(\frac{1}{\mathrm{~T}}\) નો આલેખ દર્શાવે છે ?

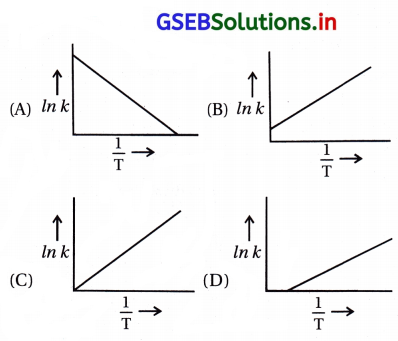
જવાબ


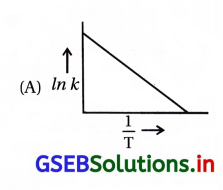
આ સૂત્ર (A) તે સીધી રેખાના સમીકરણ y = mx + c જેમાં ઢાળ = – \(\frac{\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\) અને ln k આંતરછેદ

પ્રશ્ન 7.
નીચે આપેલું આર્ટેનિયસ સમીકરણ ધ્યાનમાં લો અને સાચો પરંતુ નિખિલન વિક ચિહ્નિત કરો.
k = \(e^{-\frac{E a}{R T}}\)
(A) સક્રિયકરણ ઊર્જા વધતાં અને તાપમાન ઘટતાં વેગ- અચળાંક ઘાતાંકીય રીતે વધે છે.
(B) સક્રિયકરણ ઊર્જા વધતાં અને તાપમાન ઘટતાં વેગ- અચળાંક ઘાતાંકીય રીતે ઘટે છે.
(C) સક્રિયકરણ ઊર્જા અને તાપમાન ઘટતાં વેગ-અચળાંક ઘાતાંકીય રીતે વધે છે.
(D) સક્રિયક૨ણ ઊર્જા ઘટતાં અને તાપમાન વધતાં વેગ- અચળાંક ઘાતાંકીય રીતે વધે છે.
જવાબ
(D) સક્રિયકરણ ઊર્જા ઘટતાં અને તાપમાન વધતાં વેગ- અચળાંક ઘાતાંકીય રીતે વધે છે.
આર્જેનિયસ સમીકરણ :
k = A e^-E_a/RT
∴ k ∝ e_-1/T અને k ∝e^-E_a
∴ k ∝ T
∴ k સક્રિયકરણ ઊર્જાની ઘાતાંકમાં ઘટાડાની સાથે ઘટે છે.
∴ નું મૂલ્ય તાપમાનના વધારાની સાથે વધે છે.

પ્રશ્ન 8.
ઝિંક અને મંદ HClની પ્રક્રિયા માટે મુક્ત થતાં હાઇડ્રોજન વાયુના કદ વિરુદ્ધ સમયનો આલેખ આકૃતિમાં આપેલો છે. તેના આધારે સાચા વિક્લ્પ પર ચિહ્ન મૂકો.

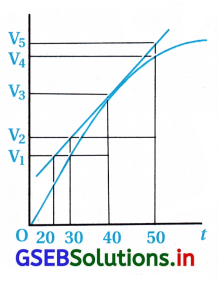
(A) 40 s સુધી સરેરાશ વેગ \(\frac{V_3-V_2}{40}\) છે.
(B) 40 s સુધી સરેરાશ વેગ \(\frac{V_3-V_2}{40-30}\) છે.
(C) 40 s સુધી સરેરાશ વેગ \(\frac{V_3}{40}\) છે.
(D) 40 s સુધી સરેરાશ વેગ \(\frac{V_3-V_1}{40-20}\) છે.
જવાબ
(C) 40 s સુધી સરેરાશ વેગ \(\frac{V_3}{40}\) છે.

• ઉપરના આલેખ પ્રમાણે –
• પ્રારંભમાં H₂ નું કદ = V₀ = 0 અને સમય = t₀ = 0
  40 s પછીથી H₂ નું કદ = V₃ અને સમય = 40 s
• H₂નો સરેરાશ વેગ = \(\frac{\Delta \mathrm{V}\left(\mathrm{H}_2\right)}{\Delta t}\)
  = \(\frac{\mathrm{V}_3-\mathrm{V}_0}{t_2-t_1}\)
  = \(\frac{V_3-0.0}{40-0.0}=\frac{V_3}{40}\)

પ્રશ્ન 9.
પ્રક્રિયાક્રમ માટે નીચેનાં વિધાનો પૈકી કયું સાચું નથી ?
(A) પ્રક્રિયાક્રમ અપૂર્ણાંક હોઈ શકે છે.
(B) પ્રક્રિયાક્રમ પ્રાયોગિક રીતે નક્કી થતી રાશિ છે.
(C) પ્રક્રિયાક્રમ હંમેશાં પ્રક્રિયાના સમતોલિત રાસાયણિક સમીકરણમાં રહેલાં પ્રક્રિયકોના તત્ત્વયોગમિતીય સહગુણાંકોના સરવાળા બરાબર હોય છે.
(D) પ્રક્રિયાક્રમ વેગનિયમના સમીકરણમાં રહેલા પ્રક્રિયકોની મોલર સાંદ્રતાના ઘાતના સરવાળા જેટલો હોય છે.
જવાબ
(C) પ્રક્રિયાક્રમ હંમેશાં પ્રક્રિયાના સમતોલિત રાસાયણિક સમીકરણમાં રહેલાં પ્રક્રિયકોના તત્ત્વયોગમિતીય સહગુણાંકોના સરવાળા બરાબર હોય છે.

• વિકલ્પ (C) ખોટો છે.
• સામાન્ય પ્રક્રિયા xA + yB → નીપજો
  પ્રક્રિયાવેગ = k [A]^x [B]^y
• તો x અને y તે A અને Bના સંદર્ભમાં પ્રક્રિયાક્રમ છે અને (x + y) તે પ્રક્રિયાનો એકંદર ક્રમ છે.
• કોઈ પણ પ્રક્રિયાના માટે વેગનિયમ સૈદ્ધાંતિક રીતે નહીં પણ પ્રાયોગિક રીતે નક્કી કરાય છે; આથી x અને y મૂલ્યો તે પ્રક્રિયકોના સહગુણાંકની ભિન્ન હોઈ શકે છે અને ફક્ત પ્રાયોગિક રીતે જ નક્કી કરાય છે.

પ્રશ્ન 10.
આકૃતિમાં આપેલો આલેખ ધ્યાનમાં લો. નીચેના વિકલ્પોમાંથી કયો 40 મી સેકન્ડે પ્રક્રિયાનો તાત્ક્ષણિક વેગ દર્શાવતો નથી ?

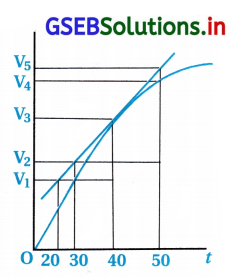
(A) \(\frac{V_5-V_2}{50-30}\)
(B) \(\frac{V_4-V_2}{50-30}\)
(C) \(\frac{V_3-V_2}{40-30}\)
(D) \(\frac{V_3-V_1}{40-20}\)
જવાબ
(B) \(\frac{V_4-V_2}{50-30}\)

• પ્રક્રિયાનો ત્વરિત વેગ r_inst = \(\frac{d[\mathrm{~V}]}{d t}\)
  40 સેકન્ડે પ્રક્રિયાનો ત્વરિત વેગ એટલે 40 સેકન્ડની નજીકના સમયગાળામાં પ્રક્રિયાનો વેગ :
• આલેખ પ્રમાણે : t
  

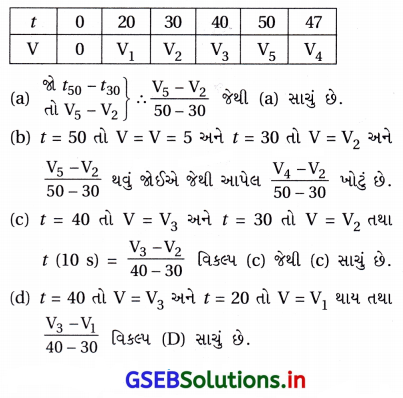
પ્રશ્ન 11.
નીચેના વિધાનોમાંથી કયું સાચું છે ?
(A) સમય જતાં પ્રક્રિયકોની સાંદ્રતા ઘટતી જતી હોવાથી પ્રક્રિયાવેગ ઘટે છે.
(B) પ્રક્રિયા દરમિયાન કોઈ પણ સમયે પ્રક્રિયાવેગ સમાન હોય છે.
(C) પ્રક્રિયાવેગ તાપમાનના ફેરફારથી સ્વતંત્ર છે.
(D) પ્રક્રિયકોની સાંદ્રતા વધે તેમ પ્રક્રિયાનો વેગ ઘટે છે.
જવાબ
(A) સમય જતાં પ્રક્રિયકોની સાંદ્રતા ઘટતી જતી હોવાથી પ્રક્રિયાવેગ ઘટે છે.
(C) ખોટું છે.
પ્રક્રિયાનો વેગ તાપમાનની ઉપર આધાર રાખે છે.

∴ પ્રક્રિયાનો વેગ ∝ Δ[R]
(i) પ્રક્રિયાનો વેગ કોઈ પણ સમયે અચળ રહેતો નથી, Δ[R] બદલાય તો બદલાય છે. (B) ખોટું છે.
(ii) જો પ્રક્રિયકોની સાંદ્રતા ઘટે તો પ્રક્રિયાવેગ પણ ઘટે છે. કારણ કે Δ[R] ઘટે છે. વિકલ્પ (A) સાચો છે.
(iii) વિકલ્પ (D) ખોટો છે, કારણ કે પ્રક્રિયકોની સાંદ્રતા વધે તો વેગ વધે છે.

પ્રશ્ન 12.
નીચે આપેલી પ્રક્રિયા માટે પ્રક્રિયાવેગની કઈ અભિવ્યક્તિ સાચી છે ?
5Br^–_(aq) + BrO^–_3(aq) + 6H⁺_(aq) → 3Br_2(aq) + 3H₂O_(l)

જવાબ
(C) \(\frac{\Delta\left[\mathrm{Br}^{-}\right]}{\Delta t}=\frac{5}{6} \frac{\Delta\left[\mathrm{H}^{+}\right]}{\Delta t}\)
આપેલી પ્રક્રિયાનું સંતુલિત સમીકરણ નીચે પ્રમાણે છે :
5Br^–_(aq) + BrO^–_3(aq) + 6H⁺_(aq) → 3Br_2(aq) + 3H₂O_(l)
જલીય માધ્યમ છે, જેથી H₂O_(l) સિવાયના દરેક સ્વિસીઝના સંદર્ભમાં પ્રક્રિયાવેગ નીચે પ્રમાણે લખાય, (જેમાં સહગુણાંકો \(\frac{1}{x}\) હોય છે) અને પ્રક્રિયકોના સંદર્ભમાં (-ve) જ્યારે નીપજોના સંદર્ભમાં (+ve) વેગ છે.

પ્રશ્ન 13.
નીચેના આલેખોમાંથી કયો ઉષ્માક્ષેપક પ્રક્રિયા દર્શાવ છે ?

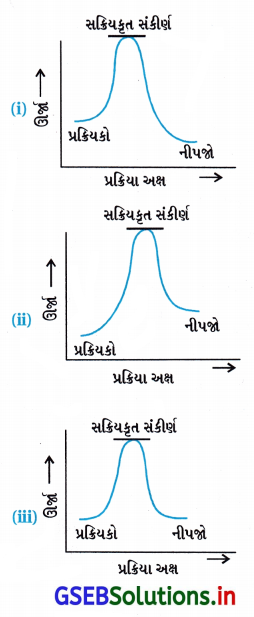
(A) ફક્ત (i)
(B) ફક્ત (ii)
(C) ફક્ત (iii)
(D) (i) અને (ii)
જવાબ
(A) ફક્ત (i)

• આકૃતિ પ્રમાણે પ્રક્રિયકોની ઊર્જા = H_R
  આકૃતિ પ્રમાણે નીપજોની ઊર્જા = H_P
  જેથી (નીપજોની ઊર્જા H_P) < (પ્રક્રિયકોની ઊર્જા H_r)
  ∴ Δ H = H_P – H_r = (-) ve
• પ્રક્રિયામાં પ્રક્રિયકમાંથી નીપજ બનતાં ઊર્જા મુક્ત થાય છે. જેથી આ આલેખ (i) ઉષ્માક્ષેપક પ્રક્રિયાનો છે.
• આલેખ (ii) ઉષ્માશોષક પ્રક્રિયાનો છે.
  આલેખ (iii) તેમાં ઉષ્મા ફેરફારો થતાં જ નથી.

પ્રશ્ન 14.
પ્રક્રિયા A + 2B → C નો વેગનિયમ નીચે મુજબ છે :
વેગ = k [A][B]
‘A’ની સાંદ્રતા અચળ રાખી, ‘B’ની સાંદ્રતા બમણી કરવામાં આવે તો વેગ-અચળાંક ………………………..
(A) તેટલો જ રહેશે.
(B) બમણો થશે.
(C) ચાર ગણો થશે.
(D) અડધો થશે.
જવાબ
(B) બમણો થશે.

• પ્રારંભમાં વેગ r₁ = k [A][B]
• જો Bની સાંદ્રતા બમણી કરીએ તો નવી સાંદ્રતા [2B]
  જેથી r₂ = k[A][2B] = 2k [A][B]
  ∴ \(\frac{r_2}{r_1}\) = 2 થાય, એટલે કે વેગ બમણો થશે.

પ્રશ્ન 15.
નીચેનાં વિધાનોમાંથી કયું રાસાયણિક પ્રક્રિયાના સંઘાત સિદ્ધાંત માટે ખોટું છે ?
(A) તેમાં પ્રક્રિયા પામતાં અણુઓ કે પરમાણુઓને સખત ગોળા તરીકે લેવામાં આવે છે તથા તેમનાં બંધારણીય લક્ષણોને અવગણવામાં આવે છે.
(B) અસરકારક સંઘાતોની સંખ્યા પ્રક્રિયાનો વેગ નક્કી કરે છે.
(C) પૂરતી થ્રેશોલ્ડ ઊર્જા (દેહલીઊર્જા) ધરાવતા પરમાણુઓ કે અણુઓ વચ્ચેના સંઘાત નીપજમાં પરિણમે છે.
(D) સંઘાતને અસરકારક (ફળદાયક) બનાવવા માટે અણુઓ પૂરતી દેહલીઊર્જા તથા યોગ્ય દિવિન્યાસ સાથે સંઘાત અનુભવવા જોઈએ.
જવાબ
(C) પૂરતી થ્રેશોલ્ડ ઊર્જા (દેહલીઊર્જા) ધરાવતા પરમાણુઓ કે અણુઓ વચ્ચેના સંઘાત નીપજમાં પરિણમે છે.
(C) ખોટું છે, કારણ કે ફક્ત પૂરતી દેહલી ઊર્જા ધરાવતા અણુઓની વચ્ચેનો સંઘાત નીપજ રચતો નથી પણ સંઘાત યોગ્ય દિશામાંથી (દિવિન્યાસવાળો) થવો આવશ્યક છે.

પ્રશ્ન 16.
એક પ્રથમ ક્રમની પ્રક્રિયા 1.26 × 10¹⁴ s માં 50% પૂર્ણ
થાય છે. તેને 100% પૂર્ણ થવા કેટલો સમય લાગશે ?
(A) 1.26 × 10¹⁵ s
(B) 2.52 × 10¹⁴ s
(C) 2.52 × 10²⁸ s
(D) અનંત સમય
જવાબ
(D) અનંત સમય

• પ્રક્રિયા 50% એટલે કે અર્ધપૂર્ણ થવાનો સમય એટલે t_1/2 જેથી
  t_1/2 = 1.26 × 10⁴s
  ∴ k = \(\frac{0.693}{t^{\frac{1}{v}}}=\frac{0.693}{1.26 \times 10^4}\)
• પ્રક્રિયા 100% પૂર્ણ થાય ત્યારે અંતિમ સાંદ્રતા = [R]_t = શૂન્ય
  
  કોઈ પણ પ્રક્રિયા t_1/2 ચોક્કસ મૂલ્ય હોય તો તેને 100% પૂર્ણ થતાં અનંત સમય થાય. તેથી વિકલ્પ (D) સાચો છે.

પ્રશ્ન 17.
સંયોજનો ‘A અને ‘B’ નીચેના રાસાયણિક સમીકરણ અનુસાર પ્રક્રિયા કરે છે.
A_(g) + 2B_(g) → 2C_(g)
બે પ્રક્રિયકોમાંથી એકની સાંદ્રતા અચળ રાખી ‘A’ અથવા ‘B’ની સાંદ્રતામાં ફેરફાર કરીને પ્રક્રિયાવેગ પ્રારંભિક સાંદ્રતાના વિધેય તરીકે માપવામાં આવ્યાં. જેમાં નીચેનાં પરિણામો મળ્યાં. આ પ્રક્રિયાના વેગ સમીકરણો માટે સાચો વિકલ્પ પસંદ કરો.

પ્રયોગ	[A]ની પ્રારંભિક સાંદ્રતા / mol L-1	[B]ની પ્રારંભિક સાંદ્રતા / mol L-1	[C] બનવાની પ્રક્રિયાનો પ્રારંભિક વેગ/mol L-1s-1
1	0.30	0.30	0.10
2	0.30	0.60	0.40
3	0.60	0.30	0.20

(A) વેગ = k [A]²[B]
(B) વેગ = k [A][B]²
(C) વેગ = k [A] [B]
(D) વેગ = [k][A]²[B]⁰
જવાબ
(B) વેગ = k [A][B]²
ધારો કે A અને B સંદર્ભમાં પ્રક્રિયાનો ક્રમ અનુક્રમે x, y છે.
વેગ : r = [A]^x[B]^y


∴ 2^x ∴ x = 1
જેથી, વેગ સમીકરણ = k [A][B]² વિકલ્પ (B) સાચો છે.

પ્રશ્ન 18.
નીચેનામાંથી કયું વિધાન ઉદ્દીપક માટે સાચું નથી ?
(A) તે પુરોગામી તથા પ્રતિગામી પ્રક્રિયાને સમાન અંશે ઉદ્દીપિત કરે છે.
(B) તે પ્રક્રિયાના ΔGમાં ફેરફાર કરે છે.
(C) તે એવો પદાર્થ છે કે જે, પ્રક્રિયાના સંતુલન અચળાંકમાં ફેરફાર કરતો નથી.
(D) તે પ્રક્રિયકો અને નીપજો વચ્ચેની સક્રિયકરણ ઊર્જા ઘટાડીને વૈકલ્પિક ક્રિયાવિધિ પૂરી પાડે છે.
જવાબ
(B) તે પ્રક્રિયાના ΔG માં ફેરફાર કરે છે.

• જ્યારે પ્રક્રિયા ઉદ્દીપકની હાજરીમાં કરવામાં આવે છે ત્યારે પ્રક્રિયાની ΔG અચળ રહે છે, બદલાતી નથી. જેથી વિધાન (B) સાચું નથી.
• વિધાન (A), (C), (D)તે ત્રણેય ઉદ્દીપકની લાક્ષણિકતાઓ છે.

પ્રશ્ન 19.
આભાસી પ્રથમ ક્રમની પ્રક્રિયાના વેગ-અચળાંકનું મૂલ્ય ……………………..
(A) અલ્પ પ્રમાણમાં રહેલાં પ્રક્રિયકોની સાંદ્રતા પર આધાર રાખે છે.
(B) અધિક પ્રમાણમાં રહેલાં પ્રક્રિયકોની સાંદ્રતા પર આધાર રાખે છે.
(C) પ્રક્રિયકોની સાંદ્રતાથી સ્વતંત્ર છે.
(D) ફક્ત તાપમાન ઉપર આધાર રાખે છે.
જવાબ
(A) અલ્પ પ્રમાણમાં રહેલાં પ્રક્રિયકોની સાંદ્રતા પર આધાર રાખે છે.

•  ઇથાઇલ એસિટેટના જળવિભાજનની પ્રક્રિયા નીચે પ્રમાણે છે :

• આ પ્રક્રિયા આભાસી પ્રથમ ક્રમની છે અને તેનો વેગ H₂O ઉપર આધાર રાખતો નથી, કારણ કે H₂Oની સાંદ્રતા લગભગ અચળ રહે છે.
  વેગ = k [CH₃COOC₂H₅]
  જ્યાં k = k₁ [H₂O] = અચળાંક
• આમ, આ આભાસી પ્રથમ ક્રમની પ્રક્રિયાનો વેગ અચળાંક ઓછો (થોડા) જથ્થાના પ્રક્રિયકની સાંદ્રતા ઉપર આધારિત છે.
• વિકલ્પ (A) સાચો છે.

પ્રશ્ન 20.
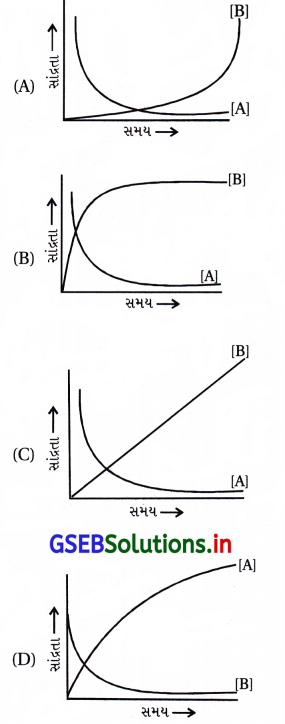
પ્રક્રિયા A B ધ્યાનમાં લો. પ્રક્રિયકો તથા નીપજો બંનેની સાંદ્રતા સમય સાથે ઘાતાંકીય રીતે બદલાય છે. નીચેના આલેખોમાંથી કઈ પ્રક્રિયકો અને નીપજોની સાંદ્રતાના સમય
સાથેના ફેરફારને સાચી રીતે દર્શાવે છે ?

જવાબ

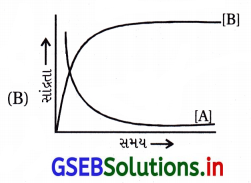
• (A) સાચી રજૂઆત નથી, કારણ કે (A)નો ઘટાડો ઝડપી જ્યારે (B)નો વધારો ધીમો છે.
• (B) સાચી રજૂઆત છે. કારણ કે તેમાં (A)નો ઘટાડો તથા (B)નો વધારો બન્ને ઝડપી હોવાથી ઘાતાંકીય છે.
• (C) સાચી રજૂઆત નથી, કારણ કે નીપજ (B)નો વધારો સુરેખ છે.
• (D) ખોટું છે, કારણ કે હંમેશાં પુરોગામી પ્રક્રિયા થાય તો પ્રક્રિયકો ઘટે અને નીપજો વધે છે પણ (D)માં (A) વધે અને (B) ઘટે જેથી (D) સાચું દર્શાવતી આકૃતિ નથી.

બહુવિકલ્પ પ્રશ્નો (પ્રકાર-II)
નીચેના પ્રશ્નોમાં બે કે વધારે વિકલ્પો સાચા હોઈ શકે છે.

પ્રશ્ન 1.
સમતોલિત રાસાયણિક સમીકરણ પરથી વેગનિયમ નક્કી કરી શકાય નહિ જો ………………………
(A) પ્રતિગામી પ્રક્રિયા સંકળાયેલી હોય.
(B) તે પ્રારંભિક પ્રક્રિયા હોય.
(C) તે પ્રારંભિક પ્રક્રિયાઓની શ્રેણી હોય.
(D) કોઈ એક પ્રક્રિયક વધુ પ્રમાણમાં હોય.
જવાબ
(A), (C), (D)
ફક્ત જો અપ્રતિવર્તીય પ્રાથમિક પ્રક્રિયા માટે જ વેગનિયમ સીધો મેળવી શકાય છે.

પ્રશ્ન 2.
પ્રારંભિક પ્રક્રિયાના સમતોલિત રાસાયણિક સમીકરણ માટે નીચેના વિધાનોમાંથી કયું લાગુ પડે છે ?
(A) આણ્વિકતા જેટલો જ ક્રમ હોય છે.
(B) આણ્વિકતા કરતાં ક્રમ ઓછો હોય છે.
(C) આણ્વિકતા કરતાં ક્રમ વધારે હોય છે.
(D) આણ્વિકતા કદાપિ શૂન્ય હોતી નથી.
જવાબ
(A), (D)
જો પ્રક્રિયાની આણ્વિકતા શૂન્ય હોય તો પ્રક્રિયકોનું નીપજમાં પરિવર્તન થાય જ નહીં, જે પ્રક્રિયા માટે અશક્ય હોવાથી પ્રક્રિયાની આણ્વિકતા શૂન્ય શક્ય નથી.

પ્રશ્ન 3.
કોઈ પણ એક આણ્વીય પ્રક્રિયામાં
(A) વેગ નિર્ણાયક તબક્કામાં માત્ર એક જ પ્રક્રિયા પામતી સ્વિસીઝ સંકળાયેલી હોય છે.
(B) સૌથી ધીમા તબક્કાના ક્રમ અને આણ્વિકતા બરાબર એક હોય છે.
(C) પ્રક્રિયાની આણ્વિકતા એક તથા ક્રમ શૂન્ય હોય છે.
(D) પ્રક્રિયાની આણ્વિકતા અને ક્રમ બંને એક હોય છે.
જવાબ
(A), (B)
પ્રક્રિયાની આણ્વીયતા = 1 છે. જેથી તેના વેગ નિર્ણાયક (ધીમા) તબક્કામાં ફક્ત એક જ સ્પિસીઝ હોય છે. પરિણામે આણ્વીયતા = ક્રમ = 1 હોય છે.

પ્રશ્ન 4.
સંકીર્ણ પ્રક્રિયા માટે …………………
(A) એકંદર પ્રક્રિયાનો ક્રમ સૌથી ધીમા તબક્કાની આણ્વિકતા જેટલો હોય છે.
(B) એકંદર પ્રક્રિયાનો ક્રમ સૌથી ધીમા તબક્કાની આણ્વિકતા કરતાં ઓછો હોય છે.
(C) એકંદર પ્રક્રિયાનો ક્રમ સૌથી ધીમા તબક્કાની આણ્વિકતા કરતાં વધારે હોય છે.
(D) સૌથી ધીમા તબક્કાની આણ્વિકતા કદાપિ શૂન્ય કે અપૂર્ણાંક હોતી નથી.
જવાબ
(A), (D)

• (A) સંકીર્ણ પ્રક્રિયાનો એકંદર પ્રક્રિયાક્રમ = સૌથી ધીમા તબક્કાની આણ્વીયતા કારણ કે (પ્રક્રિયાનો વેગ) = (સૌથી ધીમા વેગ નિર્ણાયક તબક્કાનો વેગ) જેથી (પ્રક્રિયાક્રમ) = (સૌથી ધીમા તબક્કાની આણ્વીયતા)
• (D) જો પ્રક્રિયક હોય તો જ નીપજ બની શકે છે. જેથી કદાપિ પ્રક્રિયાની આણ્વીયતા શૂન્ય કે અપૂર્ણાંક શક્ય નથી.

પ્રશ્ન 5.
ઊંચા દબાણે નીચેની પ્રક્રિયા શૂન્ય ક્રમની છે :
2NH_3(g) N_2(g) + 3H_2(g)
આ પ્રક્રિયા માટે નીચેના વિકલ્પોમાંથી કયા સાચાં છે ?
(A) પ્રક્રિયાવેગ = વેગ-અચળાંક
(B) પ્રક્રિયાવેગનો આધાર એમોનિયાની સાંદ્રતા ૫૨ છે.
(C) જ્યાં સુધી એમોનિયા સંપૂર્ણપણે અદશ્ય ના થાય (વપરાઈ ના જાય) ત્યાં સુધી એમોનિયાના વિઘટનનો દર (વેગ) અચળ રહે છે.
(D) દબાણમાં હજી વધારો કરવામાં આવે તો પ્રક્રિયાવેગ બદલાશે.
જવાબ
(A), (C), (D)

• (A) આપેલી પ્રક્રિયા માટે ઊંચા દબાણે પ્રક્રિયાનો વેગ NH₃ ઉપર આધાર રાખતો નથી.
  જેથી વેગ = k [NH₃]⁰
  ∴ વેગ = k જેથી વિકલ્પ (A) સાચો છે.
• (C) જ્યાં સુધી NH₃ હોય ત્યાં સુધી તેનું વિઘટન થયા જ કરશે અને વેગ બદલાશે નહીં.
• (D) N₂ અને H₂માંથી NH₃ બનવાની પ્રક્રિયા પ્રતિવર્તી છે, જેથી
  લ-શૅટેલિયરના સિદ્ધાંત પ્રમાણે દબાણ વધારતાં આપેલી પ્રક્રિયાની પ્રતિગામી પ્રક્રિયા થાય અને પ્રક્રિયાનો વેગ બદલાય.
• આમ, (A), (C), (D) સાચાં છે.

પ્રશ્ન 6.
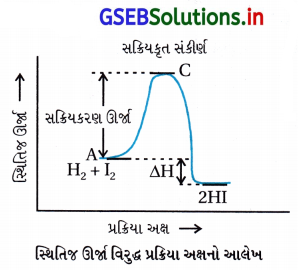
સક્રિયકૃત સંકીર્ણના વિઘટન દરમિયાન
(A) હંમેશાં ઊર્જા મુક્ત થાય છે.
(B) હંમેશાં ઊર્જાનું શોષણ થાય છે.
(C) ઊર્જામાં ફેરફાર થતો નથી.
(D) પ્રક્રિયકો બને પણ ખરા.
જવાબ
(A), (D)

• સક્રિયકૃત સંકીર્ણની ઊર્જા મહત્તમ અને પ્રક્રિયકો તથા નીપજોની ઊર્જા કરતાં વધારે હોય છે.
• જેથી સક્રિયકૃત સંકીર્ણ વિઘટન પામી ઓછી ઊર્જા ધરાવતી નીપજમાં ફેરવાય છે; સાથે પ્રક્રિયકો પણ બની શકે છે અને વિધાન (D) સાચું છે.
• ઊંચી ઊર્જાના સક્રિયકૃત સંકીર્ણ હોય છે, જે વિઘટન પામી ઓછી ઊર્જાની નીપજ રચે છે અને હંમેશાં ઊર્જા મુક્ત થાય છે. વિધાન (A) સાચું છે.
  

પ્રશ્ન 7.
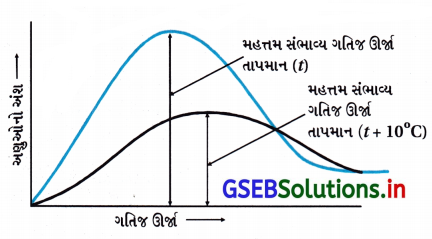
મેક્સવેલ બોલ્ટ્સમેનના ઊર્જા-વિતરણ અનુસાર …………………..
(A) ઊંચા તાપમાને સૌથી વધુ સંભાવ્ય ગતિઊર્જાવાળા અણુઓનો અંશ ઘટે છે.
(B) ઊંચા તાપમાને સૌથી વધુ સંભાવ્ય ગતિઊર્જાવાળા અણુઓનો અંશ વધે છે.
(C) ઊંચા તાપમાને સૌથી વધુ સંભાવ્ય ગતિઊર્જા વધે છે.
(D) ઊંચા તાપમાને સૌથી વધુ સંભાવ્ય ગતિઊર્જા ઘટે છે.
જવાબ
(A), (C)

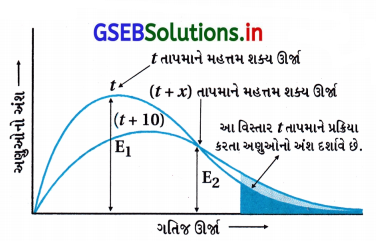
આ આલેખ પરથી સ્પષ્ટ થાય છે કે,
આ વિસ્તાર tતાપમાને પ્રક્રિયા કરતા અણુઓનો અંશ દર્શાવે છે.
(A) તાપમાનમાં વધારો કરવાથી ગતિજ ઊર્જાના અણુઓનો અંશ ઘટે છે, આલેખમાં શિખર નીચું બને છે.
(D) તાપમાનમાં વધારો કરવાથી અણુઓના અંશનું શિખર જમણી તરફ ખસે છે અને ગતિજ ઊર્જા વધે છે.

પ્રશ્ન 8.
મેક્સવેલ બોલ્ટ્સમેન ઊર્જા-વિતરણ દર્શાવતા આલેખમાં …………………..
(A) વક્રની નીચેનો વિસ્તાર તાપમાન વધતાં બદલાવો જોઈએ નહિ.
(B) વક્રની નીચેનો વિસ્તાર તાપમાન વધે તેમ વધે છે.
(C) વક્રની નીચેનો વિસ્તાર તાપમાન વધતાં ઘટે છે.
(D) તાપમાન વધતાં વક્ર પહોળો થાય છે તથા જમણી બાજુ તરફ ખસે છે.
જવાબ
(A), (D)

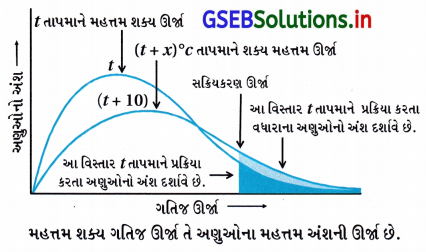
(i) આ આલેખમાં તાપમાન વધે તોપણ તેના વક્રમાંનો વિસ્તાર બદલાતો જ નથી, ભલે વક્ર બદલાય તોપણ (ii) આ આલેખના વક્રમાં સ્પષ્ટ દેખાય છે કે તાપમાન વધે તો વક્ર જમણી તરફ સ્થળાંતર પામે છે અને વક્ર પહોળો બને છે.

પ્રશ્ન 9.
નીચેનાં પૈકી કયાં વિધાનો આહેંનિયસ સમીકરણ સાથે સુસંગત છે ?
(A) તાપમાન વધે તેમ પ્રક્રિયાવેગ વધે છે.
(B) સક્રિયકરણ ઊર્જા ઘટે તેમ પ્રક્રિયાવેગ વધે છે.
(C) તાપમાન વધતાં વેગ-અચળાંક ઘાતાંકીય રીતે ઘટે છે.
(D) સક્રિયકરણ ઊર્જા ઘટે તેમ પ્રક્રિયાવેગ ઘટે છે.
જવાબ
(A), (B)

• આર્જેનિયસનું સમીકરણ, k = A\(e^{\frac{-\mathrm{E}_a}{\mathrm{RT}}}\)
  જેથી (A) k ∝ \(e^{\frac{-1}{T}}\)
  ∴ વેગ r ∝ T
• તાપમાન વધે તો પ્રક્રિયાનો વેગ વધે છે.
  (B) આર્ટેનિયસ સમીકરણમાં k ∝ e^-E_a
  જેથી k ∝ \(\frac{1}{\mathrm{E}_a}\)
• સક્રિયકરણ ઊર્જા ઘટે તો તે પ્રક્રિયાનો વેગ વધે છે.

પ્રશ્ન 10.
ખોટાં વિધાનો પર ચિહ્ન મૂકો.
(A) ઉદ્દીપક પ્રક્રિયાની ક્રિયાવિધિને વૈકલ્પિક માર્ગ પૂરો પાડે છે.
(B) ઉદ્દીપક સક્રિયકરણ ઊર્જામાં વધારો કરે છે.
(C) ઉદ્દીપક સક્રિયકરણ ઊર્જામાં ઘટાડો કરે છે.
(D) ઉદ્દીપક પ્રક્રિયાની ઍન્થાલ્પીમાં ફેરફાર કરે છે.
જવાબ
(B), (D)
ઉદ્દીપક સક્રિયકરણ ઊર્જામાં વધારો નહીં ઘટાડો કરે છે તથા ઉદ્દીપકની હાજરીમાં પ્રક્રિયાનો ઍન્થાલ્પી ફેરફાર બદલાતો નથી.

પ્રશ્ન 11.
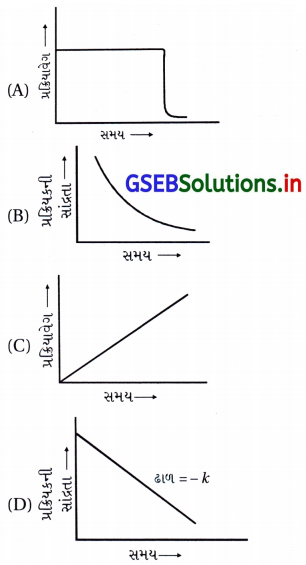
શૂન્ય ક્રમની પ્રક્રિયા માટે નીચેના આલેખોમાંથી કયો સાચો છે ?

જવાબ
(A), (D)

• શૂન્ય ક્રમની પ્રક્રિયા : R → P
  વિકલનીય વેગનિયમ : \(\frac{d[\mathrm{R}]}{d t}\) = k
• શૂન્ય ક્રમની પ્રક્રિયા માટે
  સંકલિત વેગનિયમ : kt = [R]₀ – [R]

• આ સમીકરણ (i) તે y = mx + c સ્વરૂપમાં છે, જેથી [R] → tનો આલેખ સુરેખ અને ઋણ ઢાળ ધરાવતો (D) છે.
• kt = [R]₀ – [R]
  ∴ – kt = [R] – [R]₀
  ∴ \(\frac{[\mathrm{R}]-[\mathrm{R}]_0}{\mathrm{t}}\) = – k
  ∴ \(\frac{[\mathrm{R}]-[\mathrm{R}]_0}{\mathrm{t}}\) = – kt⁰
  ∴ વેગ ∝ t⁰
• જેથી વેગ → સમયનો આલેખ વિકલ્પ (A) છે.

પ્રશ્ન 12.
પ્રથમ ક્રમની પ્રક્રિયા માટે નીચેના આલેખમાંથી કર્યો સાચો છે ?

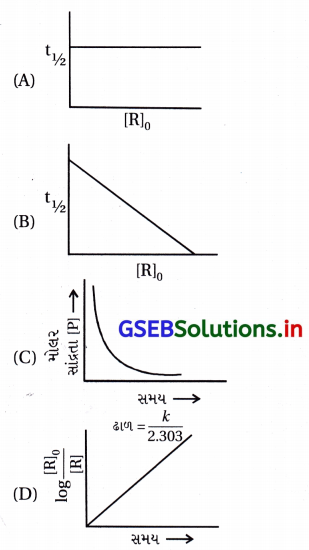
જવાબ
(A), (D)

• પ્રથમ ક્રમની પ્રક્રિયા માટે,
  ln [R] = kt + ln [R]₀

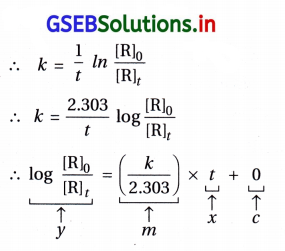
• જેથી log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]_t}\) → t નો આલેખ
• શૂન્યમાંથી પસાર થતો સીધી રેખા વિકલ્પ (D) જેવો મળે અને
  ઢાળ = \(\frac{k}{2.303}\) થાય.
• પ્રથમ ક્રમની પ્રક્રિયા માટે t_1/2 = \(\frac{0.693}{k}\)
  ∴ અર્ધઆયુષ્ય સમય પ્રક્રિયકની સાંદ્રતા [R]₀ઉપર આધાર રાખતો નથી, જેથી t_1/2 → સમયનો આલેખ વિકલ્પ (A) જેવો મળે.

ટૂંક જવાબી પ્રકારના પ્રશ્નો

પ્રશ્ન 1.
દ્વિઆણ્વીય પ્રક્રિયા ગતિકીય રીતે પ્રથમ ક્રમની કઈ શરત હેઠળ થાય તે જણાવો.
ઉત્તર:

• ઇથાઇલ એસિટેટનું જળવિભાજન દ્વિઆણ્વીય અને પ્રથમ ક્રમની પ્રક્રિયાનું ઉદાહરણ છે. જો દ્વિઆણ્વીય પ્રક્રિયામાં એક પ્રક્રિયક આધિક્યમાં હોય તો તે પ્રથમક્રમની પ્રક્રિયા હોય.

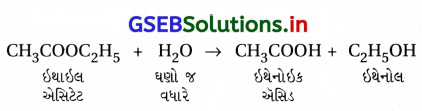
• આ પ્રક્રિયા ઢિઆણ્વીય છે પણ તેનો ક્રમ ફક્ત CH3COOCŻH5 ની સાંદ્રતાની ઉપર જ આધાર રાખે છે. [H,O] લગભગ અચળ રહે છે.

પ્રશ્ન 2.
જો પ્રક્રિયા 2A + B → C શૂન્ય ક્રમની હોય તો તેનું વેગ-સમીકરણ લખો.
ઉત્તર:

• વેગ = k [A]⁰ [B]⁰ ∴ વેગ = k
• આ પ્રક્રિયાનો વેગ A કે Bની સાંદ્રતાની ઉપર આધાર રાખતો નથી અને વેગ વેગ અચળાંક છે.

પ્રશ્ન 3.
નીચેની પ્રક્રિયાનો વેગનિયમ તમે કેવી રીતે નક્કી કરશો ?
2NO_(g) + O_2(g) → 2NO_2(g)
ઉત્તર:

• આ પ્રક્રિયાનો વેગ બે રીતે નક્કી કરી શકાય : (i) એક પ્રક્રિયકની સાંદ્રતા અચળ રાખી બીજાની સાંદ્રતા બદલીને નક્કી કરી શકાય છે. (ii) બન્ને પ્રક્રિયકોની સાંદ્રતા બદલીને પણ પ્રક્રિયાનો વેગ નક્કી કરાય છે.
• ઉદાહરણ : પ્રાયોગિક રીતે O₂ની સાંદ્રતા અચળ રાખતાં જો NOની સાંદ્રતા બમણી કરાય તો પ્રક્રિયાનો વેગ ચાર ગણો થાય છે જે વેગ ∝ [NO]²
• જેથી વેગ = k [NO]² [O₂] અને વેગનિયમની રજૂઆત નીચે પ્રમાણે થાય.
  \(-\frac{1}{2} \frac{\Delta[\mathrm{NO}]}{d t}=-\frac{\Delta\left[\mathrm{O}_2\right]}{\Delta t}=\frac{1}{2} \frac{\Delta\left[\mathrm{NO}_2\right]}{\Delta t}\)

પ્રશ્ન 4.
કયા પ્રકારની પ્રક્રિયાઓ માટે ક્રમ અને આણ્વિકતાના મૂલ્ય સમાન હોય છે ?
ઉત્તર:
પ્રાથમિક પ્રક્રિયાઓના ક્રમ અને આણ્વિકતા સમાન હોય છે.

પ્રશ્ન 5.
જો પ્રક્રિયામાં, પ્રક્રિયક Aની સાંદ્રતા ત્રણ ગણી કરવામાં આવે, તો પ્રક્રિયાવેગ સત્તાવીસ ગણો થાય છે. પ્રક્રિયાનો ક્રમ શું થશે ?
ઉત્તર:

• પ્રક્રિયાક્રમ = 3
• કોઈ પણ પ્રક્રિયા R → P અને ક્રમ = n તો વેગ r₁ = k [R]ⁿ
• હવે સાંદ્રતા ત્રણ ગણી એટલે કે 3 R કરાય તો વેગ
  r₂ = k [3R]ⁿ
  જેથી, \(\frac{r_2}{r_1}=\frac{k[3 \mathrm{R}]^n}{k[\mathrm{R}]^n}=\frac{27}{\mathrm{I}}\)
  ∴ \(\frac{{ }^{27} r_1}{r_1}\) = 27
  ∴27 = 3ⁿ
  ∴ 3 = 3ⁿ
• જેથી, n = 3

પ્રશ્ન 6.
શૂન્ય ક્રમની પ્રક્રિયાને પૂર્ણ થવા લાગતા સમયની ગણતરી કરવા માટેનું સમીકરણ તારવો.
ઉત્તર:
શૂન્યક્રમની પ્રક્રિયા માટે k = \(\frac{[\mathrm{R}]_0-[\mathrm{R}]}{t}\)
પણ પ્રક્રિયા 100% પૂર્ણ થાય ત્યારે પ્રક્રિયક Rની સાંદ્રતા = શૂન્ય થાય.
∴ [R] = 0
જેથી, k = \(\frac{[\mathrm{R}]_0-[\mathrm{R}]}{t}=\frac{[\mathrm{R}]_0}{t}\)
∴ t = \(\frac{[\mathrm{R}]_0}{k}\)

પ્રશ્ન 7.
પ્રક્રિયા A + B → નીપજો માટે, વેગનિયમ – વેગ = k [A] \([\mathrm{B}]^{\frac{3}{2}}\) છે. શું આ પ્રક્રિયા પ્રારંભિક હોઈ શકે ? સમજાવો.
ઉત્તર:

• આ પ્રક્રિયા પ્રારંભિક હોઈ શકે નહીં. આ પ્રક્રિયા સંકીર્ણ હોવી જોઈએ.
• કારણ કે પ્રારંભિક પ્રક્રિયાનો ક્રમ 1 કે 2 અને ક્યારેક જ 3 હોય છે. આ પ્રક્રિયાનો (1 +\(\frac{3}{2}\) ) = 2.5 છે. અપૂર્ણાંક છે. અપૂર્ણાંક ક્રમની પ્રક્રિયાઓ પ્રારંભિક હોતી નથી.

પ્રશ્ન 8.
એક ચોક્કસ પ્રક્રિયા માટે અણુઓનો મોટો અંશ દેહલી ઊર્જા કરતાં વધારે ઊર્જા ધરાવે છે, છતાં પણ પ્રક્રિયાવેગ ધીમો છે. શા માટે ?
ઉત્તર:
પ્રક્રિયાવેગ માટે સંઘાત સિદ્ધાંત પ્રમાણે પ્રક્રિયા થવા માટે પ્રક્રિયકના અણુઓ દેહલી ઊર્જા ઉપરનાં યોગ્ય દિસ્થાન ધરાવતા હોય તો જ નીપજ રચાય છે. જો પ્રક્રિયકના અણુ જરૂરી યોગ્ય દિફ્થાન ધરાવતા ન હોય તો પ્રક્રિયા થતી નથી, અથવા ઘણી જ ધીમી થાય છે.
વેગ = PZAB\(e^{\frac{-\mathrm{E}_{\mathrm{a}}}{\mathrm{RT}}}\), જ્યાં P = દિવિન્યાસ

પ્રશ્ન 9.
શૂન્ય ક્રમની પ્રક્રિયા માટે આણ્વિકતા શૂન્ય હોઈ શકે ? સમજાવો.
ઉત્તર:
ના, પ્રક્રિયાની આણ્વિકતા કદાપિ શૂન્ય અથવા આંશિક હોઈ શકે જ નહીં. કારણ કે અણુઓ વચ્ચે સંઘાત થાય તો જ નીપજ રચાઈ શકે છે.

પ્રશ્ન 10.
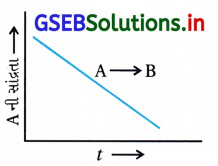
એક સામાન્ય પ્રક્રિયા A → B માં, ‘A’ ની સાંદ્રતા વિરુદ્ધ સમયનો આલેખ આકૃતિમાં આપ્યો છે. આ આલેખને આધારે નીચેના પ્રશ્નોના ઉત્તર આપો :
(i) પ્રક્રિયાનો ક્રમ કેટલો છે ?
(ii) વક્રનો ઢાળ કેટલો છે ?
(iii) વેગ-અચળાંકના એકમો શું થશે ?

ઉત્તર:
(i) પ્રક્રિયાનો ક્રમ શૂન્ય છે.
કારણ કે શૂન્ય ક્રમની પ્રક્રિયા માટે

જેથી આલેખ સીધી રેખા, ઋણ ઢાળની છે.
(ii) ઢાળ = – k
(iii) શૂન્ય ક્રમની પ્રક્રિયા જેથી વેગ અચળાંક નો એકમ mol L^-1 s^-1 છે.

પ્રશ્ન 11.
H_2(g) અને O_2(g) વચ્ચેની પ્રક્રિયા ઉચ્ચ સ્વયંસ્ફુરિત છે છતાં પણ બંને વાયુઓને એક જ પાત્રમાં ઓરડાના તાપમાને રાખી મૂકતાં પાણી બની જતું નથી. સમજાવો.
ઉત્તર:
H_2(g) અને O_2(g) વચ્ચે પ્રક્રિયા થઈને નીપજ H₂O બનવાની પ્રક્રિયાની સક્રિયકરણ ઊર્જા ઘણી વધારે છે, આથી સામાન્ય તાપમાને અપૂરતી ઊર્જા હોવાથી H₂ અને O₂ વચ્ચેના બંધ તૂટતા નથી, અને સંઘાતો થતા હોય છે, તેમ છતાં નીપજ નથી બનતી.

પ્રશ્ન 12.
શા માટે તાપમાન વધે તેમ પ્રક્રિયાવેગ વધે છે ?
ઉત્તર:

• તાપમાન વધારવાથી પ્રક્રિયકોના અણુઓની ગતિજ ઊર્જા વધે છે. તાપમાન વધતાં ગતિજ ઊર્જા સાથેનો અણુઅંશ વધવાથી, પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા પ્રાપ્ત થવાથી વધારે અણુઓ નીપજમાં ફેરવાય છે અને પ્રક્રિયાનો વેગ વધે છે.
• આર્હેનિયસ પ્રમાણે વેગ ∝ Τ
  10° તાપમાનનો વધારો kને લગભગ બમણો કરે છે.

પ્રશ્ન 13.
હવામાં ઑક્સિજન વિપુલ પ્રમાણમાં પ્રાપ્ય છે, છતાં પણ બળતણો ઓરડાના તાપમાને તેમની જાતે સળગી જતાં નથી. સમજાવો.
ઉત્તર:
બળતણના દહન માટેની જરૂરી સક્રિયકરણ ઊર્જા ઘણી વધારે છે, જે ઓરડાના તાપમાને પ્રાપ્ત નથી થતી, જેથી બળતણોનું દહન આપમેળે થઈ શકતું નથી.

પ્રશ્ન 14.
શા માટે ત્રણ કરતાં વધારે આણ્વિકતા ધરાવતી પ્રક્રિયાઓની સંભાવના ખૂબ ઓછી હોય છે ?
ઉત્તર:

• પ્રક્રિયા થવા માટે જરૂરી દેહલી સક્રિયકરણ ઊર્જા ધરાવતા અણુઓની વચ્ચે સંઘાત થવો જરૂરી છે.
• એક જ સાથે ત્રણથી વધારે અણુઓ એકબીજાની સાથે સંઘાત પામે તે વાસ્તવિક નથી, જેથી ત્રણ કરતાં વધારે આણ્વિકતાની સંભાવના અતિઅલ્પ હોય છે.

પ્રશ્ન 15.
શા માટે જેમ પ્રક્રિયા થતી જાય તેમ સામાન્યતઃ કોઈ પણ પ્રક્રિયાનો વેગ ઘટે છે ?
ઉત્તર:
કારણ કે જેમ પ્રક્રિયા નીપજ તરફ આગળ ઘસતી જાય છે તેમ તેમ પ્રક્રિયકના અણુઓની સાંદ્રતા ઘટતી જાય છે, પ્રક્રિયકોના અણુઓની વચ્ચે સંઘાતની માત્રા તથા પ્રક્રિયાનો વેગ ઘટતો જાય છે.

પ્રશ્ન 16.
પ્રક્રિયાનો વેગ પ્રક્રિયાની ઉષ્માગતિકીય સ્વયંસ્ફુરિતા માત્ર જ નક્કી કરી શકે નહિ. એક ઉદાહરણની મદદથી સમજાવો.
ઉત્તર:
ઉષ્માગતિકીય રીતે હીરાનું ચૅફાઇટમાં રૂપાંતર ઉષ્માક્ષેપક હોવાથી ઊંચી સંભાવના ધરાવે છે. આમ છતાં હીરાનું ગ્રેફાઇટમાં પરિવર્તન કરી શકાતું નથી; આ રૂપાંતર અતિ ધીમું છે. આ પ્રક્રિયાની સક્રિયકરણ ઊર્જા ઘણી જ ઊંચી છે. બીજા ઘણાં પરિબળોની ઉપર પ્રક્રિયાની સંભાવ્યતા હોય છે.

પ્રશ્ન 17.
શા માટે KMnO₄ વિ. ઓક્ઝેલિક ઍસિડના રેડોક્ષ અનુમાપનમાં, આપણે અનુમાપન શરૂ કરતાં પહેલાં ઑક્ઝેલિક એસિડના દ્રાવણને ગરમ કરીએ છીએ ?
ઉત્તર:
કા૨ણ કે સામાન્ય (ઓરડાના) તાપમાને આ અનુમાપનની પ્રક્રિયાનો વેગ ઘણો જ ધીમો હોય છે. તાપમાનમાં વધારો કરવાથી જરૂરી ગતિજ ઊર્જા (સક્રિયકરણ ઊર્જા) ધરાવતા અણુઓના અંશ વધવાથી પ્રક્રિયાવેગ વધે છે અને અનુમાપન સરળ બને છે.

પ્રશ્ન 18.
શા માટે કોઈ પણ પ્રક્રિયાની આણ્વિકતા કદાપિ શૂન્ય હોઈ શકે નહિ ?
ઉત્તર:
પ્રક્રિયાની આણ્વિકતા તે પ્રક્રિયાના પ્રાથમિક તબક્કામાં ભાગ લેતાં – સંઘાત પામતા પ્રક્રિયકના અણુઓની સંખ્યા છે. જો પ્રક્રિયકના અણુઓ ન હોય તો પ્રક્રિયા અશક્ય હોય છે, એટલે કે આણ્વિકતા શૂન્ય શક્ય નથી.

પ્રશ્ન 19.
શા માટે આણ્વિકતા ફક્ત પ્રારંભિક પ્રક્રિયાઓને જ અને પ્રક્રિયાક્રમ તે પ્રારંભિક તેમ જ સંકીર્ણ પ્રક્રિયાઓને લાગુ પડે છે ?
ઉત્તર:

• જટિલ પ્રક્રિયાઓ એક કરતાં વધારે તબક્કામાં પ્રાથમિક પ્રક્રિયાઓ થઈને થાય છે. દરેક પ્રાથમિક તબક્કામાં સંઘાત પામતા અણુઓની સંખ્યા અને આણ્વિકતા ભિન્ન હોઈ શકે છે, જેથી સમગ્ર પ્રક્રિયાની આણ્વિકતા નક્કી કરી શકાતી નથી.
• જ્યારે પ્રક્રિયાક્રમનો આધાર સૌથી ધીમા તબક્કાની ઉપર જ હોય છે. જેથી જટિલ પ્રક્રિયાનો એકંદર પ્રક્રિયાક્રમ નક્કી કરી શકાય છે.

પ્રશ્ન 20.
શા માટે આપણે સમતોલિત રાસાયણિક સમીકરણને ધ્યાનમાં લઈને પ્રક્રિયાનો ક્રમ નક્કી કરી શકીએ નહિ ?
ઉત્તર:

• સંતુલિત રાસાયણિક પ્રક્રિયામાં પ્રક્રિયકના સહગુણાંકોની સંખ્યા હંમેશાં પ્રક્રિયાના ક્રમ દર્શાવતી નથી. દા.ત.,
  (i) CHCl₃ + Cl₂ → CCl₄ + HCl
  પ્રાયોગિક વેગ સમીકરણ : k [CHCl₃]\(\left[\mathrm{Cl}_2\right]^{\frac{1}{2}}\)
  (ii) KClO₃ + 6FeSO₄ + 3H₂SO₄ → KCl + 3H₂O + 3Fe₂(SO₄)₃
• આ પ્રક્રિયા દ્વિતીય ક્રમની છે અને ઘણા તબક્કામાં પૂર્ણ થાય છે. ‘પ્રક્રિયાક્રમ ફક્ત પ્રાયોગિક રીતે જ નક્કી થાય છે.’ પણ સંતુલિત સમીકરણ ઉપર આધારિત નથી.

જોડકાં પ્રકારના પ્રશ્નો
નીચેના કેટલાક પ્રશ્નોમાં ડાબી બાજુની કૉલમનો એક વિકલ્પો જમણી બાજુના કોલમના એક અથવા એકથી વધુ વિકલ્પો સાથે સંલગ્ન હોઈ શકે છે.

પ્રશ્ન 1.
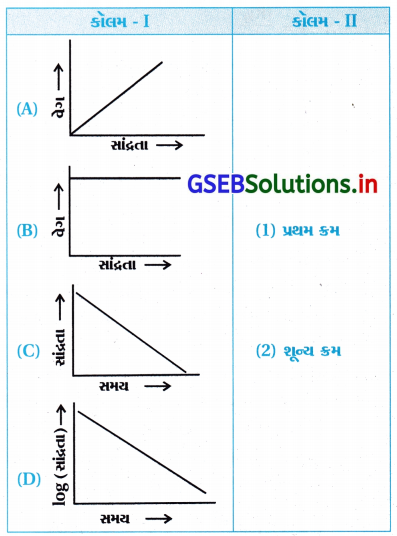
કૉલમ – Iમાં આપેલા આલેખને કૉલમ – IIમાં આપેલા પ્રક્રિયાક્રમ સાથે જોડો. સ્તંભ – Iમાંની એક કરતાં વધુ વિગત સ્તંભ – IIની એક જ વિગત સાથે જોડાઈ શકે છે.

ઉત્તર:

• (A – 1), (B – 2), (C – 2), (D – 1)
• જો પ્રક્રિયાનો ક્રમ = શૂન્ય તો તેનું સમીકરણ નીચે પ્રમાણે છે :

• જે સીધી રેખાનું સમીકરણ છે જેને નીચે પ્રમાણે લખી શકાય છે. જેથી [R] → tનો આલેખ સીધી રેખાનો આકૃતિ (C) જેવો મળે છે.
  પરિણામે, [R] – [R] = – k(t) ∴ ΔR = – k(t)
  આથી, સાંદ્રતા → સમયનો આલેખ આકૃતિ (C) જેવો મળે છે
  અને ઢાળ = – t થાય.
  શૂન્ય ક્રમની પ્રક્રિયા :
  R → નીપજનો વેગ = – \(\frac{d[\mathrm{R}]}{d t}\) = k[R]⁰ = k
• જેથી વેગ → સાંદ્રતાનો આલેખ આકૃતિ (B) જેવો સુરેખ મળે, જેમાં સાંદ્રતાની ઉપર વેગનો આધાર નથી.
• પ્રથમ ક્રમની પ્રક્રિયા :
  R → નીપજનો વેગ = – \(\frac{d[\mathrm{R}]}{d t}\) = k[R]¹
  જેથી વેગ → સાંદ્રતાનો આલેખ શૂન્યમાંથી પસાર થતો, આંતર છેદ સિવાયનો આકૃતિ (A) પ્રમાણેનો હોય છે.
• પ્રથમ ક્રમની પ્રક્રિયાના સંકલિત વેગનું સૂત્ર નીચે પ્રમાણે છે :

• જેથી log [R] → સમયનો આળેખ ઋણ ઢાળ અને આંતરછેદ [R] ધરાવતી આકૃતિ (D) જેવો મળે છે.

પ્રશ્ન 2.
કૉલમ – I અને કૉલમ-IIમાં આપેલાં વિધાનો જોડો.

કૉલમ – I	કૉલમ – II
(A) ઉદ્દીપક પ્રક્રિયાવેગમાં ફેરફાર કરે છે.	(1) અપૂર્ણાંક કે શૂન્ય હોઈ શકે નહિ.
(B) આણ્વિકતા	(2) હંમેશાં યોગ્ય દિવિન્યાસ હોતો નથી.
(C) પ્રથમ ક્રમની પ્રક્રિયાનું બીજું અર્ધઆયુષ્ય	(3) સક્રિયકરણ ઊર્જા ઘટાડીને
(D) \(e^{-\frac{\mathrm{E}_a}{\mathrm{RT}}}\)	(4) પહેલાંના જેટલું જ હોય છે.
(E) ઊર્જાની દૃષ્ટિએ તરફેણ પામતી પ્રક્રિયાઓ કેટલીક વાર ધીમી હોય છે.	(5) કુલ સંભાવના એક છે.
(F) મેક્સવેલ બોલ્ટ્સમેન વક્ર હેઠળનો વિસ્તાર અચળ છે.	(6) સક્રિયકરણ ઊર્જા જેટલી કે તેના કરતાં વધારે ઊર્જા ધરાવતા અણુઓનો અંશ દર્શાવે છે.

ઉત્તર:

કૉલમ – I	કૉલમ – II
(A) ઉદ્દીપક પ્રક્રિયાવેગમાં ફેરફાર કરે છે.	(3) સક્રિયકરણ ઊર્જા ઘટાડીને
(B) આણ્વિકતા	(1) અપૂર્ણાંક કે શૂન્ય હોઈ શકે નહિ.
(C) પ્રથમ ક્રમની પ્રક્રિયાનું બીજું અર્ધઆયુષ્ય	(4) પહેલાંના જેટલું જ હોય છે.
(D) \(e^{-\frac{\mathrm{E}_a}{\mathrm{RT}}}\)	(6) સક્રિયકરણ ઊર્જા જેટલી કે તેના કરતાં વધારે ઊર્જા ધરાવતા અણુઓનો અંશ દર્શાવે છે.
(E) ઊર્જાની દૃષ્ટિએ તરફેણ પામતી પ્રક્રિયાઓ કેટલીક વાર ધીમી હોય છે.	(2) હંમેશાં યોગ્ય દિવિન્યાસ હોતો નથી.
(F) મેક્સવેલ બોલ્ટ્સમેન વક્ર હેઠળનો વિસ્તાર અચળ છે.	(5) કુલ સંભાવના એક છે.

પ્રશ્ન 3.
કૉલમ – I અને કૉલમ – IIની વિગતો જોડો.

કૉલમ – I	કોલમ – II
(A) હીરો	(1) સમયગાળો ટૂંકો
(B) ત્વરિત વેગ	(2) સામાન્યતઃ રૂપાંતરણનો વેગ કળી (જાણી) ના શકાય.
(C) સરેરાશ વેગ	(૩) સમયગાળો લાંબો

ઉત્તર:

કૉલમ – I	કોલમ – II
(A) હીરો	(2) સામાન્યતઃ રૂપાંતરણનો વેગ કળી (જાણી) ના શકાય.
(B) ત્વરિત વેગ	(1) સમયગાળો ટૂંકો
(C) સરેરાશ વેગ	(૩) સમયગાળો લાંબો

પ્રશ્ન 4.
કૉલમ – I અને કૉલમ – IIની વિગતો જોડો.

કોલમ – I	કોલમ – II
(A) પ્રક્રિયાવેગનું ગાણિતિક સમીકરણ	(1) વેગ-અચળાંક
(B) શૂન્યક્રમની પ્રક્રિયા માટે પ્રક્રિયાવેગ બરાબર	(2) વેગનિયમ
(C) શૂન્યક્રમની પ્રક્રિયાના વેગ અચળાંકનો એકમ	(3) સૌથી ધીમા તબક્કાના ક્રમ વડે
(D) સંકીર્ણ પ્રક્રિયાનો ક્રમ નક્કી કરવામાં આવે છે.	(4) પ્રક્રિયાવેગના એકમ બરાબર

ઉત્તર:

કોલમ – I	કોલમ – II
(A) પ્રક્રિયાવેગનું ગાણિતિક સમીકરણ	(2) વેગનિયમ
(B) શૂન્યક્રમની પ્રક્રિયા માટે પ્રક્રિયાવેગ બરાબર	(1) વેગ-અચળાંક
(C) શૂન્યક્રમની પ્રક્રિયાના વેગ અચળાંકનો એકમ	(4) પ્રક્રિયાવેગના એકમ બરાબર
(D) સંકીર્ણ પ્રક્રિયાનો ક્રમ નક્કી કરવામાં આવે છે.	(3) સૌથી ધીમા તબક્કાના ક્રમ વડે

વિધાન અને કારણ પ્રકારના પ્રશ્નો

નીચેના પ્રશ્નોમાં વિધાન (A) અને ત્યાર પછી કારણ {R) આપેલું છે. પ્રશ્નોની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
(A) વિધાન (A) અને કારણ (R) બંને સાચાં છે તથા કારણ (R)એ વિધાન (A)ની સાચી સમજૂતી છે.
(B) વિધાન (A) અને કારણ (R) બંને સાચાં છે પરંતુ કારણ (R)એ વિધાન (A)ની સાચી સમજૂતી નથી.
(C) વિધાન (A) સાચું છે પરંતુ કારણ (R) ખોટું છે. (D) વિધાન (A) અને કારણ (B) બંને ખોટાં છે.
(E) વિધાન (A) ખોટું પરંતુ કારણ (R) સાચું છે.

પ્રશ્ન 1.
વિધાન (A) : પ્રક્રિયાક્રમ શૂન્ય કે અપૂર્ણાંક હોઈ શકે,
કારણ (R) : આપણે સમતોલિત રાસાયણિક સમીકરણ પરથી પ્રક્રિયાક્રમ નક્કી કરી શકીએ નહિ.
જવાબ
(B) વિધાન (A) અને કારણ (R) બંને સાચાં છે પરંતુ કારણ (R)એ વિધાન (A)ની સાચી સમજૂતી નથી.

પ્રશ્ન 2.
વિધાન (A) : પ્રક્રિયાક્રમ અને આણ્વિકતા સરખાં હોય છે.
કારણ (R) : પ્રક્રિયાક્રમ પ્રયોગિક રીતે નક્કી કરવામાં આવે છે અને આણ્વિકતા એટલે વેગનિર્ણાયક પ્રારંભિક તબક્કાના તત્ત્વયોગમિતીય સહગુણાંકોનો સરવાળો.
જવાબ
(E) વિધાન (A) ખોટું પરંતુ કારણ (B) સાચું છે.

પ્રશ્ન 3.
વિધાન (A) : ઉદ્દીપકની હાજરીમાં પ્રક્રિયાની ઍન્થાલ્પી અચળ રહે છે.
કારણ (R) : પ્રક્રિયામાં ભાગ લેતો ઉદ્દીપક, જુદા જ પ્રકારનું સક્રિયકૃત સંકીર્ણ બનાવે છે અને સક્રિયકરણ ઊર્જામાં ઘટાડો કરે છે પરંતુ પ્રક્રિયકો અને નીપજોની ઊર્જાનો તફાવત સમાન જ રહે છે.
જવાબ
(A) વિધાન (A) અને કારણ (B) બંને સાચાં છે તથા કારણ (R)એ વિધાન (A)ની સાચી સમજૂતી છે.

• પ્રક્રિયાની ઍન્થાલ્પી ΔH તે નીપજોની ઍન્થાલ્પી (H_R) અને પ્રક્રિયકોની ઍન્થાલ્પી (H_P) ના તફાવત જેટલી હોય છે. ΔH = (H_P – H_R)
• ઉદ્દીપકની હાજરીમાં પ્રક્રિયકો અને નીપોની ઊર્જા (ઍન્થાલ્પી) બદલાતી નથી. જેથી પ્રક્રિયાની ઍન્થાલ્પી બદલાતી નથી. ઉદ્દીપક અને પ્રક્રિયકો નવી સક્રિયકૃત સંકીર્ણ બનાવી પ્રક્રિયાનો માર્ગ બદલી સક્રિયકરણ ઊર્જામાં ઘટાડો કરે છે.

પ્રશ્ન 4.
વિધાન (A) : પ્રક્રિયકના અણુઓ વચ્ચે થતી બધી જ અથડામણો (સંઘાત) નીપજમાં પરિણમે છે.
કારણ (R) : ફક્ત એવી જ અથડામણો કે જેમાં અણુઓ સાચો દિવિન્યાસ તથા પૂરતી ગતિઊર્જા ધરાવતાં હોય એ જ નીપજમાં પરિણમે.
જવાબ
(E) વિધાન (A) ખોટું પરંતુ કારણ (B) સાચું છે.

• પ્રક્રિયા પામતાં અણુઓની વચ્ચે થતા દરેક સંઘાત નીપજમાં ફેરવાતા નથી જેથી વિધાન ખોટું છે.
• અસરકારક સંઘાત એટલે યોગ્ય દિાન અને પૂરતી ગતિજ ઊર્જા ધરાવતા અણુઓની વચ્ચે થતા સંઘાત હોય તે જ નીપજ બનાવી શકે છે.

પ્રશ્ન 5.
વિધાન (A) : આર્ટેનિયસ સમીકરણ વડે નક્કી કરેલા વેગ- અચળાંકો સાદા તેમ જ જટિલ અણુઓ માટે લગભગ ચોક્કસ હોય છે.
કારણ (R) : અથડામણ દરમિયાન તેમનો દિવિન્યાસ ભલે ગમે તે હોય પ્રક્રિયકના અણુઓ રાસાયણિક ફેરફાર પામે છે.
જવાબ
(C) વિધાન (A) સાચું છે પરંતુ કારણ (R) ખોટું છે.

સવિસ્તર પ્રકારના પ્રશ્નો

પ્રશ્ન 1.
ઊર્જાની દૃષ્ટિએ અસરકારક બધી જ અથડામણો (સંઘાત) રાસાયણિક ફેરફારમાં પરિણમતી નથી. એક ઉદાહરણની મદદથી સમજાવો.
ઉત્તર:

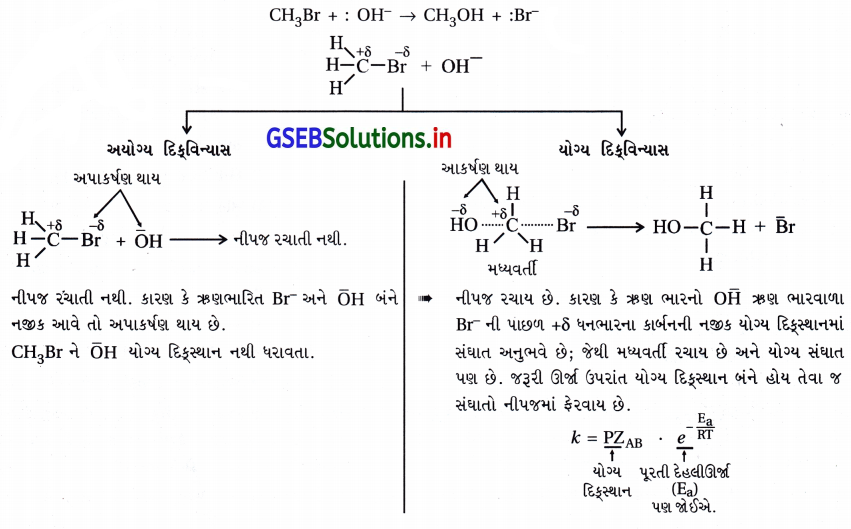
• રાસાયણિક પ્રક્રિયાથી નીપજ રચાવા માટે પ્રક્રિયા પામતા અણુઓની વચ્ચે અસરકારક સંઘાત થવા જોઈએ અને અસરકારક સંઘાત તેને જ કહેવાય કે, જેમાં અણુઓ (i) પૂરતી ગતિ ઊર્જા (દેહલી ઊર્જા) ધરાવતા હોય અને (ii) યોગ્ય દિવિન્યાસ સ્થાન ધરાવતા હોય.
• એટલે કે પૂરતી ગતિજ ઊર્જા ધરાવતો હોય પણ યોગ્ય દિસ્થાન ન ધરાવતા અણુઓ વચ્ચેનો સંઘાત નીપજમાં ફેરવાતો નથી. દા.ત., બ્રોમોમિથેનમાંથી મિથેનોલ બનાવાની પ્રક્રિયામાં મિથાઇલ બ્રોમાઇડ અને OH^– વચ્ચે જો યોગ્ય દિાનમાંથી સંઘાત થાય તો જ નીપજ રચાય છે.

પ્રશ્ન 2.
તાપમાન વધે તેમ સૌથી વધુ સંભાવ્ય ગતિજ ઊર્જા અને સક્રિયકરણ ઊર્જામાં શું થાય છે ?
ઉત્તર:

• હંમેશાં તાપમાન (t) ∝ મહત્તમ સંભાવ્ય ગતિજ ઊર્જા. તાપમાન વધારવાથી અણુઓની ગતિજ ઊર્જા વધે છે. તાપમાન વધારવાથી સૌથી વધુ સંભાવ્ય ગતિજ ઊર્જા ધરાવતો આણ્વીય અંશ વધે છે. 10° વધારવાથી K બમણો થાય છે.

• તાપમાન વધારવાથી સક્રિયકરણ ઊર્જા અને આંતરાલીય ઊર્જામાં ઘટાડો થાય છે.
  k = A · \(e^{\frac{-\mathrm{E}_{\mathrm{a}}}{\mathrm{RT}}}\)
  જેથી E_a ∝ \(\frac{1}{T}\) તાપમાન t ∝ \(\frac{1}{E_a}\)
• તાપમાનમાં વધારો કરવાથી સક્રિયકરણ ઊર્જા E_a માં ઘટાડો થાય છે.

પ્રશ્ન 3..
પ્રક્રિયામાં જ્યારે ઉદ્દીપક વાપરવામાં આવે છે ત્યારે પ્રક્રિયાની એન્થાલ્પી કેવી રીતે ફેરફાર પામતી નથી તે વર્ણવો.
ઉત્તર:

• ઉદ્દીપકની હાજરીમાં પ્રક્રિયા કરાય તો પ્રક્રિયામાંના પ્રક્રિયકની સ્થિતિજ ઊર્જા અને ઍન્થાલ્પી (H_R) તથા નીપજોની સ્થિતિજ ઊર્જા-ઍન્થાલ્પી (H_P) બદલાયા સિવાયની અચળ રહે છે.
• પ્રક્રિયાની ઍન્થાલ્પી એટલે પ્રક્રિયાનો ઍન્થાલ્પી ફેરફાર Δ_rH જે બદલાતો નથી.
  Δ_r = (H_P – H_R)
  = (નીપજોની સ્થિતિજ ઊર્જા) – (પ્રક્રિયકોની સ્થિતિજ ઊર્જા)
  = અચળ
• ΔH નું મૂલ્ય ઉદ્દીપકની હાજરીમાં બદલાતું નથી.

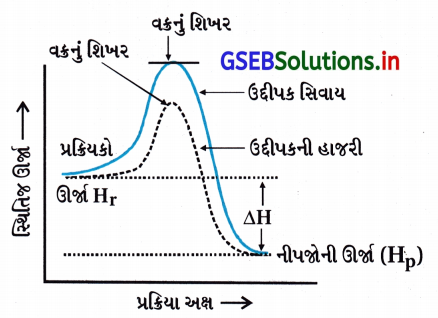
• ઉદ્દીપકની હાજરીમાં વક્રના શિખરની ઊંચાઈ ઘટે છે, સ્થિતિજ ઊર્જા અંતરાય ઘટે છે પણ પ્રક્રિયકો કે નીપજની સ્થિતિજ ઊર્જા બદલાતી નથી અને ΔH બદલાયા સિવાયની (અચળ) રહે છે.

પ્રશ્ન 4.
પ્રક્રિયાના ત્વરિત વેગ અને સરેરાશ વેગ વચ્ચેનો તફાવત સમજાવો.
ઉત્તર:

ત્વરિત વેગ	સરેરાશ વેગ
(i) ત્વરિત વેગ તે સમયના ટૂંકા ગાળાનો પ્રક્રિયાવેગ છે. – \(\frac{d[\mathrm{R}]}{d t}\) = k dR	(i) સરેરાશ વેગ તે પ્રમાણમાં પ્રક્રિયાના લાંબા સમયનો વેગ છે. – \(\frac{\Delta[\mathrm{R}]}{d t}\) = k ΔR
(ii) ત્વરિત વેગનું મૂલ્ય પ્રાથમિક પ્રક્રિયા માટે મેળવાય છે.	(ii) સરેરાશ વેગ પ્રાથમિક તેમજ જટિલ પ્રક્રિયા માટે મેળવાય છે.
(iii) ત્વરિત વેગનું મૂલ્ય આલેખથી મેળવાય છે.	(iii) સરેરાશ વેગ બે ભિન્ન સમય t1 અને t2 એ પ્રક્રિયકોની સાંદ્રતાના આધારે ગણી શકાય છે.

પ્રશ્ન 5.
આભાસી પ્રથમ ક્રમની પ્રક્રિયા એટલે શું તે એક ઉદાહરણ લઈ સમજાવો.
ઉત્તર:

• આભાસી પ્રથમ ક્રમની પ્રક્રિયા : જ્યારે ચોક્કસ તાપમાને થતી રાસાયણિક પ્રક્રિયાના બે પ્રક્રિયકોમાંથી કોઈ એક પ્રક્રિયકની સાંદ્રતા ઘણી જ વધારે હોય અને પ્રક્રિયાના અંત સુધી લગભગ બદલાતી નથી તેવી પ્રક્રિયાને આભાસી પ્રથમ ક્રમની પ્રક્રિયા કહે છે.
  ઉદાહરણ : 0.01 મોલ ઇથાઇલ એસિટેટની 10.0 મોલ પાણી સાથે જળવિભાજનની પ્રક્રિયામાં t = 0 અને t સમયે પ્રક્રિયા પૂર્ણ થઈ ઇથાઇલ એસિટેટની સાંદ્રતા = શૂન્ય બને ત્યારે
  પ્રક્રિયામાંના ભિન્ન ઘટકોની સાંદ્રતા નીચે પ્રમાણે હોય છે.

• આ પ્રક્રિયામાં પાણીની સાંદ્રતા 10 મોલમાંથી ઘટીને 9.99 મોલ થાય છે, એટલે કે લગભગ બદલાતી નથી.
  ∴ વેગ = \(\frac{-d[\mathrm{R}]}{d t}\) = k'[CH₃COOC₂H₅] [H₂O]
  અહીં,[H₂O]ને અચળ સ્વીકારવાથી k'[H₂O] નવો અચળાંક = k
  ∴ વેગ = k [CH₃COOC₂H₅]
  આવી પ્રક્રિયાને આભાસી પ્રથમ ક્રમની પ્રક્રિયા કહેવાય છે, જેમાં કોઈ એક પ્રક્રિયકની સાંદ્રતા ઘણી જ વધારે હોવાથી લગભગ બદલાતી નથી.
  પ્રેક્ટિસનો દાખલો : મિથાઇલ એસિટેટના જલીય દ્રાવણના જળવિભાજનનો અભ્યાસ મુક્ત થતાં એસિટિક એસિડના સોડિયમ હાઇડ્રોક્સાઇડ સાથેના અનુમાપન દ્વારા કરવામાં આવેલ છે. જુદા જુદા સમયે એસ્ટરની સાંદ્રતા નીચે આપેલ છે.

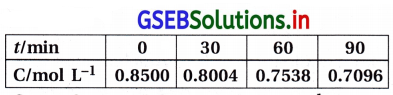
પ્રક્રિયા દરમિયાન પાણીની સાંદ્રતા (55 mol L^-1) લગભગ અચળ રહે છે. દર્શાવો કે તે આભાસી પ્રથમ ક્રમની પ્રક્રિયા છે. નીચેના સમીકરણમાં k’ નું મૂલ્ય કેટલું હશે ?
વેગ = k’ [CH₃COOCH₃] [H₂O]

• પ્રથમ ક્રમની પ્રક્રિયાના સંકલિત સ્વરૂપમાં વેગ અચળાંક
  k = \(\frac{2.303}{t}\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
  જ્યાં [R]₀ = પ્રારંભની સાંદ્રતા, t = 0 સમયે
  [R] = t સમય પછીથી સાંદ્રતા
  અહીં [R]₀ = C₀ અને [R] = C લઈએ તો,
  k = \(\frac{2.303}{t}\) log \(\frac{\mathrm{C}_0}{\mathrm{C}}\)
• જો આભાસી પ્રથમ ક્રમની પ્રક્રિયા હોય તો k = k'[H₂O]
  K₃₀ = \(\frac{2.303}{30}\) log \(\frac{0.85}{0.8004}\)
  \(\frac{2.303}{30}\) log 1.06197
  = \(\frac{2.303}{30}\) × 0.026112.004 × 10^-3 min^-1

• જેથી સરેરાશ,
  k = \(\frac{(2.004+2.002+2.006) 10^{-3} \mathrm{~min}^{-1}}{3}\)
  = 2.004 × 10^-3 min^-1
• આ પ્રક્રિયાને વેગ અચળાંક k = 2.004 × 10^-4 છે અને તે k = k’ [H₂O]નું મૂલ્ય છે. આભાસી પ્રથમ ક્રમની પ્રક્રિયાનો વેગ અચળાંક છે.
• k’નું મૂલ્ય ગણવું.
  k = k'[H₂O]
  k’ = \(\frac{k}{\left[\mathrm{H}_2 \mathrm{O}\right]}\)
  = \(\frac{2.004 \times 10^{-3}}{55.0 \mathrm{~mol} \mathrm{~L}^{-1}}\)min^-1
  = 3.6444 × 10^-5 mol^-1 L min^-1