GSEB Solutions Class 12 Maths Chapter 1 Relations and Functions Ex 1.2

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 1 Relations and Functions Ex 1.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 1 Relations and Functions Ex 1.2

Question 1.
Show that the function f: R → R, defined by f (x) = \(\frac{1}{x}\) is one-one onto, where R is the set of all non-zero real numbers. Is the result true, if the domain R is replaced by N with co-domain being same as R ?
Solution:
(i) f(x) = \(\frac{1}{x}\), If f(x₁) = f(x₂) ⇒ \(\frac{1}{x_{1}}\) = \(\frac{1}{x_{2}}\)
⇒ x₁ = x₂
Each x ∈ R, has a unique image in codomain.
⇒ f is one-one.
(ii) For each y belonging codomain, then y = \(\frac{1}{x}\) or x = \(\frac{1}{y}\), there is a unique pre-image of y.
⇒ f is onto.
(b) When domain R, is replaced by N, codomain R, remaining the same, then f : N → R,
If f(x₁) = f(x₂)
⇒ \(\frac{1}{n_{1}}\) = \(\frac{1}{n_{2}}\)
⇒ n₁ = n₂ where n₁, n₂ ∈ N.
⇒ f is one-one.
But for every real number belonging to codomain may not have a pre-image in N.
e.g. \(\frac{1}{\frac{2}{3}}\) = \(\frac{3}{2}\) ∉ N
∴ f is not onto.

Question 2.
Check the injectivity and surjectivity of the following functions:
(i) f : N → N is given by f(x) = x².
(ii) f : Z → Z is given by f(x) = x².
(iii) f : R → R is given by f(x) = x².
(iv) f : N → N is given by f(x) = x³.
(v) f : Z → Z is given by f(x) = x³.
Solution:
(i) f : N → N given by f(x) = x².
(a) f(x₁) = f(x₂) ⇒ \(x_{1}^{2}\) = \(x_{2}^{2}\) ⇒ x₁ = x₂.
∴ f is one-one, i.e., it is injective.
(b) There are some members of codomain which have no image in domain N.
e.g., 3 ∈ codomain N. But there is no pre-image in domain of f.
⇒ f is not onto, i.e., not surjective.
(ii) f : Z → Z given by f(x) = x².
(a) f(-1) = f(1) = 1 ⇒ -1 and 1 have the same image.
∴ f is not one-one, i.e., not injective.
(b) There are many elements belonging to codomain have no pre-image in its domain Z.
e.g. 3 ∈ codomain Z but \(\sqrt{3}\) ∉ domain Z of f
∴ f is not onto, i.e., not surjective.
(iii) f : R → R given by f(x) = x².
(a) f is not one-one since f(- 1) = f(1) = 1
-1 and 1 have the same image, i.e., f is not injective.
(b) – 2 ∈ codomain R of f, but \(\sqrt{-2}\) does not belong to domain R of f.
⇒ f is not onto, i.e., f is not surjective.
(iv) f: N → N given by f(x) = x³,
(a) f(x₁) = f(x₂) ⇒ \(x_{1}^{3}\) = \(x_{2}^{3}\) ⇒ x₁ = x₂
i.e., every x ∈ N has a unique image in its codomain.
∴ f is one-one. It is injective.
(b) There are many members or codomain of f which have no pre-image in its domain.
e.g., 2, 3 etc. These members of codomain have no pre-image in its domain.
∴ f is not onto, i.e., f is not surjective.
(v) f : Z → Z given by f(x) = x³.
(a) Here, also f(x₁) = f(x₂) ⇒ \(x_{1}^{3}\) = \(x_{2}^{3}\) ⇒ x₁ = x₂
∴ f is one-one, i.e., it is injective.
(b) Many members of codomain of f do not have any pre-image in its domain.
e.g., 2 belonging to its codomain has no pre-image in its domain of Z. Therefore, f is not surjective.

Question 3.
Prove that greatest integer function f : R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Solution:
f : R → R given by f(x) = [x].
(a) f(1.2) = 1, f(1.5) = 1
⇒ f is not one-one.
(b) All the images of x ∈ R belonging to its domain have integers as the images in codomain. But no fraction proper or improper belonging to codomain of f has any pre-image in its domain.
⇒ f is not onto.
Hence, f is neither one-one nor onto.

Question 4.
Show that the Modulus Function f : R → R, given by f(x) = [x], is neither one-one nor onto, where | x | is x, if x is positive and | x | is – x, if x is negative.
Solution:
f : R → R given by f(x) = | x |.
(a) f(-1) = |-1| = 1, f(1) = |1| = 1.
⇒ – 1 and 1 have the same image.
∴ f is not one-one.
(b) No negative value belonging to codomain of f has any pre-image in its domain.
∴ f is not onto.
Hence, f is neither one-one nor onto.

Question 5.
Show that the Signum function f : R → R, given by
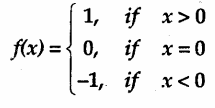is neither one-one nor onto.
-1, if x< 0
Solution:
f : R → R, given by

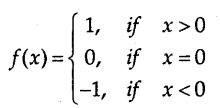
(a) f(1) = f(2) = 1
∴ 1 and 2 have the same image.
i.e. f(x₁) = f(x₂) = 1 for x > 0
⇒ x₁ ≠ x₂.
Similarly, f(x₁) = f(x₂) = —1, for x < 0,
where x₁ ≠ x₂
⇒ f is not one-one.
(b) Except – 1, 0 and 1, no other members of codomain of f has any pre-image in its domain.
f is not onto.
⇒ f is neither one-one nor onto.

Question 6.
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Solution:
A = (1, 2, 3}, B = {4, 5, 6, 7} and f = {(1, 4), (2, 5), (3, 6)}.
Every member of A has a unique image in B as shown in the figure.

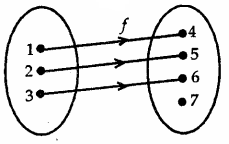
∴ f is one-one.

Question 7.
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
(i) f : R → R defined by f(x) = 3 – 4x.
(ii) f : R → R defined by f(x) = 1 + x².
Solution:
(i) f : R → R defined by f(x) = 3 – 4x.
f(x₁) = 3 – 4x₁, f(x₂) = 3 – 4x₂
(a) f(x₁) = f(x₂) ⇒ 3 – 4x₁ = 3 – 4x₂
∴ x₁ = x₂
This shows that f is one-one.

(b) f(x) = y = 3 – 4x
∴ x = \(\frac{3-y}{4}\)
For every value of y belonging to its codomain, there is a pre-image in its domain.
⇒ f is onto.
Hence, f is one-one and onto.

(ii) f : R → R given by f(x) = 1 + x²
(a) f(1) = 1 + 1 = 2, f(- 1) = 1 + 1 = 2.
∴ f(- 1) = f(1) = 2
i. e., – 1 and 1 have the same image 2.
⇒ f is not one-one.
(b) No negative number belonging to its codomain has its pre-image in its domain.
⇒ f is not onto.
Thus, f is neither one-one nor onto.

Question 8.
Let A and B be two sets. Show that f : A × B → B × A such that f(a, b) = (b, a) is bijective function.
Solution:
We have f : (A × B) → (B × A) such that f(a, b) = (b, a).
(a) ∴ f{a₁, b₁) = (b₁, a₁), f(a₂, b₂) = (b₂, a₂) and
f(a₁, b₁) = f(a₂, b₂) ⇒ (b₁, ₁) = (b₂, a₂)
⇒ b₁ = b₂ and a₁ = a₂
∴ f is onto
Thus, f is one-one and onto, ie. it is bijective.

Question 9.
Let f: N → N be defined by

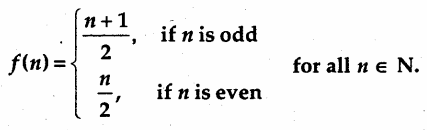
State whether the function f is bijective. Justify your answer.
Solution:
f: N → N be defined by

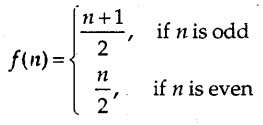
(a) f(1) = \(\frac{n+1}{2}\) = \(\frac{1+1}{2}\) = \(\frac{2}{2}\) = 1, f(2) = \(\frac{n}{2}\) = \(\frac{2}{2}\) = 1
The elements 1 and 2 belonging to domain of / have the same image in its codomain.
⇒ f is not one-one.
Therefore, it is not injective:
(b) Every member of codomain has pre-image in its domain e.g., 1 has two pre-images 1 and 2.
⇒ f is onto.
Thus, f is not one-one but it is onto. ⇒ f is not bijective.

Question 10.
Let A = R-{3} and B = R-{1}. consider the function f: A → B defined by f (x) = \(\frac{x-2}{x-3}\). Is f one-one and onto? Justify your answer.
Solution:
f : A → B, where A = R- {3}, B = R – {1}, f is defined by

or (x₁ – 2)(x₂ – 3) = (x₂ – 2)(x₁ – 3)
or x₁x₂ – 3x₁ – 2x₂ + 6 = x₁x₂ – 2x₁ – 3x₂ + 6
i.e. – 3x₁ – 2x₂ = -2x₁ – 3x₂
or -x₁ = -x₂
⇒ x₁ = x₂
∴ f is one-one.
(b) Let y = \(\frac{x-2}{x-3}\) ⇒ xy – 3y = x – 2
or x(y – 1) = 3y – 2
⇒ x = \(\frac{3 y-2}{y-1}\)
⇒ For every value of y, except y = 1, there is a pre-image
⇒ x = \(\frac{3 y-2}{y-1}\)
⇒ f is onto.
Thus, f is one-one and onto.

Question 11.
Let f: R → R be defined as f(x) = x⁴.
Choose the correct answer:
(a) f is one-one onto.
(b) f is many-one onto.
(c) f is one-one but not onto.
(d) f is neither one-one nor onto.
Solution:
f(-1) = (-1)⁴ = 1, f(1) = 1,sup>4 = 1
∴ – 1 and 1 have the same image 1.
⇒ f is not one-one.
Further – 2 in the codomain of f has no pre-image in its domain.
∴ f is not onto.
i.e., f is neither one-one nor onto.
Part (D) is the correct answer.

Question 12.
Let f: R → R be defined as f(x) = 3x.
Choose the correct answer:
(a) f is one-one onto.
(b) f is many-one onto.
(c) f is one-one but not onto.
(d) f is neither one-one nor onto.
Solution:
f : R → R is defined by f(x) = 3x.
(a) f(x₁) = 3x₁, f(x₂) = 3x₂
f(x₁) = f(x₂)
⇒ f is one-one.
(b) For every member y belonging to co-domain has pre-image x in domain of f.
Since y = 3x, ⇒ x = \(\frac{y}{3}\)
∴ f is onto.
∴ f is one-one and onto.
Part (A) is the correct answer.