Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 12 Linear Programming Ex 12.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 12 Linear Programming Ex 12.2
Question 1.
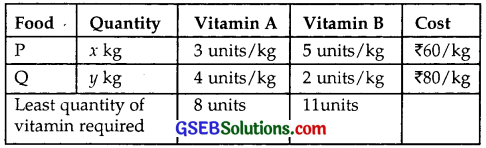
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains atleast 8 units of vitamin A and 11 units of vitamin B.
Food P costs ₹60/kg and Food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B,
while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
Solution:
Let x kg of food. P and y kg of food Q are mixed. We are given that
Quantity of vitamin A in x kg of food P and y kg of food Q
= 3x + 4 y
Quantity of vitamin A required is at least = 8 units
⇒ 3x + 4y ≥ 8
Quantity of vitamin B in x kg of foot P and y kg of food Q
= 5x + 2 y
Quantity of vitamin B required is at least = 11 units
⇒ 5x + 2y ≥ 11
Cost of x kg of food P and y kg of food Q = 60x + 80y
⇒ Objective function Z = 60x + 80y.
Constraints are 3x + 4y ≥ 8
5x + 2y ≥ 11 and x, y > 0.
(i) The line 3x + 4y = 8 passes through A(\(\frac{8}{3}\), 0) and B(0, 2).
Putting x = 0, y = 0 in 3x + 4y ≥ 8, we get 0 ≥ 8, which is not true.
⇒ The region represented by 3x + 4y ≥ 8 lies on and above AB.
(ii) The line 5x + 2y = 11 passes through C(\(\frac{11}{5}\), 0) and D(0, \(\frac{11}{2}\)).
Putting x = 0, y – 0 in 5x + 2y ≥ 11, we get 0 ≥ 11, which is not true.
⇒ Region 5x + 2y ≥ 11 lies on and above CD.
(iii) x ≥ 0 is the region on and to the right of y-axis.
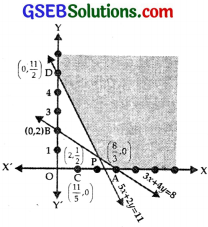
(iv) y ≥ 0 is the region on and above x-axis.
The shaded area represents the feasible region YDPAX,
where P is the point of intersection of AB and CD.
These lines are
3x + 4y = 8 ……………. (1)
5x + 2y = 11 ……………… (2)
Multiplying (2) by 2 and subtracting (1) from it, we get
7x = 22 – 8 = 14, i.e., x = 2
From (1) 4y = 8 – 3x = 8 – 6 = 2
∴ y = \(\frac{1}{2}\).
⇒ The point P is (2, \(\frac{2}{2}\)).
Now, Z = 60x + 80y
At D(0, \(\frac{11}{2}\)), Z = 80 × \(\frac{11}{2}\) = 440
At P(2, \(\frac{1}{2}\)), Z = 120 + 40 = 160
At A(\(\frac{8}{3}\), 0), Z = 60 × \(\frac{8}{3}\) + 0 = 160
Minimum value of Z = 160. But feasible region is unbounded.
∴ Consider the inequality 60x + 80y < 160
or 3x + 4y < 8
This shows that this region is below the line AD : 3x + 4y = 8.
⇒ There is no point in common between feasible region and 3x + 4y < 8.
Hence, the minimum cost Z is ₹160 at all the points lying on the line segment joining A(\(\frac{8}{3}\), 0) and P(2, \(\frac{1}{2}\)).
![]()
Question 2.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat.
Find the maximum number of cakes, which can be made from 5 kg of flour and 1 kg of fat, assuming that there is no shortage of the other ingradients, used in making the cakes.
Solution:
Let x cakes of I kind and y cakes of II kind are being made. Now, we have:

Now, objective function is Z = x + y.
Maximum quantity of flour used = 5000 g
⇒ 200x + 100y ≤ 5000
or 2x + y ≤ 50 …………… (1)
Maximum quantity of fat used = 1000 g
⇒ 25x + 50y ≤ 1000
or x + 2y ≤ 40 …………… (2)
x, y ≥ 0 ……………. (3)
(i) The line 2x + y = 50 passes through the points A(25, 0) and B(0, 50).
Putting x = 0, y = 0 in 2x + y ≤ 50, we get 0 ≤ 50, which is true.
⇒ 2x + y ≤ 50.
represents the region on and below the line AB.
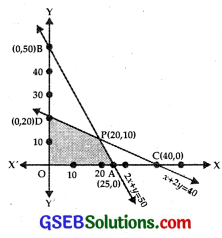
(ii) The line x + 2y – 40 passes through C(40, 0) and D(0, 20).
Putting x = 0, y = 0 in x + 2y ≤ 40,
we get 0 ≤ 40, which is true.
⇒ x + 2y ≤ 40 represents the region on and below CD.
(iii) x ≥ 0 is the region on and on the right of y-axis.
(iv) y ≥ 0 is the region on and above x-axis.
Feasible region is OAPD which is a bounded region shown by shaded area.
The lines AB 2x + y = 50 and CD x + 2y = 40 intersect at P.
∴ Solving these equations, we get x = 20 and y = 10.
The point P is (20, 10)
At A(25, 0), Z = x + y = 25 + 0 = 25
At P(20, 10), Z = 20 + 10 = 30
At (0, 20), Z = 0 + 20 = 20
At (0, 0) Z = 0
Hence, maximum value of Z is 30 at P(20, 10).
i.e., I kind of cakes 20 and II kind of cakes 10 will maximise Z.
![]()
Question 3.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of a machine time and 3 hours of craftman’s time in its making,
while a cricket bat takes 3 hours of machine time and 1 hour of craftman’s time.
In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of carftman’s time.
(i) What number of rackets and bats must be made, if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat are ₹20 and ₹10 respectively, find the maximum profit to the factory, when it works at full capacity.
Solution:
Let x tennis rackets and y cricket bats are produced in one day in the factory.
We have:
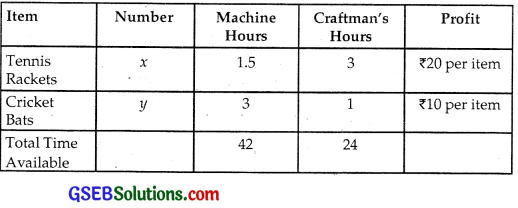
Total Machine hours = 1.5x + 3y
Maximum time available = 42 hours
⇒ 1.5x + 3y ≤ 42
or 3x + 6y ≤ 84
or x + 2y ≤ 28 …………….. (1)
Craftman’s hours = 3x + y
Maximum time available = 24
⇒ 3x + y ≤ 24 …………….. (2)
Also, x ≥ 0, y ≥ 0
(i) Z = x + y
Constraints are x + 2y ≤ 28
3x + y ≤ 24
x, y ≥ 0
Constraints are x + 2y ≤ 28
3x + y ≤ 24
x, y ≥ 0
(a) The line x + 2y = 28 passes through A(28, 0) and B(0, 14).
Putting x = 0, y = 0 in x + 2y ≤ 28,
we get 0 ≤ 28
⇒ x + 2y ≤ 28 represents the region on and below AB.
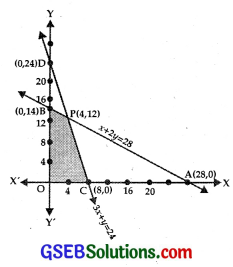
(b) The line 3x + y = 24 passes through C(8, 0) and D(0, 24).
Putting x = 0, y = 0 in 3x + y ≤ 24, we get 0 ≤ 24, which is true.
∴ 3x + y ≤ 24 represents the region on and below the line CD.
(c) x ≥ 0 represents the region on and to the right of y-axis.
(d) y ≥ 0 represents the region on and above the x-axis.
(e) The shaded area BPCO is the feasible region.
The two lines AB and CD are
x + 2y = 28 …………… (1)
3x + y = 24 ……………. (2)
Multiply equation (2) by 2 and subtract (1) from it.
We get, 5x = 48 – 28 = 20
∴ x = 4.
From (2), 12 + y = 24
⇒ y = 12.
Thus, these lines meet at P(4, 12).
(i) At B(0, 14), Z = x + y + 0 + 14 = 14
At P(4, 12), Z = 4 + 12 = 16
At C(8, 0), Z = 8 + 0 = 8
At O(0, 0), Z = 0
∴ Maximum value of Z = 16, i.e; 4 tennis rackets and 12 crkcket bats must be made so that factory works at full capacity.
(ii) Profit function is Z = 20x + 10y
At B(0, 14), Z = 0 + 10 × 14 = 140
At P(4, 12), Z = 20 × 4 + 10 × 12 = 80 + 120 = 200
At C(8, 0), Z = 20 × 8 + 0 = 120
At D(0, 0), Z = 0
Thus, maximum profit is ₹200, when 4 tennis rackets and 12 cricket bats are produced.
![]()
Question 4.
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts.
It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.
He earns a profit of ₹17.50 per packages on nuts and ₹7.00 per package on bolts.
How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
Solution:
Let x nuts and y bolts are produced.
We have the data as follows:
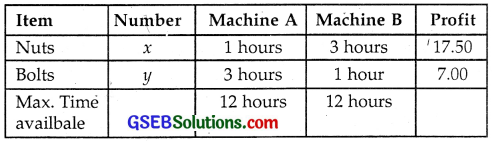
Machine A is used for x × 1 + y × 3 hours.
Maximum time available = 12 hours.
∴ x + 3y ≤ 12
Machine B is used for 3 × x + 1 × y hours
Maximum time available = 12 hours
⇒ 3x + y < 12
Profit function is Z = (17.50)x + (7.00)y
Thus, the objective function is Z = 17.5x + 7y.
Constraints are x + 3y ≤ 12, 3x + y ≤ 12 and x, y ≥ 0.
(i) The line x + 3y = 12 passes through A(12, 0) and B(0, 4).
Putting x = 0, y = 0 in x + 3y ≤ 12, we get 0 ≤ 12 is true.
⇒ x + 3y ≤ 12 lies on and below AB.
(ii) The line 3x + y = 12 passes through C(4, 0) and D(0, 12).
Putting x = 0, y = 0 in 3x + y ≤ 12, we get 0 ≤ 12, which is true.
⇒ 3x + y ≤ 12 lies on and below CD.
(iii) x ≥ 0 is the region which lies on and to the right of y-axis.
(iv) y ≥ 0 is the region which lies on and above the x-axis.
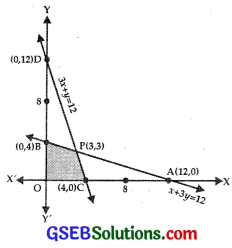
(v) The shaded area BPCO is the feasible region.
The point P is the intersection of the lines
AB : x + 3y =12 ………………… (1)
CD : 3x + y = 12 …………………..(2)
Multiplying equation (1) by 3 and subtracting (2) from it, we get
From (1), 8y = 36 – 12 = 24 ∴ y = 3
x = 12 – 3y = 12 – 9 = 3
∴ The point P is (3, 3).
Now, Z = 17.5x + 7y
At B(0, 4), Z = 0 + 7 × 4 = 28
At P(3, 3), Z = 17.5 × 3 + 7 × 3 = 52.5 + 21 = 73.5
At C(4, 0), Z = 17.5 × 4 + 0 = 70
At O(0, 0), Z = 0
Maximum profit is ₹73.50, when 3 nuts and 3 bolts packages are produced.
![]()
Question 5.
A factory manufactures two types of screws A and B, each type requires the use of two machines, an automatic and a hand operated.
It takes 4 minutes on the automatic and 6 minutes on hand operated machine to manufacture a package of screws A,
while it takes 6 minutes on automatic and 3 minutes on the hand operated machine to manufacture a package of screws B.
Each machine is available for at the most 4 hours on airy day. The manufacturer can sell a package of screws A at a profit of ₹7 and screws B at a profit of ₹10.
Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit?
Also, determine the miximum profit.
Solution:
Let the manufacturer produces x packages of screws A and y packages of screws B.
Then, time taken by x packages of screws A and y packages of screws B on automatic machine = (4x + 6y)
minutes and on hand operated machine = (6x + 3y) minutes.
As each machine is available for at the most 4 hours, i.e.,
4 × 60 = 240 minutes, so
we have:
4x + 6y ≤ 240 i.e.,
2x + 3y ≤ 120
and 6x + 3y ≤ 240, i.e.,
2x + y ≤ 80.
Profit on selling x packages of screws A and y packages of screws B is
Z = 7x + 10y
So, our problem is to find x and y such that Z = 7x + 10y is maximum subject to 2x + 3y ≤ 120, 2x + y ≤ 80, x ≥ 0 and y ≥ 0.
Plot the graphs of equations 2x + 3y = 120 and 2x + y = 80.
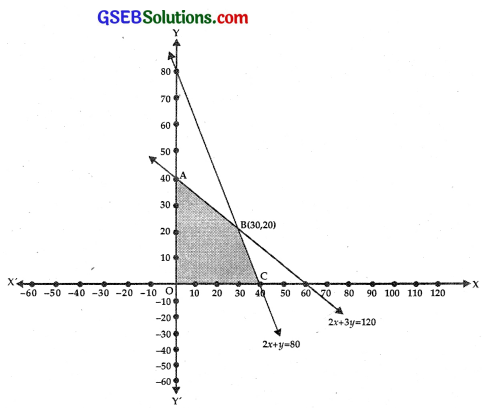
The feasible portion of the graph satisfying the inequalities 2x + 3y ≤ 120 and 2x + y ≤ 80 is OABC which is shown shaded in the figure.
Coordinates of O, A, B and C are (0, 0) (0, 4) (30, 20) and (40, 0).
We will find the values of Z at corner points O, A, B and C.
At A(0, 4), Z = 7x + 10y = 0 + 10 × 40 = 400
At B(30, 20), Z = 7 × 30 + 10 × 20 = 210 + 200 = 410
At C(40, 0), Z = 7 × 40 + 0 = 280
At O(0, 0), Z = 0
Hence, maximum profit ₹410 when 30 screws of type A and 20 screws of type B are produced.
![]()
Question 6.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer.
It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp, while if takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade.
On any day, the sprayer is available for at the most 20 hours and the grinding/ cutting machine for at the most 12 hours.
The profit from the sale of a lamp is ₹5 and that from a shade is ₹3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
Solution:
Let the manufacturer produces x pedestal lamps and y wooden shades;
then the time taken by x pedestal lamps and y wooden shades on grinding/cutting machines = (2x + y) hours and time taken by x pedestal lamps and y shades on the sprayer = (3x + 2y) hours.
Since grinding/cutting machine is available for at the most 12 hours, 2x + y ≤ 12 and sprayer is available for at the most 20 hours.
We have : 3x + 2y ≤ 20.
Profit from the sale of x lamps and y shades Z = 5x + 3y.
So, our problem is to maximise Z = 5x + 3y subject to constraints
3x + 2y ≤ 20, 2x+ y ≤ 12, x, y ≥ 0.
Plot the equation 3x + 2y, 2x + y = 12 on a graph paper.
(i) The line 2x + y = 12 passes through A(6, 0) and B(0, 12).
Putting x = 0, y = 0 in 2x + y ≤ 12, we get 0 ≤ 12, which is true.
= 2x + y ≤ 12 lies on and below AB.
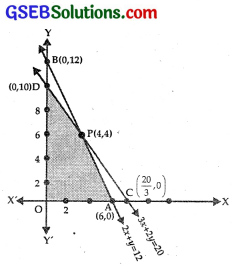
(ii) The line 3x + 2y = 20 passes through C (\(\frac{20}{3}\), 0) and D(0, 10).
Putting x = 0, y = 0 in 3x + 2y ≤ 20 lies on and below CD.
(iii) x ≥ 0 is the region on and to the right of y-axis.
(iv) y ≥ 0 is thr region on and above x-axis.
The shaded area OAPD the feasthie region, where P is the point of intersection of AB and CD.
Now, AB : 2x ÷ y = 12 ………………. (1)
CD : 3x + 2y = 20 ……………. (2)
Multiply (1) by 2 and subtract (2) from it, we get
x = 24 – 20 = 4
From(1), y = 12 – 2x = 12 – 8 = 4.
∴ Point P is (4, 4).
Now, Z = 5x + 3y
At A(6, 0), Z = 30
At P(4, 4), Z = 20 + 12 = 32
At D(0, 10), Z = 0 ÷ 30 = 30
Thus, the manufacturer should produce 4 lamps and 4 shades to get a maximum profit of ₹32.
![]()
Question 7.
A company manufactures two types of novelty souvenirs made of plywood.
Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling.
Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling.
There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profits are ₹5 each for type A and ₹6 each for type B souvenirs.
How many souvenirs of each type should the company manufacture in order to maximise the profit?
Solution:
Let the company manufactures x souvenirs of type A and y souvenirs of type B.
Then, time taken for cutting x souvenirs of type A and y souvenirs of type B = (5x + 8y) minutes.
Time taken for assembling x souvenirs of type A and y souvenirs of type B = (10x + 8y) minutes.
Since 3 hours 20 minutes, i.e., 200 minutes are available for cutting, so we should have : 5x + 8y ≤ 200.
Also, as 4 hours, i.e., 240 minutes are available for assembling, so we have 10x + 8y ≤ 240, i.e., 5x + 4y ≤ 120.
Thus, our L.P.P. is to maximise profit Z = 5x + 6y, i.e., Z = 5x + 6y subject to constraints 5x + 8y ≤ 200, 5x + 4y ≤ 120, x, y ≥ 0.
We represent the equations 5x + 8y = 200 and 5x + 4y = 120 graphically on a graph paper.
For this, we may use the following table:
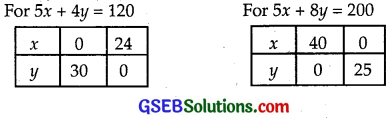
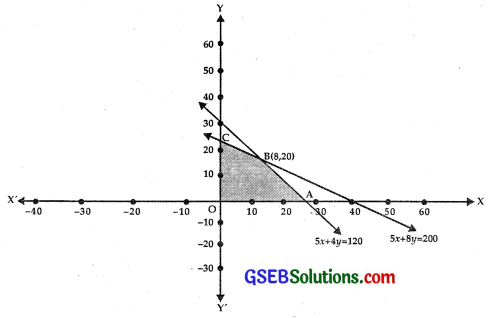
The portion of the graph satisfying the inequalities 5x + 8y ≤ 200 and 5x + 4y ≤ 120 is OABC and is shown shaded in the figure.
Coordinates of points O, A, B and C are (0, 0) (24, 0) (8, 20) and (0, 25).
The objective function is Z = 5x + 6y.
At A(24, 0), Z = 5 × 24 + 0 = 120
At B(8, 20), Z = 5 × 8 + 6 × 20 = 40 + 120 = 160
At C(0, 25), Z = 0 + 6 × 25 = 150
At D(0, 0), Z = 0
Thus, maximum prodit is ₹160, when 8 souvenirs of type A and 20 souvenirs of type B are manufactures.
![]()
Question 8.
A merchant plans to sell two types of personal computers a desk top model and a portable model that will cost ₹25000 and ₹40000 respectively.
He estimates that the total monthly demand of computers will not exceed 250 units.
Determine the number of units of each type of computers which the merchant should stock to get a maximum profit,
if he does not want to invest more than ₹70 lakh and, if his profit on the desktop model is ₹4500 and the portable is ₹5000.
Solution:
Let there be x desktop and y portable computers.
Total monthly demand of computers does not exceed 250
⇒ x + y ≤ 250.
Cost of 1 desktop computer is ₹25000 and 1 portable computer is ₹40000.
Cost of x desktop and y portable computers
= ₹(25000x + 40000y)
Maximum investment = ₹70 lakhs = ₹7000000
⇒ 25000x + 40000y ≤ 7000000
or 5x + 8y ≤ 1400
Profit on 1 desktop computer is ₹4500 and on 1 portable is ₹5000.
Total profit Z = 4500x + 5000y
∴ Objective function is to maximixe Z = 4500x + 5000y and constraints are x + y ≤ 250, 5x + 8y ≤ 1400, x, y ≥ 0.
(i) The line x + y = 250 passes through A(250, 0) and B(0, 250).
Putting x = 0, y = 0 in x + y ≤ 250, 0 ≤ 250, which is true.
⇒ x + y ≤ 250 lies on or below AB.
(ii) The line 5x + 8y = 1400 passes through C(280, 0) and D(0, 175).
Put x = 0, y = 0 in 5x + 8y ≤ 1400, 0 ≤ 1400, which is true.
⇒ 5x + 8y ≤ 1400 lies on and below CD.
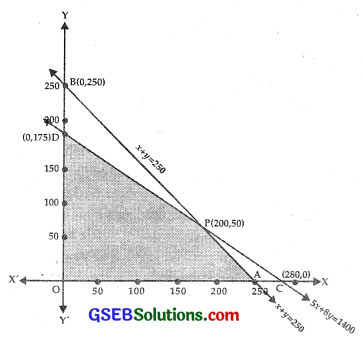
(iii) x ≥ 0 lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
The shaded area OAPD represents the feasible region, where P is the point of intersection of
5 x + 8y = 1400 ………………. (1)
x + y = 250 ………………. (2)
Multiplying (2) by 8 and subtracting (1) from it,
3x = 2000 – 1400 = 600
⇒ x = 200
∴ y = 250 – x – 250 – 200 = 50
The point P is (200, 50).
Values of Z at A, P, D, O:
At A(250, 0), Z = 4500x + 5000y
= 4500 × 250 + 0
= 1125000
At P(200, 50), Z = 4500 × 200 + 5000 × 50
= 900000 + 250000 = 1150000
At D(0, 175) Z = 0 + 5000 × 175 = 875000
⇒ Maximum profit of ₹1150000 is obtained, when he stocks 200 desktop computers and 50 portable computers.
![]()
Question 9.
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available.
Food F1 costs ₹4 per unit food and F2 costs ₹6 per unit. A unit of food F1 contains at least 3 units of vitamin A and 4 units of minerals.
One unit of food F2 contains at least 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem.
Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimum nutritional requirements.
Solution:
Let there be x units of food F1 and y units of food F2. Further the data is as follows:
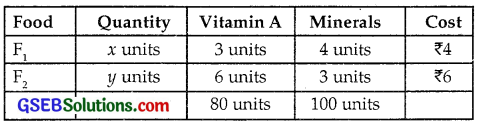
Vitamin A contained in Food F1 and F2 = 3x + 6y
Least units of vitamin A required = 80 units
⇒ 3x + 6y ≥ 80 ……………. (A)
Minerals contained in food F1 and F2 = 4x + 3y
Least quantity minerals required = 100 units.
∴ 4x + 3y ≥ 100 …………………. (B)
Therefore, L.P.P. is
To minimise Z = 4x + 6y.
Constraints are 3x + 6y ≥ 80, 4x + 3y ≥ 100 and x, y ≥ 0.
(i) The line 3x + 6y = 80 passes through A(\(\frac{80}{3}\), 0) and B(0, \(\frac{40}{3}\)).
Putting x = 0, y = 0 in 3x + 6y ≥ 80, 0 ≥ 80, which is not true.
⇒ 3x + 6y ≥ 80 lies on and above the line AB.
(ii) The line 4x + 3y = 100 passes through C (25, 0) and (0, \(\frac{100}{3}\)).
Putting x = 0, y = 0 in 4x + 3y ≥ 100, 0 ≥ 100, which is not true.
⇒ 4x + 3y ≥ 100 lies on and above CD.
(iii) x ≥ 0 lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
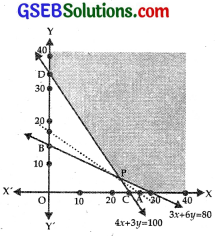
shaded area YDPAX is the feasible region .which is unbounded, where P is the point of intersection of AB and CD, i.e.,
3x + 6y = 80 ………………. (1)
and 4x + 3y – 100 ………………….. (2)
Multiplying equation (2) by 2 and subtracting (1) from it,
5x = 200 – 80 = 120 ⇒ x = 24
From (1), 72 + 6y = 80 ⇒ 6y = 8 or y = \(\frac{4}{3}\).
∴ Point P is (24, \(\frac{4}{3}\))
Value of Z = 4x + 6y :
At D(0, \(\frac{100}{3}\)), Z = 0 + 6 × \(\frac{100}{3}\) = 200
AT P(24, \(\frac{4}{3}\)), Z = 4 × 24 + 6 × \(\frac{4}{3}\) = 96 + 8 = 104
AT A(\(\frac{80}{3}\), 0), Z = 4 × \(\frac{80}{3}\) + 0 = \(\frac{320}{3}\) = 106\(\frac{2}{3}\)
Minimum value of Z is 104.
Feasible region is unbounded.
Consider the inequality 4x + 6y < 104 or 2x + 3y < 52.
The line 2x + 3y – 52 passes through (26, 0) and (0, 17\(\frac{1}{3}\)).
No point of feasible region and 4x + 6y < 104 is common to them.
The linear programming problem is:
To minimise Z = 4x + 6y, constraints are 3x + 6y = 80, from (A) and 4x + 3y = 100 from (B).
⇒ Minimum cost of diet is ₹104.
![]()
Question 10.
There are two types of fertilisers F1 and F2. F1 contains 10% nitrogen and 6% phosphoric acid and F2 consists of 5% of nitrogen and 10% of phosphoric acid.
After testing the soil conditions, a farmer finds that she needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg,
determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
Solution:
Let x kg of fertiliser F1 and y kg of fertiliser F2 is be required. We are given that:
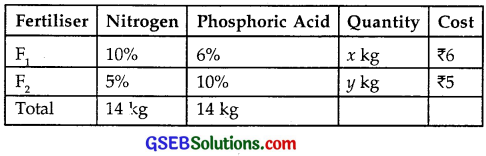
Quantity of nitrogen in F1 and F2 is
10% of x + 5% of y = \(\frac{x}{10}\) + \(\frac{y}{20}\)
Least quantity of nitrogen = 14 kg.
⇒ \(\frac{x}{10}\) + \(\frac{y}{20}\) ≥ 14 or 2x + y ≥ 280.
Quantity of phosphoric acid in fertilisers F1 and F2
= 6% of x + 10% of y
= \(\frac{6x}{100}\) + \(\frac{y}{10}\)
Least quantity of phosphoric acid = 14 kg.
⇒ \(\frac{6x}{100}\) + \(\frac{y}{10}\) ≥ 14
or 6x + 10y ≥ 1400 or 3x + 5y ≥ 700.
∴ We have to minimise the cost Z = 6x + 5y and constraints are: 2x + y ≥ 280, 3x + 5y ≥ 700, x, y ≥ 0.
(i) The line 2x + y = 280 passes through A(140, 0) and B(0, 280).
Putting x = 0, y = 0 in 2x + y ≥ 280, 0 ≥ 280, which is not true.
⇒ 2x + y ≥ 280 lies on and above AB.
(ii) The line 3x + 5y = 700 passes through C(\(\frac{700}{3}\), 0) and D(0, 140).
Putting x = 0, y = 0 in 3x + 5y ≥ 700, 0 ≥ 700, which is not true.
⇒ 3x + 5y ≥ 700 lies on and above CD.
(iii) x ≥ 0 lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above the x-axis.
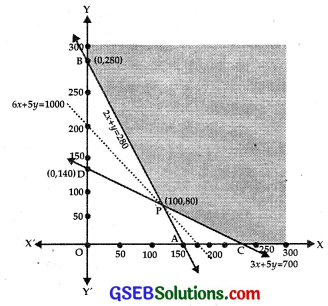
The shaded area YBPCX is the feasible region, where P 1š the point of intersection of AB and CD, i.e.,
2x + y = 280 …………….. (1)
and 3x + 5y = 700 …………….. (2)
Multiplying (1) by 5 and subtracting (2) from it, we get:
7x = 700 ⇒ x = 100.
From (1), y = 80.
∴ The point P is (100, 80).
The values of Z at B, P, C are:
At B(0, 28, 0), Z = 6x + 5y = 0 + 5 × 280 = 1400
At P(100, 80), Z = 6 × 100 + 5 × 80 = 600 ÷ 400
= 1000
At C(\(\frac{700}{3}\), 0) Z = 6 × \(\frac{700}{3}\) + 0 = 1400
∴ Z is minimum at P(100, 80), where Z = 1000.
But the feasible region is unbounded.
Consider the inequality 6x + 5y < 1000
6x + 5y = 1000 passes through (\(\frac{500}{3}\), 0) and (0, 200).
Putting x = 0, y = 0 in 6x + 5y < 1000, 0 < 1000, which is true.
∴ 6x + 5y < 1000 lies below the line 6x + 5y = 1000.
There is no point in common between feasible region and 6x + 5y < 1000.
Hence, minimum cost of Z is ₹1000, when quantities of fertiliser F1 and F2 are 100 kg and 80 kg respectively.
![]()
Question 11.
The corner points of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5)
Let Z = px + qy, where p, q > 0.
Conditions on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
(A) p = q
(B) p = 2q
(C) p = 3q
(D) q = 3p
Solution:
Maximum value of Z = px + qy occurs at (3, 4) and (0, 5)
At (3, 4), Z = px + qy = 3p + 3q
At (0, 5) Z = 0 + q.5 = 5q
Both are the maximum values.
⇒ 3p + 4q = 5q
or q = 3p.
Hence, part (D) is the correct answer.