GSEB Solutions Class 12 Maths Chapter 4 Determinants Ex 4.2

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.2

Question 1.
\(\left|\begin{array}{lll}
x & a & x+a \\
y & b & y+b \\
z & c & z+c
\end{array}\right|\) = 0
Solution:
Operating C₁ → C₁ + C₂, we get
\(\left|\begin{array}{lll}
x & a & x+a \\
y & b & y+b \\
z & c & z+c
\end{array}\right|\) = \(\left|\begin{array}{lll}
x+a & a & x+a \\
y+b & b & y+b \\
z+c & c & z+c
\end{array}\right|\) = 0,
since 1st and 3rd columns are identical.

Question 2.
\(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\) = 0
Solution:
Operating C₁ → C₁ + C₂ + C₃ we get
\(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\) = \(\left|\begin{array}{ccc}
a-b+b-c+c-a & b-c & c-a \\
b-c+c-a+a-b & c-a & a-b \\
c-a+a-b+b-c & a-b & b-c
\end{array}\right|\)
= \(\left|\begin{array}{lll}
0 & b-c & c-a \\
0 & c-a & a-b \\
0 & a-b & b-c
\end{array}\right|\) = 0,
since all elements of first column are zero.

Question 3.
\(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\) = 0
Solution:
Operating C₃ → C₃ – C₁ – 9C₂ we get:
\(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\) = \(\left|\begin{array}{lll}
2 & 7 & 0 \\
3 & 8 & 0 \\
5 & 9 & 0
\end{array}\right|\) = 0
since all the elements of 3rd column are zero.

Question 4.
\(\left|\begin{array}{lll} 1 & b c & a(b+c) \\ 1 & c a & b(c+a) \\ 1 & a b & c(a+b) \end{array}\right|\) = 0.
Solution:
Operating C₃ → C₃ + C₂, we get:
\(\left|\begin{array}{lll} 1 & b c & a(b+c) \\ 1 & c a & b(c+a) \\ 1 & a b & c(a+b) \end{array}\right|\) = \(\left|\begin{array}{lll}
1 & b c & a b+b c+c a \\
1 & c a & a b+b c+c a \\
1 & a b & a b+b c+c a
\end{array}\right|\)
Taking out ab + bc + ca common from 3rd column, we get
= (ab + bc + ca)\(\left|\begin{array}{lll}
1 & b c & 1 \\
1 & c a & 1 \\
1 & a b & 1
\end{array}\right|\) = 0.
since 1st and 3rd columns are identical.

Question 5.
\(\left|\begin{array}{ccc}
b+c & q+r & y+z \\
c+a & r+p & z+x \\
a+b & p+q & x+y
\end{array}\right|\) = 2 \(\left|\begin{array}{lll}
a & p & x \\
b & q & y \\
c & r & z
\end{array}\right|\)
Solution:

Question 6.
\(\left|\begin{array}{ccc}
0 & a & -b \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) = 0
Solution:

Question 7.
\(\left|\begin{array}{ccc}
-a^{2} & a b & a c \\
b a & -b^{2} & b c \\
a c & c b & -c^{2}
\end{array}\right|\) = 4a²b²c².
Solution:
Taking a, b, c common from I, II and III rows respectively,
we get ∆ = \(\left|\begin{array}{ccc}
-a & b & c \\
a & -b & c \\
a & b & -c
\end{array}\right|\)
Again a, b and c are taking out common from I, II and III columns respectively. we get
∴ ∆ = a²b²c²\(\left|\begin{array}{ccc}
-1 & 1 & 1 \\
1 & -1 & 1 \\
1 & 1 & -1
\end{array}\right|\)
Now operating R₁ → R₁ + R₂, we get:
∆ = a²b²c²\(\left|\begin{array}{ccc}
0 & 0 & 2 \\
1 & -1 & 1 \\
1 & 1 & -1
\end{array}\right|\) = a²b²c².2(1+1) = 4a²b²c².

Question 8.
(i) \(\left|\begin{array}{lll}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) = (a – b)(b – c)(c – a)
(ii) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\) = (a – b)(b – c)(c – a)(a + b + c)
Solution:
(i)

Taking out a – b and b – c common from R₁ and R₂ respectively,
∆ = (a-b)(b-c)\(\left|\begin{array}{ccc}
0 & 1 & a+b \\
0 & 1 & b+c \\
1 & c & c^{2}
\end{array}\right|\)
Expanding with the help of elements of first common, we get
∆ = (a-b)(b-c)\(\left|\begin{array}{ll}
1 & a+b \\
1 & b+c
\end{array}\right|\)
⇒ ∆ = (a – b)(b – c)[(b + c) – (a + b)]
⇒ ∆ = (a – b)(b – c)(c – a)

(ii)

Taking out a – b and b – c common from C₁ and C₂ respectively,
∆ = (a-b)(b-c)\(\left|\begin{array}{ccc}
0 & 0 & 1 \\
1 & 1 & c \\
a^{2}+a b+b^{2} & b^{2}+b c+c^{2} & c^{3}
\end{array}\right|\)
= (a-b)(b-c) x [(b₂ + bc + c²) – (a² + ab + b²)]
= (a – b)(b – c)[(bc – ab) + (c² – a²)]
= (a- b)(b – c)[b(c – a) + (c – a)(c + a)]
= (a- b)(b-c)(c-a)(a + b + c).

Question 9.
\(\left|\begin{array}{lll}
x & x^{2} & y z \\
y & y^{2} & z x \\
z & z^{2} & x y
\end{array}\right|\) = (x – y)(y – z)(z – x)(xy + yz + zx)
Solution:
L.H.S. ∆ = \(\left|\begin{array}{lll}
x & x^{2} & y z \\
y & y^{2} & z x \\
z & z^{2} & x y
\end{array}\right|\).
Operating R₁ → R₁ – R₂, R₂ – R₃, we get:

Question 10.
(i) \(\left|\begin{array}{ccc}
x+4 & 2 x & 2 x \\
2 x & x+4 & 2 x \\
2 x & 2 x & x+4
\end{array}\right|\) = (5x + 4)(4 – x)²
(ii) \(\left|\begin{array}{ccc}
y+k & y & y \\
y & y+k & y \\
y & y & y+k
\end{array}\right|\) = k²(3y + k)
Solution:
(i)

Expanding with the help of elements of R₁, we get
∆ = (5ac + 4)(x – 4)²[(1 – 0)]
= (5x + 4)(x – 4)2 = R.H.S.

(ii)

Question 11.

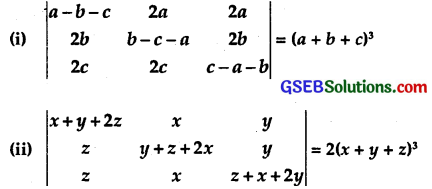
Solution:

Question 12.
\(\left|\begin{array}{lll}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\) = (1 – x³)²
Solution:
L.H.S = ∆ = \(\left|\begin{array}{lll}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\)
Operating C₁ → C₁ + C₂ + C₃, we get:

Question 13.
\(\left|\begin{array}{ccc}
1+a^{2}-b^{2} & 2 a b & -2 b \\
2 a b & 1-a^{2}+b^{2} & 2 a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\) = (1 + a² + b)³.
Solution:

Expanding with the help of elements of first row, we get
∆ = (1 + a² + b²)²[(1 – a² – b²) + 2a² + 2b²]
= (1 + a² + b²)² (1 + a² + b²)
= (1 + a² + b²)³ = R.H.S.

Question 14.
\(\left|\begin{array}{ccc}
a^{2}+1 & a b & a c \\
a b & b^{2}+1 & b c \\
c a & c b & c^{2}+1
\end{array}\right|\) = 1 + a² + b² + c².
Solution:
L.H.S = ∆ = \(\left|\begin{array}{ccc}
a^{2}+1 & a b & a c \\
a b & b^{2}+1 & b c \\
c a & c b & c^{2}+1
\end{array}\right|\)
= \(\left|\begin{array}{lll}
a^{2}+1 & a b+0 & a c+0 \\
a b+0 & b^{2}+1 & b c+0 \\
c a+0 & c b+0 & c^{2}+1
\end{array}\right|\)
This may be expressed as the sum of 8 determinants as shown below:

Question 15.
Let A be a square matrix of order 3 x 3, then | kA | is equal to
(A) k|A|
(B) k²|A|
(C) k³|A|
(D) 3k|A|
Solution:

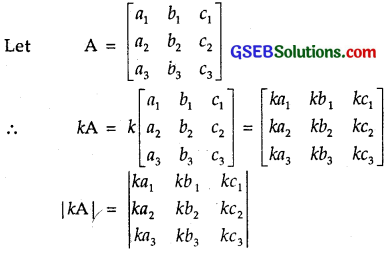
Taking out k common from each row, we get
|kA| = k³\(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|\) = k³|A|.
⇒ Part (C) is the correct answer.

Question 16.
Which of the following is correct:
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of them.
Solution:
Determinant is a number associated to a square matrix.
⇒ Part (C) is the correct.