GSEB Solutions Class 12 Maths Chapter 7 Integrals Ex 7.10

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Ex 7.10 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Ex 7.10

Evaluate the following integrals:
Question 1.
\(\int_{0}^{1}\) \(\frac{x}{x^{2}+1}\) dx
Solution:
Let I = \(\int_{0}^{1}\) \(\frac{x}{x^{2}+1}\) dx.
Put x² + 1 = t, 2x dx = dt.
When x = 1, t = 2 and when x = 0, t = 1.
∴ I = \(\int_{2}^{1}\) \(\frac{dt}{t}\)

= log 2.

Question 2.
\(\int_{0}^{\frac{\pi}{2}}\) \(\sqrt{sinϕ}\)cos⁵ϕdϕ
Solution:
Let I = \(\int_{0}^{\frac{\pi}{2}}\) \(\sqrt{sinϕ}\)cos⁵ϕdϕ
= \(\int_{0}^{\frac{\pi}{2}}\) \(\sqrt{sinϕ}\)cos⁴ϕcosϕdϕ
Put sinϕ = t so that cosϕ dϕ = dt.
When ϕ = 0, t = 0 and when ϕ = \(\frac{π}{2}\), t = 1.

Question 3.
\(\int_{0}^{1}\) sin^-1(\(\frac{2 x}{1+x^{2}}\))dx
Solution:

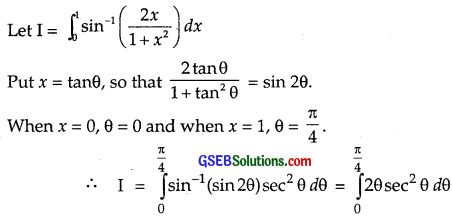
Integrating by parts, taking θ as first function,

Question 4.
\(\int_{0}^{2}\)x\(\sqrt{x+2}\) dx
Solution:
Let I = \(\int_{0}^{2}\)x\(\sqrt{x+2}\) dx
Put x + 2 = t² so that dx = 2t dt.
When x = 0, t = \(\sqrt{2}\) and when x = 2, t² = 4 ⇒ t = 2.

Question 5.
\(\int_{0}^{\frac{\pi}{2}}\) \(\frac{\sin x}{1+\cos ^{2} x}\) dx
Solution:
Let I = \(\int_{0}^{\frac{\pi}{2}}\) \(\frac{\sin x}{1+\cos ^{2} x}\) dx
Put cos x = t so that – sin x dx = dt.
When x = 0, t = cos 0 = 1 and when x = \(\frac{π}{2}\), t = cos \(\frac{π}{2}\) = 0.

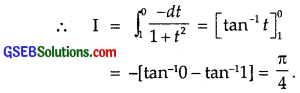
Question 6.
\(\int_{0}^{2}\) \(\frac{d x}{x+4-x^{2}}\)
Solution:

Question 7.
\(\int_{-1}^{1}\) \(\frac{d x}{x^{2}+2 x+5}\)
Solution:
Let

Question 8.
\(\int_{1}^{2}\) (\(\frac{1}{x}\) – \(\frac{1}{2 x^{2}}\) e^2x dx
Solution:

Choose the correct answers in questions 9 and 10:
Question 9.
The value of the integral \(\int_{\frac{1}{3}}^{1} \frac{\left(x-x^{3}\right)^{\frac{1}{3}}}{x^{4}}\) dx is
(A) 6
(B) 0
(C) 3
(4) 4
Solution:

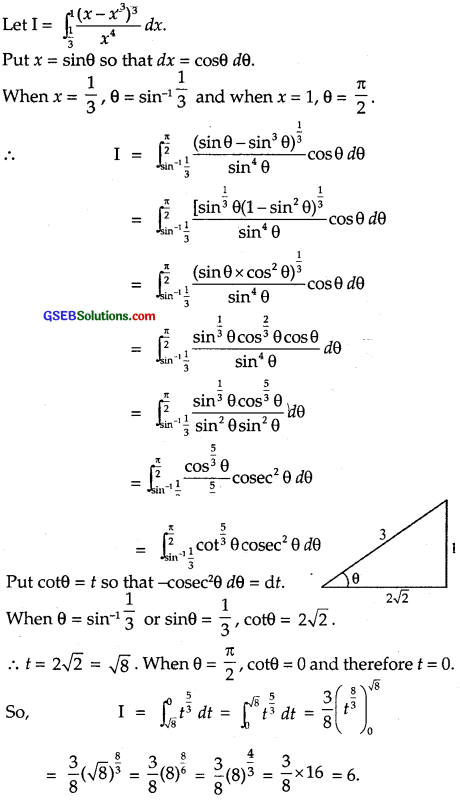
∴ Part (A) is the correct answer.

Question 10.
If f(x) = \(\int_{0}^{x}\) tsint dt, then f'(x) is
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
Solution:
R.H.S. = f(x) = \(\int_{0}^{x}\) tsint dt
Integrating, by parts taking t as first function, we get

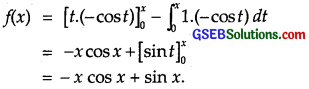
∴ f'(x) = – [1.cos x – x sin x] + cos x = x sin x.
∴ Part (B) is the correct answer.