Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Ex 7.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Ex 7.5
Integrate the following functions:
Question 1.
\(\frac{x}{(x+1)(x+2)}\)
Solution:
\(\frac{x}{(x+1)(x+2)}\) may be written as
\(\frac{x}{(x+1)(x+2)}\) = \(\frac{A}{x+1}\) + \(\frac{B}{x+2}\)
∴ x = A(x + 2) + B(x + 1)
Put x = – 1, – 1 = A(- 1 + 2) + 0 = A ∴ A = – 1.
Put x = – 2, – 2 = 0 + B(- 2 + 1) = – B ∴ B = 2.
∴ \(\frac{x}{(x+1)(x+2)}\) = – \(\frac{1}{x+1}\) + \(\frac{2}{x+2}\).
Integrating both sides, we get
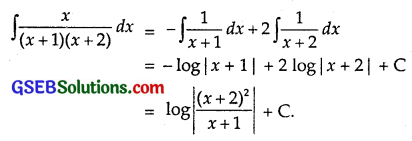
![]()
Question 2.
\(\frac{1}{x^{2}-9}\)
Solution:
Let \(\frac{1}{x^{2}-9}\) = \(\frac{1}{(x-3)(x+3)}\) = \(\frac{A}{x-3}\) + \(\frac{B}{x+3}\).
⇒ 1 = A(x + 3) + B(x – 3) ……………… (1)
Putting x = 3 in (1), we get:
1 = A(3 + 3) ⇒ A = \(\frac{1}{6}\).
Putting x = – 3 in (1), we get:
1 = B(- 3 – 3) ⇒ B = – \(\frac{1}{6}\)

Question 3.
\(\frac{3x-1}{(x-1)(x-2)(x-3)}\)
Solution:
Let \(\frac{3x-1}{(x-1)(x-2)(x-3)}\) = \(\frac{A}{x-1}\) + \(\frac{B}{x-2}\) + \(\frac{C}{x-3}\).
⇒ 3x – 1 = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x – 2) ……………….. (1)
Putting x = 1 in (1) we get:
3 – 1 = A(1 – 2)(1 – 3)
⇒ 2 = A(- 1)(- 2) ⇒ A = 1.
Putting x = 2 in (1), we get:
6 – 1 = B(2 – 1)(2 – 3)
⇒ 5 = B(1)(- 1) ⇒ B = – 5.
Putting x = 3 in (1), we get:
9 – 1 = C(3 – 1)(3 – 2)
⇒ 8 = C(2)(1) ⇒ C = 4.
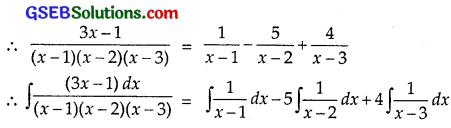
= log |x – 1| – 5 log |x – 2| + 4 log |x – 3| + C.
![]()
Question 4.
\(\frac{x}{(x-1)(x-2)(x-3)}\)
Solution:
Let \(\frac{x}{(x-1)(x-2)(x-3)}\) = \(\frac{A}{x-1}\) + \(\frac{B}{x-2}\) + \(\frac{C}{x-3}\).
⇒ x = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x – 2) …………. (1)
Putting x = 1 in (1), we get:
1 = A(1 – 2)(1 – 3)
⇒ A = \(\frac{1}{2}\)
Putting x = 2 in (1), we get:
2 = B(2 – 1)(2 – 3) ⇒ B = – 2
Putting x = 3 in (1), we get:
3 = C(3 – 1)(3 – 2) ⇒ C = \(\frac{3}{2}\).

Question 5.
\(\frac{2 x}{x^{2}+3 x+2}\)
Solution:

![]()
Question 6.
\(\frac{1-x^{2}}{x(1-2 x)}\)
Solution:
Since \(\frac{1-x^{2}}{x(1-2 x)}\) = \(\frac{1-x^{2}}{x-2 x^{2}}\) is an improper function,
therefore we convert it into a proper function. Divide 1 – x2 by x – 2x2 by long division method, we get

⇒ x – 2 = A(2x – 1) + Bx ………………. (2)
Puttting x = 0 in (2), we get:
– 2 = A(- 1) ⇒ A = 2.
Putting x = \(\frac{1}{2}\) in (2), we get:

Question 7.
\(\frac{x}{\left(x^{2}+1\right)(x-1)}\)
Solution:
\(\frac{x}{\left(x^{2}+1\right)(x-1)}\) may be written as
\(\frac{x}{\left(x^{2}+1\right)(x-1)}\) = \(\frac{A}{x-1}\) + \(\frac{B x+C}{x^{2}-1}\).
∴ x = A(x2 + 1) + (Bx + C)(x – 1)
= A(x2 + 1) + B(x2 – x) + C(x – 1)
Put x = 1, 1 = A(1 + 1) ⇒ 1 = 2A or A = \(\frac{1}{2}\)
Comparing the coefficients of x2, we get
0 = A + B
∴ B = – A = – \(\frac{1}{2}\).
Comparing the constants, we get
0 = A – C ∴ C = A = \(\frac{1}{2}\).
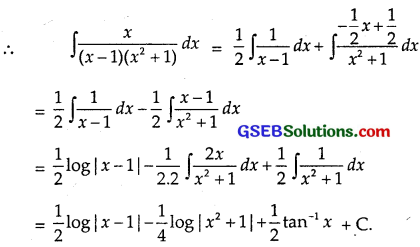
![]()
Question 8.
\(\frac{x}{(x-1)^{2}(x+2)}\)
Solution:
Let \(\frac{x}{(x-1)^{2}(x+2)}\) = \(\frac{A}{x-1}\) + \(\frac{B}{(x-1)^{2}}\) + \(\frac{C}{x+2}\).
⇒ x = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)2 …………….. (1)
Putting x = 1 in (1), we get:
1 = B(1 + 2) ⇒ B = \(\frac{1}{3}\)
Putting x = – 2 in (1), we get:
– 2 = C(- 2 – 1)2 ⇒ C = – \(\frac{-2}{9}\)
Comparing co-efficients of x2 on both sides of (1), we have:
0 = A + C ⇒ A – C = \(\frac{2}{9}\).

Question 9.
\(\frac{3 x+5}{x^{3}-x^{2}-x+1}\)
Solution:

![]()
Question 10.
\(\frac{2 x-3}{\left(x^{2}-1\right)(2 x+3)}\)
Solution:
Let \(\frac{2 x-3}{\left(x^{2}-1\right)(2 x+3)}\) = \(\frac{2x-3}{(x-1)(x+1)(2x+3)}\)
= \(\frac{A}{x-1}\) + \(\frac{B}{x+1}\) + \(\frac{C}{2x+3}\)
⇒ 2x – 3 = A(x + 1)(2x + 3) + B(x – 1)(2x + 3) + C(x – 1)(x + 1) …………….. (1)
Putting x = 1 in (1), we get
2(1) – 3 = A(1 + 1)(2 + 3)
⇒ – 1 = A(2)(5) ⇒ A = – \(\frac{1}{10}\).
Putting x = – 1 in (1), we get
– 2 – 3 = B(- 1 – 1)(- 2 + 3)
⇒ – 5 = B(- 2)(1) ⇒ B = \(\frac{5}{2}\)
Putting x = – \(\frac{3}{2}\) in (1), we get
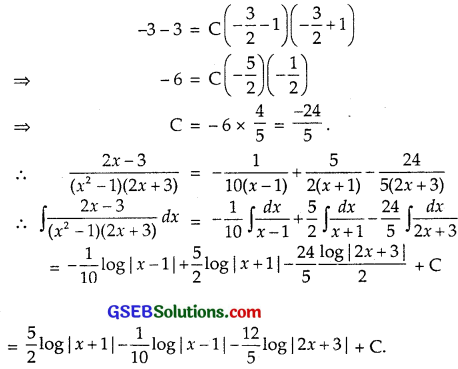
Question 11.
\(\frac{5 x}{(x+1)\left(x^{2}-4\right)}\)
Solution:
Let \(\frac{5 x}{(x+1)\left(x^{2}-4\right)}\) = \(\frac{5x}{(x+1)(x+2)(x-2)}\)
= \(\frac{A}{x+1}\) + \(\frac{B}{x+2}\) + \(\frac{C}{x-2}\)
⇒ 5x = A(x + 2)(x – 2) + B(x + 1)(x – 2) + C(x + 1)(x + 2) ………….. (1)
Putting x = – 1 in (1), we get
– 5 = A(- 1 + 2)(- 1 – 2) ⇒ A = \(\frac{5}{3}\).
Putting x = – 2 in (1), we get
– 10 = B(- 2 + 1)(- 2 – 2) ⇒ B = – \(\frac{5}{2}\)
Putting x = 2 in (1), we get
10 = C(2 + 1)(2 + 2) ⇒ C = \(\frac{5}{6}\).
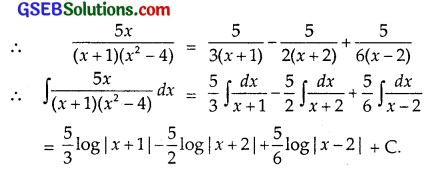
![]()
Question 12.
\(\frac{x^{3}+x+1}{x^{2}-1}\)
Solution:
Since \(\frac{x^{3}+x+1}{x^{2}-1}\) is an improper fraction, therefore we convert it into a proper fraction.
Dividing the polynomial function x3 + x + 1 by x2 – 1 by long division, we get

Putting x = – 1 in (2), we get
⇒ 2x + 1 = A(- 1 – 1) ⇒ A = \(\frac{-1}{-2}\) = \(\frac{1}{2}\).
Putting x = 1 in (2), we get
2 + 1 = B(1 + 1) ⇒ B = \(\frac{3}{2}\).
∴ \(\frac{2 x+1}{x^{2}-1}\) = \(\frac{1}{2(x+1)}\) + \(\frac{3}{2(x-1)}\) …………. (3)
From (1) and (3),
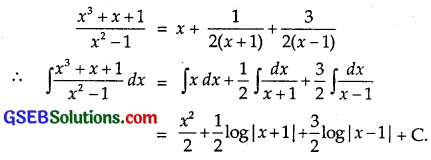
Question 13.
\(\frac{2}{(1-x)\left(1+x^{2}\right)}\)
Solution:
Let \(\frac{2 x+1}{x^{2}-1}\) = \(\frac{A}{1-x}\) + \(\frac{B x+C}{1+x^{2}}\).
⇒ 2 = A(1 + x2) + (Bx + C)(1 – x) …………… (1)
Putting x = 1 in (1), we get:
2 = A(1 + 1) ⇒ A = 1.
Comparing co-efficients of x2 and the constant terms on both sides, we get:
0 = A – B and 2 = A + C
⇒ B = A = 1 and 2 = 1 + C.
⇒ C = 1.
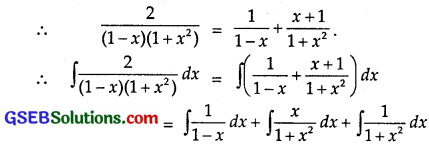
![]()
Question 14.
\(\frac{3 x-1}{(x+2)^{2}}\)
Solution:

Question 15.
\(\frac{1}{x^{4}-1}\)
Solution:
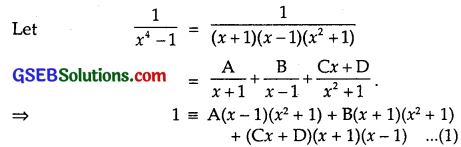
Putting x = – 1 in (1) we get:
1 = A(- 1 – 1)(1 + 1)
⇒ 1 = A(- 4) ⇒ A = – \(\frac{1}{4}\)
Putting x = 1 in (1), we get:
1 = B(1 + 1)(1 + 1)
⇒ 1 = B(2)(2) ⇒ B = \(\frac{1}{4}\).
Comparing the coefficients of x3 and constants in (1) on both sides, we get
0 = A + B + C

![]()
Question 16.
\(\frac{1}{x\left(x^{n}+1\right)}\)
Solution:
⇒ 1 = A(t + 1) + Bt …………….. (2)
Putting t = 0 in (2), we get:
1 = B(- 1) ⇒ B = – 1
∴ (1) gives:
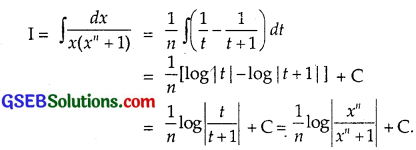
Question 17.
\(\frac{cosx}{(1-sin2x)(2-sinx)}\)
Solution:
Put sin x = t so that cos x dx = dt.
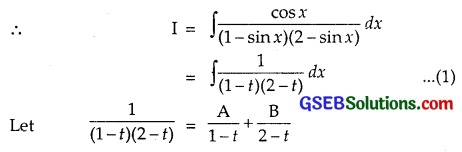
⇒ 1 = A(2 – t) + B(1 – t) …………….. (2)
Putting t = 1 in (2) we get:
1 = A(2 – 1) ⇒ A = 1.
Putting t = 2 in (2), we get:
1 = B(1 – 2) ⇒ B = – 1.
∴ (1) gives:
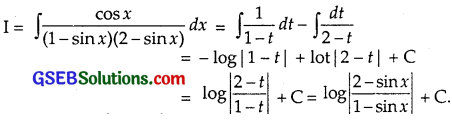
![]()
Question 18.
\(\frac{\left(x^{2}+1\right)\left(x^{2}+2\right)}{\left(x^{2}+3\right)\left(x^{2}+4\right)}\)
Solution:
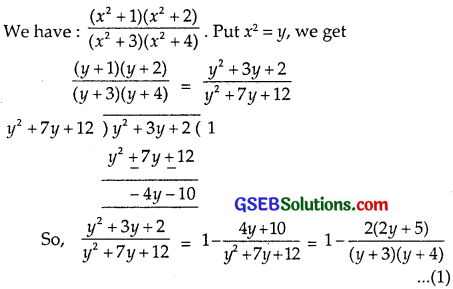
Consider partial fractions of
\(\frac{(2y+5)}{(y+3)(y+5)}\) = \(\frac{A}{y+3}\) + \(\frac{B}{y+4}\)
Put y = – 3 in (2), – 6 + 5 = A.1 ∴ A = – 1.
Put y = – 4 in (2), – 8 + 5 = B(- 4 + 3)
or – 3 = – B ∴ B = 3.
Putting these values in (1), we get

Integrated both sides

Question 19.
\(\frac{2 x}{\left(x^{2}+1\right)\left(x^{2}+3\right)}\)
Solution:
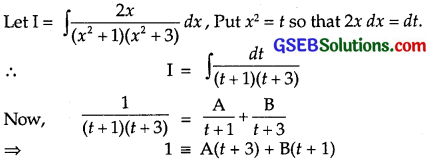
Put t = – 1, 1 = A(- 1 + 3) = 2A ∴ A = \(\frac{1}{2}\)
Put t = – 3, 1 = B(- 3 + 1) = – 2B ∴ B = – \(\frac{1}{2}\).
∴ \(\frac{1}{(t+1)(t+3)}\) = \(\frac{1}{2}\)
Integrating both sides

![]()
Question 20.
\(\frac{1}{x\left(x^{4}-1\right)}\)
Solution:

Question 21.
\(\frac{1}{e^{x}-1}\)
Solution:

Choose the correct answer in each of the following questions 22 and 23:
Question 22.
∫ \(\frac{xdx}{(x-1)(x-2)}\) equals
(A) log |\(\frac{(x-1)^{2}}{x-2}\)| + C
(B) log |\(\frac{(x-2)^{2}}{x-1}\)| + C
(C) log |(\(\frac{(x-1)^{2}}{x-2}\)| + C
(D) log |(x – 1)(x – 2)| + C
Solution:
Let \(\frac{x}{(x-1)(x-2)}\) = \(\frac{A}{x-1}\) + \(\frac{B}{x-2}\)
∴ x = A(x – 2) + B(x – 1)
Put x = 1, 1 = A(1 – 2) = – A ∴ A = – 1
Put x = 2, 2 = B(2 – 1) = B ∴ B = 2.
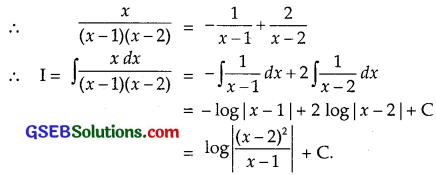
∴ Part (B) is the correct answer.
![]()
Question 23.
∫ \(\frac{d x}{x\left(x^{2}+1\right)}\) equals
(A) log|x| – \(\frac{1}{2}\) log |x2 + 1| + C
(B) log |x| + \(\frac{1}{2}\) log|x2 + 1| + C
(C) – log |x| + \(\frac{1}{2}\) log |x2 + 1| + C
(D) \(\frac{1}{2}\) log|x| + log |x2 + 1| + C
Solution:

∴ Part (A) is the correct answer.