GSEB Solutions Class 12 Maths Chapter 7 Integrals Ex 7.9

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Ex 7.9 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Ex 7.9

Evaluate the following definite integrals:
Question 1.
\(\int_{-1}^{1}\) (x + 1)dx
Solution:

Question 2.
\(\int_{2}^{3}\) \(\frac{1}{x}\) dx
Solution:

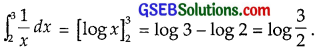
= log 3 – log 2 = log \(\frac{3}{2}\).

Question 3.
\(\int_{1}^{2}\) (4x³ – 5x² + 6x + 9) dx
Solution:

Question 4.
\(\int_{0}^{\frac{\pi}{4}}\) sin 2x dx
Solution:

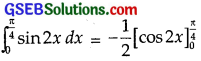
= – \(\frac{1}{2}\)(cos \(\frac{π}{2}\) – cos 0) = \(\frac{1}{2}\)

Question 5.
\(\int_{0}^{\frac{\pi}{2}}\) cos 2x dx
Solution:

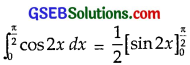
= \(\frac{1}{2}\)[sin π – sin 0] = \(\frac{1}{2}\)(0 – 0) = 0.

Question 6.
\(\int_{4}^{5}\) e^x dx
Solution:

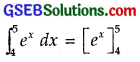
= e⁵ – e⁴ = e⁴(e – 1).

Question 7.
\(\int_{0}^{\frac{\pi}{4}}\) tanx dx
Solution:

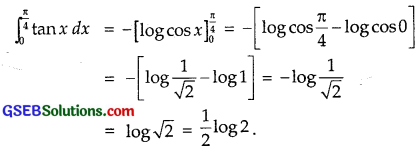
Question 8.
\(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\) cosec x dx
Solution:

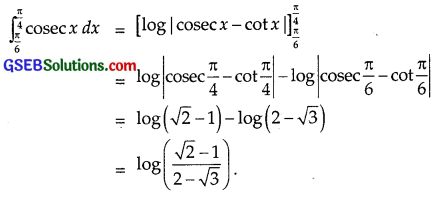
Question 9.
\(\int_{0}^{1}\) \(\frac{dx}{\sqrt{1-x^{2}}}\)
Solution:

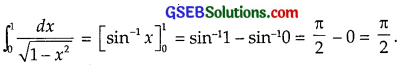
Question 10.
\(\int_{0}^{1}\) \(\frac{dx}{\sqrt{1+x^{2}}}\)
Solution:

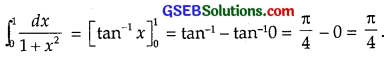
Question 11.
\(\int_{2}^{3}\) \(\frac{dx}{x^{2}-1}\)
Solution:

Question 12.
\(\int_{0}^{\frac{\pi}{2}}\) cos² x dx
Solution:

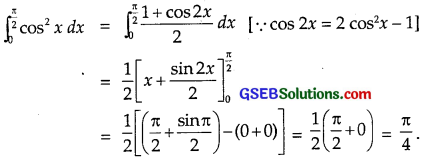
Question 13.
\(\int_{2}^{3}\) \(\frac{x d x}{x^{2}+1}\)
Solution:

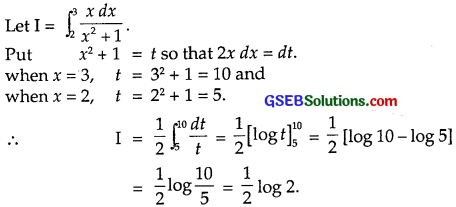
Question 14.
\(\int_{0}^{1}\) \(\frac{2 x+3}{5 x^{2}+1}\) dx
Solution:

Question 15.
\(\int_{0}^{1}\) x e^x2 dx
Solution:

Question 16.
\(\int_{1}^{2}\) \(\frac{5 x^{2}}{x^{2}+4 x+3}\) dx
Solution:

Question 17.
\(\int_{0}^{\frac{\pi}{4}}\) (2sec² x + x³ + 2) dx
Solution:

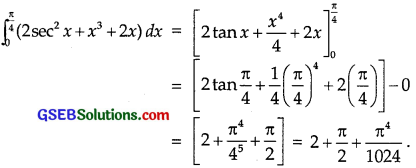
Question 18.
\(\int_{0}^{π}\)(sin² \(\frac{x}{2}\) – cos² \(\frac{x}{2}\))dx
Solution:

Question 19.
\(\int_{0}^{2}\) \(\frac{6 x+3}{x^{2}+4}\) dx
Solution:

Question 20.
\(\int_{0}^{1}\)(xe^x + sin \(\frac{πx}{2}\)) dx
Solution:

Choose the correct answers in questions 21 and 22:
21. \(\int_{1}^{\sqrt{3}}\) equals
(A) \(\frac{π}{3}\)
(B) \(\frac{2π}{3}\)
(C) \(\frac{π}{6}\)
(D) \(\frac{π}{12}\)
Solution:

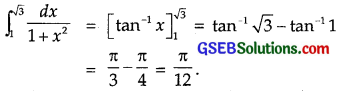
∴ Part (D) is the correct answer.

Question 22.
\(\int_{-6}^{\frac{2}{3}} \frac{d x}{4+9 x^{2}}\) equals
(A) \(\frac{π}{6}\)
(B) \(\frac{π}{12}\)
(C) \(\frac{π}{24}\)
(D) \(\frac{π}{4}\)
Solution:

∴ Part (C) is the correct answer.