Gujarat Board Statistics Class 12 GSEB Solutions Part 1 Chapter 1 Index Number Ex 1.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 1 Chapter 1 Index Number Ex 1.3
Question 1.
The information about six different items used in the production of an electronics item is as follows. Find the index number and interpret it.

Answer:
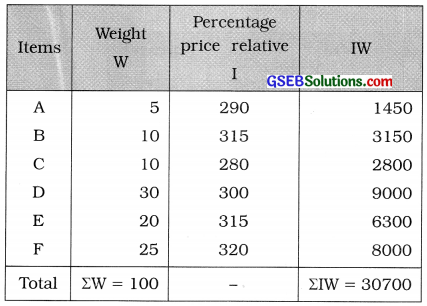
Index number I = \(\frac{\Sigma \mathrm{IW}}{\Sigma \mathrm{W}}\)
= \(\frac{30700}{100}\)
= 307
Hence, index number = 307
Interpretation: As compared to base year there is (307 – 100 =) 207% increase in the current year.

Question 2.
The information about six different items used in the furniture items is as follows. Find the index number for the year 2015 with the base year 2014 and interpret it.

Answer:
Base year: 2014
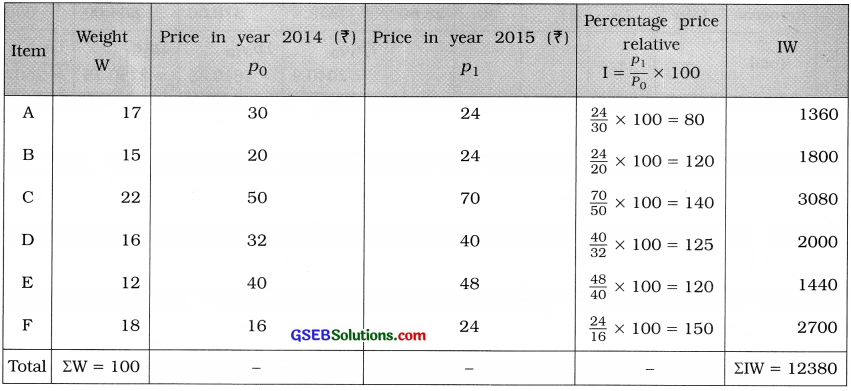
Index number I = \(\frac{\Sigma \mathrm{IW}}{\Sigma \mathrm{W}}\)
= \(\frac{12380}{100}\)
= 123.80
Interpretation : As compared to base year 2014, the Index number of the year 2015 is obtained as 123.80. Hence, there is (123.80-100=) 23.80% increase in the price of furniture.

Question 3.
Find the Laspeyre’s, Paasche’s and Fisher’s index numbers for the year 2015 with the base year 2014 using the following information:
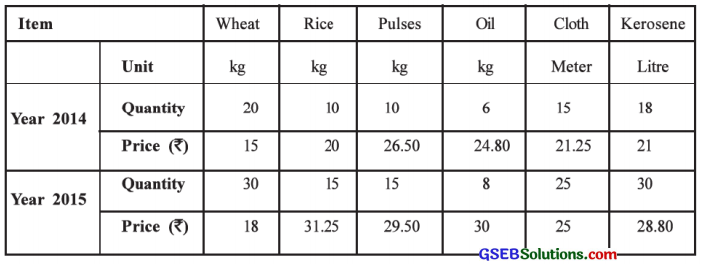
Answer:
Base year is 2014. ∴ p0 = Price in 2014, q0 = Quantity in 2014,
p1 = Price in 2015, q1 = Quantity in 2015.
To compute Laspeyre’s, Paasche’s and Fisher’s index numbers for the year 2015, the table of calculation is prepared as follows:
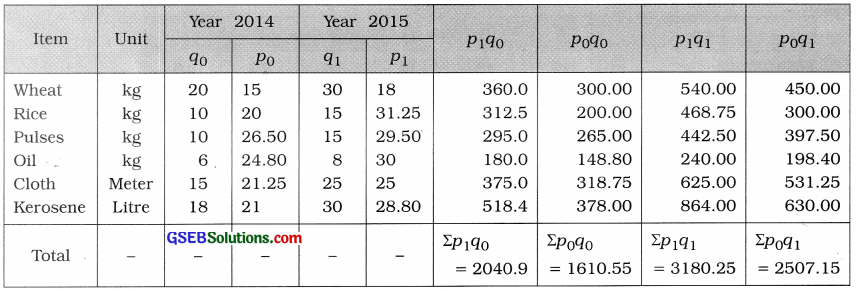
Laspeyre’s index number:
IL = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) × 100
= \(\frac{2040.9}{1610.55}\) × 100 = 1.2672 × 100 = 126.72
Paasche’s index number:
IP = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) × 100
= \(\frac{3180.25}{2507.15}\) × 100
= 1.2685 × 100 = 126.85
Fisher’s index number:
IF = \(\sqrt{\mathrm{I}_{\mathrm{L}} \times \mathrm{I}_{\mathrm{P}}}\)
= \(\sqrt{126.72 \times 126.85}\)
= \(\sqrt{16074.432}\)
= 126.78

Question 4.
Find the Laspeyre’s, Paasche’s and Fisher’s index numbers for the year 2015 with the base year 2014 using the following information:
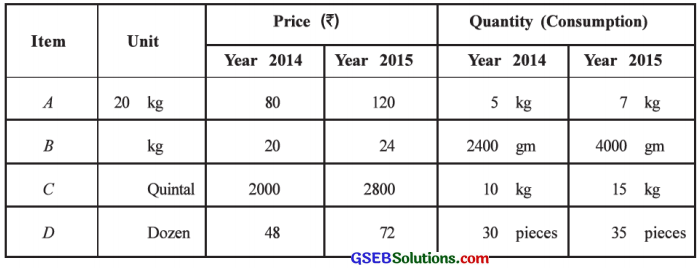
Answer:
Here, base year is 2014.
∴ p0 = Price in 2014, q0 = Quantity in 2014,
P1 = Price in 2015, q1 = Quantity in 2015.
The units of price and quantity for the items A, B, C and D are not equal. So we compute after making the units of price and quantity.
Explanation :
Item A: The unit of price is 20 kg and the unit of quantity is kg.
∴ In 2014, the price per kg = \(\frac{80}{20}\) = ₹ 4
In 2015, the price per kg = \(\frac{120}{20}\) = ₹ 6
Item B: The unit of price is kg and the unit of quantity is gram.
∴ In 2014, the quantity in kg = \(\frac{2400}{1000}\) = 2.4 kg
In 2015, the quantity in kg = \(\frac{4000}{1000}\) = 4 kg
[Note: 1000 gram = 1 kg]
Item C: The unit of price is quintal and the unit of quantity is kg.
∴ In 2014. the price per kg = \(\frac{2000}{100}\) = ₹ 20
In 2015, the price per kg = \(\frac{2800}{100}\) = ₹ 28
[Note : 1 Quintal = 100 kg]
Item D: The unit of price is dozen and the unit of quantity is a piece.
∴ In 2014, the price per piece = \(\frac{48}{12}\) = ₹ 4
In 2015, the price per piece = \(\frac{72}{12}\) = ₹ 6
[Note : 1 Dozen =12 pieces]]
To compute Laspeyre’s, Paasche’s and Fisher’s index numbers, the table of calculations is prepared as follows :
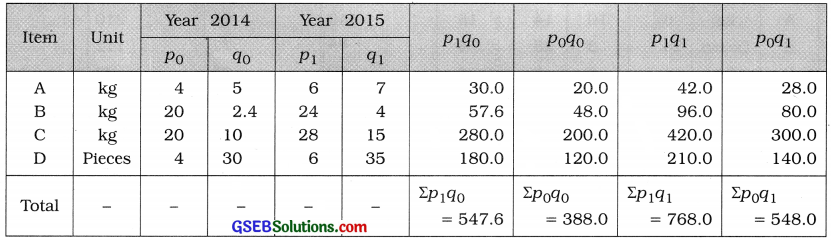
Laspeyre’s index number:
IL = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) × 100
= \(\frac{547.6}{388.0}\) × 100 = 1.4113 × 100 = 141.13
Paasche’s index number:
IP = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) × 100
= \(\frac{768.0}{548.0}\) × 100
= 1.4015 × 100 = 140.15
Fisher’s index number:
IF = \(\sqrt{\mathrm{I}_{\mathrm{L}} \times \mathrm{I}_{\mathrm{P}}}\)
= \(\sqrt{141.13 \times 140.15}\)
= \(\sqrt{19779.3695}\)
= 140.64

Question 5.
Find the ideal index number from the following data for the year 2015:
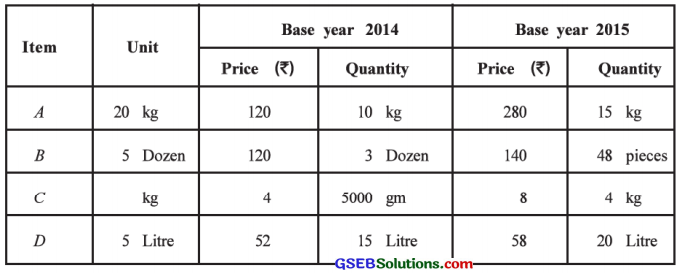
Answer:
Here, p0 = Price in 2014, q0 = Quantity in 2014,
P1 = Price in 2015, q1 = Quantity in 2015.
After making the units of price and quantity, we will compute the ideal index number, i.e., Fisher’s index number.
Explanation :
Item A: The unit of price is 20 kg and the unit of quantity is kg.
∴ In 2014. the price per kg = \(\frac{120}{20}\) = ₹ 6
In 2015, the price per kg = \(\frac{280}{20}\) = ₹ 14
Item B: The unit of price is 5 dozen and the unit of quantity is dozen.
∴ In 2014, the price per dozen = \(\frac{120}{5}\) = ₹ 24
In 2015, the price per dozen = \(\frac{140}{5}\) = ₹ 28
In 2015, the quantity in dozen = \(\frac{48}{12}\) = 4 dozen
Item C : The unit of price is kg and the unit of quantity is gram.
∴ In 2014, the quantity in kg = \(\frac{5000}{1000}\) = 5 kg
Item D : The unit of price is 5 litre and the unit of quantity is litre.
∴ In 2014, the price per litre = \(\frac{52}{5}\) = ₹ 10.40
In 2015. the price per litre = \(\frac{58}{5}\) = ₹ 11.60
To compute Fisher’s index number, the table for calculation is prepared as follows:
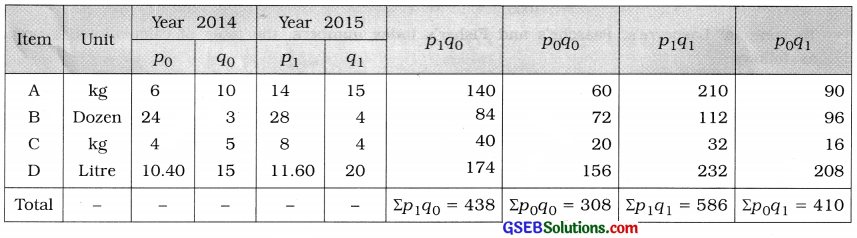
Fisher’s index number:
IF = \(\sqrt{\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times \frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}}\) × 100
= \(\sqrt{\frac{438}{308} \times \frac{586}{410}}\) × 100
= \(\sqrt{1.4221 \times 1.4293}\) × 100
= \(\sqrt{2.0326}\) × 100
= 1.4257 × 100
= 142.57

Question 6.
Find the Paasche’s and Fisher’s index numbers for the year 2015 with the base year 2014 using the data given below:
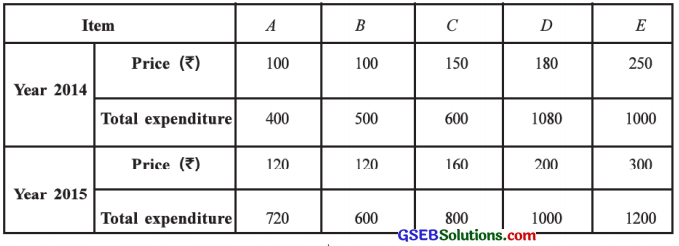
Answer:
Here, prices and total expenditure of items are given.
Total expenditure of an item = (Price per unit of an item) × (Quantity consumed of an item)
∴ Quantity consumed of an item = \(\frac{\text { Total expenditure of an item }}{\text { Price per unit of an item }}\)
From the given data using the above formula we will find the quantity consumed for each item. To compute Paasche’s and Fisher’s index number, the table for calculation is prepared as follows:
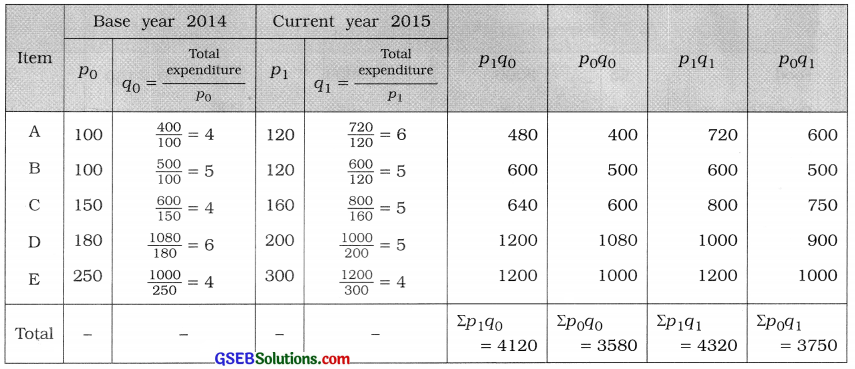
Paasche’s index number:
Ip = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) × 100
= \(\frac{4320}{3750}\) × 100
= 1.152 × 100
= 115.2
Fisher’s index number:
IF = \(\sqrt{\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times \frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}}\) × 100
= \(\sqrt{\frac{4120}{3580} \times \frac{4320}{3750}}\) × 100
= \(\sqrt{1.1508 \times 1.152}\) × 100
= \(\sqrt{1.3257}\) × 100
= 1.1514 × 100
= 115.14
Hence, Paasche’s Index number is obtained as 115.2 and Fisher’s index number is obtained as 115.14.