GSEB Solutions Class 12 Statistics Part 1 Chapter 2 Linear Correlation Ex 2.2

Gujarat Board Statistics Class 12 GSEB Solutions Part 1 Chapter 2 Linear Correlation Ex 2.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 1 Chapter 2 Linear Correlation Ex 2.2

Question 1.
From the following information obtained from a sample of 7 families of a society regarding height of father (in cm) and height of his adult son (in cm), calculate the correlation coefficient:

Answer:
Here, n = 7; x = Height of father and y = Height of son
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{1169}{7}\) = 167 cm;
ȳ = \(\frac{\Sigma y}{n}\) = \(\frac{1176}{7}\) = 168 cm;
x̄ and ȳ are Integers. So the table for calculating r is prepared as follows:

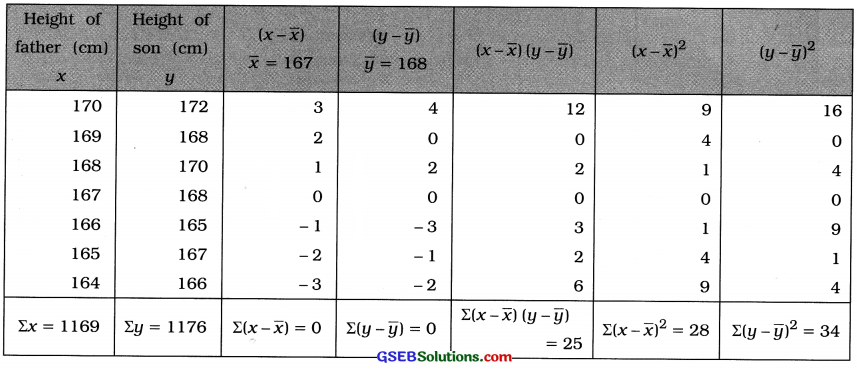
Correlation coefficient:
r = \(\frac{\Sigma(x-\bar{x})(y-\bar{y})}{\sqrt{\Sigma(x-\bar{x})^{2}} \cdot \sqrt{\Sigma(y-\bar{y})^{2}}}\)
Putting Σ(x – x̄) (y – ȳ) = 25, Σ(x – x̄)² = 28 and Σ(y – ȳ)² = 34 in the formula,
r = \(\frac{25}{\sqrt{28} \cdot \sqrt{34}}\)
= \(\frac{25}{\sqrt{952}}\)
= \(\frac{25}{30.85}\)
= 0.81

Question 2.
A local cottage industry making various snacks sells each snack in a packet of 100 gm. From a study for price determination regarding a new kind of wafer, the following information is obtained for the price and the demand:

Find the correlation coefficient between price of wafer and its demand.
Answer:
Here, n = 6; x = Price and y = Demand
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{180}{6}\) = ₹ 30; ȳ = \(\frac{\Sigma y}{n}\) = \(\frac{132}{6}\)= 22 (’000 units)
x̄ and ȳ are integers. So the table for calculating r is prepared as follows:

Correlation coefficient:
r = \(\frac{\Sigma(x-\bar{x})(y-\bar{y})}{\sqrt{\Sigma(x-\bar{x})^{2}} \cdot \sqrt{\Sigma(y-\bar{y})^{2}}}\)
Putting Σ(x – x̄) (y – ȳ) = – 79, Σ(x – x̄)² = 90 and Σ(y – ȳ)² = 86 in the formula,
r = \(\frac{-79}{\sqrt{90} \cdot \sqrt{86}}\)
= \(\frac{-79}{\sqrt{7740}}\)
= \(\frac{-79}{87.98}\)
= – 0.90
Hence, the correlation coefficient between the price and demand of wafers obtained is – 0.90.

Question 3.
From the following information of a sample of ten students of a school regarding their marks in two subjects Accountancy and Statistics, find the coefficient of correlation between the marks of two subjects:

Answer:
Here, n = 10; x = Marks in Accountancy; y = Marks in Statistics
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{640}{10}\) = 64 marks; ȳ = \(\frac{\Sigma y}{n}\) = \(\frac{610}{10}\) = 61 marks
x̄ and ȳ are integers. So the table for calculating r is prepared as follows:

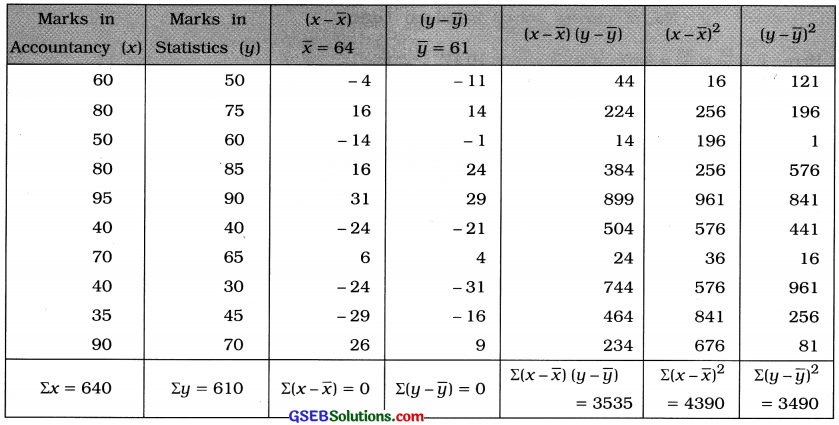
Correlation coefficient:
r = \(\frac{\Sigma(x-\bar{x})(y-\bar{y})}{\sqrt{\Sigma(x-\bar{x})^{2}} \cdot \sqrt{\Sigma(y-\bar{y})^{2}}}\)
Putting Σ(x – x̄) (y – ȳ) = 3535, Σ(x – x̄)² = 4390 and Σ(y – ȳ)² = 3490 in the formula,
r = \(\frac{3535}{\sqrt{4390} \cdot \sqrt{3490}}\)
= \(\frac{3535}{\sqrt{15321100}}\)
= \(\frac{3535}{3914.22}\)
= 0.90
Hence, the correlation coefficient between the marks of Accountancy and Statistics obtained is 0.90

Question 4.
To check the ability of Mathematics and Logic of the students of a city a private educational institute gives twenty puzzles based on these two subjects to six children selected from various schools.
The number of puzzles solved by them is given below:

Compute the correlation coefficient between performances of children in two types of puzzles using the given data.
Answer:
Here, n = 6;
x = No. of puzzles solved based on Mathematics
y = No. of puzzles solved based on Logic
Here, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{58}{6}\) = 9.67; ȳ = \(\frac{\Sigma y}{n}\) = \(\frac{61}{6}\) = 10.17
x̄ and ȳ are fractions. The values x and y are not large. So the table for calculating r is prepared as follows:

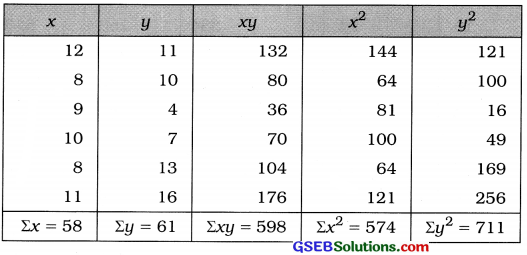
Correlation Coefficient:
r = \(\frac{n \Sigma x y-(\Sigma x)(\Sigma y)}{\sqrt{n \Sigma x^{2}-(\Sigma x)^{2}} \cdot \sqrt{n \Sigma y^{2}-(\Sigma y)^{2}}}\)
Putting n = 6, Σxy = 598, Σx = 58, Σy = 61, Σx² = 574 and Σy² = 711 in the formula,
r = \(\frac{6 \times 598-(58)(61)}{\sqrt{6 \times 574-(58)^{2}} \cdot \sqrt{6 \times 711-(61)^{2}}}\)
= \(\frac{3588-3538}{\sqrt{3444-3364} \cdot \sqrt{4266-3721}}\)
= \(\frac{50}{\sqrt{80} \cdot \sqrt{545}}\)
= \(\frac{50}{\sqrt{43600}}\)
= \(\frac{50}{208.81}\)
= 0.24
Hence, the correlation coefficient between performances of children in two types of puzzles obtained is 0.24.

Question 5.
Find the correlation coefficient between capital (in crore ₹) invested and the profit (in crore ₹) from the following data:

Answer:
Here, n = 7;. x = Capital investment; y = Profit
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{110}{7}\) = ₹ 15.71 crore; ȳ = \(\frac{\Sigma y}{n}\) = \(\frac{64}{7}\) = ₹ 9.14 crore
x̄ and ȳ are not integers and the values of x and y are not large. So the table for calculating r is prepared as follows:

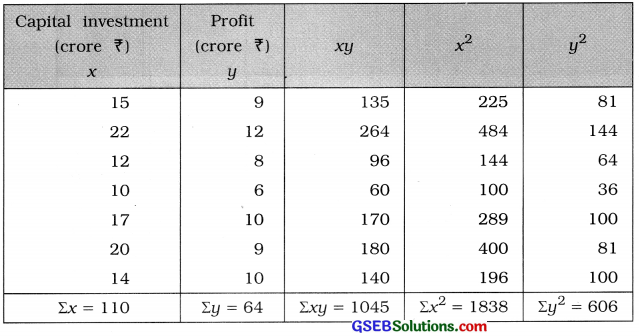
Correlation coefficient:
r = \(\frac{n \Sigma x y-(\Sigma x)(\Sigma y)}{\sqrt{n \Sigma x^{2}-(\Sigma x)^{2}} \cdot \sqrt{n \Sigma y^{2}-(\Sigma y)^{2}}}\)
Putting n = 7, Σxy = 1045, Σx = 110, Σy = 64, Σx² = 1838 and Σy² = 606 in the formula,
r = \(\frac{7 \times 1045-(110)(64)}{\sqrt{7 \times 1838-(110)^{2}} \cdot \sqrt{7 \times 606-(64)^{2}}}\)
= \(\frac{7315-7040}{\sqrt{12866-12100} \cdot \sqrt{4242-4096}}\)
= \(\frac{275}{\sqrt{766} \cdot \sqrt{146}}\)
= \(\frac{275}{\sqrt{111836}}\)
= \(\frac{275}{334.42}\)
= 0.82
Hence, the correlation coefficient between the capital investment and profit obtained is 0.82.

Question 6.
The following information is available for five students selected from a school regarding the average number of study hours per day and the average number of sleeping hours:

Calculate the correlation coefficient between the study hours and sleeping hours.
Answer:
Here, n = 5; x = No. of study hours, y = No. of sleeping hours
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{30}{5}\) = 6 hours; ȳ = \(\frac{\Sigma y}{n}\) = \(\frac{40}{5}\) = 8 hours
x̄ and ȳ are integers. So the table for calculation of r is prepared as follows:

Correlation coefficient:
r = \(\frac{n \Sigma x y-(\Sigma x)(\Sigma y)}{\sqrt{n \Sigma x^{2}-(\Sigma x)^{2}} \cdot \sqrt{n \Sigma y^{2}-(\Sigma y)^{2}}}\)
Putting Σ(x – x̄) (y – ȳ) = – 16, Σ(x – x̄)² = 28 and Σ(y – y)² = 10 in the formula,
r = \(\frac{-16}{\sqrt{28} \cdot \sqrt{10}}\)
= \(\frac{-16}{\sqrt{280}}\)
= \(\frac{-16}{16.73}\)
= – 0.96
Hence, the correlation coefficient between the study hours and sleeping hours obtained is – 0.96.

Question 7.
From the following information of the age (in years) and blood pressure (in mm), find the correlation coefficient between age and blood pressure:

Answer:
Here, n = 8; x = Age; y = Systolic blood pressure
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{464}{8}\) = 58 year; x̄ = \(\frac{\Sigma y}{n}\) = \(\frac{1153}{8}\) = 144.125 mm
x̄ is integer and ȳ is fraction. The values of x and y are large. So we calculate r by shortcut method.
Taking A = 58 and B = 150, we obtain new variables u = x – A = x – 58 and v = y – B = y – 150. The table for calculating r is prepared as follows:

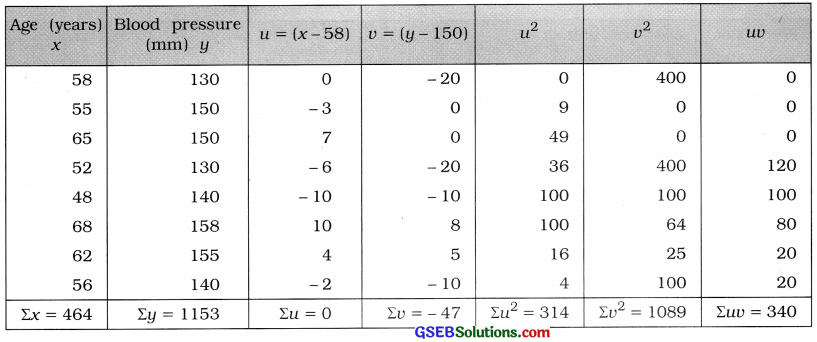
Correlation coefficient:
r = \(\frac{n \Sigma u v-(\Sigma u)(\Sigma v)}{\sqrt{n \Sigma u^{2}-(\Sigma u)^{2}} \cdot \sqrt{n \Sigma v^{2}-(\Sigma v)^{2}}}\)
Putting n = 8, luu = 340, lu = 0, ID = -47, Eu2= 314 and ID2 = 1089 in the formula,
r = \(\frac{8 \times 340-(0)(-47)}{\sqrt{8 \times 314-(0)^{2}} \cdot \sqrt{8 \times 1089-(-47)^{2}}}\)
= \(\frac{2720}{\sqrt{2512} \cdot \sqrt{8712-2209}}\)
= \(\frac{2720}{\sqrt{2512} \cdot \sqrt{6503}}\)
= \(\frac{2720}{\sqrt{16335536}}\)
= \(\frac{2720}{4041.72}\)
= 0.67
Hence, the correlation coefficient between age and blood pressure obtained is 0.67.

Question 8.
An Engineer Association wants to know the relation between the production (thousand units) and the unit production cost of different factories. The information collected from six factories regarding their production and unit production cost is given below:

Find the correlation coefficient between production and cost per unit of production.
Answer:
Here, n = 6; x = Production; y = Cost of production
Now, x̄ = \(\frac{\Sigma x}{n}\) = \(\frac{143}{6}\) = 23.83 thousand units; ȳ = \(\frac{\Sigma x}{n}\) = \(\frac{497}{6}\) = ₹ 82.83
x̄ and ȳ are not integers and values of x and y are large. Taking A = 23 for x and B = 82 for y. We obtain new variables u = x – 23 and v = y – 82. The table for calculating r is prepared as follows:

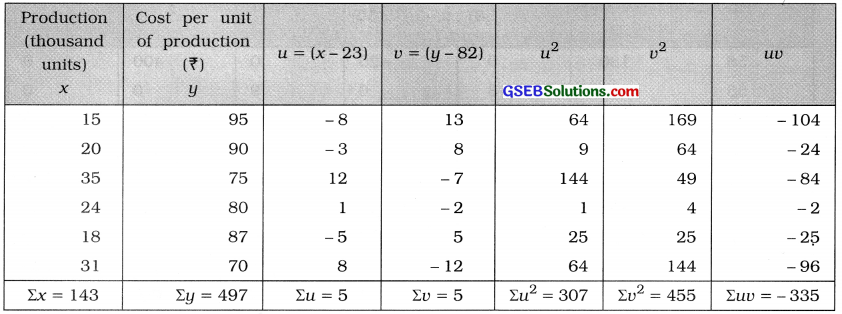
Correlation coefficient:
r = \(\frac{n \Sigma u v-(\Sigma u)(\Sigma v)}{\sqrt{n \Sigma u^{2}-(\Sigma u)^{2}} \cdot \sqrt{n \Sigma v^{2}-(\Sigma v)^{2}}}\)
Putting n = 6, Σuv = – 335, Σu = 5, Σv = 5, Σu² = 307 and Σv² = 455 in the formula,
r = \(\frac{6 \times(-335)-(5)(5)}{\sqrt{6 \times 307-(5)^{2}} \cdot \sqrt{6 \times 455-(5)^{2}}}\)
= \(\frac{-2010-25}{\sqrt{1842-25} \cdot \sqrt{2730-25}}\)
= \(\frac{-2035}{\sqrt{1817} \cdot \sqrt{2705}}\)
= \(\frac{-2035}{\sqrt{4914985}}\)
= \(\frac{-2035}{2216.98}\)
= – 0.92
Hence, the correlation coefficient between production and cost per unit of production obtained is – 0.92.

Question 9.
Find the correlation coefficient between the yearly per capita income (in ?) and the price index of the people of six different cities from the following data:

Answer:
Here, n = 6; x = Yearly per capita income; y = Price index
To make calculation of r simple and easy. We obtain new variables u and v by changing origin and scale.
The values of x are in multiple of 1000 and that of y are in multiple of 10. Therefore taking A = 30000; C_x = 1000 for x and B = 180, C_y = 10, we obtain the variables u = \(\frac{x-\mathrm{A}}{\mathrm{C}_{x}}\) = \(\frac{x-30000}{1000}\) and v = \(\frac{y-\mathrm{B}}{\mathrm{C}_{y}}\) = \(\frac{y-180}{10}\). The table for calculating r is prepared as follows:

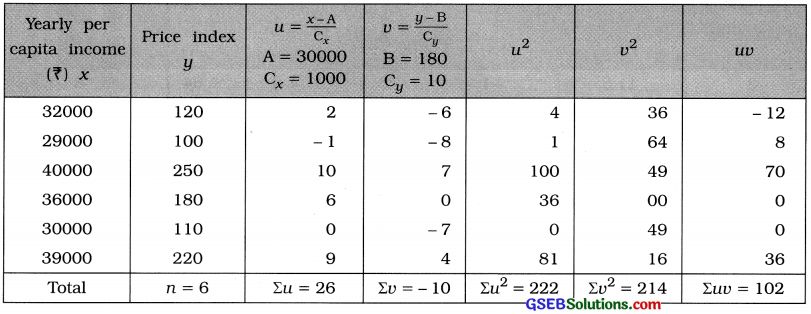
Correlation coefficient:
r = \(\frac{n \Sigma u v-(\Sigma u)(\Sigma v)}{\sqrt{n \Sigma u^{2}-(\Sigma u)^{2}} \cdot \sqrt{n \Sigma v^{2}-(\Sigma v)^{2}}}\)
Putting n = 6, Σuv = 102, Σu = 26, Σv = – 10, Σu² = 222 and Σv² = 214 in the formula,
r = \(\frac{6 \times 102-(26)(-10)}{\sqrt{6 \times 222-(26)^{2}} \cdot \sqrt{6 \times 214-(-10)^{2}}}\)
= \(\frac{612+260}{\sqrt{1332-676} \cdot \sqrt{1284-100}}\)
= \(\frac{872}{\sqrt{656} \cdot \sqrt{1184}}\)
= \(\frac{872}{\sqrt{776704}}\)
= \(\frac{872}{881.31}\)
= 0.99
Hence, the correlation coefficient between the yearly per capita income and the price index obtained is 0.99.

Question 10.
The following data are given to study the relation between the number of persons in a family who drive vehicle and usage of petrol (in litre) per week:

Find the correlation coefficient between the number of members in a family and usage of petrol.
Answer:
Here, n = 7; x = No. of members per family who drive vehicle; y = Weekly usage of petrol
To make calculation of r simple and easy, we obtain new variables.
u = \(\frac{x-\mathrm{A}}{\mathrm{C}_{x}}\); where A = 4, C_x = 1 and v = \(\frac{y-\mathrm{B}}{\mathrm{C}_{y}}\); where B = 15.5, C_y = 0.5.
The table for calculating r is prepared as follows:

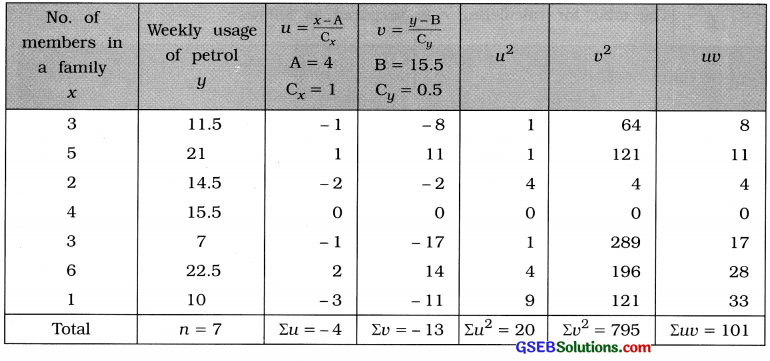
Putting n = 7, Σuv = 101, Σu = – 4, Σv = – 13, Σu² = 20 and Σv² = 795 in the formula,
r = \(\frac{7 \times 101-(-4)(-13)}{\sqrt{7 \times 20-(-4)^{2}} \cdot \sqrt{7 \times 795-(-13)^{2}}}\)
= \(\frac{707-52}{\sqrt{140-16} \cdot \sqrt{5565-169}}\)
= \(\frac{655}{\sqrt{124} \times \sqrt{5396}}\)
= \(\frac{655}{\sqrt{669104}}\)
= \(\frac{655}{817.99}\)
= 0.80
Hence, the correlation coefficient between the number of members in a family and usage of petrol obtained is 0.80.

Question 11.
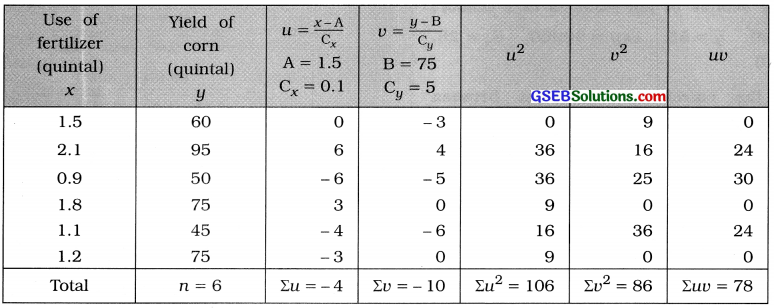
The following information is obtained to study the effect of the use of fertilizer on yield of corn in a rural area:

Find the correlation coefficient between use of fertilizer and yield of corn.
Answer:
Here, n = 6; x = Use of fertilizer; y = Yield of corn,
To make the calculation r easy and simple, we take the new variables
u = \(\frac{x-\mathrm{A}}{\mathrm{C}_{x}}\); A = 1.5, C_x = 0.1 and v = \(\frac{y-B}{C_{y}}\); B = 75, C_y = 5.
The table for calculating r is prepared as follows:

Correlation coefficient:
r = \(\frac{n \Sigma u v-(\Sigma u)(\Sigma v)}{\sqrt{n \Sigma u^{2}-(\Sigma u)^{2}} \cdot \sqrt{n \Sigma v^{2}-(\Sigma v)^{2}}}\)
Putting n = 6, Euu = 78, Zu = – 4, Eu = – 10, Su2= 106 and Eli2 = 86 in the formula,
r = \(\frac{6 \times 78-(-4)(-10)}{\sqrt{6 \times 106-(-4)^{2}} \cdot \sqrt{6 \times 86-(-10)^{2}}}\)
= \(\frac{468-40}{\sqrt{636-16} \cdot \sqrt{516-100}}\)
= \(\frac{428}{\sqrt{620} \cdot \sqrt{416}}\)
= \(\frac{428}{\sqrt{257920}}\)
= \(=\frac{428}{507.86}\)
= 0.84
Hence, the correlation coefficient between use of fertilizer and yield of corn obtained is 0.84.

Question 12.
Find the correlation coefficient from the following information of rainfall (X) (in cm) and yield (Y) (tons per hactare) for the last 10 years of a district: n = 10, Cov (x, y) = 30, S.D. of X = 5 and variance of Y = 144
Answer:
Here, n = 10; Cov (x, y) = 30; S_x = 5; S_y² = 144 Cov (x, y) ∴ S_y = 12
Now, r = \(\frac{{Cov}(x, y)}{\mathrm{S}_{x} \cdot \mathrm{S}_{y}}\)
= \(\frac{30}{5 \times 12}\) = \(\frac{30}{60}\) = 0.5
Hence, the correlation coefficient between rainfall and yield of crop obtained is 0.5.

Question 13.
The following information is obtained regarding the height (X) and weight (Y) from a sample of ten students of a school:
x̄ = 160, ȳ = 55, Σxy = 90000, S_x = 25, S_y = 10
Find the correlation coefficient between the height and weight from it.
Answer:
Here, n = 10; x̄ = 160; ȳ = 55; Σxy = 90000; S_x = 25 and S_y = 10.
Now, r =\(\frac{\Sigma x y-n \bar{x} \bar{y}}{n \cdot S_{x} \cdot S_{y}}\)
= \(\frac{90000-10 \times 160 \times 55}{10 \times 25 \times 10}\)
= \(\frac{90000-88000}{2500}\)
= \(\frac{2000}{2500}\)
= 0.8
Hence, the correlation coefficient between height and weight obtained is 0.8.

Question 14.
Determine the value of correlation coefficient from the following data:
1. Σ(x – x̄)² = 72, Σ(y – ȳ)² = 32,
Σ(x – x̄) (y – ȳ) = 45
Answer:
(1) Here, Σ(x – x̄)² = 72; Σ(y – ȳ)² = 32 and Σ(x – x̄) (y – ȳ) = 45.
= \(\frac{\Sigma(x-\bar{x})(y-\bar{y})}{\sqrt{\Sigma(x-\bar{x})^{2}} \cdot \sqrt{\Sigma(y-\bar{y})^{2}}}\)
= \(\frac{45}{\sqrt{72} \times \sqrt{32}}\)
= \(\frac{45}{\sqrt{2304}}\)
= \(\frac{45}{48}\)
= 0.94
Hence, the correlation coefficient obtained is 0.94.

(2) n = 6, Σx = 16, Σy = 51, Σxy = 154,
Σx² = 52, Σy² = 471
Answer:
Here, n = 6; Σx = 16; Σy = 51; Σxy = 154; Σx² = 52 and Σy² = 471.

Hence, the correlation coefficient obtained is 0.96.

Question 15.
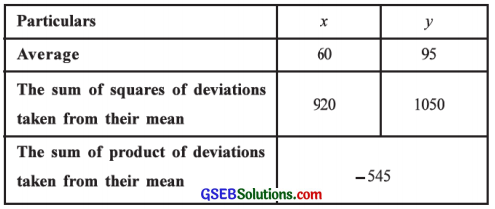
Find the value of r from the following data.

Answer:
Here, x̄ = 60; ȳ = 95; Σ(x – x̄)² = 920; Σ(y – ȳ)² = 1050 and Σ(x – x̄) (y – ȳ) = – 545.
Now, r = \(\frac{\Sigma(x-\bar{x})(y-\bar{y})}{\sqrt{\Sigma(x-\bar{x})^{2}} \cdot \sqrt{\Sigma(y-\bar{y})^{2}}}\)
= \(\frac{-545}{\sqrt{920} \cdot \sqrt{1050}}\)
= \(\frac{-545}{\sqrt{966000}}\) = \(\frac{-545}{982.85}\) = – 0.55
Hence, the correlation coefficient obtained is – 0.55.