GSEB Solutions Class 12 Statistics Part 2 Chapter 1 संभावना Ex 1

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 1 संभावना Ex 1 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 1 संभावना Ex 1

विभाग – A

निम्न दिये विकल्प प्रश्नों में से सही विकल्प पसंद करके लिखिए ।

प्रश्न 1.
निदर्श अवकाश U का विशिष्ट उपसमुच्य Φ को कौन-सी घटना कहते है?
(a) निश्चित घटना
(b) Φ की पूरक घटना
(c) U और Φ की योग घटना
(d) असंभव घटना
उत्तर :
(d) असंभव घटना

प्रश्न 2.
घटनाएँ A और A’ के लिए P(A∩A’) का मूल्य कितना होगा?
(a) 1
(b) 0
(c) 0.5
(d) 0 और 1 के बीच
उत्तर :
(b) 0

प्रश्न 3.
निदर्श अवकाश में से किसी भी घटना A के लिए निम्न में से कौन-सा विकल्प सही है?
(a) P(A) < 0
(b) 0 ≤ P(A) ≥ 1
(c) 0 ≤ P(A) ≤ 1
(d) P(A) > 1
उत्तर :
(c) 0 ≤ P(A) ≤ 1

प्रश्न 4.
निदर्श अवकाश U में से कोई दो घटनाएँ A और B के लिए A⊂B हो, तो निम्न में से कौन-सा विधान सही होगा?
(a) P(A∩B) = P(B)
(b) P(A∩B) = P(A)
(c) P(A∪B) ≥ P(A)
(d) P(B – A) = P(B) – P(A)
उत्तर :
(a) P(A∩B) = P(B)

प्रश्न 5.
संभावना की प्रशिष्ट परिभाषा दूसरे कौन-से नाम से पहचानी जाती है?
(a) गाणितिक परिभाषा
(b) पूर्व धारणायुक्त परिभाषा
(c) सांख्यिकीय परिभाषा
(d) भौमितिक परिभाषा
उत्तर :
(a) गाणितिक परिभाषा

प्रश्न 6.
एक समतुलित सिक्के को उछालने के यादृच्छिक प्रयोग में मिलती प्राथमिक घटनाएँ H और T के लिए संभावना का निम्न में से कौन-सा विधान सत्य नहि है?
(a) P(T) = 0.5
(b) P(H) + P(T)= 1
(c) P(H∩T) = 0.5
(d) P(H) = 0.5
उत्तर :
(c) P(H∩T) = 0.5

प्रश्न 7.
निम्न दर्शाया गया याद्दच्छिक प्रयोग में से कौन-सा याद्दच्छिक प्रयोग का निदर्श अवकाश अनंत है?
(a) दो पासा उछालना
(b) ऑफिस में से दो कर्मचारी चुनना
(c) इलेक्ट्रिक बल्ब का आयु घण्टे में मापना
(d) 52 पत्तों में से एक पत्ता चुनना
उत्तर :
(c) इलेक्ट्रिक बल्ब का आयु घण्टे में मापना

प्रश्न 8.
घटना A∪A’ == U हो, तो A और A’ कैसी घटनाएँ कहलायेगी ?
(a) निरपेक्ष घटनाएँ
(b) पूरक घटनाएँ
(c) निश्चित घटनाएँ
(d) असंभव घटनाएँ
उत्तर :
(b) पूरक घटनाएँ

प्रश्न 9.
यदि P(A/B) = P(A) और (B/A) = P(B) हो, तो घटनाएँ A और B कैसी घटनाएँ कहलायेंगी?
(a) निरपेक्ष घटनाएँ
(b) पूरक घटनाएँ
(c) निश्चित घटनाएँ
(d) असंभव घटनाएँ
उत्तर :
(a) निरपेक्ष घटनाएँ

प्रश्न 10.
निदर्श अवकाश की दो घटनाएँ A और B परस्पर निवारक घटनाएँ है। P(B – A) निम्न में से किसके समान है?
(a) P(A)
(b) P(B)
(c) P(A∩B)
(d) P(A∪B)
उत्तर :
(b) P(B)

प्रश्न 11.
छ भुजावाले तीन संतुलित पासा एकसाथ उछाला जाय तो, निदर्श अवकाश में निदर्श बिंदुओं की कुल संख्या कितनी होगी?
(a) 6²
(b) 3⁶
(c) 6 × 3
(d) 6³
उत्तर :
(d) 6³

प्रश्न 12.
प्राकृतिक संख्याएँ 1 और 20 के बीच की संख्याओं में से एक संख्या यादृच्छिकरीतिसेचयन किया जाय तो,वहसंख्या 5 की गुणक
होने की संभावना कितनी होगी?
(a) \(\frac {1}{2}\)
(b) \(\frac {1}{6}\)
(c) \(\frac {1}{5}\)
(d) \(\frac {1}{3}\)
उत्तर :
(b) \(\frac {1}{6}\)

प्रश्न 13.
दो घटनाएँ A और B निरपेक्ष हो, तो निम्न में से कौन-सा विकल्प सही है?
(a) P(A∩B) = P(A) × P(B)
(b) P(A∪B) = P(A) + P(B)
(c) P(A∪B) = P(A) × P(B)
(d) P(A∩B) = P(A) + P(B)
उत्तर :
(a) P(A∩B) = P(A) × P(B)

प्रश्न 14.
लीप वर्ष न हो ऐसे वर्ष में फरवरी मास में 5 गुरुवार आये उसकी संभावना कितनी होगी?
(a) 0
(b) \(\frac {1}{7}\)
(c) \(\frac {2}{7}\)
(d) \(\frac {3}{7}\)
उत्तर :
(a) 0

प्रश्न 15.
निदर्श अवकाश की दो निरपेक्ष घटनाएँ A और B के लिए P(A)= 0.4 और P(B’) = 0.3 हो, तो P(A∩B) का मूल्य बताइए।
(a) 0.12
(b) 0.42
(c) 0.28
(d) 0.18
उत्तर :
(c) 0.28

प्रश्न 16.
निदर्श अवकाश की दो घटनाएँA और B के लिए घटना (A∩B)∪(A∩B’) बताइए।
(a) Φ
(b) B
(c) A
(d) U
उत्तर :
(c) A

प्रश्न 17.
संभावना की गाणितिक परिभाषा अनुसार याद्दच्छिक प्रयोग के n परिणाम में से प्रत्येक परिणाम की संभावना कितनी होगी?
(a) 0
(b) 1/n
(c) 1
(d) कुछ नहि कहा जा सकता
उत्तर :
(b) 1/n

विभाग – B

निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए ।

प्रश्न 1.
यादृच्छिक प्रयोग के दो उदाहरण दीजिए।
उत्तर :

1. सिक्के को उछालने का प्रयोग
2. संतुलित पासे को उछालने का प्रयोग
3. तास की गड्डी में से याद्दच्छिक रूप से पत्ता चुनने का प्रयोग

प्रश्न 2.
A और B की अंतर घटना A – B की वेन आकृति खींचिए।
उत्तर :

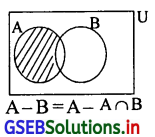
प्रश्न 3.
घटना की परिभाषा दीजिए।
उत्तर :
याद्दच्छिक प्रयोग के निदर्श अवकाश के उपसमुच्चय को घटना कहते है।

प्रश्न 4.
एक संतुलित पासा और संतुलित सिक्के को एकसाथ उछालने के यादृच्छिक प्रयोग का निदर्श अवकाश लिखिए।
उत्तर :
एक पासे और एक सिक्के को एकसाथ उछालने पर (6 × 2)= 12 परिणाम प्राप्त हो सकते है।
∴ निदर्श अवकाश U = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}

प्रश्न 5.
शर्ती संभावना की परिभाषा दीजिए।
उत्तर :
माना कि U एक निदर्श अवकाश है तथा A और B ये U की कोई दो घटनाएँ है। “घटना A घटती है” इस शर्ताधीन घटना B के घटने की संभावना को शर्ती संभावना कहते है।

प्रश्न 6.
तीन घटनाएँ A,B,C में से कम से कम एक घटना बने उसकी संभावना प्राप्त करने का सूत्र लिखिए।
उत्तर :
तीन घटना A, B और C के योग का नियम पर से P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(A∩C) – P(B∩C) + P(A∩B∩C)

प्रश्न 7.
निरपेक्ष घटना की परिभाषा लिखिए।
उत्तर :
माना कि U यह निदर्श अवकाश की A और B कोई दो घटना है। यदि घटना A बनने की संभावना घटना B घटने (या न घटने) पर कोई प्रभाव न डाले तो A और B को निरपेक्ष घटनाएँ कहते है।

प्रश्न 8.
निदर्श अवकाश की दो निरपेक्ष घटनाएँ A और B के लिए संभावना के गुणाकार का नियम लिखिए।
उत्तर :
A और B निरपेक्ष घटनाएँ हो, तो गुणाकार का नियम P(A∩B) = P(A) × P(B)

प्रश्न 9.
P(AIB) और P(B/A) का अर्थघटन लिखिए।
उत्तर :
P(A/B) = घटना B घट चुकी है उसी शर्ताधीन A बने उसकी संभावना
P(B/A)= घटना A घट चुकी है उसी शर्ताधीन B बने उसकी संभावना

प्रश्न 10.
निदर्श अवकाश U की तीन घटनाएँ A,B और C निःशेष घटनाएँ कब कहलायेगी?
उत्तर :
यदि तीनों घटनाओं की योग घटना U बने तब अर्थात् A∪B∪C = U = 1 हो तब तीन घटनाएँ A, B और C निःशेष घटनाएँ कहलायेगी।

प्रश्न 11.
P(A∪B), P(A), P(A∩B), 0, P(A) + P(B) को चढ़ते क्रम मे गठित कीजिए।
उत्तर :
चढ़ते क्रम में 0, P(A∩B), P(A), P(A∪B) + P(A) + P(B)

प्रश्न 12.
परिभाषा दीजिए।
(1) याद्दच्छिक प्रयोग
(2) निदर्श अवकाश
(3) समसंभावी घटनाएँ
(4) सानुकूल परिणाम
(5) संभावना (गाणितिक परिभाषा)
(6) संभावना (सांख्यिकीय परिभाषा)
(7) असंभव घटना
(8) निश्चित घटना
उत्तर :
(1) यादृच्छिक प्रयोग : जिस प्रयोग में समग्र प्रासंभाव्य परिणामों का वर्णन पहले से किया जा सकता है, लेकिन प्रयोग के अंत में कौन-सा परिणाम मिलेगा वह पहले से निश्चित रूप से नहीं कहा जा सकता उसे याद्दच्छिक प्रयोग (Random Experiment) कहते है।

(2) निदर्श अवकाश : किसी भी याद्दच्छिक प्रयोग के संभव सभी परिणामों के समुच्चय को उस याद्दच्छिक प्रयोग का निदर्श अवकाश कहते है।

(3) समसंभावी घटनाएँ : दो या दो से अधिक यादृच्छिक घटनाओं मे से किसी एक घटना के घटने की संभावना दूसरी घटनाओं के घटने या घटने की संभावना से कम या अधिक होने का कोई कारण न हो ऐसी घटनाओं को समसंभावी घटनाएँ (Equi-probable events) कहते है।

(4) सानुकूल परिणाम : किसी याद्दच्छिक प्रयोग की निदर्श अवकाश के प्राथमिक परिणामों में से जितने परिणामों से घटना A बने उस परिणामों की संख्याओं के योग को घटना A के लिए सानुकूल परिणाम कहेंगे।

(5) संभावना(गाणितिक परिभाषा): यदि एक याद्दच्छिक प्रयोग का निदर्श अवकाशU हो जिसके U निःशेष, परस्पर पूरक, समसंभावी परिणामों की कुल संख्या n हो जिसमें से m परिणाम घटना-A के लिए सानुकूल हो, तो घटना A के घटने की संभावना m/n होगी।
उसे संकेत में P(A) से निर्देशित किया जाता है। ∴ P(A) = m/n

(6) संभावना (सांख्यिकीय परिभाषा): माना कि किसी एक याद्दच्छिक प्रयोग का एक ही समान परिस्थिति में n बार पुनरावर्तन किया जाता है। इस n प्रयत्नों में से m प्रयत्नों में कोई एक घटना A घटती है तो इस घटना की सापेक्ष आवृत्ति m/n हो तो घटना A घटने की संभावना P(A) का अनुमानित मान कहेंगे। जबn का मान अनन्त की ओर जायेगा, तब घटनाA की संभावना P(A) यह m/n लक्षित मान धारण करेगा।

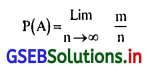
(7) असंभव घटनाः जो घटना कभी घटे ही नहीं उस घटना को असंभव घटना कहते है। जिसे रिक्त समुच्चय कहेंगे तथा Φ संकेत से निदर्श करेंगे।

(8) निश्चित घटना : याद्दच्छिक प्रयोग के परिणाम के रूप में जो घटना हमेशा घटती हो, उस घटना को निश्चित घटना कहते है।

प्रश्न 13.
निदर्श अवकाश की दो घटनाएँA और B के लिए A∩B = Φ और A∪B = U हो,तो P(A∩B) और P(A∪B) का मूल्य बताइए।
उत्तर :
P(A∩B) = 0 और P(A∪B) = 1 होगा।

प्रश्न 14.
निदर्श अवकाश की दो घटनाएँ A और B निरपेक्ष घटनाएं हो, तो P(A∪B) का सूत्र लिखो।
उत्तर :
A और B निरपेक्ष घटनाएँ है इसलिए P(A∩B) = P(A) × P(B) ∴ P(A∪B) = P(A) + P(B) – P(A) × P(B)

प्रश्न 15.
A = {x/0 < x < 1} तथा B = {x/\(\frac {1}{4}\) ≤ x ≤ 3}हो, तो A∩B ज्ञात कीजिए।
उत्तर :
A∩B = (x/\(\frac {1}{4}\) ≤ x ≤ 1)

प्रश्न 16.
निरपेक्ष घटनाएँA और B के लिए P(A)= 0.5 और P(B) = 0.7 हो, तो P(A’∩B’) ज्ञात कीजिए।
उत्तर :
A और B निरपेक्ष घटना है इसलिए A’ और B’ भी निरपेक्ष घटनाएँ होती है
∴ P(A’) = 1 – P(A) = 1 – 0.5, P(A’) = 0.5 P(B’)= 1 – P(B) = 1 – 0.7 = 0.3
∴ P(A’∩B’) = P(A’) × P(B’) = 0.5 × 0.3 = 0.15

प्रश्न 17.
यदि P(A)= 0.8 और P(A∩B) = 0.25 हो, तो P(A – B) ज्ञात कीजिए।
उत्तर :
P(A – B) = P(A) – P(A∩B) = 0.8 – 0.25 ∴ P(A – B) = 0.55

प्रश्न 18.
यदि P(A) = 0.3 और P(A∩B) = 0.03 हो, तो P(B/A) ज्ञात कीजिए।
उत्तर :
P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{0.03}{0.3}\)
∴ P(B/A) = 0.1

प्रश्न 19.
परस्पर निवारक दो घटनाएँ A और B के लिए P(A) = P(B) = k हो, तो P(A∪B) ज्ञात कीजिए।
उत्तर :
परस्पर निवारक घटनाएँ के लिए योग का नियम
P(A∪B) = P(A) + P(B) = k + k ∴ P(A∪B) = 2k
P(A) = P(B) =k ∴ P(A) = k P(B) = k

प्रश्न 20.
यदि P(A’∩B) = 0.45 और A∩B = Φ हो, तो P(B) ज्ञात करो।
उत्तर :
P(A’∩B) = P(B) – P(A∩B) 0.45 = P(B) – 0 ∴ P(B) = 0.45

प्रश्न 21.
निदर्श अवकाश की दो घटनाएँ A और B परस्पर निवारक और निःशेष है। यदि P(A) = 1/3 हो, तो P(B) ज्ञात कीजिए।
उत्तर :
A और B परस्पर निवारक और निःशेष घटनाएँ है इसलिए
P(A∪B) = P(A) + P(B) = \(\frac {1}{3}\) + P(B) = 1 ∴ P(B) = 1 – \(\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\) P(B) = \(\frac {2}{3}\)

प्रश्न 22.
एक समूह के 2% इकाई दोषयुक्त है।इस समूहमें से याद्दच्छिकरीति से चयन की गई एक इकाई दोष रहित होने की संभावना के मान
की गणना कीजिए।
उत्तर :
दोष युक्त हो उसे घटना A कहे तो P(A) = \(\frac {2}{100}\) = 0.02 दोष रहित हो अर्थात् दोष युक्त की पूरक घटना बनेगी उसे P(A’) कहे तो
P(A) = 1 – P(A’)
∴ P(A’)= 1 – P(A) = 1 – 0.02 = 0.98 दोष रहित की संभावना = 0.98

प्रश्न 23.
पांच संतुलित सिक्के को उछालने के याद्दच्छिक प्रयोग के निदर्श बिंदुओं की संख्या बताइये।
उत्तर :
पांच संतुलित सिक्के को उछालने के निदर्श बिंदुओं की संख्या n = 2⁵ = 2 × 2 × 2 × 2 × 2 = 32

प्रश्न 24.
एक संतुलित सिक्के और दो संतुलित पासा एकसाथ उछालने के यादृच्छिक प्रयोग में निदर्श बिंदुओं की संख्या ज्ञात कीजिए।
उत्तर :
एक संतुलित सिक्के को उछालने पर 2′ = 2 परिणाम दो संतुलित पासे को उछालने पर 6² = 36
परिणाम दोनों को साथ में उछालने के निदर्श बिंदुओं की कुल संख्या = 2 × 36 =72

प्रश्न 25.
निदर्श अवकाश की दो घटनाएँ A और B के लिए P(A)= 0.7 और P(A∪B) = 0.45 संभव है? कारण दीजिए।
उत्तर :
संभव नहि है क्योंकि P(A∪B) < P(A) होना चाहिए। यहाँ P(A) = 0.7 दिया है और P(A∪B) = 0.45 है।

प्रश्न 26.
52 तास के पत्तों में से यादृच्छिक रीति से दो पत्ते पूर्ति सहित एक के पश्चात् एक चयन किया जाता है। इस यादृच्छिक प्रयोग के निदर्श अवकाश के घटकों की संख्या लिखिए।
उत्तर :
एक के पश्चात् एक पत्ता पूर्ति सहित चयन करने के घटकों की संख्या n = ₅₂C₁ × ₅₂C₁ = 52 × 52 = 2704 ∴ n = 2704

प्रश्न 27.
दो निरपेक्ष घटनाएँ A और B के लिए P(B/A) = \(\frac {1}{2}\) और P(A∩B)= \(\frac {1}{5}\) हो, तो P(A) ज्ञात कीजिए।
उत्तर :
दो घटनाएँ निरपेक्ष है इसलिए P(B/A) = P(B)

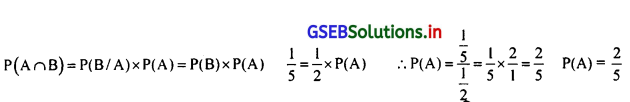
प्रश्न 28.
2000 टिकट में से 1998 टिकट बिना इनामवाली है। एक व्यक्ति 2000 टिकट में से एक टिकट यादृच्छिक रीति से चयन करे तो, चयन की गई टिकट ईनामपात्र हो उसकी संभावना कितनी होगी?
उत्तर :
1998 टिकट बिना ईनामवाली है इसलिए (2000 – 1998) = 2 ईनामपात्र है। कुल 2000 टिकट में से एक टिकट चयन करने का निदर्श
अवकाश n = ²⁰⁰⁰C₁ = 2000 ईनामपात्र टिकट को घटना A कहे तो A के लिए सानुकूल परिणाम m = ²C₁ = 2
∴ P(A) = \(\frac{m}{n}=\frac{2}{2000}=\frac{1}{1000}\)
मांगी गई संभावना = \(\frac{1}{1000}\)

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
निम्न घटनाओं के लिए वेन आकृति बनाकर उसकी परिभाषा लिखिए।
(1) परस्पर निवारक घटनाएँ
(2) संघ घटना
(3) प्रतिच्छेद घटना
(4)अंतर घटना
(5)निःशेष घटनाएँ
(6) पूरक घटनाएँ
उत्तर :
(1) परस्पर निवारक घटनाएँ:

मानाकि U सान्त निदर्श अवकाश की A और B कोई दो घटनाएँ है। यदि A∩B = Φ हो, तो घटनाएँ A और B परस्पर निवारक घटनाएँ है।

(2) संघ घटनाः
यदि A और B निदर्श अवकाश U की कोई दो घटनाएँ है। घटना A घटे या घटना B घटे याA और B दोनों घटनाएँ एकसाथ घटे उस घटना को A और B की संघ घटना कहेंगे। जिसे संकेत में A∪B से निर्देशित करेंगे।

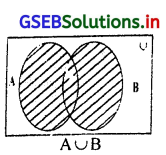
(3) प्रतिच्छेद घटना:
मानाकि A और B निदर्श अवकाश U की कोई दो घटनाएँ है। “घटना A और B दोनों साथ बने” उसे A और B की प्रतिच्छेद घटना कहते है। उसे संकेत में A∩B से निर्देशित किया जाता है।

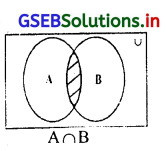
(4)अंतर घटना:
अंतर घटना A – B और B – A, मानाकि A और B निदर्श अवकाश U की कोई दो घटनाएँ है। “घटनाA घटे परंतु B नघटे” ऐसे निदर्श अवकाश की समग्र घटनाओं से रचित समुच्य को A और B की अंतर घटना कहते है। उसी तरह घटनाB घटे परंतु A न घटे ऐसे निदर्श अवकाश की समग्र घटनाओं से रचित समुच्य को B और A की अंतर घटना कहते है जिसे संकेत में B – A से निर्देशित किया जाता है।

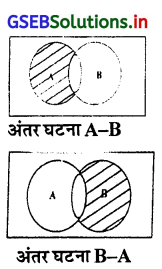
(5)निःशेष घटनाएँ:
यदि याद्दच्छिक प्रयोग की घटनाएँ में से संभवतः परिणाम का समूह निदर्श अवकाश हो तो उस घटनाओं को निःशेष घटनाएँ कहते है। मानाकि A और B निदर्श अवकाश U की कोई दो घटनाएँ हो और घटना A∪B = U हो, तो A और B को निःशेष घटनाएँ कहते है।

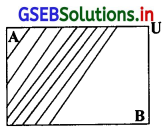
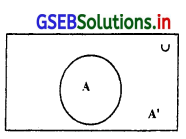
(6) पूरक घटनाएँ:
यदि A निदर्श अवकाश U की कोई एक घटना हो, तो घटना A न घटे अर्थात् A में न ऐसे निदर्श अवकाश U के परिणामों से घटते समुच्य को घटना A की पूरक घटना कहते है जिसे संकेत में A’ द्वारा निर्देशित करते है।

प्रश्न 2.
सान्त और अनंत निदर्श अवकाश के उदाहरण दीजिए।
उत्तर :
सान्त निदर्श अवकाश के उदाहरणः

1. एक संतुलित सिक्के को उछालने से प्राप्त परिणाम H और T
2. एक संतुलित पासे को उछालने से प्राप्त परिणाम 1, 2, 3, 4, 5, 6 U= {1, 2, 3, 4, 5, 6}

अनंत निदर्श अवकाश के उदाहरणः

1. उत्पादित ईलेक्ट्रीक बल्ब का आयुष्य घण्टों में मापा जाय तो परिणाम 0 से अधिक होगा।
2. छाप मिले तब तक सिक्के को उछालने का प्रयोग

प्रश्न 3.
असंभव और निश्चित घटना के उदाहरण दीजिए।
उत्तर :
असंभव घटना के उदाहरण :

1. सिक्के को उछालने पर उस पर H और T दोनों मिले यह असंभव है।
2. काली गेंद भरी टोकरी में से एक गेंद चयन करने पर लाल गेंद मिले यह असंभव घटना है।

निश्चित घटना के उदाहरण :

1. शनिवार के बाद तुरंत का वार रविवार आये
2. एक संतुलित पासे को उछालने पर पासा पर का अंक 7 से कम आये

प्रश्न 4.
यादृच्छिक प्रयोग के लक्षण बताइए।
उत्तर :
यादृच्छिक प्रयोग के लक्षण :

1. यादृच्छिक प्रयोगों का समान परिस्थिति के अधीन पुनरावर्तन संभव है।
2. याद्दच्छिक प्रयोग के समग्र प्रासंभाव्य परिणाम कौन-कौन से हैं, तत्सम्बन्धित सूचना प्राप्त होती है।
3. याद्दच्छिक प्रयोग के समग्र प्रासंभाव्य परिणामों मे से कौन-सा परिणाम मिलेगा, इसका निश्चित अनुमान प्रयोग के पूर्व नहीं किया जा सकता।

प्रश्न 5.
संभावना की गाणितिक परिभाषा की धारणाएँ लिखिए।
उत्तर :
संभावना की गाणितिक परिभाषा की धारणाएँ निम्नानुसार है :

1. याद्दच्छिक प्रयोग के निदर्श अवकाश के परिणाम की संख्या सान्त है।
2. याद्दच्छिक प्रयोग के निदर्श अवकाश के कुल परिणामों की संख्या ज्ञात है।
3. यादृच्छिक प्रयोग के निदर्श अवकाश के परिणाम समसंभावी है।

प्रश्न 6.
संभावना की गाणितिक परिभाषा की मर्यादाएँ लिखिए।
उत्तर :
संभावना की गाणितिक परिभाषा की मर्यादाएँ निम्नलिखित है :

1. याद्दच्छिक प्रयोग के निदर्श अवकाश के परिणामों की संख्या अनंत हो तो यह परिभाषा से संभावना ज्ञात नहि हो सकती है।
2. यादृच्छिक प्रयोग के निदर्श अवकाश के कुल परिणामों की संख्या जानते न हो तो यह परिभाषा से घटना की संभावना ज्ञात नहीं हो सकती है।
3. याद्दच्छिक प्रयोग के निदर्श अवकाश की प्राथमिक घटनाएँ समसंभावी न हो तो किसी भी घटना की संभावना इस परिभाषा से ज्ञात नहीं हो सकती है।
4. संभावना की गाणितिक परिभाषा में ‘समसंभावी’ शब्द का प्रयोग किया गया है। समसंभावी अर्थात् समान संभावनावाली घटनाएँ। संभावना की परिभाषा में ही संभावना शब्द का उपयोग किया गया है।

प्रश्न 7.
संभावना की सांख्यिकीय परिभाषा की मर्यादाएँ लिखिए।
उत्तर :
संभावना की सांख्यिकीय परिभाषा की मर्यादायें निम्नानुसार है :

1. संभावना की सांख्यिकीय परिभाषा में n – α अर्थात् n का मूल्य अनंत को अनुलक्षित हो तब ही संभावना का मूल्य प्राप्त होता है लेकिन व्यवहार में n का मूल्य अनंत नहि लिया जा सकता।
2. इस परिभाषा से प्राप्त किसी भी घटना की संभावना एक अंदाजित मूल्य है यह परिभाषा की सहायता से संभावना की सही किंमत जान सकते नहीं है।

प्रश्न 8.
समसंभावी घटनाएं उदाहरण देकर समझाइए।
उत्तर :
किसी याद्दच्छिक प्रयोग के निदर्श अवकाश की दो या उससे अधिक घटनाओं में से एक घटना के घटने की संभावना दूसरी घटनाओं के घटने या न घटने की संभावना से कम या अधिक होने का कोई कारण न हो ऐसी घटनाओं को समसंभावी घटनाएँ कहते है। उदा. एक सिक्के को उछालने के प्रयोग में छाप (H) और काँटा (T) निर्देशित प्राथमिक घटनाओं को समसंभावी घटनाएँ कहते है।

प्रश्न 9.
निदर्श अवकाश की दो घटनाएँ A और B के लिए संभावना के योग का नियम लिखिए। यदि यह घटनाएँ परस्पर निवारक हो, तो संभावना के योग का नियम लिखिए।
उत्तर :
निदर्श अवकाश की दो घटनाएँ A और B के लिए योग का नियम P(A∪B) = P(A) + P(B) – P(A∩B)
A और B परस्पर निवारक हो तो योग का नियम A∩B = Φ P(A∪B) = P(A) + P(B)

प्रश्न 10.
निदर्श अवकाश की दो घटनाएँA और B के लिए संभावना का गुणाकार का नियम लिखिए।यदिघटनाएँA और B निरपेक्ष हो तब संभावना के गुणाकार का नियम लिखिए ।
उत्तर :
दो घटनाएँA और B के लिए गुणाकार का नियम P(A∩B) = P(A) × P(B/A); P(A) ≠ Φ
P(A∩B) = P(B) × P(A / B)j P(B) ≠ 0 यदिA और B निरपेक्षघटनाएँ हो तो गुणाकार का नियम P (A∩B) = P(A) × P(B)

प्रश्न 11.
निदर्श अवकाश की दो निरपेक्ष घटनाओं A और B के लिए निम्न परिणाम लिखिए।
(1) P(A∩B)
(2) P(A’∩B’)
(3)P(A∩B’)
(4)P(A’∩B)
उत्तर :
निदर्श अवकाश की दो घटनाएँ निरपेक्ष है इसलिए A’ और B’ भी निरपेक्ष होती है। इसलिए
(1) P(A∩B) = P(A) × P(B)
(2) P(A’∩B’) =P(A’) × P(B’)
(3) P(A∩B’) = P(A) × P(B’)
(4)P(A’∩B) = P (A’) × P(B)

प्रश्न 12.
यदि P(A)= \(\frac {1}{3}\) P(B) = \(\frac {2}{3}\) और P(A∩B)= \(\frac {1}{6}\) हो, तो P(A’∩B’) ज्ञात कीजिए।
उत्तर :
P(A’∩B’) = 1 – P(A∪B) सूत्र का उपयोग करेंगे। इसके लिए प्रथम P(A∪B) ज्ञात करेंगे।
योग के नियम के अनुसार

मांगी गई संभावना = \(\frac {1}{6}\)

प्रश्न 13.
यदि P(B) = 2P(A/B) = 0.4 हो, तो P(A∩B) ज्ञात कीजिए।
उत्तर :
P(B) = 2P(A/B) = 0.4 दिया है।
∴ P(B) = 0.4 2P(A/B) = 0.4 ∴ P(A/B) = \(\frac{0.4}{2}\) P(A/B) = 0.2
शर्ती संभावना के नियम अनुसार
P(A/B) = \(\frac{P(A \cap B)}{P(B)}\) = 0.2 = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{0.4}\) 0.2 × 0.4 = P(A∩B)
∴ P(A∩B) = 0.08
मांगी गई संभावना = 0.08

प्रश्न 14.
घटनाएँ A और B निरपेक्ष घटनाएं हो और 3R(A) =2P(B) = 0.12 हो, तो P(A∩B) ज्ञात कीजिए।
उत्तर :
A और B निरपेक्ष घटनाएँ है।
3P(A) = 2P(B) = 0.12
3P(A) = 0.12
P(A)= \(\frac{0.12}{3}\)
∴ P(A)= 0.4

2P(B) = 0.12
P(B) = \(\frac{0.12}{2}\)
∴ P(B) = 0.06

P(A∩B) = P(A) × P(B) = 0.04 × 0.06 = 0.0024
मांगी गई संभावना = 0.0024

प्रश्न 15.
दो घटनाएँ A और B के लिए 5P(A) = 3P(B) = 2P(A∪B) = \(\frac {3}{2}\) हो, तो A(A’∩B’) ज्ञात कीजिए।
उत्तर :
दो घटनाएँ A और B के लिए 5P (A) = 3P(B) = 2P(A∪B) = \(\frac {3}{2}\) दिया है।

योग के नियम के अनुसार
P(AUB) = P(A) + P(B) – P(A∩B)

प्रश्न 16.
दो निरपेक्ष घटनाएँ A और B के लिए P(A∩B) = 0.12 और P(B) = 0.3 हो, तो P(A∪B) ज्ञात कीजिए।
उत्तर :
दो घटनाएँ निरपेक्ष है।
∴ P(A∪B) = P(A) × P(B)
0.12 = P(A) × 0.3
\(\frac{0.12}{0.3}\) = P(A)
∴ P(A)= 0.4
अब योग के नियम अनुसार
P(A∪B) = P(A) + P(B) – P(A∩B) = 0.4 + 0.3 – 0.12 = 0.58
मांगी गई संभावना = 0.58

प्रश्न 17.
यदि A = {x/1 < x < 3} B = (x/\(\frac {1}{2}\)) ≤ x < 2) हो, तो A∪B और A∩B ज्ञात कीजिए।
उत्तर :

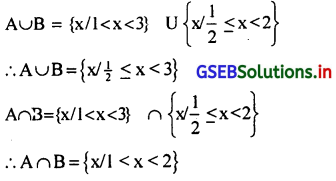
प्रश्न 18.
दो घटनाएँA और B में से कम से कम एक घटना घटने की संभावना \(\frac {1}{4}\) हो और घटनाA बने परंतु घटना B नघटे उसकी संभावना \(\frac {1}{5}\) हो, तो घटना Bघटने की संभावना का मान ज्ञात कीजिए।
उत्तर :
A और B में से कम से कम एक घटना घटेगी अर्थात् P(A∪B) = \(\frac {1}{4}\)
घटना A बने परंतु घटना B न घटे अर्थात् A – B बने ∴ P(A – B) = \(\frac {1}{5}\)
P(A∪B) = P(A) + P(B) – P(A∩B)
P(A – B) = P(A) – P(A∩B)
P(A∪B)= P(B) + P(A) – P(A∩B)
∴ P(A∪B) = P(B) + P(A – B)
\(\frac {1}{4}\) = P(B) + \(\frac {1}{5}\)
\(\frac{1}{4}-\frac{1}{5}\) = P(B)
∴ P(B) = \(\frac{5-4}{20}=\frac{1}{20}\)
मांगी गई संभावना = \(\frac {1}{20}\)

प्रश्न 19.
घटनाएँ A और B के लिए P(B) = \(\frac {3}{5}\) और P(A’∩B) = \(\frac {1}{2}\) हो, तो P(A/B) ज्ञात कीजिए।
उत्तर :

प्रश्न 20.
10 व्यक्तियों के समूह में 6 व्यक्तियों के पास पासपोर्ट है। इस समूह में से 3 व्यक्तियों का याद्दच्छिक रूप से चयन किया जाता है, तो उसमें
(1) तीनों व्यक्ति के पास पासपोर्ट हो।
(2) दो व्यक्ति के पास पासपोर्ट न हो, उसकी संभावना ज्ञात कीजिए।
उत्तर :
10 व्यक्तियों में से 3 व्यक्ति चयन करने का निदर्श अवकाश n = ¹⁰C₃ = \(\frac{10 \times 9 \times 8}{3 \times 2 \times 1}\) = 120

(1) तीनों व्यक्ति के पास पासपोर्ट हो उसे घटना A कहे तो A के सानुकूल परिणाम m = ⁶C₃ = \(\frac{6 \times 5 \times 4}{3 \times 2 \times 1}\) m = 20
∴ P(A) = \(\frac{m}{n}=\frac{20}{120}=\frac{1}{6}\)
मांगी गई संभावना = \(\frac{1}{6}\)

(2) दो व्यक्ति के पास पासपोर्ट न हो उसे घटना B कहे तो B के लिए सानुकूल परिणाम m = ⁴C₂ × ⁶C₁ = \(\frac{4 \times 3}{2 \times 1}\) × 6 = 6 × 6 = 36 m = 36
∴ P(B) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{36}{120}=\frac{3}{10}=\frac{3}{10}\)
मांगी गई संभावना = \(\frac{3}{10}\)

प्रश्न 21.
किसी वर्ष के बजेट में पुरुषों की आय के लिए आयकर मर्यादा में वृद्धि हो उसकी संभावना 0.66 और स्त्रियों की आय के लिए कर मर्यादा में वृद्धि होने की संभावना 0.72 है। पुरुषों और स्त्रियों की ऐसे दोनों की आय के लिए आयकर मर्यादा में वृद्धि हो उसकी संभावना 0.47 हो, तो उस वर्ष के बजट में
(1) पुरुषों और स्त्रियों दोनों में से सिर्फ एक की आय के लिए आयकर-मर्यादा में वृद्धि हो
(2) पुरुषों और स्त्रियों दोनों में से किसी की आय के लिए आयकर मर्यादा में वृद्धि न हो उसकी संभावना ज्ञात कीजिए।
उत्तर :
A = बजेट में पुरुषों की आय के लिए आयकर-मर्यादा में वृद्धि हो वह घटना ∴ P(A) = 0.66
B = बजेट में स्त्रियों की आय के लिए आयकर-मर्यादा में वृद्धि हो वह घटना ∴ P(B) = 0.72
A∩B = पुरुषों और स्त्रियों की दोनों की आय के लिए आयकर मर्यादा में वृद्धि हो वह घटना ∴ P(A∩B) = 0.47

(1) पुरुषो और स्त्रियों दो में से सिर्फ एक की आय के लिए आयकर-मर्यादा में वृद्धि हो वह घटना अर्थात् A घटे और B न घटे अथवा B घटे और
A न घटे
∴ अंतर घटना A – B अथवा B – A घटे
सिर्फ एक की आय के लिए आयकर मर्यादा में वृद्धि हो = P(A – B) + P(B – A)
P(A – B) = P(A) – P(A∩B) + P(B – A) = P(B) – P(A∩B) = 0.66 – 0.47 + 0.72 – 0.47 = 0.19 + 0.25 = 0.44
मांगी गई संभावना = 0.44

(2) पुरुष और स्त्रियों में से किसी की आय के लिए आयकर मर्यादा में वृद्धि न हो अर्थात् A’∩B’ बने P(A’∩B’) = 1 – P(A∪B) इसलिए
प्रथम P(A∪B) ज्ञात करेंगे योग के नियम के अनुसार
P(A∪B) = P(A) + P(B) – P(A∩B) = 0.66 + 0.72 – 0.47 = 1.38 – 0.47
∴ P(A∪B) = 0.91
अब P(A’∩B’) = 1 – P(A∪B) = 1 – 0.91
∴ P (A’∩B’) = 0.09
मांगी गई संभावना = 0.09

प्रश्न 22.
क्रूड ऑईल के मूल्य में वृद्धि होने के बाद पेट्रोल के मूल्य में वृद्धि हो ऐसा 80% किस्सा में बनता है और डिजल के मूल्य में वृद्धि हो ऐसा 77% किस्से में होता है।पेट्रोल और डीजल दोनों के मूल्य में वृद्धि हो ऐसा 68% किस्से में होता है। पेट्रोल का मूल्य में वृद्धि हुई है उसी शर्ताधीन डीजल के मूल्य में वृद्धि हो उसकी संभावना ज्ञात कीजिए।
उत्तर :
A = पेट्रोल के मूल्य में वृद्धि हो वह घटना ∴ P(A) = \(\frac{80}{100}\) = 0.80
B= डीजल के मूल्य में वृद्धि हो वह घटना ∴ P(B) = \(\frac{77}{100}\) = 0.77
A∩B = पेट्रोल और डीजल दोनों के मूल्य में वृद्धि हो वह घटना ∴ P(A∩B) = \(\frac{68}{100}\) = 0.68
पेट्रोल के मूल्य में वृद्धि हुई हो उसी शर्ताधीन डीजल का मूल्य में वृद्धि हो अर्थात् A बन चुकी है उसी शर्ताधीन B बने वह घटना B/A बने शर्ती संभावना के नियम अनुसार
P(B/A) = \(\frac{P(A \cap B)}{P(A)}=\frac{0.68}{0.80}=\frac{17}{20}\)
मांगी गई संभावना = \(\frac{17}{20}\)

प्रश्न 23.
मौसम विभागके पूर्वानुमान के अनुसार सप्ताहकेतीन दिन गुरुवार,शुक्रवार और शनिवार के दिन बारिश होने की संभावनाक्रमशः 0.8, 0.7 और 0.6 है।अगले सप्ताह में यह तीन दिनों में से कम से कम एक दिन बारिश होने की संभावना ज्ञात कीजिए।
(नोटः सप्ताह के तीन दिन गुरुवार, शुक्रवार और शनिवार के दिन बारिश गीरे उसकी घटनाएँ निरपेक्ष है।)
उत्तर :
A = गुरुवार को बारिश हो वह घटना ∴ P(A)= 0.8
B = शुक्रवार को बारिश हो वह घटना ∴ P(B)= 0.7
C = शनिवार को बारिश हो वह घटना ∴ P(C) = 0.6
तीनों घटनाए निरपेक्ष है इसलिए P(A∩B) = P(A) × P(B),P(A∩C) = P(A) × P(C), P(B∩C) = P(B) × P(C)ओर
P(A∩B∩C) = P(A) × P(B) × P(C) होगा।
अगला सप्ताह में तीन दिनों में से कम से कम एक दिन बारिश होने की घटना अर्थात् A∪B∪C बने। तीनों घटनाएँ निरपेक्ष है इसलिए योग का नियम निम्नानुसार बनेगा।

P(A∪B∪C)= P(A) + P(B) + P(C) – P(A) × P(B) – P(A) × P(C) – P(B) × P(C) + P(A) × P(B) × P(C)
= 0.8 + 0.7 + 0.6 – (0.8 × 0.7) – (0.8 × 0.6) – (0.7 × 0.6) + (0.8 × 0.7 × 0.6)
= 2.1 – 0.56 – 0.48 – 0.42 + 0.336 = 0.976
मांगी गई संभावना = 0.976

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.

डिजिटल स्टोर A में LED T.V.और 4LCDT.V. तथा डिजिटल स्टोर B में 5 LED T.V. और 3 LCD T.V. डिस्प्ले में रखा गया है। दो में से एक स्टोर का यादृच्छिक रीति से चुनाव करके उसमें से एक T.V. का चुनाव किया जाता हैं, तो वे LCD T.V. होने
की संभावना ज्ञात कीजिए।
उत्तर :
डिजिटल स्टोर A और B में से एक स्टोर का चयन किया जाता है।
A₁ = डिजिटल स्टोर A चयन हो ऐसी घटना ∴ P(A₁)= 1/2
B₁ = डिजिटल स्टोर B चयन हो ऐसी घटना ∴ P(B₁) = 1/2

डिजिटल स्टोर A : डिजिटल स्टोर A में 6 LED T.V. और 4 LCD T.V. है। कुल 10 T.V. में से एक T.V. का चयन के कुल परिणाम n = ¹⁰C₁ = 10, L₁ = T.V. LCD चयन हो वह घटना
∴ घटना L₁ के सानुकूल परिणाम m = ⁴C₁ = 4 m = 4 P(L₁) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{4}{10}\)

डिजिटल स्टोर B: डिजिटल स्टोर B में 5 LEDT.V. और 3 LCDT.V. है। कुल 8T.V. है उसमें से एक T.V. का चयन के कुल परिणाम n = ⁸C₁ = 8, L₂ = T.V. LCD चयन हो वह घटना
∴ घटना L₂ के सानुकूल परिणाम m = ³C₁ = 3, m = 3 P(L₂) = \(\frac{m}{n}=\frac{3}{8}\)
चुना गया T.V. LCD हो इसकी संभावना

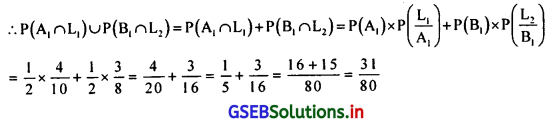
मांगी गई संभावना = \(\frac{31}{80}\)

प्रश्न 2.
1 से 100 तक की प्राकृतिक संख्याओं में से एक संख्या यादृच्छिक रीति से चयन की जाती है। चयन की गई संख्या एक अंक की हो अथवा पूर्ण वर्ग हो उस घटना की संभावना ज्ञात कीजिए।
उत्तर :
एक अंक की हो उसे घटना A कहे तो A के लिए सानुकूल परिणाम A = {1, 2, 3, 4, 5, 6, 7, 8, 9} = 9 ∴ m = 9
100 में से एक संख्या चयन करने का निदर्श अवकाश n = ¹⁰⁰C₁ = 100 ∴ n = 100
∴ P(A) = \(\frac{m}{n}=\frac{9}{100}\)
पूर्णवर्ग हो उसे घटना B कहे तो B के लिए सानुकूल परिणाम B = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100} m= 10
∴ P(B) = \(\frac{m}{n}=\frac{10}{100}\)
एक अंक की और पूर्णवर्ग हो उसे घटना A∩B कहे तो A∩B के सानुकूल परिणाम A∩B = {1, 4, 9} m = 3
∴ P(A∩B)= \(\frac{m}{n}=\frac{3}{100}\)
एक अंक की अथवा पूर्णवर्ग हो अर्थात् A∪B बने
योग के नियम अनुसार
P(A∪B) = P(A) + P(B) – P(A∩B) = \(\frac{9}{100}+\frac{10}{100}-\frac{3}{100}\) = \(\frac{9+10-3}{100}=\frac{16}{100}=\frac{4}{25}\)
मांगी गई संभावना = \(\frac{4}{25}\)

प्रश्न 3.
एक संतुलित सिक्के को तीन बार उछाला जाता है। यदि प्रथम दो प्रयत्नों में सिक्केपर काँटा मिला हो तो तीनों प्रयत्नों में सिक्केपर काँटा
मिले उसकी संभावना ज्ञात कीजिए।
उत्तर :
एक संतुलित सिक्के को तीन बार उछालने की निदर्श अवकाश के परिणाम n = 2³ = 8
U = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
प्रथम दो प्रयत्न में सिक्के पर काँटा मिले उसे घटना A कहे तो A के सानुकूल परिणाम A = {TTH, TTT} m = 2
∴ P(A) = \(\frac{m}{n}=\frac{2}{8}=\frac{1}{4}\)
तीनों प्रयत्न में काँटा मिले उसे घटना B कहे तो B के सानुकूल परिणाम B = {TTT} m = 1
∴ P(B) = \(\frac{m}{n}=\frac{1}{8}\)
A∩B = प्रथम दो प्रयल में काँटा और तीनों प्रयत्न में काँटा मिले वह घटना इसलिए A∩B के सानुकूल परिणाम A∩B = {TIT} m = 1
∴ P(A∩B) = \(\frac{m}{n}=\frac{1}{8}\)
प्रथम दो प्रयत्नों में काँटा मिला हो तो तीनों प्रयत्न में काँटा मिले अर्थात् A बन चुकी है उसी शर्ताधीन B बने अर्थात् B/A बने

मांगी गई संभावना = \(\frac{1}{2}\)

प्रश्न 4.
घटनाएँ A, B, C निरपेक्ष घटनाएं है और उसके लिए P(A) = P(B) = P(C) = P हो, तो P(A∪B∪C) का मूल्य P के स्वरूप में
प्राप्त कीजिए।
उत्तर :
A, B और C निरपेक्ष घटनाएँ है। इसलिए
P(A∩B) = P(A) × P(B), P(A∩C) = P(A) × P(C), P(B∩C) = P(B) × P(C), p(A∩B∩C) = R(A) × P(B) × P(C)
योग के नियम के अनुसार
P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(A∩C) – P(B∩C) + P(A∩B∩C)
= P(A) + P(B) + P(C) – [P(A) × P(B)] – [P(A) × P(C)]- [P(B) × P(C)] + [P(A) × P(B) × P(C)]
अब P(A)= P(B) = P(C) =P है
∴ P(A) = P, P(B) = P, P(C) = P सूत्र में रखने पर
P(A∪B∪C) = P + P + P – (P × P) – (P × P) – (P × P) + (P × P × P) = 3P – P² – P² – P² + P³ = 3P – 3P² + P³ = P(3 – 3P + P²)
मांगी गई संभावना = P(3 – 3P + P²)

प्रश्न 5.
एक राज्य के सरकारी नोकरी करते वर्ग-3 और वर्ग-4 के कर्मचारीओं में से चयन किये गये 6000 कर्मचारीओं के न्यादर्श जाति अनुसार सूचना निम्नानुसार सारणी में दर्शाया गया है।

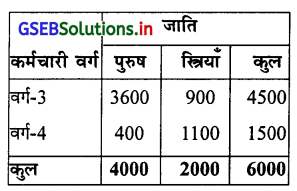
इस राज्य के सरकारी नोकरी करते वर्ग-3 और वर्ग-4 के सभी कर्मचारियों में से एक कर्मचारी को यादृच्छिक रीति से चयन किया जाता है।
(1) चयन हुए कर्मचारी पुरुष हो, तो वह वर्ग-3 का हो उसकी संभावना ज्ञात कीजिए।
(2) चयन हुए कर्मचारी वर्ग-3 का हो ऐसा दिया हो, तो वह पुरुष होने की संभावना ज्ञात कीजिए।
उत्तर :
यहाँ न्यादर्श में चयन हुए इकाई की संख्या 6000 है।
घटना A = पुरुष हो वह घटना

घटना B = चयन हुआ कर्मचारी वर्ग – 3 का हो वह घटना

घटना A∩B = पुरुष हो और वर्ग-3 का कर्मचारी हो

(1) चयन हुआ कर्मचारी पुरुष हो तो वह वर्ग-3 का कर्मचारी हो अर्थात् A बन चुकी है उसी शर्ताधीन B बने = B/A
शर्ती संभावना की परिभाषा के अनुसार घटना B/A की संभावना

मांगी गई संभावना = \(\frac {9}{10}\)

(2) चयन हुआ कर्मचारी वर्ग-3 का हो तो वह पुरुष हो अर्थात् घटना B बन चुकी है उसी शर्ताधीन घटना A बने = A/B
शर्ती संभावना की परिभाषा के अनुसार घटना A/B की संभावना

मांगी गई संभावना = \(\frac {4}{5}\)