GSEB Solutions Class 12 Statistics Part 2 Chapter 2 याद्दच्छिक चल और असतत संभावना-वितरण Ex 2

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 2 याद्दच्छिक चल और असतत संभावना-वितरण Ex 2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 2 याद्दच्छिक चल और असतत संभावना-वितरण Ex 2

विभाग – A

निम्न दिये गए विकल्पों में से सही विकल्प चुन करके लिखिए।

प्रश्न 1.
निम्न में से कौन-सा चल असतत चल का उदाहरण है?
(a) विद्यार्थियों की ऊँचाई
(b) विद्यार्थियों का वजन
(c) विद्यार्थियों का रक्तचाप
(d) विद्यार्थियों का जन्म वर्ष
उत्तर :
(d) विद्यार्थियों का जन्म वर्ष

प्रश्न 2.
निम्न में से कौन-सा चल सतत चल का उदाहरण है?
(a) किसी एक स्थान पर होनेवाली दुर्घटनाओं की संख्या
(b) वर्ष दौरान बारिश हुई हो ऐसे दिनों की संख्या
(c) दिन के दौरान महत्तम तापमान
(d) परिवार में बालकों की संख्या
उत्तर :
(c) दिन के दौरान महत्तम तापमान

प्रश्न 3.
यदि यादृच्छिक चल X यह -1, 0 और 1 का मूल्य धारण करे उसकी संभावना क्रमशः 1/5, k तथा 1/3 है। जहाँ 0 < k < 1 और x यदिइन मूल्य के अलावा अन्य मूल्यों को धारण न करता हो, तो E(x) का मूल्य क्या होगा?
(a) \(\frac{2}{5}\)
(b) \(\frac{3}{5}\)
(c) \(\frac{2}{15}\)
(d) \(\frac{3}{15}\)
उत्तर :
(c) \(\frac{2}{15}\)

प्रश्न 4.
एक यादृच्छिक चल सिर्फ -2,0 और 2 के मूल्यों को धारण करता है जिसकी संभावना क्रमशः1/5,3/5 और k है 0 < k < 1 हो, तोk का मूल्य क्या होगा?
(a) \(\frac{1}{5}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{2}{5}\)
(d) \(\frac{3}{5}\)
उत्तर :
(a) \(\frac{1}{5}\)

प्रश्न 5.
एकअसततसंभावना-वितरणकेलिए उसकामाध्यकामूल्य3 हैजबकि उसकाविचरण 7 है,तोवितरणकेलिए E(x²) क्या होगा?
(a) 10
(b) 4
(c) 40
(d) 16
उत्तर :
(d) 16

प्रश्न 6.
एक असतत चल X का संभावना-वितरण के लिए E(x) = 5 तथा E(x²) = 35 है, तो यह वितरण का विचरण क्या होगा?
(a) 40
(b) 30
(c) 20
(d) 10
उत्तर :
(d) 10

प्रश्न 7.
n = 10 प्राचलवाला धन विषम द्विपद वितरण के लिए निम्न में से दिए गए मूल्यों में से कौन-सा मूल्य माध्य का होगा?
(a) 5
(b) 3
(c) 9
(d) 7
उत्तर :
(b) 3

प्रश्न 8.
n = 4 तथा P = \(\frac {1}{2}\) प्राचलवाला द्विपद वितरण के लिए P(x) का मूल्य x की कौन-सी किंमत के लिए महत्तम बनेगें ?
(a) 0
(b) 2
(c) 3
(d) 4
उत्तर :
(b) 2

प्रश्न 9.
एक द्विपद वितरण का माध्य 5 तथा विचरण \(\frac {10}{7}\) है, तो यह वितरण कैसा बनेगा?
(a) धन विषम
(b) ऋण विषम
(c) संमित
(d) वितरण के बारे में कुछ नहि कहा जा सकता
उत्तर :
(a) धन विषम

प्रश्न 10.
n और P प्राचलवाला द्विपद वितरण के लिए एक भी सफलता न मिले तो उस घटना की संभावना के लिए सूत्र निम्न में से कौन-सा
होगा?
(a) ⁿC₀pⁿq⁰
(b) ⁿC₀p⁰qⁿ
(c) ⁿC₀pqⁿ
(d) ⁿC₀pⁿq
उत्तर :
(b) ⁿC₀p⁰qⁿ

विभाग – B

निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए।

प्रश्न 1.
असतत याद्दच्छिक चल की परिभाषा दीजिए।
उत्तर :
याद्दच्छिक चल X जो वास्तविक संख्या समुच्चय R में या उसके उपसमुच्चय में किया जा सके उतनी ही किंमतों को धारण कर सकता हो, तो ऐसे चर x को असतत (खंडित) याद्दच्छिक चर कहते है।

प्रश्न 2.
सतत यादृच्छिक चर की परिभाषा दीजिए।
उत्तर :
यदि याद्दच्छिक चर X समुच्चय R में अथवा उसका उपसमुच्चय हो ऐसे अन्तराल के किसी भी मूल्य को धारण करने में समर्थ हो, तो उस चर x को सतत याद्दच्छिक चर कहते है।

प्रश्न 3.
असतत संभावना-वितरण की परिभाषा दीजिए।
उत्तर :
यदि x यह धारित मूल्य x₁ की संभावना P(X = x₁) = P(x₁) हो जहाँ i = 1, 2,….n के लिए P(x₁) ≥ 0 होगा तथा
\(\sum_{i=1}^n P\left(x_1\right)\) = P(x₁) + P(x₂) +…….+ P(x_n) = होगा इन वास्तविक मूल्यों के समुच्चय {p(x₁), p(x₂)……. P(x_n)} को असतत याद्दच्छिक चर का संभावना-वितरण कहेंगे।

प्रश्न 4.
असतत चर का माध्य ज्ञात करने का सूत्र लिखिए।
उत्तर :
असतत यादृच्छिक चर x का माध्य को μ अथवा E(x) से दर्शाया जाता है।
सूत्र → μ = Σ(x) = Σx₁ P(x₁) उसे असतत चल x की अपेक्षित किंमत भी कहते है।

प्रश्न 5.
असतत चल का विचरण ज्ञात करने का सूत्र बताइए।
उत्तर :
असतत संभावना वितरण का विचरण = δ²
= V(H) = Σ(x)² = (Σ(x))² जहाँ = Σ(x²) = Σx².P(x)

प्रश्न 6.
एक संमित द्विपद वितरण का माध्य 7 है। उसका प्राचलn का मूल्य बताइए।
उत्तर :
आवृत्ति-वितरण संमित है इसलिए P = \(\frac {1}{2}\) और q = \(\frac {1}{2}\) माध्य = 7 दिया है ∴ माध्य = np = 7
अब माध्य np में P = \(\frac {1}{2}\) रखने पर 7 = n × \(\frac {1}{2}\) ∴ 7 × \(\frac {2}{1}\) = n ∴ n = 14

प्रश्न 7.
एक द्विपद वितरण का प्राचल क्रमशः 10 तथा \(\frac{2}{5}\) है, तो उसका विचरण की गणना कीजिए।
उत्तर :
द्विपद वितरण के प्राचल क्रमशः 10 तथा \(\frac{2}{5}\) है इसलिए
n = 10, P = \(\frac{2}{5}\) ∴ q = 1 – P = 1 – \(\frac{2}{5}=\frac{5-2}{5}=\frac{3}{5}\) ∴ q = \(\frac{3}{5}\)
विचरण = npq में p, q, n का मान रखने पर
10 × \(\frac{2}{5} \times \frac{3}{5}=\frac{60}{25}=\frac{12}{5}\) विचरण \(\frac{12}{5}\) अथवा 2.4

प्रश्न 8.
बर्नोली प्रयत्नों में सफलता और निष्फलता की संभावना के बीच का संबंध बताइए।
उत्तर :
सफलता को P और निष्फलता को माना जाता है।
∴ P + q = 1 P = 1 – q अथवा q = 1 – P होगा

प्रश्न 9.
द्विपद वितरण का माध्य और विचरण के बीच का संबंध बताइए।
उत्तर :
द्विपद वितरण का माध्य विचरण से अधिक होता है अर्थात् माध्य > विचरण np > npq

प्रश्न 10.
एक द्विपद वितरण के निष्फलता की संभावना 0.6 है तथा इसमें कुल प्रयत्नों की संख्या 5 है, तो यह वितरण के लिए सफलता की
संभावना ज्ञात कीजिए।
उत्तर :
निष्फलता की संभावना को माना जाय तो q = 0.6
∴ सफलता की संभावना P = 1 – q = 1 – 0.6 = 0.4 ∴ P = 0.4

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
चल x का संभावना-वितरण निम्नानुसार है।

तो अचलांक C का मूल्य निश्चित कीजिए।
उत्तर :
संभावना वितरण को परिभाषा अनुसार ΣP(x) = 1
∴ P(2) + P(3) + P(4) + P(5) = 1
0.2 + 0.3 + 4C + C = 1
∴ 5C = 1 – 0.5, 5C = 0.5
∴ C = \(\frac{0.5}{5}\)
∴ C = 0.1

प्रश्न 2.
असतत संभावना-वितरण के लिए वितरण का माध्य की गणना कीजिए।
उत्तर :
वितरण का माध्य का सूत्र μ = Σ(x) = Σx₁(Px₁)

प्रश्न 3.
एक यादृच्छिक चल का संभावना-वितरण निम्नानुसार है। P(x) = \(\frac{x+3}{10}\), x = -2, 1 ,2 तो उस पर से E(x²) की गणना कीजिए।
उत्तर :
विचरण ज्ञात करने का सूत्र E(x²) Σ(x²) = Σx².P(x)
प्रथम P(x) = \(\frac{x+3}{10}\) में x = -2, 1, 2 रखने पर

E(x²) = 2.8

प्रश्न 4.
एक संमित द्विपद वितरण के लिए यदि n = 4 हो, तो P(4) ज्ञात कीजिए।
उत्तर :
संमित द्विपद वितरण में P = \(\frac {1}{2}\) और q = \(\frac {1}{2}\) होता है। n = 4 दिया है। P(4) ज्ञात करना है इसलिए x = 4 रखेंगे।
P(x) = ⁿC_xP^xq^{n – x} x = 0, 1, …..n सूत्र में n, p, q, x का मान रखने पर
P(4)= ⁴C₄ (\(\frac {1}{2}\))⁴ (\(\frac {1}{2}\))^{4 – 4} = 1 × \(\frac {1}{16}\) × 1 = \(\frac {1}{16}\) ∴ P(4) = \(\frac {1}{16}\)

प्रश्न 5.
बर्नोली प्रयत्नों की परिभाषा दीजिए।
उत्तर :
यदि द्विविध विकल्प विशेषता धारित यादृच्छिक प्रयोग के दो संभवित परिणाम सफलता (S) और निष्फलता (F) हो तथा इस प्रयोग का n बार पुनरावर्तन हो और प्रत्येक प्रयत्न में सफलता की संभावना P(0 < P < 1) अचल रहे तो ऐसे प्रयत्नों को बर्नोली प्रयत्न कहेंगे।

प्रश्न 6.
एक द्विपद वितरण के लिए यदि सफलता की संभावना यदि निष्फलता की संभावना से दो गुनी हो और n = 4 हो, तो वितरण का विचरण क्या होगा?
उत्तर :
सफलता की संभावना यह निष्फलता की संभावना से दो गुनी है। सफलता को P और निष्फलता को q मानने पर P = 2q होगा।
P + q = 1 में P=2q रखने पर 2q + q = 1
3q = 1 ∴ P = 1 – q = 1 – \(\frac {1}{3}\)
∴ q = \(\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\)
P = \(\frac {2}{3}\)n = 4 दिया है
∴ विचरण = npq = 4 × \(\frac {2}{3}\) × \(\frac {1}{3}\) विचरण = \(\frac {8}{9}\)

प्रश्न 7.
n = 8 तथा निष्फलता की संभावना 2/3 हो ऐसे द्विपद वितरण का प्रमाप विचलन ज्ञात कीजिए।
उत्तर :
निष्फलता की संभावना को मानने पर
q = \(\frac {2}{3}\) ∴ P + q = 1 p = 1 – q = 1 – \(\frac{2}{3}=\frac{1}{3}\) ∴ P = \(\frac {1}{3}\) n = 8 दिया है।
इसलिए प्रमाप विचलन = \(\sqrt{\mathrm{npq}}=\sqrt{8 \times \frac{1}{3} \times \frac{2}{3}}=\sqrt{\frac{16}{9}}\)
∴ प्रमाप विचलन = \(\frac {4}{3}\)

प्रश्न 8.
एक द्विपद वितरण का माध्य = 4 और विचरण =2 हो, तो विचरण के प्राचल ज्ञात कीजिए।
उत्तर :
माध्य = np = 4 और विचरण npq = 2 दिया है।
∴ q = \(\frac{n p q}{n p}=\frac{2}{4}\)
q = \(\frac {1}{2}\) ∴ P = 1 – q = 1 – \(\frac {1}{2}\) = \(\frac {1}{2}\) P = \(\frac {1}{2}\)
अब माध्य = np = 4
n × \(\frac {1}{2}\) = 4
n = \(\frac{4 \times 2}{1}\) ∴ n = 8
प्राचल n = 8 और P = \(\frac {1}{2}\)

प्रश्न 9.
एक द्विपद वितरण के लिए n=10 और q – p= 0.6 है, तो वितरण का माध्य ज्ञात कीजिए।
उत्तर :
यहाँ n = 10 और q – p = 0.6 दिया है।
q + p = 1 ∴ q = 0.6 + p
0.6 + p + p = 1
∴ 2p = 1 – 0.6 वितरण का माध्य = np = 10 × 0.2
p = \(\frac{0.4}{2}\) माध्य = 2
∴ p = 0.2
q = 1 – p
= 1 – 0.2
q = 0.8

प्रश्न 10.
एक द्विपद वितरण के लिए प्रमाप विचलन 0.8 है, तथा निष्फलता की संभावना \(\frac {2}{3}\) है, तो वितरण का माध्य ज्ञात कीजिए।
उत्तर :
द्विपद वितरण का प्रमाप विचलन 0.8 है।
∴ \(\sqrt{\mathrm{npq}}\) = 0.8
निष्फलता की संभावना के \(\frac {2}{3}\) है
∴ q = \(\frac {2}{3}\)
∴ P = 1 – q
= 1 – \(\frac {2}{3}\) P = \(\frac {1}{3}\)
\(\sqrt{\mathrm{npq}}\) = 0.8 में P = \(\frac {1}{3}\) और q = \(\frac {2}{3}\) रखने पर
\(\sqrt{n \times \frac{1}{3} \times \frac{2}{3}}\) = 0.8 माध्य = np = 2.88 × \(\frac {1}{3}\) = 0.96
n × \(\frac {2}{9}\) = (0.8)² माध्य = 0.96
n × \(\frac {2}{9}\) = 0.64
n = \(\frac{0.64 \times 9}{2}\)
n = 2.88

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए।

प्रश्न 1.
एक यादृच्छिक चल X का संभावना-वितरण निम्नानुसार है : तो अचलांक k का मूल्य ज्ञात कीजिए तथा चल x यह युग्म मूल्य धारण करे तो संभावना ज्ञात कीजिए।
उत्तर :
P(x) = k(x – 1) जहाँ x = 2 रखने पर
P(2) = k(2 – 1)
P(2) = k
P(x) = k(x – 1) जहाँ x = 3 रखने पर
P(3) = k(3 – 1)
P(3) = 2k
P(4) = k x = 4
रखने पर k(6 – x) में x = 5 रखने पर
P(5) = k(6 – 5) P(5) = k

संभावना-वितरण की परिभाषा अनुसार ΣP(x) = 1 P(2) + P(3) + P(4) + P(5) = 1 k + 2k + k + k = 1 5k = 1 ∴ k = \(\frac {1}{5}\)
अचलांक k = \(\frac {1}{5}\)
x यह युग्म संख्या धारण करे अर्थात् x = 2, 4 हो उसकी संभावना = P(2) + P(4) = k + k = 2k, k = \(\frac {1}{5}\) रखने पर
= 2 × \(\frac {1}{5}\) = \(\frac {2}{5}\), x यह युग्म संख्या धारण करने की संभावना \(\frac {2}{5}\)

प्रश्न 2.
एक यादृच्छिक चल x का संभावना-वितरण निम्नानुसार है: P(x) = C(x² + x), x = -2, 1, 2 हो,तो C का मूल्य ज्ञात कीजिए तथा P(2) = 3P(-2) है ऐसा सिद्ध कीजिए।
उत्तर :
असतत संभावना-वितरण की परिभाषा अनुसार ΣP(x) = 1
P(x) = C(x² + x) में x = -2, 1, 2 रखने पर
P(-2) = C(-2)² + (-2) = C (4 – 2)
P(2) = C(2² + 2) = C(4 + 2) = 6C
P(-2) = 2C
P(1) = C(1² + 1) = C(1 + 1)
P(1) = 2C
P(-2) + P(1) + P(2) = 1
2C + 2C + 6C = 1
10C = 1
∴ C = \(\frac {1}{10}\)
P(2) =3P(-2) है ऐसा सिद्ध कीजिए P(2) = 6C और P(-2) = 2C रखने पर
6C = 3(2C)
6C = 6C ∴ P(2) = 3P(-2) समान होता है।

प्रश्न 3.
एक यादृच्छिक चलx का वितरण P(x) = k.⁵P_x x = 0, 1, 2, 3, 4, 5 है,तो अचलांक k ज्ञात कीजिए तथा वितरण का माध्य ज्ञात कीजिए।
उत्तर :
ΣP(x) = 1
P(x) = k.⁵P_x में x = 0, 1, 2, 3, 4, 5 रखने पर
P(0) = k.⁵P₀
P(0)= k × 1
P(0)= k
P(1)= k.⁵P₁ = k.5
P(1) = 5k
P(2) = k.⁵P₂ = k × 5 × 4
P(2) = 20k
P(3) = k.⁵P₃ = k × 5 × 4 × 3
P(3) = 60k
P(4) = k × ⁵P₂ = k × 5 × 4 × 3 × 2
P(4) = 120k
P(5) = k × ⁵P₂ = k × 5 × 4 × 3 × 2 × 1 = 120k

P(0) + P(1) + P(2) + P(3) + P(4) + P(5) = 1
k + 5k + 20k + 60k + 120k + 120k = 1
326k = 1
∴ k = \(\frac{1}{326}\) अचलांक k = \(\frac{1}{326}\)
संभावना-वितरण का माध्य का सूत्र E(x) = Σx_i × P(x_i) = 0 × k + 1 × 5k + 2 × 20k + 3 × 60k +4 × 120k + 5 × 120k
= 5k + 40k + 180k + 480k + 600k = 1305k
k = \(\frac{1}{326}\) रखने पर
= 1305 × \(\frac{1}{326}\)
माध्य = \([latex]\frac{1305}{326}\)[/latex]

प्रश्न 4.
असतत संभावना-वितरण अर्थात् क्या ? उसके गुणधर्म बताइए।
उत्तर :
मानाकि x : U → R एक याद्दच्छिक चल है, जो R के उपसमुच्चय (x₁,x₂…….x_n) में से ही किसी एक मूल्य धारित कर सकते है। मानाकि
x धारित की गई किंमत x_i की संभावना P(x = x_i) = P(x_i) है। यदि P(x_i) > 0, i = 1, 2….n और ΣP(x_i) = 1 हो, तो वास्तविक समुच्चय {x₁,x₂…..x_n} और {P(x₁), P(x₂)…P(x_n)} को याद्दच्छिक चल x का असतत संभावना-वितरण कहते है।

असतत संभावना-वितरण के गुणधर्म: ।

1. यदि x एक याद्दच्छिक चल हो, तो परिभाषा अनुसार x वास्तविक संख्या समुच्चय R किसी भी मूल्य को धारण कर सकता है।
2. दो अन्तराल के कुछ ही मूल्य को धारण कर सकता है।

प्रश्न 5.
द्विपद वितरण के गुणधर्म बताइए।
उत्तर :

1. द्विपद वितरण एक असतत वितरण है।
2. इस वितरण के प्राचल n और p है।
3. इस वितरण का माध्य np है जो n बर्नोली प्रयत्नों में प्राप्त होनेवाली औसत संख्या का निर्देश करती है।
4. इस वितरण का विचरण npq और प्रमाप विचलन = \(\sqrt{n p q}\) है।
5. द्विपद वितरण में हमेशा माध्य यह विचरण से बड़ा होता है तथा
   = \(\frac{n p q}{n p}\) = q निष्फलता की संभावना है।
6. n के किसी भी मूल्य के लिए P < \(\frac {1}{2}\) हो, तो इस वितरण की विषमता धन होगी।
7. n के किसी भी मूल्य के लिए P > \(\frac {1}{2}\) हो, तो यह वितरण की विषमता ऋण होगी।
8. n के किसी भी मूल्य के लिए P = \(\frac {1}{2}\) हो, तो यह वितरण संमित है ऐसा कहेंगे और उसकी विषमता शून्य (0) होगी।

प्रश्न 6.
निशान लक्षभेदन करने के एक खेल में रमेश निशान का भेदन करने में निष्फल हो उसकी संभावना \(\frac {2}{5}\) है। यदि उसे निशाना लक्ष भेदन करने के लिए 3 प्रयत्न दिया जाय तो वह2 प्रयत्नों में लक्षभेदन में सफल हो जाय उसकी संभावना ज्ञात कीजिए और वितरण का
माध्य ज्ञात कीजिए।
उत्तर :
सफलता की संभावना ज्ञात करना है इसलिए P = \(\frac {3}{5}\) और q = \(\frac {2}{5}\) होगा। n = 3 और x = 2
असतत चल का द्विपद वितरण के अनुसार
P(x) = ⁿC_xp^xq^{n – x} x = 0, 1, 2…n
n, p, q और x के मान रखने पर
P(2) = ³C₂(\(\frac {3}{5}\))² (\(\frac {2}{5}\))^{3 – 2} = 3 × \(\frac{9}{25} \times \frac{2}{5}=\frac{54}{125}\)
दो प्रयत्नों में सफल हो उसकी संभावना = \(\frac{54}{125}\) माध्य = np = 3 × \(\frac {3}{5}\) माध्य = \(\frac {9}{5}\)

प्रश्न 7.
एक व्यक्ति को धन पूर्णांक 1 से 7 में से कोई एक संख्या चयन करने को कहा जाता है।यदि उसके द्वारा चयन किया गया अंक विषम संख्या हो तो उसे इनाम के पात्र माना जाता है। यदि इस व्यक्ति को 5 प्रयत्नों दिया जाय तो, वह सिर्फ एक प्रयत्न में ईनाम के पात्र बने उस घटना की संभावना ज्ञात कीजिए।
उत्तरः
धन पूर्णांक 1, 2, 3, 4, 5, 6, 7 में विषम संख्या 1, 3, 5, 7 है। उसे सफलता कहे तो P = \(\frac {4}{7}\) और q = 1 – P = 1 – \(\frac {4}{7}\) = \(\frac {3}{7}\) ∴ q = \(\frac {3}{7}\)
5 प्रयत्न दिया जाता है। ∴ n = 5
एक बार इनाम के पात्र बने अर्थात् x = 1
द्विपद वितरण का संभावना सूत्र के अनुसार
P(x) = ⁿC_xp^xq^{n – x} x = 1, 2, 3…n में n = 5, x = 1, P = \(\frac {4}{7}\) q = \(\frac {3}{7}\) रखने पर
P(1) = ⁵C (\(\frac {4}{7}\))¹(\(\frac {3}{7}\))^{5 – 1} = 5 × \(\frac{4}{7} \times \frac{81}{2401}=\frac{1620}{16807}\)
सिर्फ एक प्रयत्न में इनाम के पात्र बने उसकी संभावना = \(\frac{1620}{16807}\)

प्रश्न 8.
एक द्विपद वितरण का माध्य और विचरण क्रमशः 2 और 6/5 है, तो द्विपद वितरण के लिए P(1) और P(2) की गणना कीजिए।
उत्तरः
द्विपद वितरण का माध्य = 2 ∴ np = 2
द्विपद वितरण का विचरण = \(\frac{6}{5}\) ∴ npq = \(\frac{6}{5}\)
प्रथम प्राचल n और p ज्ञात करेंगे।

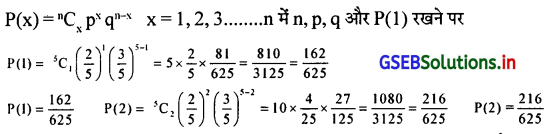
प्रश्न 9.
एक सेव के बॉक्स में 10% सेव सड़े हुए है। बॉक्स में से यादृच्छिक रीति से पूर्ति सहित चुने गए 6 सेव में से बराबर आधी संख्या के सेव सड़े हुए मिले उसकी संभावना ज्ञात कीजिए तथा सड़े हुए सेव की संख्या का विचरण ज्ञात कीजिए।
उत्तरः
सेव के बॉक्स में 10% सेव सड़े हुए है। उसे सफलता माना जाय तो
P = \(\frac{10}{100}=\frac{1}{10}\) ∴ P = \(\frac {1}{10}\)
∴ q = 1 – \(\frac{1}{10}=\frac{9}{10}\) ∴ q = \(\frac {9}{10}\)
n = 6 में आधे सेव सड़े हुए है इसलिए x = 3
द्विपद वितरण के संभावना सूत्र में रखने पर

विचरण = 0.54

विभाग – E

निम्न प्रश्नों को हल प्राप्त कीजिए।

प्रश्न 1.
किसी ए स्टोर्स में पटोप की मासिक मांग का संभावना-वितरण निम्नानुसार है।

लेपटोप की अपेक्षित मांग निश्चित कीजिए तथा मांग का विचरण ज्ञात कीजिए।
उत्तर :
लेपटोप की अपेक्षित मासिक मांग
E(x) = ΣxP(x) = 1 × 0.10 + 2 × 0.15 + 3 × 0.20 + 4 × 0.25 + 5 × 0.18 + 6 × 0.12
= 0.10 + 0.304 – 0.60 + 1.00 + 0.90 + 0.72 = 3.62
अपेक्षित मांग = 3.62
मांग का विचरण
अब E(x²) = Σx²P(x) = (1)² (0.10) + (2)²(0.15) + (3)² (0.20) + (4)²(0.25) + (5)² (0.18) + (6)² (0.12)
= 1 × 0.10 + 4 × 0.15 + 9 × 0.20 + 16 × 0.25 + 25 × 0.18 + 36 × 0.12
= 0.10 + 0.60 + 1.80 + 4.00 + 4.50 + 4.32 Σ(x²) = 15.32
x का विचरण =V(x)
E(x²) – (E(x))² = 15.32 – (3.62)² = 15.32 – 13.1044 = 2.2156
विचरण = 2.2156 = 2.22

प्रश्न 2.
दो संतुलित पासा को एक बार उछाला जाता है। इसमें से अंक ‘6’ उपर की तरह आये ऐसे पासा की संख्या का असतत संभावना वितरण प्राप्त कीजिए।
उत्तर :
दो संतुलित पासाओं को एक बार उछालने के निदर्श अवकाश U के घटक 36 प्राप्त होंगे प्रत्येक परिणाम में पूर्णांक 1, 2, 3, 4, 5 और 6 में से
किसी एक अंक प्राप्त होगा। U = {(i.j) = i,j = 1, 2, 3, 4, 5, 6}
उपर की अंक ‘6’ आये उसे x कहेंगे x = 0, 1, 2 होगा

(i) x = 0 हो उसकी संभावना P(x = 0) = P(6 का अंक न हो।)
{(11), (12), (13), (14), (15), (21), (22), (23), (24), (25), (31), (32), (33), (34), (35), (41), (42), (43), (44), (45), (51), (52), (53), (54), (55)} = 25
0 की संभावना = \(\frac{25}{36}\)

(ii) x = 1 हो उसकी संभावना P(x = 1)= P(सिर्फ 6 का अंक हो।)
{(1, 6), (2, 6), (36), (46), (56), (61), (62), (63), (64), (65) = 10
1 की संभावना = \(\frac{10}{30}\)

(iii) x = 2 हो उसकी संभावना P(x = 2) = P(दोनों पर 6 का अंक हो।)= {6, 6} = 1 ‘
P(2) = \(\frac{1}{36}\)
चल x का संभावना-वितरण निम्नानुसार सारणी स्वरूप में लिखेंगे।

प्रश्न 3.
50 वर्ष की उम्रवाली किसी भी व्यक्ति की एक वर्ष दौरान मृत्युहो उसकी संभावना 0.01 हो, तो ऐसी 5 व्यक्तियों के एक समूहमें से
(i) किसी भी व्यक्ति की एक वर्ष में मृत्युन हो।
(ii) कम से कम एक व्यक्ति की एक वर्ष दौरान मृत्यु हो उस घटना की संभावना ज्ञात कीजिए।
उत्तर :
एक वर्ष के दौरान अवसान हो जाय उसे सफलता मानने पर P = 0.01 इसलिए q = 1 – P = 1 – 0.01 = 0.99 ∴ q = 0.99 n = 5

(i) कोई भी व्यक्ति एक वर्ष में अवसान न हो x = 0 P(x) = ⁿC_x P^xq^{n – x}: x = 0, 1, 2…….n
n = 5, P = 0.01 q = 0.99 x = 0 रखने पर
P(0) = ⁵C₀ (0.01)⁰ (0.99)^{5 – 0} = 1 × 1 × 0.95099 P(0) = 0.9510
कोई भी व्यक्ति का एक वर्ष में अवसान नहीं होने की संभावना = 0.9510

(ii) कम से कम एक व्यक्ति का वर्ष में अवसान हो उस घटना की संभावना x = 1, 2, 3, 4, 5
मांगी गई संभावना = P(x ≥ 1) = P(1) + P(2) + P(3) + P(4) + P(5) = 1 – P(0) = 1 – 0.9510 = 0.049
कम से कम एक व्यक्ति का वर्ष में अवसान हो उसकी संभावना = 0.049

प्रश्न 4.
कक्षा 12 विज्ञान प्रवाह में अभ्यास करते विद्यार्थी ईन्जीनियरींग विद्याशाखा में प्रवेश प्राप्त करे उसकी संभावना 0.3 है। ऐसे विद्यार्थियों के न्यादर्श जाँच में 5 विद्यार्थी याद्दच्छिक रीति से चयन किये जाते है तो उनमें से ईन्जीनियरींग विद्याशाखा में प्रवेश लेनेवाले विद्यार्थियों की संख्या, इन्जीनियरींग विद्याशाखा में प्रवेश न लेनेवाले विद्यार्थियों की संख्या से अधिक हो उस घटना की संभावना ज्ञात कीजिए।
उत्तर :
विद्यार्थी इन्जीनियरींग विद्याशाखा में प्रवेश प्राप्त करे उसकी संभावना को सफलता मानने पर P = 0.3
q = 1 – P = 1 – 0.3 = 0.7 ∴ q = 0.7
5 विद्यार्थियों का याद्दच्छिक रीति से चयन किया जाता है। ∴ n = 5
इन्जीनियरींग में प्रवेश लेनेवाले विद्यार्थियों की संख्या इन्जीनियरींग में प्रवेश न लेनेवालों से अधिक हो उस घटना की संभावना
x = 3, 4, 5 रखने पर

P(x)= ⁿC_xp^xq^{n – x} x = 0, 1, 2….. n x = 3 रखने पर
P(3) = ⁵C₃ (0.3)³ (0.7)^{5 – 3} = 10 × 0.027 × 0.49 P(3) = 0.1323 x = 4 रखने पर
P(4) = ⁵C₄ (0.3)⁴ (0.7)^{5 – 4} = 5 × 0.0081 × 0.7 P(4) = 0.02835 x = 5 रखने पर
P(5) = ⁵C₅ (0.3)⁵ (0.7)^{5 – 5} = 1 × 0.00243 × 1 = 0.00243
अब = P(3) + P(4) + P(5) = 0.1323 + 0.02835 + 0.00243 = 0.16308
इन्जीनियरींग में प्रवेश लेनेवाले विद्यार्थियों की संख्या, इन्जीनियरींग विद्याशाखा में प्रवेश न लेनेवाले विद्यार्थियों से अधिक होने की संभावना
= 0.1631

प्रश्न 5.
एक पुल पर विमान में से फेंके गएबम पुल पर गिरे उसकी संभावना 1/5 है।पुल का विनाश करने हेतु दो बम आवश्यक है।यदि पुल पर 6 बम फेंका जाय तो पुल का विनाश होने की संभावना ज्ञात कीजिए।
उत्तर :
पुल पर विमान में से फेंके गए बम गिरे उसकी संभावना को सफलता गिने तो
P = \(\frac {1}{5}\) ∴ q = 1 – P = 1 – \(\frac {1}{5}\) = \(\frac {4}{5}\)
Q = \(\frac {4}{5}\)
6 बम फेंके गए है ∴ n = 6
पुल का विनाश करने हेतु दो बम आवश्यक है इसलिए पुल का विनाश के लिए x=2,3,4,5,6 बम गिरे तो विनाश होगा।
मांगी गई संभावना
P(x ≥ 2) = P(2) + P(3) + P(4) + P(5) + P(6) = 1 – [P(O) + P(1)]
= द्विपद संभावना का सूत्र P(x) = ⁿC_xp^xq^{n – x}x = 0, 1, 2….n

पुल का विनाश होने की संभावना = 0.3446

प्रश्न 6.
एक निश्चित परीक्षा में सामान्य रीति से 40% विद्यार्थी अनुत्तीर्ण होते है।6 विद्यार्थियों के एक समूहमें से कम से कम 4 विद्यार्थी एक परीक्षा में उत्तीर्ण हो उसकी संभावना ज्ञात कीजिए।
उत्तर :
उत्तीर्ण हो उसे सफलता गिनने पर उत्तीर्ण = P बनेगा अनुत्तीर्ण हो उसे निष्फलता q मानने पर q = \(\frac {40}{100}\)
= 0.4
∴ P = 1 – 0.4 = 0.6 ∴ P = 0.6 n = 6
कम से कम 4 विद्यार्थी एक परीक्षा में उत्तीर्ण हो अर्थात् P(x ≥ 4)
P(4) + P(5) + P(6) ज्ञात करेंगे।
द्विपद संभावना-वितरण का सूत्र P(x) = ⁿC_xp^xq^{n – x}
x = 0, 1, 2……n
P = 0.6, q = 0.4, n = 6,x = 4 रखने पर
P(4) = ⁶C₄ (0.6)⁴ (0.4)^{6 – 4} = 15 × 0.1296 × 0.16 = 0.3110
P(5) = ⁶C₅ x (0.6)⁵ (0.4)^{6 – 5} = 6 × 0.07776 × 0.4 = 0.1866
P(6) = ⁶C₆ (0.6)⁶ (0.4)^{6 – 6} = 1 × 0.0467 = 0.0467
अब P(4) + P(5) + P(6) = 0.3110 + 0.1866 + 0.0467 = 0.5443
कम से कम 4 विद्यार्थी उत्तीर्ण हो उसकी संभावना = 0.5443

प्रश्न 7.
एक बॉक्स में 3 लाल और 4 सफेद गेंद है। उसमें से चार गेंद पूर्ति सहित पसंद किया जाता है। यह पसंद किए गेंद में
(1) 2 लाल गेंद और 2 गेंद सफेद मिले तथा
(2) चारों गेंद सफेद मिले उसकी घटना की संभावना द्विपद वितरण का उपयोग करके प्राप्त कीजिए।
उत्तर
3 लाल और 4 सफेद गेंद में से 4 गेंद पूर्ति सहित चयन किया जाता है।
∴ P = \(\frac {4}{7}\) अब q = 1 – P
∴ q = 1 – \(\frac {4}{7}\) = \(\frac {3}{7}\)

(1) 2 लाल और 2 गेंद सफेद मिले n = 4, x = 2 P = \(\frac {4}{7}\) q = \(\frac {4}{7}\)
P(x) = ⁿC_xp^xq^{n – x}

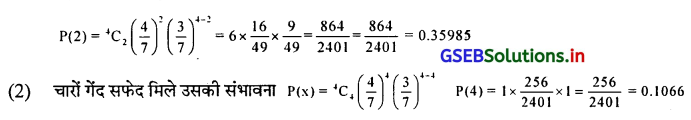
चारों सफेद गेंद की संभावना = 0.1066

विभाग – F

निम्न के हल निकालिए।

प्रश्न 1.
एक संदूक में एक दर्जन आम है। उसमें 3 आम सड़े हुए है।इस संदूक में से यादृच्छिक रूपसे पूर्ति सहित 3 आम का चयन किया जाता है।यदिx यहचयन की गई आम में सड़े हुई आमों की संख्या दर्शाता है, तो x का संभावना-वितरण प्राप्त कीजिए और उस पर से चयन किए आमों में सड़े आम की अपेक्षित किंमत तथा विचरण प्राप्त कीजिए।
उत्तरः
x = चयन की गई आम अच्छी हो उसकी संख्या दर्शाता है तो संभावना सूत्र अनुसार
(i) x = 0 आम सड़ी हुई हो उसकी संभावना = P(x = 0) = 0 सड़ी हुई आम हो

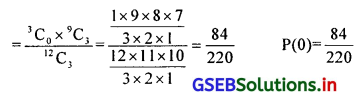
(ii) x = 1 आम सड़ी हुई हो उसकी संभावना P(x = 1) = 1 सड़ी हुई आम हो

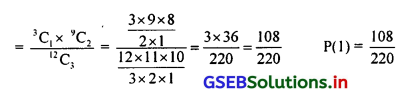
(iii) x = 2 आम सड़े हुए हो उसकी संभावना P(x = 2) = 2 आम सड़े हुए हो

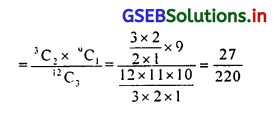
(iv) x = 3 आम सड़े हुए हो उसकी संभावना P(x = 3) = 3 आम सड़े हुए हो

प्रश्न 2.
कक्षा 10वीं में अभ्यारा करते विद्यार्थियों की समष्टि में 50% विद्यार्थी चोकलेट खाने की आदत रखते हैं, ऐसा जानने को मिला है। इस सूचना की जाँच करने के लिए 1024 आगणकों को नियुक्त कियाजाता है। प्रत्येकसंशोधक आगणकों, यहविद्यार्थियों की समष्टि में से यादृच्छिक रीति से 10 विद्यार्थियों को पसंद करके उसकी चोकलेट खाने की आदत के बारे में जाँच करता है, तो 30% से कम विद्यार्थी चोकलेट खाने की आदत रखते है ऐसी जानकारी देनेदाले आगणकों की अपेक्षित संख्या ज्ञात कीजिए।
उत्तर :
चोकलेट खाने की आदत हो उसे सफलता गिनने पर
P = \(\frac {50}{100}\) = 0.5 ∴ q = 1 – p = 1 – 0.5 = 0.5 ∴ q = 0.5
10 विद्यार्थीयों को चयन किया जाता है इसलिए n = 10
30% से कम विद्यार्थी चोकलेट की आदत रखते है ∴ \(\frac{10 \times 30}{100}\) = 3 से कम विद्याथा x = 0, 1, 2
द्विपद वितरण का संभावना सूत्र P (x) = ⁿC_x P^xq^{n – x} x = 0, 1, 2….n
n = 10, x = 0, 1, 2 P = 0.5 q = 0.5 रखने पर P = \(\frac {1}{2}\), q = \(\frac {1}{2}\)