GSEB Solutions Class 12 Statistics Part 2 Chapter 3 प्रामाण्य-वितरण Ex 3

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 3 प्रामाण्य-वितरण Ex 3 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 3 प्रामाण्य-वितरण Ex 3

विभाग – A

निम्न दिये गए विकल्पों में से सही विकल्प चुन करके लिखिए।

प्रश्न 1.
निम्न में से μ(माध्य) और δ(प्रमाणित विचलन ) वाला प्रामाण्य चल x का संभावना घटत्व फलन कौन-सा है?

उत्तर :

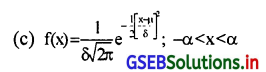
प्रश्न 2.
एक प्रामाण्य चल x का माध्य μ और प्रमाप विचलन 8 है; तो उसका प्रमाणित प्रामाण्य चल Z निम्न में से कौन-सा होगा?
(a) Z = \(\frac{x-\delta}{\mu}\)
(b) Z = \(\frac{\delta-x}{\mu}\)
(c) Z = \(\frac{\mu-x}{\delta}\)
(d) Z = \(\frac{x-\mu}{\delta}\)
उत्तर :
(d) Z = \(\frac{x-\mu}{\delta}\)

प्रश्न 3.
प्रमाणित प्रामाण्य चल का संभावना घटत्व फलन निम्न में से कौन-सा है ?

उत्तर :

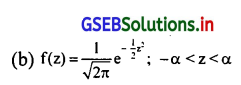
प्रश्न 4.
प्रमाणित प्रामाण्य चल का माध्य और विचरण निम्न में से कौन-सा है?
(a) माध्य = 0, विचरण = 1
(b) माध्य = 1, विचरण = 0
(c) विचरण = 0, माध्य = 0
(d) माध्य = 1, विचरण = 1
उत्तर :
(a) माध्य = 0, विचरण = 1

प्रश्न 5.
प्रामाण्य वक्र का कुल क्षेत्रफल निम्न में से कौन-सा है?
(a) -1
(b) 0
(c) 1
(d) 0.5
उत्तर :
(c) 1

प्रश्न 6.
प्रामाण्य वक्र में 4 से दाईं ओर का क्षेत्रफल कितना होता है?
(a) 0
(b) 0.5
(c) 1
(d) -0.5
उत्तर :
(b) 0.5

प्रश्न 7.
प्रामाण्य वितरण में 99% अवलोकनों सामान्य रीति से निम्न में से कौन-सी सीमा में होते है?
(a) μ ± 1.96δ
(b) μ ± 2δ
(c) μ ± 3δ
(d) μ ± 2.575δ
उत्तर :
(d) μ ± 2.575δ

प्रश्न 8.
प्रामाण्य वितरण के सामान्य रीति से कितने प्रतिशत अवलोकन μ ± δ की सीमा में होते है?
(a) 34.13%
(b) 95.45%
(c) 68.26%
(d) 50%
उत्तर :
(c) 68.26%

प्रश्न 9.
प्रामाण्य चल के लिए औसत विचलन का अनुमानित मूल्य निम्न में से कौन-सा है?
(a) \(\frac {4}{5}\)δ
(b) \(\frac {4}{5}\)μ
(c) \(\frac {2}{3}\)δ
(d) \(\frac {2}{3}\)μ
उत्तर :
(a) \(\frac {4}{5}\)δ

प्रश्न 10.
प्रमाणित प्रामाण्य चल के लिए चतुर्थक विचलन का अनुमानित मूल्य निम्न में से कौन-सा है?
(a) \(\frac {2}{3}\)δ
(b) \(\frac {2}{3}\)
(c) \(\frac {4}{5}\)δ
(d) \(\frac {4}{5}\)
उत्तर :
(b) \(\frac {2}{3}\)

प्रश्न 11.
प्रामाण्य वितरण के लिए माध्य और प्रथम चतुर्थक क्रमशः 11 और 3 है, तो तृतीय चतुर्थक का मूल्य निम्न में से कौन-सा होगा?
(a) 8
(b) 14
(c) 19
(d) 10
उत्तर :
(c) 19

प्रश्न 12.
एक प्रामाण्य वितरण के लिए औसत विचलन का अंदाजित मूल्य 20 है, तो उस वितरण का चतुर्थक विचलन का मूल्य निम्न में से कौन-सा होगा?
(a) \(\frac {25}{3}\)
(b) \(\frac {32}{3}\)
(c) 24
(d) \(\frac {50}{3}\)
उत्तर :
(d) \(\frac {50}{3}\)

प्रश्न 13.
प्रामाण्य वितरण के प्रचलित संकेत में यदि x = 25, μ = 20 और δ = 5 हो, तो प्रमाणित प्रामाण्य प्राप्तांक का मूल्य निम्न में से कौन-सा होगा?
(a) 1
(b) -1
(c) 4
(d) \(\frac {10}{3}\)
उत्तर :
(a) 1

प्रश्न 14.
एक प्रामाण्य चल का माध्य 50 है। यदि x = 25 के लिए Z प्राप्तांक का मूल्य -2.5 हो, तो वितरण का विचरण का मूल्य निम्न में से कौन-सा होगा?
(a) 10
(b) 100
(c) 50
(d) 25
उत्तर :
(b) 100

प्रश्न 15.
एक प्रामाण्य चल का वितरण N(20, 4) से दर्शाया गया है, तो उसके 99.33% अवलोकन निम्न में से कौन से अंतराल में होगा?
(a) (18, 22)
(b) (16, 24)
(c) (14, 26)
(d) (12, 28)
उत्तरः
(c) (14, 26)

विभाग – B

निम्न प्रश्नों के उत्तर एक वाक्य में लिखिए।

प्रश्न 1.
प्रामाण्य चल के घटत्व फलन में उपयोग में लिए जाते अचलांकों के मूल्य बताइए।
उत्तर :
प्रामाण्य चल के अचलांक π = 3.1416 और e = 2.7183 है।

प्रश्न 2.
सतत यादृच्छिक चल किसी एक निश्चित मूल्य धारण करे उसकी संभावना कितनी होगी?
उत्तर :
सतत यादृच्छिक चल x की एक निश्चित मूल्य के लिए संभावना घटत्व फलन द्वारा प्राप्त संभावना हमेशां शून्य (0) होता है।

प्रश्न 3.
प्रामाण्य वक्र का आकार कैसा होता है?
उत्तर :
प्रामाण्य वक्र का आकार संपूर्ण घंटाकार स्वरूप का होता है।

प्रश्न 4.
प्रामाण्य वितरण की विषमता कितनी होती है?
उत्तरः
प्रामाण्य वितरण की विषमता शून्य (0) होती है।

प्रश्न 5.
“प्रमाणित प्राप्तांक माप की इकाई से मुक्त होता है” यह विधान सत्य है या असत्य ?
उत्तर :
विधान सत्य है क्योंकि प्रमाणित प्राप्तांक माप की इकाई से मुक्त होते है उसे इकाई में दर्शाया नहीं जाता है।

प्रश्न 6.
प्रमाणित प्रामाण्य वक्र यह प्रमाणित प्रामाण्य चल के कौन-से मूल्य के दोनों ओर संमित होता है?
उत्तर :
प्रमाणित प्रामाण्य वक्र में x के माध्य µ की दोनों ओर संमित होता z = 0 शिर्ष लंब रेखा से दोनों ओर संमित होता है।

प्रश्न 7.
प्रामाण्य वक्र में प्रामाण्य चल की कौन-सी किंमत के लिए शिर्ष लंब रेखा प्रामाण्य वक्र के क्षेत्रफल को दो समान भागों में बाँटती है?
उत्तर :
प्रमाणित वक्र में प्रामाण्य चल की माध्य µ की दोनों ओर क्षेत्रफल समान होता है अर्थात् दो समान भाग x = µ शिर्ष लंबरेखा से दो समान भाग
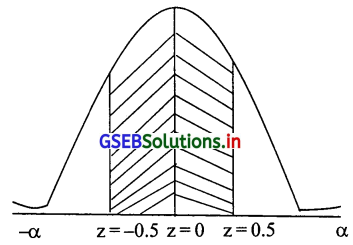
होता है। दोनों तरफ का क्षेत्रफल 0.5 समान होता है।

प्रश्न 8.
प्रामाण्य वक्र में µ – 2δ और µ + 2δ के बीच आनेवाले क्षेत्रफल कितने प्रतिशत होता है?
उत्तर :
µ – 2δ और µ + 2δ के बीच का क्षेत्रफल 0.9545 है इसलिए दोनों के बीच 0.9545 × 100 = 95.45% क्षेत्रफल आयेगा।

प्रश्न 9.
एक प्रामाण्य वितरण का माध्य 13.25 और प्रमाप विचलन 10 हो, तो उसके तृतीय चतुर्थक की अंदाजित किंमत बताइए।
उत्तर :
µ = 13.25 और δ = 10 है। Q₃ ज्ञात करने के लिए निम्न अनुमानितता युक्त सूत्र का उपयोग करेंगे।
Q₃ = µ + 0.675δ = 13.25 + 0.675 × 10 = 13.25 + 6.75
Q₃ = 20 ∴ Q₃ = 20 तृतीय चतुर्थक = 20

प्रश्न 10.
10 माध्य और 6 प्रमाणित विचलनवाला प्रामाण्य वितरण के लिए चतुर्थक विचलन का अनुमानित मूल्य ज्ञात कीजिए।
उत्तर :
चतुर्थक विचलन की अनुमानित मूल्य = \(\frac {2}{3}\)δ = \(\frac {2}{3}\) × 6 = \(\frac {12}{3}\) ∴ चतुर्थक विचलन की अनुमानित मूल्य = 4

प्रश्न 11.
एक प्रामाण्य वितरण के लिए औसत विचलन का अनुमानित मूल्य 8 हो, तो उस वितरण का प्रमाप विचलन ज्ञात कीजिए।
उत्तर :
औसत विचलन का अनुमानित मूल्य 8 है।
∴ औसत विचलन का अनुमानित मूल्य = \(\frac {4}{5}\)δ , 8 = \(\frac {4}{5}\) ∴ δ = \(\frac{8 \times 5}{4}\) δ = 10 प्रमाप विचलन = 10

प्रश्न 12.
एक प्रामाण्य वितरण के लिए चतुर्थक विचलन की अंदाजित किंमत 12 है, तो प्रमाप विचलन का मूल्य ज्ञात कीजिए।
उत्तर :
चतुर्थक विचलन का अंदाजित किंमत 12 है।
∴ चतुर्थक विचलन = \(\frac {2}{3}\)δ (लगभग) 12 = \(\frac {2}{3}\)δ ∴ δ = \(\frac{12 \times 3}{2}\) ∴ δ = 18 प्रमाप विमलन = 18

प्रश्न 13.
प्रमाणित प्रामाण्य चल के संभावना-वितरण के मध्य के 50% अवलोकन का मूल्य की अनुमानित मूल्य की सीमाएँ लिखिए।
उत्तर :
मध्य के 50% अवलोकन का मूल्य अर्थात् शिर्ष लंब रेखा से बायी ओर 25% और दायी ओर 25% आयेगा।

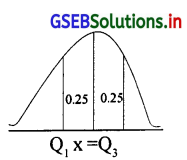
Q₁ और Q₃ के मूल्य के बीच 50% अवलोकन होगा।
∴ Q₁ = -0.675 और Q₃ = 0.675 (-0.675, 0.675) के अंतराल मे मध्य के 50% अवलोकन होंगे।

प्रश्न 14.
एक प्रामाण्य वितरण के अंतिम चतुर्थकों 20 और 30 हो, तो उसका माध्य ज्ञात कीजिए।
उत्तर :
अंतिम चतुर्थकों 20 और 30 दिया है। ∴ Q₁ = 20 और Q₃ = 30 होगा। प्रामाण्य वितरण में ∴ \(\overline{\mathrm{x}}\) = m = m₀
∴ m = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1}{2}=\frac{30+20}{2}=\frac{50}{2}\), M = 25
∴ M = 25 समान होते है ∴ \(\overline{\mathrm{x}}\) = माध्य 25 होगा माध्य = 25

प्रश्न 15.
व्यक्तियों के एक समूह में व्यक्तियों का मासिक खर्च प्रामाण्य वितरण को अनुसरता है। यदि औसत खर्च ₹ 10,000 और प्रमाप विचलन ₹ 1,000 हो, तो याद्दच्छिक रीति से चयन किया गया व्यक्ति का मासिक खर्च ₹ 11,000 से अधिक होने के लिए किसी एक विद्यार्थी का z प्राप्तांक = ₹ 1 मिलता है, तो क्या z – प्राप्तांक की यहगणना सत्य है ? क्यों कारणं दीजिए।
उत्तर :
z की गणना 1 मिलता है वह असत्य है क्योंकि
z = \(\frac{x-\mu}{\delta}=\frac{11000-10000}{1000}=\frac{1000}{1000}\)
z = 1 से अधिक होगा।

प्रश्न 16.
एकसमूहके व्यक्तियों के उम्र का माध्य45 वर्षऔर प्रमापविचलन 10 वर्ष हो,वहप्रामाण्य वितरणको अनुसरताहै।यादृच्छिकरीति से पसंद हुए व्यक्तियों की उम्र 60 वर्ष हो उसके लिए z – प्राप्तांक की गणना कीजिए।
उत्तर :
µ = 45 और δ = 10 x = 60 वर्ष हो उसके लिए
z = \(\frac{x_1-\mu}{\delta}=\frac{60-45}{10}=\frac{15}{10}\)
z = 1.5

प्रश्न 17.
एक विद्यालय के विद्यार्थियों के अर्थशास्त्र विषय में प्राप्तनंबर का वितरण µ और δ वाला प्रमापविचलनवाला प्रामाण्य वितरण है।यादृच्छिक रीति से चयन किया गया विद्यार्थियों के गुण 60 हो, तो उसका प्रमाणित प्राप्तांक का मूल्य 1 है। यदि चल का विचरण 100 (नंबर)² हो, तो औसत नंबर ज्ञात कीजिए।
उत्तर :
विद्यार्थी का नंबर 60 है । ∴ x₁ = 60 प्रमाणित प्राप्तांक का मूल्य 1 है। ∴ z = 1
विचरण = δ² = 100 ∴ δ = 10 औसत नंबर (माध्य) = µ ज्ञात करना है
∴ z = \(\frac{x_1-\mu}{\delta}\) में मूल्य रखने पर 1 = \(\frac{60-\mu}{10}\) = 10 = 60 – µ
∴ µ = 60 – 10 µ = 50 माध्य (औसत नंबर) = 50

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
सतत चल के संभावना घटत्व फलन की परिभाषा दीजिए।
उत्तर :
याद्दच्छिक चल x समुच्चय R में अथवा उसका उपसमुच्चय हो ऐसे अन्तराल जो किसी भी मूल्य को धारण करने में समर्थ हो, तो उस चल x को सतत यादृच्छिक चल कहते है।

प्रश्न 2.
सतत चल के संभावना घटत्व फलन की शर्ते बताइए।
उत्तर :
सतत चल के संभावना घटत्व फलन की शर्ते

1. सतत चल दो सीमा के किसी भी मूल्य को धारण कर सकता है।
2. अन्तराल (0, α ) के घटकों सी संख्या अगण्य, अनन्त कहलाएगी।
3. संभावना घटत्व फलन द्वारा प्राप्त संभावना हमेशां शून्य (0) होता है।

प्रश्न 3.
प्रामाण्य वक्र कौन-सी विधि से प्राप्त किया जाता है?
उत्तर :
प्रामाण्य वक्र यह प्रामाण्य चल x के माध्य µ की दोनों ओर संमित होता है इसलिए x = µ शिर्षलंबरेखा के प्रामाण्य वक्र क्षेत्रफल को दो हिस्सा में विभाजीत करता है। x = µ की बायी और दांयी ओर क्षेत्रफल 0.5 होता है। उसे संकेत में P(x ≥ µ) = 0.5 या P(x ≤ µ) = 0.5 से दर्शाया जाता है।

प्रामाण्य वक्र के प्रदेश का क्षेत्रफल जानने हेतु सर्वप्रथम प्रामाण्य चलx के प्रमाणित प्रामाण्य चल z में परिवर्तन किया जाता है। प्रमाणित प्रामाण्य चल z की भिन्न भिन्न धन मूल्यों के लिए प्रामाण्य वक्र के 0 से Z तक का क्षेत्रफल सारणी पर से प्राप्त किया जाता है।

प्रश्न 4.
प्रामाण्य चल का संभावना फलन को परिभाषित कीजिए।
उत्तर :
सतत चल के संभावना-वितरण में प्रामाण्य वितरण अति महत्त्व का है। उसकी परिभाषा निम्नानुसार दे सकते है।
यदि याद्दच्छिक चल x यह µ (म्यु) माध्य और 6 (सिग्मा) वाला प्रमाणित विचलन हो और उसका संभावना घटत्व फलन
f(x) = \(\frac{1}{\delta \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\delta}\right)^2}\) ;-α < x < α
जहाँ π = 3.1416 और e = 27183 अचलांक हो, तो प्रामाण्य चल x का वितरण को प्रामाण्य चल और f(x) को प्रामाण्य चल का संभावना
घटत्व फलन से दर्शाया जाता है।

प्रश्न 5.
प्रमाणित प्रामाण्य वक्र का आकार कैसा होता है और उस चल की कौन-सी किंमत के सापेक्ष में संमित होता है?
उत्तर :
प्रमाणित प्रामाण्य वक्र का आकार संपूर्ण घण्टाकार वक्र है और x अक्ष और वक्र के बीच आच्छादित प्रदेश का कुल क्षेत्रफल 1 होता है। प्रामाण्य वक्र यह प्रामाण्य चल x के माध्य µ की दोनों ओर संमित होता है। P(x ≥ µ)= 0.5 और P(x ≤ µ) = 0.5 बायी-दायी ओर का क्षेत्रफल प्राप्त
होता है।

प्रश्न 6.
प्रमाणित प्रामाण्य चल की परिभाषा देकर उसका संभावना घटत्व फलन लिखिए।
उत्तर :
यदि प्रामाण्य याद्दच्छिक चल x का माध्य µ और प्रमाप विचलन δ हो, तो यादृच्छिक चल z = \(\frac{x-\mu}{\delta}\) को प्रमाणित प्रामाण्य चल कहते है।
प्रमाणित प्रामाण्य चल का घटत्व फलन निम्नानुसार है
f(z) = \(\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{1}{2} 2^2}\);-α < z < α जहाँ z = \(\frac{x-\mu}{\delta}\)

प्रश्न 7.
प्रामाण्य चल x का संभावना घटत्व फलन f(x) = अचलांक \(x e^{-\frac{1}{50}(x-10)^2}\);-α < x < α है, तो इस सूचना से प्रथम चतुर्थक ज्ञात कीजिए।
उत्तर :
प्रामाण्य चल f(x)= \(\frac{1}{\delta \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\delta}\right)^2}\);-α< x < α के साथ तुलना करने पर µ = 10 और δ = 5 प्राप्त होगा।
अब प्रथम चतुर्थक (Q₁)सूत्र पर से
Q₁ = µ = 0.675δ = 10 – 0.675(5) = 10 – 3.375 = 6.625 ∴ Q₁ = 6.63

प्रश्न 8.
एक प्रामाण्य चल के अंतिम चतुर्थक 10 और 30 हो, तो उसका औसत विचलन ज्ञात कीजिए।
उत्तर :
प्रामाण्य चल के अंतिम चतुर्थक 10 और 30 है। इसलिए Q₁ = 10 और Q₃ = 30 प्रथम चतुर्थक विचलन ज्ञात करेंगे।
चतुर्थक विचलन = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}=\frac{30-10}{2}=\frac{20}{2}\) चतुर्थक विचलन = 10
चतुर्थक विचलन = \(\frac {2}{3}\)δ 10 = \(\frac {2}{3}\)δ ∴ δ\(\frac{10 \times 3}{2}\) ∴ δ = 15
अब औसत विचलन = \(\frac {4}{5}\)δ = \(\frac {4}{5}\) × 15 = 12 औसत विचलन = 12

प्रश्न 9.
एक प्रामाण्य चल के लिए औसत विचलन 48 हैऔरतृतीय चतुर्थक 120 है,तो प्रथमचतुर्थककीअनुमानितकिंमत प्राप्त कीजिए।
उत्तर :
औसत विचलन 48 और तृतीय चतुर्थक 120 दिया है।
∴ औसत विचलन = \(\frac {4}{5}\)δ 48 = \(\frac {4}{5}\)δ = ∴ δ = \(\frac{48 \times 5}{4}\) δ = 60
अब चतुर्थक विचलन = \(\frac {2}{3}\)δ = \(\frac {2}{3}\) × 60 चतुर्थक विचलन = 40
चतुर्थक विचलन = \(\frac{Q_3-Q_1}{2}\) 40 = \(\frac{120-Q_1}{2}\) 80 = 120 – Q₁ Q₁ = 120 – 80 ∴ Q₁= 40
प्रथम चतुर्थक = 40

प्रश्न 10.
एक प्रामाण्य चल x के लिए संभावना घटत्व फलन निम्नानुसार है।
f(x) = \(\frac{1}{10 \sqrt{2+1}} e^{-\frac{1}{2}\left(\frac{x-100}{10}\right)^2}\)7;-α< x < α यह वितरण का मध्य के 68.26% अवलोकनों की सीमा का अनुमान कीजिए।
उत्तर :
प्रामाण्य चल का घटत्व फलन f(x) = \(\frac{1}{\delta \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{8}\right)^2}\) – α < x < α के साथ तुलना करने पर δ = 10और µ = 100
प्रामाण्य वितरण के मध्य में 68.28% मे अवलोकन µ ± δ के अंतराल में है।
(µ – 1δ)(µ + 1δ) ∴ (100 – 1 × 10; 100 + 1 × 10)
∴ (100 – 10; 100 + 10) ∴ (90, 110)
दी गई सूचना पर से प्रामाण्य वितरण के 68.26% अवलोकन 90 से 110 के बीच होंगे।

प्रश्न 11.
प्रमाणित प्रामाण्य चल का मूल्य 0 और z प्राप्तांक (z₁) के बीच होने की संभावना 0.4950 हो, तो z प्राप्तांक की संभवतः मूल्य ज्ञात कीजिए।
उत्तर :
माना कि z₁ > 0 है, z₁ यह z = 0 की दायी ओर होगा और P(0 ≤ z ≤ z₁) = 0.4950 है।

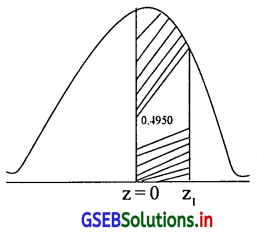
अब 0.4950 के लिए तालिका के विलोम रूप में देखने पर z₁ का मूल्य 2.57 और 2.58 की औसत लेने पर \(\frac{2.57+2.58}{2}\) z₁ = 2.575 मिलता है। इसलिए z₁ = 2.575 उसी प्रकार बायी ओर के लिए z₁ का मूल्य z₁ = -2.575 प्राप्त होगा। ∴ z₁ = -2.575 अर्थात् z₁ = ± 2.575

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए।

प्रश्न 1.
प्रामाण्य वितरण की परिभाषा दीजिए एवं प्रामाण्य वक्र के लक्षण बताइए।
उत्तर :
जिस यादृच्छिक चर x का संभावना घटत्व फलन का आलेख चित्र संपूर्ण घण्टाकार स्वरूप का हो, उस संभावना-वितरण को प्रामाण्य वितरण कहते है।

प्रामाण्य वक्र के लक्षणः

1. प्रामाण्य वक्र का आलेख संपूर्ण घण्टाकार स्वरूप का होता है।
2. प्रामाण्य वक्र z = 0 की दोनों ओर संमित होता है।
3. प्रामाण्य वक्र यह प्रामाण्य चल का संभावना घटत्व फलन का वक्र है।
4. x अक्ष के बीच का आच्छादित प्रदेश का कुल क्षेत्रफल (संभावना) 1 होता है।
5. x = µ शिर्षलंब रेखा प्रामाण्य वक्र का दो समान हिस्सा करती है। x = µ की बायी और दायीं ओर का क्षेत्रफल 0.5 होता है।

प्रश्न 2.
प्रामाण्य वितरण का गुणधर्म बताइए।
उत्तर :
प्रामाण्य वितरण का गुणधर्म (विशेषताएँ) निम्नलिखित है :

1. यह सतत याद्दच्छिक चल का संभावना-वितरण है।
2. µ और δ इसके प्राचल है।
3. यह वितरण µ के सापक्ष संमित है और उसकी विषमता शून्य (0) है।
4. इस वितरण का संभावना फलन का आरेख चित्र घण्टाकार होता है और सतत वक्र है।
5. इस वितरण में माध्य, मध्यका और भूयिष्ठक का मूल्य समान होता है। संकेत में µ = m = m₀ होता है।
6. इस वितरण में चतुर्थक मध्यका से समान अंतर पर है अर्थात् Q₃ – M = M – Q₁ और M = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1}{2}\)
7. इस बंटन के प्रायिकता – घटत्व फलन के वक्र के दोनों किनारे x अक्ष को अनंतलक्षी है।
8. इस बंटन के अंतिम चतुर्थकों का अनुमानित मूल्य निम्न सूत्र से प्राप्त किए जाते है। Q₁ ≅ µ – 0.675δ Q₃ ≅ µ + 0.675δ
9. इस वितरण का चतुर्थक विचलन = \(\frac {2}{3}\)δ (लगभग) है।
10. इस वितरण का औसत विचलन =\(\frac {4}{5}\)2δ (लगभग) है।
11. प्रामाण्य वक्र के महत्त्वपूर्ण क्षेत्रफल निम्नानुसार है :
    • प्रामाण्य वक्र का कुल क्षेत्रफल 1 होता है और x = µ शिर्षलंब रेखा की दोनों ओर क्षेत्रफल 0.5 होता है।
    • वक्र की शिर्षलंब रेखा µ – δ और µ + δ के बीच आनेवाले प्रदेश का क्षेत्रफल 0.6826 है।
    • वक्र की शिर्षलंब रेखा µ – 2δ और µ + 2δ के बीच आनेवाले प्रदेश का क्षेत्रफल 0.9545 है।
    • वक्र की शिर्षलंब रेखा µ – 3δ और µ + 3δ के बीच आनेवाले प्रदेश का क्षेत्रफल 0.9973 है।
    • वक्र की शिर्षलंब रेखा µ – 1.966 और µ + 1.966 के बीच आनेवाले प्रदेश का क्षेत्रफल 0.95 है।
    • वक्र की शिर्षलंब रेखा µ ± 2.5756 के बीच आनेवाले प्रदेश का क्षेत्रफल 0.99 है।

प्रश्न 3.
प्रमाणित प्रामाण्य वितरण के गुणधर्म बताइए।
उत्तर :
प्रमाणित प्रामाण्य वितरण के गुणधर्म निम्नलिखित है :

1. इस वितरण सतत याद्दच्छिक चल का वितरण है।
2. इस वितरण का माध्य 0 (शून्य) और विचरण एवं प्रमाप विचलन 1 (एक) है।
3. इस बंटन में माध्य, मध्यका और भूयिष्ठक के मूल्य समान होते है अर्थात् शून्य होगा।
4. इस वितरण z = 0 के सापेक्ष संमित है और उसकी विषमता शून्य है।
5. इसमें प्रथम चतुर्थक का अनुमानित मूल्य Q₁ = -0.675 एवं तृतीय चतुर्थक का अनुमानित मूल्य Q₃ = 0.675 होता है।
6. इस वितरण में चतुर्थक विचलन का अनुमानित मूल्य = 2/3 है।
7. इस वितरण में औसत विचलन का अनुमानित मूल्य = 4/5 है।
8. प्रमाणित प्रामाण्य वक्र के महत्त्वपूर्ण क्षेत्रफल निम्नानुसार है :
   • प्रमाणित प्रामाण्य वक्र में कुल क्षेत्रफल 1 है और z = 0 शिर्षलंब रेखा से दोनों ओर क्षेत्रफल 0.5 होता है।
   • वक्र की शिर्षलंब रेखाएँ z = -1 और z + 1 के बीच का क्षेत्रफल 0.6826 है।
   • वक्र की शिर्षलंब रेखाएँ z = -2 और z = +2 के बीच का क्षेत्रफल 0.9545 है।
   • वक्र की शिर्षलंब रेखाएँ z = -3 और z = +3 के बीच का क्षेत्रफल 0.9973 है।
   • वक्र की शिर्षलंब रेखाएँ z = -1.96 और z = + 1.96 के बीच का क्षेत्रफल 0.95 है।
   • वक्र की शिर्षलंब रेखाएँ z = -2.575 और z = + 2.575 के बीच का क्षेत्रफल 0.99 है।

प्रश्न 4.
एक प्रामाण्य वितरण का माध्य 50 और विचरण 9 है, तो
(i) प्रामाण्य चल x का मूल्य 50 और 53 के बीच होने की
(ii) प्रामाण्य चल x का मूल्य 47 और 53 के बीच होने की संभावना ज्ञात कीजिए।
उत्तर
माध्य = μ = 50 और विचरण = δ² = 9 है ∴ प्रमाप विचलन δ = 3
(i) प्रामाण्य चल x का मूल्य 50 और 53 के बीच होने की संभावना
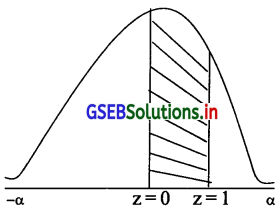
= P(50 ≤ × ≤ 53) = P(\(\frac{50-50}{3} \leq \frac{x-\mu}{\delta} \leq \frac{53-50}{3}\)) = (0 ≤ z ≤ 1)
P = (0 ≤ z ≤ 1) = 0.3413
याद्दच्छिक चल 50 और 53 के बीच होने की संभावना = 0.3413

(ii) प्रामाण्य चल x का मूल्य 47 और 53 के बीच होने की संभावना
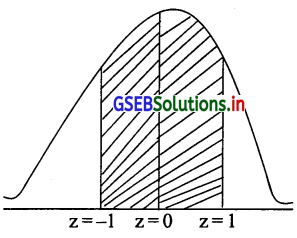
= P(47 ≤ × ≤ 53) = P(\(\frac{47-50}{3} \leq \frac{x-\mu}{\delta} \leq \frac{53-50}{3}\)) = P(-1 ≤ z ≤ 1)
= P(-1 ≤ z ≤ 0) + P(0 ≤ z ≤ 1)
= P(0 ≤ z ≤ 1) + P(0 ≤ z ≤ 1)
= 0.3413 + 0.3413 = 0.6826
प्रामाण्य चल x का मूल्य 47 और 53 के बीच होने की संभावना 0.6826

प्रश्न 5.
यदि चल x यह 100 माध्य और 15 प्रमाप विचलनवाला प्रामाण्य चल हो,तो
(i) वितरण में कितने प्रतिशत अवलोकन का मूल्य 85 से अधिक होगा?
(ii) वितरण में कितने प्रतिशत अवलोकन का मूल्य 130 से कम होगा?
उत्तरः
माध्य = µ = 100, प्रमाप विचलन = δ = 15
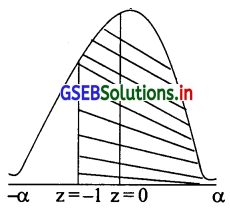
(i) वितरण में कितने प्रतिशत अवलोकन का मूल्य 85 से अधिक होगा?
= P(x ≥ 85) = P(\(\frac{x-\mu}{8} \geq \frac{85-100}{15}\)) = P(z ≥ -1)
= P(-1 ≤ z ≤ 0) + P(0 ≤ z ≤ α)
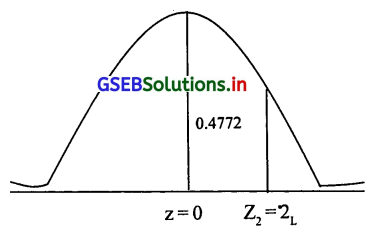
= 0.3413 + 0.5 (प्रमाणित प्रामाण्य चल की सारणी पर से) = 0.8413
85 से अधिक अवलोकन की प्रतिशतता = 100 × 0.8413 = 84.13%
84.13% अवलोकन 85 से अधिक होंगे।

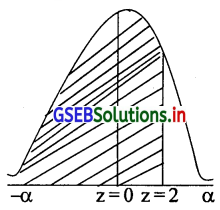
(ii) वितरण में कितने प्रतिशत अवलोकन का मूल्य 130 से कम होगा।
P(x ≤ 130) = P(\(\frac{x-\mu}{\delta} \leq \frac{130-100}{15}\)) = P(z ≤ 2)
= P(-α < z ≤ 0) + P(0 ≤ z ≤ 2)
= 0.5 + 0.4772 = 0.9772
130 से कम अवलोकन की प्रतिशतता = 100 × 0.9772 = 97.72%
97.72% अवलोकन 130 से कम होंगे।

प्रश्न 6.
शहर के एक विस्तार में से चयन किये 500 वयस्क व्यक्तियों का वजन प्रामाण्य वितरण को अनुलक्षित है। यहव्यक्तियों का औसत वजन 55 कि.ग्रा.और प्रमाप विचलन 7 कि.ग्रा. हो, तो
(1) उस विस्तार में 41 कि.ग्रा.और 62 कि.ग्रा. के बीच वजनवाले व्यक्तियों की संख्या का अनुमान कीजिए।
(2) उस विस्तार में 41 कि.ग्रा. से कम वजनवाली व्यक्तियों की संख्या का अनुमान करो।
उत्तरः
N = 500, µ = 55, S = 7

(1) उस विस्तार में 41 कि.ग्रा. और 62 कि.ग्रा. के बीच वजनवाले व्यक्तियों की संख्या का अनुमान
P(41 ≤ x ≤ 62) = P(\(\frac{41-55}{7} \leq \frac{x-\mu}{\delta} \leq \frac{62-55}{7}\)) = P(\(\frac{-14}{7} \leq \frac{x-\mu}{\delta} \leq \frac{7}{7}\)) P(-2 ≤ z ≤ 1)
= P(-2 ≤ z ≤ 0) + P(0 ≤ z ≤ 1)
= 0.4772 + 0.3413 = 0.8185
उस विस्तार के 41 कि.ग्रा. से 62 कि.ग्रा. के बीच वजनवाले व्यक्तियों की संख्या
= N × 0.8185 = 500 × 0.8185 = 409.25 = 409 व्यक्ति
41 कि.ग्रा. से 62 कि.ग्रा. के बीच व्यक्तियों की संख्या =409 (लगभग)

(2) उस विस्तार में 41 कि.ग्रा. से कम वजनवाली व्यक्तियों की संख्या
P(x ≤ 41) = P(\(\frac{x-\mu}{\delta} \leq \frac{41-55}{7}\)) = P(z ≤ \(\frac{-14}{7}\)) = P( z ≤ – 2)
=P(-α < z ≤ 0) – P(-2 ≤ z ≤ 0)
= 0.5 – P(0 ≤ z ≤ 2) = 0.5 – 0.4772 = 0.0228
41 कि.ग्रा. से कम वजनवाले व्यक्तियों की संख्या = N × 0.0228
= 500 × 0.0228 = 11.4
≅ 11 व्यक्ति
41 कि.ग्रा. से कम वजनवाले व्यक्तियों की संख्या = 11 लगभग

प्रश्न 7.
यदि यह प्रमाणित प्रामाण्य चल हो,तो निम्नशों का समाधान हो इस रीति से z- प्राप्तांक (z₁) का मूल्यों का अनुमानज्ञात कीजिए।
(1) Z = z₁ के बाई ओर का क्षेत्रफल 0.9928 है।
(2) Z = z₁ के दाई ओर का क्षेत्रफल 0.0250 है।
उत्तर
(1) यहाँ z = z₁ के बाई ओर का क्षेत्रफल 0.9928 है अर्थात् P(Z <z₁) = 0.9928 है। प्रामाण्य वक्र में Z = z₁ की शिर्षलंबरेखा खिंचने के लिए वक्र का बाई ओर से दाई ओर के लिए 0.9928 क्षेत्रफल मिले ऐसी आकृति निम्नानुसार खिचेंगे।

P(Z < z₁) = P(-α < z < 0) + P(0 ≤ 2 ≤ z₁) = 0.9928
∴ 0.5 + P(0 ≤ z ≤ z₁) = 0.9928
∴ P(0 ≤ z ≤ z₁) = 0.9928 – 0.5
∴ P(0 ≤ z ≤ z₁) = 0.4928
संभावना 0.4928 के अनुरूप z₁ का मूल्य प्रमाणित प्रामाण्य चल की सारणी पर से विलोम रूप से देखने पर

सारणी पर से	क्षेत्रफल	Z प्राप्तांक
0.4928 के पहले की नजदीक का मूल्य	0.4927	2.44
0.4928 के बाद की नजदीक का मूल्य	0.4929	2.45
औसत मूल्य	0.4928	2.445

उपर्युक्त सारणी से स्पष्ट होता है कि z₁ = 2.445

(2) Z = z₁ की दाई ओर का क्षेत्रफल = 0.0250 है अर्थात् P(Z ≥ z₁)= 0.0250 प्रामाण्य वक्र में Z = z₁ की शिर्षलंब रेखा ऐसे खिचेंगे जो दायीं ओर वक्र के दाई ओर कोने में क्षेत्रफल 0.0250 होगा। उसका वक्र निम्नानुसार खिचेंगे।

P(Z ≥ z₁) = P(0 < x ≤ a)- P(0 ≤ z ≤ z₁)= 0.0250
= 0.5000 – P(0 ≤ z ≤ z₁) = 0.0250
= P(0 ≤ z ≤ z₁) = 0.5 – 0.0250 = 0.4750
संभावना 0.4750 के अनुरूप z₁ का मूल्य z₁ का प्रामाण्य चल की सारणी विलोम रूप से देखने
पर ₁ = 1.96 ∴ z₁ = 1.96

प्रश्न 8.
यदि यह प्रमाणित प्रामाण्य चल हो, तो निम्नशर्तों का समाधान हो इस रीति से z – प्राप्तांक (z₁) का मूल्यों का अनुमानित मूल्य प्राप्त
कीजिए।
(1) Z = z₁ के बाई ओर का क्षेत्रफल 0.15 है।
(2) Z = z₁ की दाई ओर का क्षेत्रफल 0.75 है।
उत्तर :
(1) Z = z₁ की बाई ओर का क्षेत्रफल 0.15 है। अर्थात् P(Z ≤ z₁) = 0.15 है। प्रामाण्य वक्र में Z = z₁ की शिर्षलंब रेखा खिचने के लिए। बाँयी ओर 0.15 क्षेत्रफल मिले ऐसी आकृति निम्नानुसार खिचेंगे।

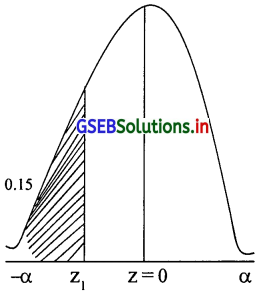
P(Z ≤ z₁) = P(-α ≤ z ≤ 0) – P(z₁ ≤ z ≤ 0) = 0.15
∴ 0.5 – P(z₁ ≤ z ≤ 0) = 0.15
∴ P(z₁ ≤ z ≤ 0) = 0.5 – 0.15
∴ P(z₁ ≤ z ≤ 0) = 0.35 क्षेत्रफल के लिए तालिका को विलोम रूप से देखने पर

सारणी पर से	क्षेत्रफल	Z प्राप्तांक
0.3500 के पहले की नजदीक का मूल्य	0.3485	1.03
0.3500 के बाद की नजदीक का मूल्य	0.3508	1.04
औसत मूल्य	0.3497	1.035

उपर्युक्त सारणी से स्पष्ट होता है कि z₁ = 1.035 बाई ओर के लिए z₁ = -1.035 होगा।

(2) Z = z₁ की दाई ओर का क्षेत्रफल 0.75 है। अर्थात् P(Z ≥ z₁)= 0.75 है। प्रामाण्य वक्र की Z = z₁ की शिर्षलंब रेखा खिंचने के लिए दाई ओर का क्षेत्रफल 0.75 होगा। उसका वक्र निम्नानुसार खिचेंगे।

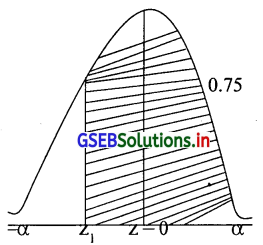
P(Z ≥ z₁) = P(z₁ ≤ z ≤ 0) + P(0 ≤ z ≤ α ) = 0.75
=P(z₁ ≤ z ≤ 0) + 0.5 = 0.75
∴ P(z₁ ≤ z ≤ 0) = 0.75 – 0.5
∴ P(z₁ ≤ z ≤ 0)= 0.25
संभावना 0.25 क्षेत्रफल के अनुरूप z₁ का मूल्य तालिका को विलोम रूप से देखने पर 0.2500 के पहले का नजदीक मूल्य 0.2486 है। उसकी संभावना 0.67 और 2500 के बाद कां नजदीक मूल्य 0.2518 के संभावना 0.68 है। दोनों की ओसत \(\frac{0.67+0.68}{2}\) = 0.675 z₁ का मूल्य z₁ = -0.675 होगा

प्रश्न 9.
यदि यह प्रमाणित प्रामाण्य चल हो और z₁ यहz- प्राप्तांक दर्शाता हो, तो निम्न शतों का समाधान हो ऐसे z₁ का मूल्य का अनुमान ज्ञात कीजिए।
(i) P(-2 ≤ Z ≤ z₁) = 0.2857
(ii) P(z₁ ≤ z ≤ 1.75) = 0.10
उत्तर :
(i) P(-2 ≤ z ≤ < z₁) = 0.2857 का वक्र निम्नानुसार खिचेंगे:

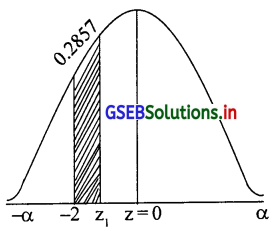
P(-2 ≤ z ≤ 0) – P(z₁ ≤ z ≤ 0) = 0.2857
0.4772 – P(z₁ ≤ z ≤ 0) = 0.2857
P(z₁ ≤ Z ≤ 0) = 0.4772 – 0.2857 = 0.1915
P(z₁ ≤ Z ≤ 0)= 0.1915 क्षेत्रफल के लिए तालिका को विलोम रूप से देखने पर
z₁ = 0.5 होगा।
z₁ = -0.5

(ii) P(z₁ ≤ z ≤ 1.75) = 0.10 का वक्र निम्नानुसार खिचेंगे:

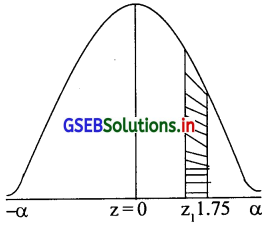
=P (0 ≤ z ≤ 1.75) – P(z₁ ≤ z ≤ 1.75) = 0.10
= 0.4599 – P(0 ≤ z ≤ z₁) = 0.10
= P(0 ≤ z ≤ z₁) = 0.4599 – 0.10
= 0.3599 क्षेत्रफल के लिए तालिका को विलोम रूप से देखने पर z₁ = 1.08 होगा।

प्रश्न 10.
एक कारखाना में मासिक उत्पादन यह औसत µ इकाई और प्रमाप विचलन 8 इकाई हो ऐसा प्रामाण्य वितरण को अनुसरता है। उत्पादन 2400 इकाई और 1800 इकाई हो, तो उसके लिएz-प्राप्तांक क्रमशः1 और-0.5 है, तो इस वितरणका माध्य और प्रमाप विचलन ज्ञात कीजिए।
उत्तर :

परिमाण (i) में δ = 400 रखने पर
6 = 2400 – µ ……….(1)
400 = 2400 – µ
µ = 2400 – 400
µ = 2000
माध्य = 2000 और प्रमाप विचलन = 400 होगा।

प्रश्न 11.
एक प्रामाण्य x चल संभावना घटत्व फलन निम्नानुसार है:
f(x) = \(\frac{1}{6 \sqrt{2 \pi}} e^{-\frac{1}{72}(x-100)^2}\);-α < x < α इस वितरण के बराबर मध्य के 50% अवलोकनों की अनुमानित सीमाएँ ज्ञात कीजिए।
उत्तर :
यहाँ µ = 100 δ = 6 बीचोबीच 50% अवलोकन का अन्तराल x₁ और x₂ है।

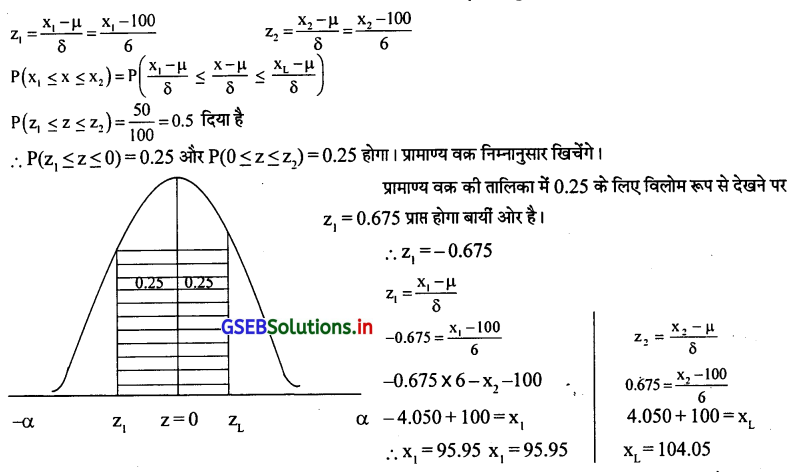
∴ Q₁ = 95.95 और Q₃ = 104.05 होगा अथवा Q₁ = µ – 0.6758 और Q₃ = µ + 0.6758 का उपयोग कर सकते है।

प्रश्न 12.
एक प्रामाण्य वितरण के लिए प्रथम चतुर्थक 35 और तृतीय चतुर्थक 65 है, तो वितरण के बीचोबीच मध्य के 95.45% प्राप्तांकों का अन्तराल ज्ञात कीजिए।
उत्तर :
यहाँ Q₁ = 35 और Q₃ = 65 है।

वितरण के मध्य की 95.45% अवलोकनों की सीमाएँ \(\frac{95.45}{100}=\frac{0.9545}{2}\) = 0.47725
µ + 2.000δ के है (µ – 2.000δ, µ + 2.000δ)
(50-2.005(22.5), 50 + 0.2000(22.5)) (50 – 45), (50 + 45) (5, 95)
बीच के 95.45% अवलोकन का अंतराल 5 से 95 होगा।

प्रश्न 13.
एक प्रामाण्य वितरण के लिए तृतीय चतुर्थक और औसत विचलन क्रमशः 36 और 24 है तो वितरण का माध्य ज्ञात कीजिए।
उत्तर :
तृतीय चतुर्थक = 36 और औसत विचलन = 24 है।
अथवा औसत विचलन = \(\frac {4}{5}\)δ 24 = \(\frac {4}{5}\)δ = \(\frac{24 \times 5}{4}\) = δ ∴ δ = 30
चतुर्थक विचलन = \(\frac {2}{3}\)δ = \(\frac {2}{3}\) x 30 चतुर्थक विचलन = 20
= \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}\) = 20 \(\frac{36-\mathrm{Q}_1}{2}\) = 20 36 – Q₁ = 40 -Q₁ = 40 – 36 -Q₁ = 4 ∴ Q₁ = -4
अब माध्य = मध्यका = भूयिष्ठक = \(\frac{Q_3+Q_1}{2}\) ∴ µ = \(\frac{36-4}{2}=\frac{32}{2}\) ∴ µ = 16 माध्य = 16

अथवा
Q₁ = µ + 0.6756
36 = µ + 0.675(30)
36 = µ + 20.25
∴ µ = 36 – 20.25
∴ µ = 15.75

प्रश्न 14.
एक प्रामाण्य चल x का माध्य 200 और विचरण100 हो, तो
(i)अंतिम चतुर्थकों की अनुमानित किंमत
(ii) चतुर्थक विचलन की लगभग किंमत
(iii) औसत विचलन की लगभग किंमत ज्ञात कीजिए।
उत्तर :
यहाँ माध्य = µ = 200 और विचरण = δ² = 100 है ∴ δ = 10

(i) अंतिम चतुर्थकों की अनुमानित किंमत Q₁ और Q₃ के लिए निम्न सूत्र का उपयोग करेंगे।
Q₁ = µ – 0.6758 = 200 – 0.675 × 10 = 200 – 6.75 Q₁ = 193.25
Q₃ = µ + 0.6758 = 200 + 0.675 × 10 = 200 + 6.75 Q₃ = 206.75
अंतिम चतुर्थक Q₁ = 193.25 और Q₃ = 206.75 होगा।

(ii) चतुर्थक विचलन की लगभग किंमत
चतुर्थक विचलन = \(\frac {2}{3}\)δ = \(\frac {2}{3}\) × 10 = \(\frac {20}{3}\) ∴ चतुर्थक विचलन = 6.67

(iii) औसत विचलन की लगभग किंमत
औसत विचलन = \(\frac {4}{5}\)δ = \(\frac {4}{5}\) × 10 ∴ औसत विचलन = 8

विभाग – E

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
शहर के एक मोल में ग्राहक द्वारा की गई खरीदी प्रामाण्य वितरण को अनुलक्षित है और उसकी औसत ₹ 800 है, जबकि प्रमाप विचलन ₹ 200 है। यदि यादृच्छिक रीति से किसी एक ग्राहक चयन किया जाया है, तो निम्न घटनाओं की संभावना ज्ञात कीजिए।
(i) उसने की खरीदी की राशि ₹ 850 और ₹ 1200 के बीच हो।
(ii) उसने की खरीदी की राशि ₹ 600 और ₹ 750 के बीच हो।
उत्तरः
यहाँ µ = 800 और δ = 200 दिया है।

(i) ग्राहक द्वारा की गई खरीदी ₹850 और ₹1200 के बीच होने की संभावना

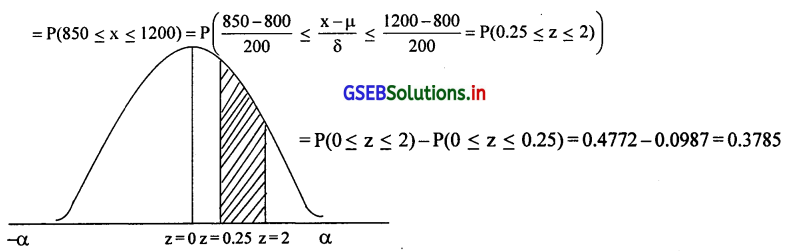
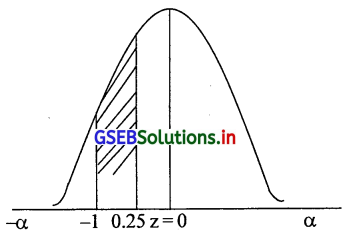
(ii) ग्राहक द्वारा की गई खरीदी की राशि ₹600 और 1750 के बीच होने की संभावना
P(600 ≤ x ≤ 750) P = \(\frac{600-800}{200} \leq \frac{x-\mu}{\delta} \leq \frac{750-800}{200}\) = -1 ≤ z ≤ -0.25)
= P(-1 ≤ z ≤ 0)- P(-0.25 ≤ z ≤ 0)
= (0 ≤ z ≤ 1)- P(0 ≤ z ≤ 0.25)
= 0.3413 – 0.0987 = 0.2426
(1) ग्राहक द्वारा की गई खरीदी की राशि ₹ 850 और ₹ 1200 के बीच होने की संभावना = 0.3785
(2) ग्राहक द्वारा की गई खरीदी की राशि₹ 600 और ₹ 750 के बीच होने की संभावना = 0.2426 है।

प्रश्न 2.
एक विस्तार में निवास करते 20 वर्ष और 26 वर्ष तक आयुवाले 500 व्यक्तियों का औसत वजन 55 कि.ग्रा. और विचरण 100 (कि.ग्रा.) है।व्यक्तियों का वजन प्रामाण्य वितरण को अनुलक्षित है। उसमें से कुछ व्यक्तियों को निम्नानुसार समूह में रखा जाता है।
(i) 70 कि.ग्रा. से अधिक वजनवाले व्यक्तियों को मेदस्वी व्यक्तियों के समूह में रखा गया है।
(ii) 50 कि.ग्रा.और 60 कि.ग्रा. वजनवाले व्यक्तियों को स्वस्थ व्यक्तियों के समूह में रखा जाता है।
(iii) 35 कि.ग्रा.से कम वजनवाले व्यक्तियों को शारीरिक रीति से कमजोर व्यक्तियों के समूह में रखा जाता है।
उपर्युक्त सूचना से उस विस्तार में मेदस्वी, स्वस्थ्य और शारीरिक कमजोर व्यक्तियों की संख्या का अनुमान कीजिए।
उत्तर :
यहाँ N = 500 µ = 55 δ² = 100 δ = 10

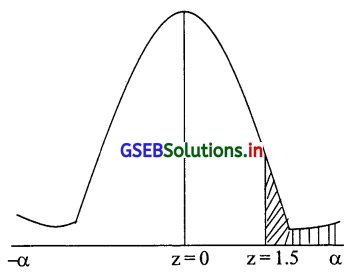
(i) 70 कि.ग्रा. से अधिक वजनवाले व्यक्तियों को मेदस्वी के समूह में रखा जाय तो संभावना
P(x ≥ 70) = P(\(\frac{x-\mu}{\delta} \geq \frac{70-\mu}{\delta}\)) = P = (z ≥ \(\frac{70-55}{10}\)) = P z ≥ 1.5
= P(0 ≤ z ≤ α) – P(0 ≤ z ≤ 1.5)= 0.5 – 0.4332 = 0.0668
70 कि.ग्रा. से अधिक वजनवाले व्यक्तियों की संख्या = N × 0.0668
= 500 × 0.0668 = 33.4 = 33 व्यक्ति लगभग
500 में से 33 व्यक्ति का वजन 70 कि.ग्रा. से अधिक होगा।
मेदस्वी व्यक्ति = 33

(ii) 50 कि.ग्रा.और 60 कि.ग्रा. के बीच वजनवाले व्यक्तियों की संभावना
= P (\(\frac{50-55}{10} \leq \frac{x-\mu}{\delta} \leq \frac{60-55}{10}\)) = P = (\(\frac{-5}{10}\) ≤ z ≤ \(\frac{5}{10}\) = P = (-0.5 ≤ z ≤ 0.5)
= P(-0.5 ≤ z ≤ 0) + P(0 ≤ z ≤ 0.5) = 0.1915 + 0.1915 = 0.3830
50 कि.ग्रा. और 60 कि.ग्रा. के बीच वजनवाले व्यक्तियों की संख्या
= N × 0.3830 = 500 × 0.03830 = 191.5 ≅ 192 व्यक्ति
50 किग्रा. और 60 कि.ग्रा. के बीच वजनवाले व्यक्तियों की संख्या 192 है।
∴ स्वस्थ्य व्यक्ति = 192

(iii) 35 कि.ग्रा.से कम वजनवाले व्यक्तियों की संभावना
= P (x ≤ 35) = P = (\(\frac{x-\mu}{\delta} \leq \frac{35-\mu}{\delta}\)) = P (z ≤ \(\frac{35-55}{10}\)) = P (z ≤ -2)
= P(-α < z ≤ 0)- P(-2 ≤ z ≤ 0)
= 0.5 – 0.4772 = 0.228
35 कि.ग्रा. से कम वजनवाले व्यक्तियों की संख्या = N × 0.0228
= 500 × 0.0228 = 11.4 ≅ 11 व्यक्ति
35 कि.ग्रा. से कम वजनवाली व्यक्तियों की संख्या 11 है।
∴ कमजोर व्यक्ति = 11

प्रश्न 3.
युनिवर्सिटी की एक होस्टेल में निवास करते विद्यार्थियों का औसतमासिक खर्च ₹ 2000 है और उसका प्रमापविचलन ₹ 500 है। यदि विद्यार्थियों का औसत मासिक खर्च का वितरण प्रामाण्य हो, तो
(i) ₹ 750 और ₹ 1250 के बीच खर्च करनेवाले विद्यार्थियों का प्रतिशत ज्ञात कीजिए।
(ii) ₹ 1800 से अधिक खर्च करनेवाले विद्यार्थियों का प्रतिशत ज्ञात कीजिए।
(iii) ₹ 2400 से कम खर्च करनेवाले विद्यार्थियों का प्रतिशत ज्ञात कीजिए।
उत्तरः
औसत मासिक खर्च = µ = 2000 और प्रमाप विचलन = δ = 500

(i) ₹ 750 और ₹ 1250 के बीच खर्च करनेवाले विद्यार्थियों के प्रतिशत की संभावना
P(750 ≤ x ≤1250) P = (\(\frac{750-2000}{500} \leq \frac{x-\mu}{\delta} \leq \frac{1250-2000}{500}\)) = P = (\(\frac{-1250}{500} \leq z \leq \frac{-750}{500}\)) = P (-2.5 ≤ z ≤ -1.5)
= P(-2.5 ≤ z ≤ 0)-P(-1.5 ≤ z ≤ 0) = 0.4938 – 0.4332
= 0.0606
₹ 750 और ₹ 1250 के बीच खर्च करनेवाले विद्यार्थियों के प्रतिशत
= 0.0606 × 100 = 6.06%
6.06% विद्यार्थियों का खर्च ₹ 750 और ₹ 1250 के बीच होगा।

(ii) ₹ 1800 से अधिक खर्च करते विद्यार्थियों के प्रतिशत की संभावना
P(x ≥ 1800) = P(\(\left(\frac{x-\mu}{\delta} \geq \frac{1800-\mu}{\delta}\right)\)) = P(\(\frac{x-\mu}{\delta} \geq \frac{1800-2000}{500}\)) = P (z ≥ – 0.4)
= P(-0.4 ≤ z ≤ 0) + P(0 ≤ z ≤ α ) = 0.1554 + 0.5 = 0.6554
₹1800 से अधिक खर्च करनेवाले विद्यार्थियों के प्रतिशत
= 0.6554 × 100 = 65.54%
65.54% विद्यार्थियों का खर्च ₹1800 से अधिक होगा।

(iii) ₹ 2400 से कम खर्च करनेवाले विद्यार्थियों के प्रतिशत की संभावना
P(x ≤ 2400) = P = (\(\frac{x-\mu}{\delta} \leq \frac{2400-\mu}{\delta}\)) = P = (z ≤ \(\frac{2400-2000}{500}\)) = P (z ≤ \(\frac{400}{500}\)) = P(z ≤ 0.8)
= P(-α < z ≤ 0) + P(0 ≤ z ≤ 0.8) = 0.5 + 0.2881 = 0.7881
₹ 2400 से अधिक खर्च करनेवाले विद्यार्थियों के प्रतिशत
= 0.7881 × 100 = 78.81%
78.81% विद्यार्थियों का खर्च ₹ 2400 से कम होगा।

प्रश्न 4.
एक उत्पादन इकाई में कार्यरत कामदारों काऔसतमासिक वेतन ₹ 10,000 है और उसका प्रमाप विचलन ₹ 2,000 है।कारीगरों का औसत मासिक वेतन प्रामाण्य वितरण को अनुलक्षित है ऐसा मानकर सबं से कम वेतनवाले 20% कामदारों का महत्तम वेतन और सबसे अधिक वेतनवाले 10% कामदारों का लघुतम वेतन का अनुमान कीजिए।
उत्तर :
यहाँ औसत मासिक वेतन ₹ 10,000 है ∴ µ = 10,000 प्रमाप विचलन ₹ 2,000 है ∴ δ = 2,000

(i) सबसे कम वेतन प्राप्त करते 20% कामदारों का महत्तम वेतन की संभावना हो इसलिए कामदारों का वेतन x₁ या उससे कम होने की संभावना = \(\frac{20}{100}\) = 0.20 होगा।
∴ P(x ≤ x₁) = 0.20 ∴ P (\(\frac{x-\mu}{\delta} \leq \frac{x_1-10000}{2000}\)) = 20
∴ P(Z ≤ z₁) = 0.20 जहाँ z₁ = \(\frac{x_1-10000}{2000}\) है।
∴ 0.20 = P(-α < z ≤ 0)- P(z₁ ≤ z ≤ 0)
∴ 0.20 = 0.5-P(z₁ ≤ z ≤ 0)
P(z₁ ≤ z ≤ 0) = 0.5 – 0.2 = 0.3 के लिए तालिका को विलोम
रूप से देखने पर z₁ = -0.84 प्राप्त होगा।
∴ z₁ = \(\frac{x_1-10000}{2000}\)
∴ -0.84 × 2000 = x₁ -10,000
-1680 + 10,000 = x₁
∴ x₁ = 8320 ₹
सबसे कम वेतन प्राप्त करते 20% कामदारों का महत्तम वेतन ₹ 8320 होगा।

(ii) सबसे अधिक वेतनवाले 10% कामदारों का मासिक लघुतम वेतन की संभावना x₁ या उससे अधिक होने की संभावना
x₁ = \(\frac{10}{100}\) = 0.1 P(x ≥ x₁) = 0.1
∴ P(\(\frac{x-\mu}{\delta} \geq \frac{x_1-10000}{2000}\)) = 0.1
P(Z ≥ z₁) = 0.10 जहाँ z₁ = \(\frac{x_1-10000}{2000}\)
∴ 0.10 = P(0 ≤ z < α) – P(0 ≤ z ≤ z₁)
∴ 0.10 = 0.50 -P(0 ≤ Z ≤ z₁)
∴ P(0 ≤ Z ≤ z₁)=0.50 – 0.10 = 0.40
प्रमाणित प्रामाण्य चल की सारणी को विलोम रूप से देखने पर
0.40 के नजदीक z₁ = 1.28 है।
∴ z₁ = \(\frac{x_1-10000}{2000}\)
1.28 = \(\frac{x_1-10000}{2000}\)
= 1.28 × 2000 + 10000 = x₁, 2560 + 10000 = x₁
x₁ = 12560 ₹ सबसे अधिक वेतनवाले 10% कामदारों का मासिक लघुतम वेतन 12560₹ होगा।

प्रश्न 5.
एक प्रामाण्य वितरण का माध्य 52 और विचरण 64 है, तो एकदम बीचोबीचके 25% अवलोकनों को समाविष्ट करती सीमाओं का अनुमान प्राप्त कीजिए।
उत्तर :
यहाँ माध्य μ = 52 और विचरण δ² = 64 ∴ δ = 8
माना कि एकदम बीचोबीच 25% अवलोकन का अंतराल x₁ और x₂ है। x₁ और x₂ माध्य μ से दोनों ओर समान अंतर पर है। x₁ और x₂ के बीच होने की संभावना = \(\frac {25}{100}\) = 0.25 होगा।
अर्थात् P(x₁ ≤ X ≤ x₂) = 0.25 होगा। ∴ P(\(\frac{x_1-\mu}{\delta} \leq \frac{x_1-\mu}{\delta} \leq \frac{x_2-\mu}{\delta}\)) = 0.25
∴ P(z₁ ≤ Z ≤ z₂) = 0.25 जहाँ z₁ = \(\frac{x_1-52}{8}\) और z₂ = \(\frac{x_2-52}{8}\) है
0.25 = P(z₁ ≤ Z ≤ 0) + P(O ≤ Z ≤ z₂)
अब x₁ और x₂ यह माध्य μ से समान अंतर पर होने से z = 0 यह Z = z₁
और Z = z₂ के बीच का क्षेत्रफल के दो समान हिस्सा करता है।
P(z₁ ≤ Z ≤ 0) = 0.125और P(0 ≤ Z ≤ z₂) = 0.125 होगा।
प्रमाणित प्रामाण्य चल की सारणी पर से z₁ = -0.32 और z₂ = 0.32

z₁ = \(\frac{x_1-\mu}{\delta}\)
-0.32 = \(\frac{x_1-52}{8}\)
-0.32 × 8 = x₁ – 52
2.56 + 52 = x₁
x₁ = 49.44 ∴ x₁ = 49.44

z₂ = \(\frac{x_2-\mu}{\delta}\)
-0.32 = \(\frac{x_2-52}{8}\)
0.32 × 8 = x₂ – 52
-2.56 + 52 = x₂
x₂ = 54.56 ∴ x₂ = 54.56
एकदमबीचो बीच आनेवाले 25% अवलोकन का अंतराल 49.44 से 54.56 होगा।

प्रश्न 6.
इलेक्ट्रोनिक्स उपकरण के एक बड़े शोरुम में प्रति सप्ताह औसत 52 उपकरण बिक्री होते है और उसका विचरण 9 (इकाई)² है। इलेक्ट्रोनिक्स उपकरणों की बिक्री प्रामाण्य वितरण को अनुलक्षित है, ऐसा माना जाता है। 50 सप्ताह में से किसी एक सप्ताह दौरान उपकरण की बिक्री x₁ इकाई और 61 इकाई के बीच हुआ हो उसकी संभावना 0.1574 हो, तो x₁ का मूल्य और कितने सप्ताहदौरान
उपकरणों की बिक्री 55 इकाई से अधिक होगी उसका अनुमान ज्ञात कीजिए।
उत्तर :
औसत बिक्री 52 है ∴ μ = 52 विचरण δ² = 9 है ∴ δ = 3

(i) किसी एक सप्ताह दौरान उपकरण की बिक्री x₁ इकाई और 61 इकाई होने की संभावना 0.1574 है। x₁ और x₂ के बीच होने की संभावना 0.1574 होगा अर्थात् P(x₁ ≤ X ≤ x₂) = 0.1574
∴ P(\(\frac{x_1-\mu}{\delta} \leq \frac{x-\mu}{\delta} \leq \frac{x_2-\mu}{\delta}\)) = 0.1574
∴ P(Z₁ ≤ Z ≤ Z₂) = 0.1574 जहाँ z₁ = \(\frac{x_1-52}{3}\) और z₂ = \(\frac{x_2-52}{3}\) होगा
z₂ = \(\frac{61-52}{3}\) > z₂ = \(\frac{9}{3}\) ∴ z₂ = 3
Z₂ = 3 के लिए तालिका पर से z₂ का क्षेत्रफल 0.4987 प्राप्त होगा।
0.1574 = P(0 ≤ Z ≤ z₂) – P(0 ≤ Z ≤ z₁)
0.1574 = 0.4987 – P(0 ≤ Z ≤ z)
∴ P(0 ≤ Z ≤ z₁) = 4987 – 0.1574 = 0.3413 के लिए z₁ का मूल्य प्रामाण्य वितरण की तालिका को विलोम रूप से देखने पर z₁ = 1 प्राप्त होगा।
अब,z₁ = \(\frac{x_1-52}{3}\) 1 = \(\frac{x_1-52}{3}\)
1 × 3 + 52 = x ∴ x₁ = 55

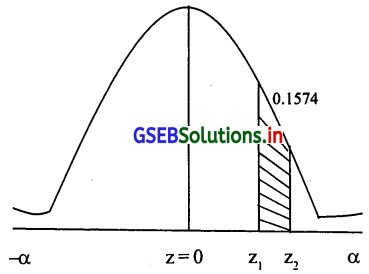
(ii) कितने सप्ताह में उपकरणों की बिक्री 55 इकाई से अधिक होगी उसकी संभावना
P(x ≥ 55) = P(\(\frac{x-\mu}{\delta} \geq \frac{55-\mu}{\delta}\)) = P(\(\frac{x-\mu}{\delta} \geq \frac{55-52}{3}\)) ∴ P(Z ≥ 1)
= P(0 ≤ Z ≤ α) – P(0 ≤ Z ≤ 1)= 0.5 – 0.3413 = 0.1587
55 इकाई से अधिक बिक्रीवाले सप्ताह की संख्या
= N × 0.1587 = 50 × 0.1587 = 7.935
≅ 8 सप्ताह
55 इकाई से अधिक बिक्रीवाले 8 सप्ताह होंगे।

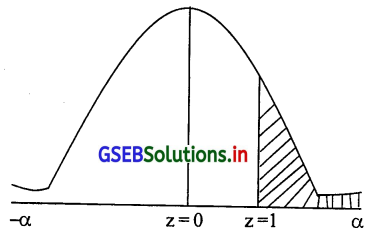
प्रश्न 7.
पेन्टींग प्रदर्शनी में आनेवाली व्यक्ति औसत 61 मिनिट का समय व्यतीत करता है।यहसमय प्रामाण्य रीति से वितरित हो और 20% व्यक्ति प्रदर्शनी में 30 मिनिट से कम समय व्यतीत करते हो, तो वितरण का विचरण ज्ञात कीजिए । एवं किसी व्यक्ति 90 मिनिट से अधिक समय प्रदर्शनी में व्यतीत करे तो उसकी संभावना ज्ञात कीजिए।
उत्तर :
औसत समय = μ = 61 दिया है।
20% व्यक्ति प्रदर्शन में 30 मिनिट से कम समय व्यतीत करता हो उसकी संभावना = \(\frac {20}{100}\) = 0.2 और x₁ = 30 है अर्थात् P(x ≤ 30)= 0.2
P(x < x₁)= 0.20 ∴ P(\(\frac{x-\mu}{\delta} \leq \frac{x_1-61}{\delta}\)) = ∴ P = (\(\frac{x-\mu}{\delta} \leq \frac{30-61}{8}\)) = 0.20 P(\(\frac{x-\mu}{\delta} \leq \frac{-31}{8}\)) = 0.20
∴ P(Z ≤ Z₁) = 0.20 जहाँ z₁ = \(\frac{-31}{8}\) ∴ P(z < z₁) = 0.20 जहाँ z₁ = \(\frac{-31}{8}\)
∴ 0.20 = P(-α < Z ≤ 0) – P(z₁ ≤ Z ≤ 0)
0.20 = 0.5- P(z₁ ≤ z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0) = 0.5-0.20 = 0.30 क्षेत्रफल के लिए प्रामाण्य वक्र की तालिका को विलोम रूप से देखने पर z₁ = -0.84 प्राप्त होगा।
z₁ = -0.84 z₁ = \(\frac{-31}{8}\) -0.84 × δ = 31
∴ δ = \(\frac{-31}{-0.84}\) ∴ δ = 36.909 ∴ δ² = 1362.25
विचरण = 1362.25

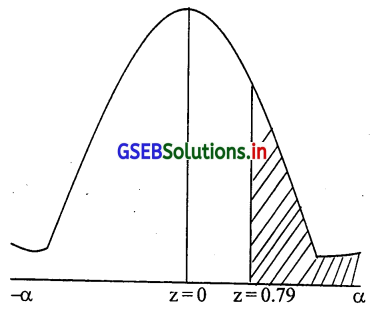
किसी व्यक्ति 90 मिनिट से अधिक समय प्रदर्शनी में रूके उसकी संभावना P(x ≥ 90)
P(x ≥ 90) = P(\(\frac{x-\mu}{\delta} \geq \frac{90-61}{36.909}\)) = P(Z ≥ \(\frac{29}{36.909}\)) = P(Z ≥ 0.7857) = P(Z ≥ 0.79)
∴ P(0 ≤ Z ≤ α) – P(0 ≤ Z ≤ 0.79)
∴ 0.5 – 0.2852
∴ 0.2148
P(x ≥ 90) की संभावना = 0.2148
90 मिनिट से अधिक समय प्रदर्शन में व्यतीत करे उसकी संभावना = 0.2148 होगा।

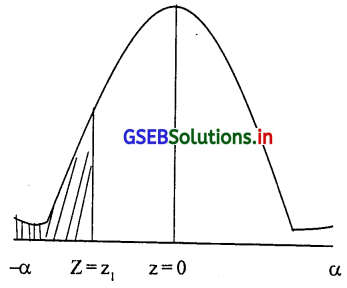
प्रश्न 8.
पाईप बनानेवाली एक उत्पादक कंपनी में उत्पादित होती पाईप का व्यास 20 मि.मि. से 22 मि.मि. का हो, तो वह किसी एक निश्चित समूह के ग्राहक द्वारा स्वीकार्य है। उत्पादित हुई पाईप का व्यास का प्रमाप विचलन 4 मि.मि. है और उत्पादित होती 70% पाईप का व्यास 19.05 मिमि से अधिक हो, तो उत्पादित होनेवाली पाईपका व्यास का माध्य ज्ञात कीजिए एवं कंपनी द्वारा उत्पादित हुई पाईप का निश्चित समूह के ग्राहक द्वारा अस्वीकार्य पाईप का प्रतिशत भी ज्ञात कीजिए।
नोट : यहाँ उत्पादित पाईप का व्यास प्रामाण्य वितरण को अनुलक्षित है।
उत्तर :
यहाँ प्रमाप विचलन = δ = 4 उत्पादित हुई 70% पाईप का व्यास 19.05 मिमि से अधिक होने की संभावना
∴ P(x ≥ 19.05)= 0.7 ∴ p(\(\frac{x-\mu}{\delta} \geq \frac{x_1-\mu}{4}\)) = 0.7 यहाँ P(Z ≥ Z₁) = 0.7 जहाँ z₁ = \(\frac{19.05-\mu}{4}\)
∴ 0.7 = P(z₁ ≤ Z ≤ 0) + P(0 ≤ Z ≤ a)
∴ 0.7 = P(z₁ ≤ Z ≤ 0) + 0.5
∴ 0.7 – 0.5 = P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0) = 0.2 प्रमाणित प्रामाण्य की सारणी को विलोम रूप से देखने पर z₁ = -0.525 प्राप्त होगा।
अब z₁ = \(\frac{x_1-\mu}{\delta}\) -0.525 = \(\frac{19.05-\mu}{4}\)
-0.525 × 4 = 19.05 – μ
-2.1 + μ = 19.05 ∴ μ = 19.05 + 2.1 ∴ μ = 21.15
माध्य = 21.15 होगा।

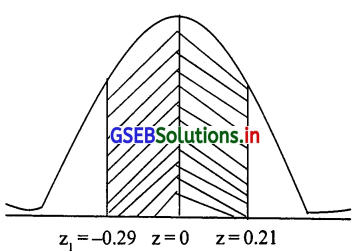
अब 20 मिमि और 22 मिमि व्यास को स्वीकार्य माना जाय तो स्वीकार्य व्यास की संभावना
∴ P(20 ≤ x ≤ 22) = P(\(\frac{20-21.15}{4} \leq \frac{x-\mu}{\delta} \leq \frac{22-21.15}{4}\))
= P(-0.2875 ≤ Z ≤ 0.2125) = P(-0.29 ≤ Z ≤ 0.21)
= P (-0.29 ≤ Z ≤ 0)+ P(0 ≤ Z ≤ 0.21)
= 0.1141 + 0.0832
स्वीकार्य पाईप = 0.1973
∴ अस्वीकार्य पाईप = 1 – 0.1973 = 0.8027 संभावना
अस्वीकार्य पाईप के प्रतिशत = 0.8027 × 100 = 80.27%
अस्वीकार्य पाईप के प्रतिशत 80.27% होगा।

प्रश्न 9.
एक प्रामाण्य चल X का माध्य 400 और विचरण 900 प्राप्त होता है, तो इस वितरण का चौथा दशांशक और 90वां शतमक ज्ञात करके उसका अर्थघटन कीजिए।
उत्तर :
यहाँ µ = 400 δ² = 900 ∴ δ = 30
दी गई सूचना का चतुर्थ दशमक (D₄) ज्ञात करना है। अब D₄ की परिभाषा अनुसार सूचना के 40% अवलोकन का मूल्य D₄ जीतना या उससे कम होगा।
∴ P(x ≤ D₄) = \(\frac {40}{100}\)
∴ P(\(\frac{x-\mu}{\delta} \leq \frac{D_4-400}{30}\)) = 0.40 ∴ P(z < z₁)- 0.40 जहाँ z₁ = \(\frac{D_4-400}{30}\) है।
0.40 = P( -α < z ≤ 0)- P(z₁ ≤ Z ≤ 0)
0.4 = 0.5 – P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ z ≤ 0) = 0.5 – 0.4 = 0.1
प्रमाणित प्रामाण्य चल की सारणी पर से z₁ का मूल्य

∴ z₁ = -0.255
∴ -0.255 = \(\frac{\mathrm{D}_4-400}{30}\)
-0.255 × 30 + 400 = D₄
-7.65 + 400 = D₄
∴ D₄ = 392.35
चतुर्थ दशमक = 392.35.

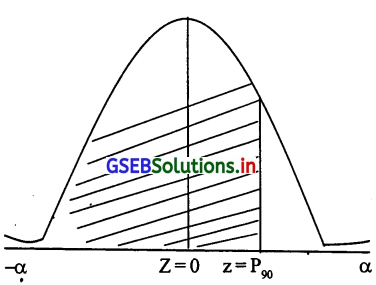
अब 90वां शतमक (P₉₀) की परिभाषा पर से सूचना के 90% अवलोकन या उससे कम होगा।
∴ P(x ≤ P₉₀) = \(\frac{90}{100}\)
P(\(\frac{x-\mu}{\delta} \leq \frac{P_{90}-400}{30}\)) = 0.9 ∴ P(z ≤ z₁) = 0.9 जहाँ z₁ = \(\frac{P_{90}-400}{30}\) है।
0.90 = P(-α < z ≤ 0) + P(0 ≤ Z ≤ z₁)
0.90 = 0.50 + P(0 ≤ Z ≤ z₁)
0.90 – 0.50 = P(0 ≤ z ≤ z₁)
∴ P(0 ≤ z ≤ z₁)= 0.40
प्रमाणित प्रामाण्य चल की सारणी पर से z, का अंदाजित मूल्य कोष्टक को विलोम रूप से देखने पर z₁ = 1.28
∴ z₁ = \(\frac{x_1-400}{30}\) 1.28 x 30 + 400 = 90
∴ P₉₀ = 400 + 38.4 = 438.4
90 वां शतमक का मूल्य 438.4 होगा
∴ P = 438.4

प्रश्न 10.
एक प्रामाण्य चल x का संभावना-वितरण घटत्व फलन निम्नानुसार है।
f(x) = \(\frac{1}{50 \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-150}{50}\right)^2}\);-α < x < α
इस वितरण के लिए
(i) P(x₁ ≤ x ≤ 250) = 0.4772 हो, तो x₁ का मूल्य का अनुमान
(ii) P(75 < x < x₂) = 0.3539 हो, तो x₂ का मूल्य का अनुमान ज्ञात कीजिए।
उत्तर :
दिया गया संभावना घटत्व फलन को प्रामाण्य चल x का संभावना घटत्व फलन के साथ तुलना करने पर
f(x) = \(\frac{1}{\delta \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{3}\right)^2}\):-α < x < α
∴ µ = 150 और δ = 50

(i) P(x₁ ≤ x ≤ 250) = 0.4772 ∴ P(x₁ ≤ x ≤ x₂) = 0.4772
∴ P(\(\frac{x_1-150}{50} \leq \frac{x-\mu}{\delta} \leq \frac{250-150}{50}\)) = 0.4772
P(\(\frac{x_1-150}{50}\) ≤ z ≤ 2)- 0.4772
0.4772 = Z₂ = 2
0.4772 – 0.4772 = Z₁
∴ Z₁ = 0
0.4772 = P(z₁ ≤ z ≤ z₂) ∴ Z₁ = 0
z₁ = \(\frac{x_1-\mu}{\delta}\)
0 = \(\frac{x_1-150}{50}\) 0 × 50 + 150 = x₁
∴ x₁ = 150

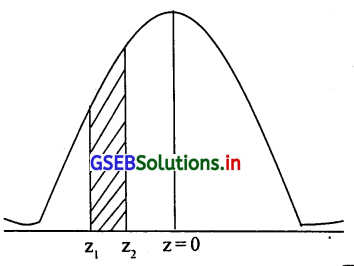
(ii) P(75 < x < x₂) = 0.3539 हो, तो x₂ का मूल्य ∴ P(x₁ ≤ x ≤ x₂) = 0.3539
∴ P(\(\frac{75-150}{50}\) ≤ z ≤ \(\frac{x_2-150}{50}\)) = 0.3539 ∴P(-1.5 ≤ z ≤ \(\frac{x_2-150}{50}\) = 0.3539
Z₁ = -1.5 के लिए संभावना = 0.4332
= P(z₁ ≤ z ≤ 0) – P(z₂ ≤ z ≤ 2) = P(z₂ ≤ z ≤ 0)
= 0.4332 – 0.3539 = P(z₂ ≤ z ≤ 0)
= 0.0793 क्षेत्रफल के लिए z₂ का मूल्य तालिका को विलोम रूप से देखने पर z₂ = -0.2 प्राप्त होगा।
z₂ = \(\frac{x_2-\mu}{\delta}\) -0.2 = \(\frac{x_2-150}{50}\) – 0.2 × 50 = x₂ – 150
∴ -10 + 150 = x₂
∴ x₂ =140

विभाग – F

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
500 बालकों की एक बौद्धिक परीक्षा के औसत नंबर 68 और प्रमापविचलन 22 मिला, यदिबालकों द्वारा प्राप्त नंबर प्रामाण्य रीति से वितरीत हो, तो
(1) 68 से अधिक नंबर प्राप्त करते बालकों की संख्या ज्ञात करो।
(2) 70 और 90 के बीचनंबर प्राप्त करते बालकों की प्रतिशतता ज्ञात करो।
(3) सबसे अधिक नंबर प्राप्त करते 50 बालकों का कम से कम नंबर ज्ञात कीजिए।
उत्तर :
N = 500, माध्य = μ = 68 प्रमाप विचलन = δ = 22
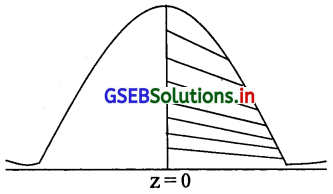
(1) 68 से अधिक नंबर प्राप्त करते बालकों की संभावना = P(x ≥ 68) = P(\(\frac{x-\mu}{\delta}\) ≥ \(\frac{68-68}{22}\)) = P(z ≥ 0)
∴ P(0 ≤ z ≤ α) = 0.5
P(x ≥ 68) की संभावना = 0.5
बालकों की संख्या = N × 0.5 = 500 × 0.5 = 250
68 से अधिक नंबर प्राप्त करते बालकों की संख्या 250 होगी।

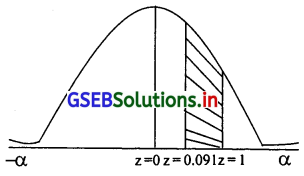
(2) 70 और 90 के बीच नंबर प्राप्त करते बालकों की संभावना = P(\(\frac{70-68}{22} \leq \frac{x-\mu}{\delta} \leq \frac{90-68}{22}\)) = P(0.091 ≤ 2 ≤ 1)
= P(0 ≤ z ≤ 1) – P(0 ≤ z ≤ 0.091) = 0.3413 – 0.0359 = 0.3054
70 और 90 के बीच नंबर प्राप्त करते बालकों के प्रतिशत
= 0.3054 × 100 = 30.54%
70 और 90 के बीच 30.54% बालकों के नंबर होंगे।

(3) सबसे अधिक नंबर प्राप्त करनेवाले 20 बालकों की संभावना = \(\frac {50}{100}\) = 0.1 होगी।
= P(x ≥ x₁)= 0.1 ∴ P(\(\frac{x-\mu}{\delta} \geq \frac{x_1-68}{22}\)) = 0.1
यहाँ P(Z ≥ z₁) = 0.1 जहाँ = z₁= \(\frac{x_1-68}{22}\)
∴ 0.1 = P(0< z ≤ α)-P(0 ≤ Z ≤ z₁)
∴ 0.1 = 0.5 – P(0 ≤ Z ≤ z₁)
∴ P(0 ≤ Z ≤ z₁) = 0.5 – 0.1
= 0.4 प्रमाणित प्रमाण्य वितरण की तालिका को विलोम रूप से देखने पर z₁ = 1.28 प्राप्त होगा।
z₁ = \(\frac{x_1-68}{22}\) 1.28 x 22 = x₁ – 68 28.16 + 68 = x₁
∴ x₁ = 96.16 ≅ 96 नंबर
50 बालकों के कम से कम नंबर 96 होगा।

प्रश्न 2.
एक निजी कंपनी में कार्यरत 500 कर्मचारियों की उम्र का वितरण प्रामाण्य है। उसका माध्य 40 वर्ष और प्रमाप-विचलन वर्ष है। कंपनी निम्न कक्षा के अनुसार 25% कर्मचारियों का निष्कासन करना चाहती है।
(i) सबसे कम उम्रवाले 5% कर्मचारियों का निष्कासन करना।
(ii) कम उम्रवाले 5% कर्मचारियों का निष्कासनकरनाऔर 10% से कम उम्रवाले कर्मचारियों का अन्यकंपनी में बदली करना।
(iii) सबसे अधिक उम्रवाले 10% कर्मचारियों को निवृत्त करना।
इस सूचना से निष्कासन कर्मचारी अन्य कंपनी में बदली होते कर्मचारी और निवृत्त होते कर्मचारियों की अनुमानित उम्र ज्ञात कीजिए।
उत्तर :
यहा N = 500, माध्य = µ = 40, प्रमाप विचलन = δ = 6
(i) सबसे कम उम्रवाले 5% कर्मचारियों का निष्कासन करना हो तो संभावना = \(\frac {5}{100}\) = 0.05

P(x ≤ x₁) = 0.05 P(\(\frac{x-\mu}{\delta} \leq \frac{x_1-40}{6}\)) = 0.05 P( Z ≤ \(\)) = 0.05
यहाँ P(Z ≤ z₁) = 0.05 जहाँ z₁ = \(\frac{x_1-40}{6}\)
∴ 0.05 = P(-α < z ≤ 0) – P(z₁ ≤ Z < 0)
∴ 0.05 = 0.5 – P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0) = 0.5 – 0.05
= 0.45 प्रमाणित प्रामाण्य वितरण की तालिका को विलोम रूप से देखने पर
z₁ = -1.645 प्राप्त होगा।
z₁ = \(\frac{x_1-40}{6}\) -1.645 × 6 = x₁ -40 -9.89 + 40 = x₁
x₁ = 30.13 वर्ष
सब से कम उम्रवाले 5% कर्मचारी की उम्र 30.13 वर्ष होगी।

(ii) कम उम्र के 5% कर्मचारियों को निष्कासन करना है और 10% कम उम्रवाले को अन्य कंपनी में बदली करना हो तो उम्र की संभावना \(\frac{5}{100}+\frac{10}{100}=\frac{15}{100}\) = 0. 15
0.15 = P(-α < z ≤ 0)- P(z₁ ≤ z ≤ 0)
∴ 0.15 = 0.5- P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0)= 0.5 – 0.15
= 0.35 क्षेत्रफल के लिए प्रामाण्य वितरण की तालिका को विलोम रूप से देखने पर z₁ = -1.033 प्राप्त होगा।
z₁ = \(\frac{x_1-\mu}{\delta}\) -1.035 = \(\frac{x_1-40}{6}\) -1.035 × 6 = x₁ – 40
-6.21 + 40 = x₁ x₁ = 33.79 वर्ष
33.79 वर्ष से कम उम्रवाले का स्थानांतरण अन्य कंपनी में किया जायेगा।

(iii) सबसे अधिक उम्रवाले 10% कर्मचारियों को निवृत्त करना हो तो उसकी संभावना = \(\frac {10}{100}\) = 0.1
∴ P(x ≥ x₁) = 0.1 ∴ P(\(\frac{x-\mu}{\delta} \geq \frac{x_1-40}{6}\)) = 0.1 यहाँ P(Z ≥ z₁) = 0.1 जहाँ z₁ = \(\frac{x_1-40}{6}\)
∴ 0.1 = P(0 ≤ z ≤ α ) – P(0 ≤ Z ≤ z₁)
∴ 0.1 = 0.5 – P(0 ≤ Z ≤ z₁)
∴ P(0 ≤ Z ≤ z₁)= 0.5 – 0.1
∴ P(0 ≤ Z ≤ z₁) = 0.4 क्षेत्रफल के लिए प्रामाण्य वितरण की तालिका को विलोम रूप से देखने पर z₁ = 1.28 प्राप्त होगा।
z₁ = \(\frac{x_1-\mu}{\delta}\) 1.28 = \(\frac{x_1-40}{6}\) 1.28 × 6 = x₁ – 40
7.68 + 40 = x₁ ∴ x₁ = 47.68 वर्ष
सबसे अधिक उम्रवाले 10% कर्मचारियों को निवृत्त करना हो तो उम्र 47.68 वर्ष

प्रश्न 3.
उच्च अभ्यास में प्रवेश हेतु 200 अंक की परीक्षा ली जाती है। इस परीक्षा में उपस्थित 20,000 विद्यार्थियों द्वारा प्राप्त अंक प्रामाण्य वितरण के अनुलक्षित है और उसका माध्य 120 अंक और प्रमाणित विचलन 20 अंक है। परिणाम के मापदंड निम्नानुसार है:
(a) 40% से कम अंक प्राप्त करनेवाले विद्यार्थी अनुत्तिर्ण होते है।
(b) 40% से 48% अंक प्राप्त विद्यार्थियों की एक 100 अंक की दूसरी परीक्षा ली जाती है।
(c) 48% से 75% अंक प्राप्त विद्यार्थियों को साक्षात्कार के लिए बुलाया जाता है।
(d) 75% से अधिक अंक प्राप्त विद्यार्थियों को उच्च अभ्यास में प्रत्यक्ष प्रवेश दिया जाता है। तो
(1) अनुत्तीर्ण होते
(2) 100 अंक की परीक्षा देनेवाले
(3) साक्षात्कार में आनेवाले
(4) उच्च अभ्यास में प्रत्यक्ष प्रवेशपात्र विद्यार्थियों की लगभग संख्या ज्ञात कीजिए।
उत्तर :
यहाँ N = 20,000, माध्य = µ = 120, प्रमाप विचलन = δ = 20
(a) 40% से कम अंक प्राप्त करनेवाले अनुत्तीर्ण होते है अर्थात् 200 अंक में से \(\frac{200 \times 40}{100}\) = 80 से कम अंकवाले अनुत्तीर्ण होंगे।’
∴ x₁ = 80
∴ P(\(\frac{x-\mu}{\delta} \leq \frac{\delta 0-120}{20}\)) = p(Z ≤ \(\frac{-40}{20}\)) ∴ P(Z ≤ 2)
= P(-α < z ≤ 0) – P(-2 ≤ Z ≤ 0)
= 0.5 – 0.4772 = 0.0228
40% से कम अंक अर्थात् 200 में से 80 से कम अंक प्राप्त करनेवाले अनुत्तीर्ण होंगे उसकी संभावना = 0.0228 होगा।
∴ अनुत्तीर्ण होनेवाले विद्यार्थियों की संख्या = N × 0.0228
= 20,000 × 0.0228 = 456,
456 विद्यार्थी अनुत्तीर्ण होंगे।

(b) 40% और 48% अर्थात् 200 में से 40% = 80 अंक। 48% = 96 अंक। 80 और 96 के बीच अंक प्राप्त करनेवालों की 100 अंक की परीक्षा ली जाती है तो 100 अंक की परीक्षा देनेवाले की संभावना
P(80 ≤ x ≤ 96) = P(\(\frac{80-120}{20} \leq \frac{x-\mu}{\delta} \leq \frac{96-120}{20}\)) = P(-2 ≤ Z ≤ -1.2)
= P (-2 ≤ Z ≤ 0) – P(-1.2 ≤ Z ≤ 0)
= 0.4772 – 0.3849 = 0.0923
100 अंक की परीक्षा देनेवाले विद्यार्थियों की संख्या = N × 0.0923
= 0.0923 × 20,000 = 1846
1846 विद्यार्थियों को 100 अंक की परीक्षा देनी पड़ेगी।

(c) 48% और 75% अंक प्राप्त विद्यार्थियों को साक्षात्कार में बुलाया जाता है अर्थात् 200 में से 48% = 96 अंक और 75% अर्थात् 150
अंक 96 और 150 अंक प्राप्त करनेवाले विद्यार्थियों की संभावना
P(96 ≤ x ≤ 150) = P(\(\frac{96-120}{20} \leq \frac{x-\mu}{\delta} \leq \frac{150-120}{20}\)) = P(-1.2 ≤ Z ≤ 1.5)
= P (-1.2 ≤ Z ≤ 0) + P(0 ≤ Z ≤ 1.5)
= 0.3849 + 0.4332 = 0.8181
साक्षात्कार में बुलाया गया विद्यार्थियों की संख्या = N × 0.8181
= 20,000 × 0.8181 = 16362
16362 विद्यार्थियों को साक्षात्कार में बुलाया जायेगा।

(d) 75% से अधिक अंक प्राप्त करनेवाले को उच्च अभ्यास में सीधा प्रवेश दिया जायेगा अर्थात् 200 में से 150 अंक प्राप्त करनेवाले को सीधा प्रवेश दिया जायेगा उसकी संभावना
p(x ≥ 150) = P(\(\frac{x-\mu}{\delta} \geq \frac{150-120}{20}\)) = P(Z ≥ 1.5)
= P (0 ≤ z ≤ a) – P(0 ≤ Z ≤ 1.5)
= 0.5 – 0.4332 = 0.0668
उच्च अभ्यास में सीधा प्रवेश पात्र विद्यार्थियों की संख्या
= 0.0668 × 20,000 = 1336
1336 विद्यार्थियों को उच्च अभ्यास में प्रवेश दिया जायेगा।

प्रश्न 4.
एक समूह के व्यक्तियों का मासिक आय का वितरण प्रामाण्य वितरण का अनुलक्षित है और उसका माध्य ₹ 20,000 और प्रमाप विचलन ₹ 5,000 है।यदि सबसे अधिक आयवाले 50 व्यक्तियों की कम से कम मासिक आय ₹ 31,625 हो, तो समूहमें कुल कितनी व्यक्ति होगी? समूह में सबसे कम आयवाले 50 व्यक्तियों की अधिक से अधिक आय कितनी होगी?(गणना में दशमलव के चिह्न के बाद दो अंको का उपयोग कीजिए।
उत्तर :
यहाँ माध्य = µ = 20,000, प्रमाप विचलन = δ = 5,000, सबसे अधिक आयवाले 50 व्यक्तियों की कम से कम मासिक आय ₹ 31,625 हो, तो x₁ = 31,625 के अनुरूप z₁ का मूल्य
Z₁ = \(\frac{31625-20000}{5000}=\frac{11625}{5000}\) = 2.325 Z₁ = 2.33
= P (0 ≤ Z ≤ α) – P(0 ≤ Z ≤ z₁)
= P(0 ≤ Z ≤ α ) – P(0 ≤ Z ≤ 2.33)
= 0.5 – 0.4901 = 0.0099
समूह में कुल व्यक्तियों की संख्या N है। अब ₹ 31,625 से अधिक आयवाले व्यक्तियों की संख्या 50 है। अत: संभावना की परिभाषा के अनुसार
31,625 से अधिक आयवाले व्यक्तियों की संभावना 0.0099 है।

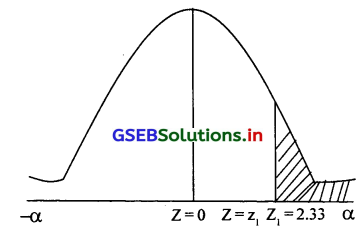
P(x ≥ 31625) = P(Z ≥ 2.33)= \(\frac{50}{N}\) अब \(\frac{50}{N}\) = 0.0099
∴ N = \(\frac{50}{0.0099}\) = 5050.51 N ≅ 5051 व्यक्ति समूह में कुल 5051 व्यक्ति होंगे।

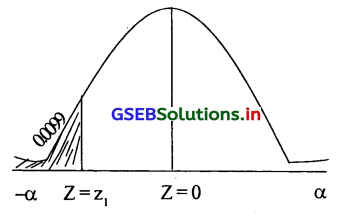
समूह में सबसे कम आयवाले 50 व्यक्तियों की अधिक से अधिक आय कितनी होगी? 50 व्यक्तियों का क्षेत्रफल = \(\frac{50}{5051}\) = 0.0099 उर्ध्वसीमा ज्ञात करना है इसलिए क्षेत्रफल बायी ओर वक्र में दर्शायेंगे।
= P(-α < Z ≤ 0) – P(z₁ ≤ Z ≤ 0)
0.0099 = 0.5 – P(z₁ ≤ Z ≤ 0)
P(z₁ ≤ Z ≤ 0) = 0.5 – 0.0099 = 0.4901
क्षेत्रफल के लिए प्रामाण्य वक्र की तालिका को विलोम रूप से देखने पर
Z₁ = -2.33 प्राप्त होगा।
z₁ = \(\frac{x_1-\mu}{\delta}\) -2.33 = \(\frac{x_1-20,000}{5,000}\) -2.33 x 5000 = x₁ – 20,000
-11,650 + 20,000 = x₁ ∴ x₁ = 8,350
सबसे कम आयवाले 50 व्यक्तियों की मासिक आय उर्ध्वसीमा (अधिक से अधिक) ₹ 8,350 होगी।

प्रश्न 5.
एक विद्यालय के कक्षा 12वीं का परिणाम का विश्लेषण निम्नानुसार प्राप्त किया है:
विशिष्ट गुणवत्ता के साथ उत्तीर्ण : कुल विद्यार्थियों का 15%
विशिष्ट गुणवत्ता के बिना उत्तीर्ण : कुल विद्यार्थियों का 75%
अनुत्तीर्ण :कुल विद्यार्थियों का 10%
उत्तिर्ण होने के लिए कम से कम 40% गुणऔर विशिष्टगुणवत्ता के लिए कम से कम 80% गुण आवश्यक है।यदि विद्यार्थियों द्वारा प्राप्त परिणाम प्रामाण्य वितरणको अनुलक्षित हो तो सूचनाकामाध्य (µ) और प्रमापविचलन (δ) प्राप्त कीजिए और उसका उपयोग करके 75% विद्यार्थियों का परिणाम कितने प्रतिशत से कम होगा वह ज्ञात कीजिए।
उत्तर :
माना कि 100 अंक की परीक्षा हुई है। उत्तीर्ण होने के लिए कम से कम 40% अर्थात् 40 से कम अंक प्राप्त करनेवाले अनुत्तीर्ण होंगे
P(x ≤ 40) और विशिष्ट गुणवत्ता के लिए कम से कम 80% अर्थात् 80 से अधिक अंक प्राप्त करनेवाले विशिष्ट गुणवत्ता के साथ उत्तीर्ण होंगे अर्थात् P(x ≥ 80)

प्रामाण्य वितरण का माध्य µ और प्रमाप विचलन δ है। 40 से कम अंक प्राप्त करनेवाले की संभावना
= P(x ≤ 40) = P(\(\frac{x_1-\mu}{\delta} \leq \frac{40-\mu}{\delta}\)) = P(Z ≤ \(\frac{40-\mu}{\delta}\)) = कुल विद्यार्थियों के 10% अनुत्तीर्ण होते है इसलिए उसकी संभावना = \(\frac{10}{100}\) = 0.1
∴ P(Z ≤ \(\frac{40-\mu}{\delta}\) = 0.1 ∴ P(z₁ < z₁)= 0.10 जहाँ z₁ = \(\frac{40-\mu}{\delta}\)
∴ 0.1 = P(-α < Z ≤ 0) – P(z₁ ≤ Z ≤ 0)
∴ 0.10.5 – P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0)= 0.5 – 0.1 = 0.4
क्षेत्रफल के लिए प्रामाण्य चल की सारणी को विलोम रूप से देखने पर
z₁ = -1.28 4
z₁ = \(\frac{x_1-\mu}{\delta}\) -1.28 = \(\frac{40-\mu}{\delta}\) -1.28δ = 40 – µ …………….(i)
विशिष्ट गुणवत्ता के साथ उत्तीर्ण विद्यार्थी कुल विद्यार्थी के 15% है। इसलिए
विशिष्ट गुणवत्ता के अंक x₁ या उससे अधिक होने की संभावना = 0.15
∴ P (x ≥ 80) = 0.15

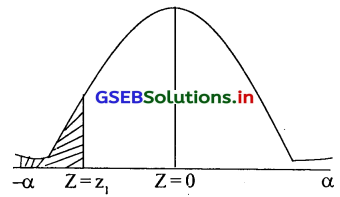
∴ P(\(\frac{x-\mu}{\delta} \geq \frac{80-\mu}{\delta}\)) ∴ P(Z ≥ z₁) = 0.15 जहाँ z₁ = \(\frac{80-\mu}{\delta}\)
∴ 0.15 = P(0 ≤ Z ≤ α) – P(0 ≤ Z ≤ z₁)
∴ 0.15 = 0.5 – P(0 ≤ Z ≤ z₁)
∴ P(O ≤ Z ≤ z₁) = 0.5 – 0.15 = 0.35
क्षेत्रफल के लिए प्रमाणित प्रामाण्य चल की सारणी को विलोम रूप से देखने पर Z₁ = 1.035 प्राप्त होगा। .
∴ z₁ = \(\frac{x_1-\mu}{\delta}\) 1.035 = \(\frac{80-\mu}{\delta}\) = 1.035δ = 80 – µ …………….(ii)
परिणाम (i) और (ii) की तुलना करने पर

∴ δ = \(\frac{-40}{-2.315}\) ∴ δ = 17.28 प्र.वि. = 17.28
अब परिणाम (i) में δ = 17.28 रखने पर – 1.28 (17.28) = 40 – µ -22.12 + µ = 40 ∴ µ = 40 + 22.12
∴ µ = 62.12 माध्य = 62.12
75% विद्यार्थी के परिणाम कितने प्रतिशत से कम होंगे यहाँ 75% से कम अर्थात् P₇₅ = Q₃ ज्ञात होगा।
Q₃ = µ + 0.675δ = 62.12 + 0.675 (17.28) = 62.12 + 11.66 = 73.78, 75% विद्यार्थी के परिणाम 73.78 से कम होगा

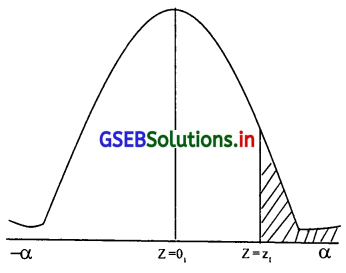
प्रश्न 6.
एक प्रोविजन स्टॉर्स के स्थायी ग्राहकों के बिल की राशि प्रामाण्य वितरणको अनुलक्षित है।यदि 7.78% स्थायी ग्राहकों का मासिक बिल ₹ 3,590 से कम हो,और 94.52% ग्राहकों का मासिक बिल की राशि ₹ 5100 से कम हो, तो प्रामाण्य वितरण के प्राचल ज्ञात कीजिए। एवं एकदम बीच के 95% ग्राहकों के मासिक बिल की रशि का अनुमान ज्ञात कीजिए।
उत्तर :
यहाँ X = स्थायी ग्राहकों के बिल की राशि बिलकी राशि का माध्य µ और प्रमाप विचलन δ है। ∴ z₁ = \(\frac{x-\mu}{8}\)

(i) 7.78% ग्राहकों का मासिक बिल ₹ 3590 से कम है।
∴ P(x ≤ 359) = \(\frac{7.78}{100}\) = 0.0778 ∴ P(Z ≤ z₁) = 0.0778
= 0.0778 = P(-α< Z ≤ 0)- P(z₁ ≤ Z ≤ 0)
∴ 0.0778= 0.5 – P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0) = 0.5 – 0.0778 = 0.4222 क्षेत्रफल के लिए प्रामाण्य चल का क्षेत्रफल तालिका को विलोम रूप से देखने पर z₁ = -1.42 प्राप्त होगा।
∴ z₁ = \(\frac{x_1-\mu}{\delta}\) -1.42 = \(\frac{3590-\mu}{\delta}\) -1.42δ = 3590 – µ ………….. (i)

(ii) 94.52% ग्राहकों का मासिक बिल की राशि ₹ 5100 से कम है।
∴ P(x ≤ 5100) = \(\frac{94.52}{100}\) = 0.9452 ∴ P(Z ≤ z₁) = 0.9452 जहाँ z₁ = \(\frac{x_1-\mu}{\delta}\)
0.9452 = P(-a < Z ≤ 0) + P(0 ≤ Z ≤ z₂)
∴ 0.9452 = 0.5 + P(0 ≤ Z ≤ z₂)
∴ 0.9452 – 0.5 = P(0 ≤ Z ≤ z₂)
∴ P(O ≤ Z ≤ z₁) = 0.4452 क्षेत्रफल के लिए प्रमाणित प्रामाण्य चल की सारणी विलोम रूप से देखने पर z₂ = 1.6 प्राप्त होता है।
∴ z₂ = \(\frac{x_2-\mu}{\delta}\) 1.6 = \(\frac{5100-\mu}{\delta}\) -1.6δ = 5100 – μ ……………….. (ii) परिणाम (i) और (ii) की तुलना करने पर

∴ δ = \(\frac{-1510}{-3.02}\) ∴ δ = 500
प्रमाप विचलन = 500 होगा समीकरण (ii) में δ = 500 रखने पर
1.6(500) = 5100 – µ 800 + µ = 5100
µ = 5100 – 800
µ = 4300
माध्य = 4300
प्रामाण्य वितरण के प्राचल माध्य = µ = 4300 प्रमाप विचलन = δ = 500 ∴ δ² = 250000

माना कि एकदम बीच के 95% ग्राहकों का मासिक बिल की राशि x₁ और x₂ के बीच होने की संभावना 0.95 होगा अर्थात् P(x₁ ≤ x ≤ x₂) = 0.95 होगा।
∴ P(\(\frac{x_1-\mu}{\delta} \leq \frac{x-\mu}{\delta} \leq \frac{x_2-\mu}{\delta}\)) = 0.95 ∴ P(z₁ ≤ Z ≤ z₂) = 0.95 जहाँ z₁ = \(\frac{x_1-4300}{500}\) और z₂ = \(\frac{x_2-4300}{500}\) है।

0.95 = P(z₁ ≤ z ≤ 0) + P(0 ≤ Z ≤ z₂)
अब x₁ और x₂ यह माध्य µ में से समान अंतर पर होने से z = 0 से z = z₁ और
z = z₂ के बीच का क्षेत्रफल (संभावना) दो समान हिस्सा करता है।
∴ P(z₁ ≤ Z ≤ 0) = 0.475 और P(0 ≤ Z ≤ z₂) = 0.475 होगा 0.475 के नजदीक का मूल्य 1.96 प्राप्त होगा।
∴ z = – 1.96 और z₂ = 1.96
∴ z₁ = \(\frac{x_1-\mu}{\delta}\) 1.96 = \(\frac{x_1-4300}{500}\) -1.96 × 500 = x₁ -4300 -980 + 4300 = x₁ ∴ x₁ = 3320
∴ z₂ = \(\frac{x_2-\mu}{\delta}\) 1.96 = \(\frac{x_2-4300}{500}\) 1.96 × 500 = x₂ -4300 980 + 4300 = x₂ ∴ x₂ = 5280
एकदम बीच में आते 95% ग्राहकों का मासिक बिल की राशि का अंतराल ₹ 3320 से ₹ 5280 होगा।

प्रश्न 7.
प्रामाण्य चल X का संभावना फलन निम्नानुसार है :
f(x) = \(\) = :-α < x < α
इस पर से निम्न मूल्यों को प्राप्त कीजिए:
(i) P(60 ≤ x ≤ x₂) = 0.5670 हो, तो x₂ ज्ञात कीजिए।
(ii) P(x₁ ≤ x ≤ 125) = 0.3979 हो, तो x₁ ज्ञात कीजिए
(iii) P|x – 50 ≤ 10| का मूल्य ज्ञात कीजिए।
उत्तर :
दिया गया संभावना फलन को प्रामाण्य चल X का संभावना घटत्व फलन के साथ तुलना करने पर

0.5670 = P(z₁ ≤ Z ≤ 0) + P(0 ≤ z ≤ z₂)
0.5670 = 0.1179 + P(0 ≤ Z ≤ z₂)
∴ 0.5670 – 0.1179 = P(0 ≤ Z ≤ z₂)
∴ P(0 ≤ Z ≤ z) = 0.4491 क्षेत्रफल के लिए प्रामाणित प्रामाण्य चल की सारणी को विलोम रूप से देखने पर 1.64
z₂ = \(\frac{x_2-75}{\delta}\) z₂ = 1.64
∴ 1.64 = \(\frac{x_2-75}{50}\) ∴ 1.64 × 50 = x₂ – 75
∴ 82 +75 = x₂ ∴ x₂ = 157

(ii) P(x ≤ x ≤ 125)= 0.3979 हो, तो x₁ ज्ञात कीजिए।
P(x₁ ≤ x ≤ 125) = P(\(\frac{x_1-75}{50} \leq \frac{x-\mu}{\delta} \leq \frac{125-75}{50}\)) = 0.3979 =P(z₁ ≤ Z ≤ 1)= 0.3979
0.3979 = P(z₁ ≤ Z ≤ 0) + P(0 ≤ Z ≤ z)
∴ 0.3979 = P(z₁ ≤ Z ≤ 0) + P(0 ≤ Z ≤ 1)
∴ 0.3979 = P(z₁ ≤ Z ≤ 0) + 0.3413
∴ 0.3979 – 0.3413 = P(z₁ ≤ Z ≤ 0)
0.0566 = P(z₁ ≤ Z ≤ 0)
∴ P(z₁ ≤ Z ≤ 0)= 0.0566 क्षेत्रफल के लिए प्रामाणित प्रामाण्य चल की सारणी को विलोम रूप से देखने पर z₁ = -0.14
∴ z₁ = \(\frac{x_1-\mu}{\delta}\) -0.14 = \(\frac{x_1-75}{50}\)
-0.14 × 50 = x₁ – 75 -75 + 7 = x₁
∴ x₁ = 68

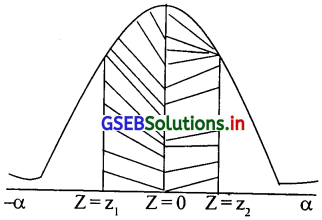
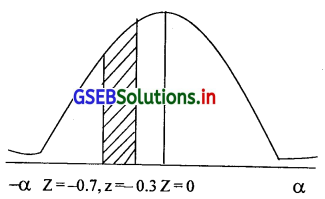
(iii) P(|x-50|≤ 10) का मूल्य ज्ञात कीजिए।
P(|x -50| ≤ 10) = P(-10 ≤ (x – 50) ≤ 10) (मानांक की परिभाषा)
= P(-10 + 50 ≤ (x – 50) + 50 ≤ 10 + 50) = P(40 ≤ x ≤ 60)
= P(\(\frac{40-75}{50} \leq \frac{x-\mu}{\delta} \leq \frac{60-75}{50}\))
= P(-0.7 ≤ Z ≤ -0.3)
= P(-0.7 ≤ Z ≤ 0) – P(-0.3 ≤ Z ≤ 0)
= 0.2580 – 0.1179
= 0.1401
P(|x-50| ≤ 10)= 0.1401 होगा।

प्रश्न 8.
एक प्रामाण्य चल X का संभावना फलन निम्नानुसार है:
f(x) अचलांक \(e^{-\frac{1}{200}(x-50)^2}\) :-α < x < α

इस वितरण पर से निम्न प्रश्नों के उत्तर दीजिए :
(1) मध्य का मूल्य ज्ञात कीजिए।
(2) अंतिम चतुर्थक की अनुमानित मूल्य ज्ञात कीजिए।
(3) चतुर्थक विचलन की अनुमानित मूल्य ज्ञात कीजिए।
(4) औसत विचलन की अनुमानित मूल्य ज्ञात कीजिए।
उत्तर :
दिया गया संभावना फलन के प्रामाण्य चल X का संभावना घटत्व फलन के साथ तुलना करने पर
उत्तरः

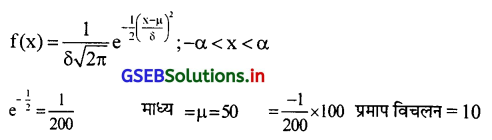
∴ δ² = 100 ∴ δ = 10

(i) मध्यक का मूल्य ज्ञात कीजिए।
प्रमाणित चल में माध्य = मध्यका होता है। ∴ µ = 50 है ∴ मध्यका = 50

(ii) अंतिम चतुर्थक की अनुमानित मूल्य ज्ञात कीजिए।
अंतिम चतुर्थक Q₁ और Q₃ है।
Q₁ (प्रथम चतुर्थक) का अनुमानित मूल्य
∴ Q₁ = µ – 0.675δ = 50 – 0.675(10) = 50 – 6.75
∴ Q₁ = 43.25
Q₃ = (तृतीय चतुर्थक) का अनुमानित मूल्य
Q₃ = µ + 0.6758
∴ Q₃ = 50 + 0.675(10) = 50 + 6.75
∴ Q₃ = 56.75

(iii) चतुर्थक विचलन का अनुमानित मूल्य ज्ञात कीजिए।
चतुर्थक विचलन = \(\frac {2}{3}\)δ = \(\frac {2}{3}\) × 10 = \(\frac {20}{3}\)
चतुर्थक विचलन का अनुमानित भूल्य = \(\frac {20}{3}\)

(iv) औसत विचलन का अनुमानित मूल्य ज्ञात कीजिए।
औसत विचलन = \(\frac {4}{5}\)δ = \(\frac {4}{5}\) × 10 = 8
औसत विचलन का अनुमानित मूल्य = 8