GSEB Solutions Class 12 Statistics Part 2 Chapter 4 Limit Ex 4

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 4 Limit Ex 4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 4 Limit Ex 4

Section A

Answer the following questions by selecting a correct option from the given options:

Question 1.
What is the modulus form of 0.3 neighbourhood of 3?
(a)|x – 0.3|<3
(b) |x- 31 < 0.3
(c) |x + 3|< 0.3 (d) |x – 3| > 0.3
Answer:
(b) |x- 31 < 0.3

Question 2.
What is the interval form of 0.02 neighbourhood of -2?
(a) (1.98, 2.02)
(b) (- 1.98, 2.02)
(c) (- 2.02, -1.98)
(d) (- 2.02, 1.98)
Answer:
(c) (- 2.02, – 1.98)

Question 3.
What is the interval form of |x – 5| < 0.25?
(a) (4.75, 5.25)
(b) (- 4.75, + 5.25)
(c) (- 5.25, – 4.75)
(d) (- 5.25, 4.75)
Answer:
(a) (4.75, 5.25)

Question 4.
What is the interval form of |2x + 1| < \(\frac{1}{5}\) ?
(a) \(\left(-\frac{6}{5},-\frac{4}{5}\right)\)
(b) \(\left(-\frac{6}{10},-\frac{4}{10}\right)\)
(c) \(\left(\frac{4}{10}, \frac{6}{10}\right)\)
(d) \(\left(-\frac{6}{10}, \frac{4}{10}\right)\)
Answer:
(b) \(\left(-\frac{6}{10},-\frac{4}{10}\right)\)

Question 5.
What is the modulus form of N (5, 0.02) ?
(a) |x + 5|< 0.02
(b) |x – 0.02| < 5 (c) |x – 5| > 0.02
(d) |x – 5| < 0.02
Answer:
(d) |x – 5| < 0.02

Question 6.
If modulus form of N (a, 0.07) is |x – 10| < k, then what will be the value of k?
(a) a
(b) 0.7
(c) 0.07
(d) 9.93
Answer:
(c) 0.07

Question 7.
What is the value of ?
(a) 9
(b) 10
(c) \(\frac{4}{3}\)
(d) 8
Answer:
(d) 8

Question 8.
What is the value of ?
(a) 5
(b) 25
(c) \(\frac{7}{4}\)
(d) 7
Answer:
(a) 5

Question 9.
What is the value of ?
(a) 10
(b) – 2
(c) 8
(d) Indeterminate
Answer:
(a) 10

Question 10.
What is the value of ?
(a) 192
(b) 324
(c) 36
(d) 108
Answer:
(d) 108

Question 11.
What is the value of ?
(a) – 5
(b) 5
(c) 4
(d) – 4
Answer:
(b) 5

Question 12.
If y = 10 – 3x and x → – 3, then y tends to which value ?
(a) 1
(b) 9
(c) 19
(d) 7
Answer:
(c) 19

Section B

Answer the following questions in one sentence:

Question 1.
Express 0.09 neighbourhood of 0 in interval form.
Answer:
0.09 neighbourhood of 0 in interval form is expressed by (0 – 0.09, 0 + 0.09) = (- 0.09, 0.09).

Question 2.
Express 0.001 neighbourhood of – 5 in modulus form.
Answer:
0.001 neighbourhood of – 5 in modulus form is expressed by
|x – (- 5) | < 0.001 = |x + 5] < 0.001.

Question 3.
Express |x – 10| < \(\frac{1}{10}\) in neighbourhood form.
Answer:
|x – 10| < \(\frac{1}{10}\) in neighbourhood form is expressed by N (10, \(\frac{1}{10}\)).

Question 4.
Express |2x| < \(\frac{1}{2}\) in interval form.
Answer:
|2x| < \(\frac{1}{2}\) in interval form is expressed by \(\left(-\frac{1}{4}, \frac{1}{4}\right)\)

Question 5.
Express N (50, 0.8) in modulus form.
Answer:
N (50, 0.8) in modulus form is expressed by |x – 50| < 0.8.

Question 6.
If N(a, 0.2) = |x – 7|< b, then find the value of a.
Answer:
N (a, 0.2) = | x – 7| < b
If N (a, 0.2) = |x – 7| < b, then a = 7.

Question 7.
If |x + 4| < 0.04 = (k, – 3.96), then find the value of fc.
Answer:
If |x + 4| < 0.04 = (k, – 3.96), then
a – δ = k; where a = – 4, δ = 0.04
∴ k = – 4 – 0.04 = – 4.04

Question 8.
Find the value of .
Answer:
= 3 (5) + 5 = 20

Question 9.
Find the value of .
Answer:

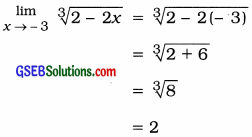
Question 10.
Find the value of ?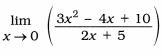
Answer:

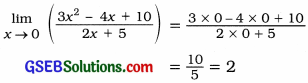
Question 11.
Find the value of
Answer:

Question 12.
Find the value of where m is an odd number.
Answer:

Question 13.
If  then find the value
Answer:

= 6 = 4 (- 1) + k = 6
∴ k = 6 + 4 = 10

Question 14.
If , then find the value of k.
Answer:

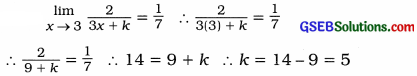
Section C

Answer the following questions as required:

Question 1.
Define an open interval.
Answer:
If a, b ∈ R and a < b, then the set of all real numbers between a and b not including a and b is called an open interval. It is denoted by (a, b).
Thus, (a, b) = {x|a < x < b, x ∈ R}.

Question 2.
Define the 5 neighbourhood of a.
Answer:
If a ∈ R and δ is non-negative real number, then the open interval (a – δ, a + δ) is called δ neighbourhood of a. It is denoted by N (a, δ). Thus,
N (a, δ) = {x|(a – δ) < x < (a + δ), x ∈ R}
= {x| |x – a| < δ. x ∈ R}

Question 3.
Define the punctured δ neighbourhood of a.
Answer:
If a ∈ R and δ is a non-negative real number, then the open interval (a – δ, a + δ) – {a} is called punctured δ neighbourhood of a. It is denoted by N* (a, δ). Thus,
N* (a, δ) = N(a, δ) – {a}
= {x | (a – δ) < x < (a + δ); x ≠ a, x ∈ R}
= {x | |x – a| < δ; x ≠ a, x ∈ R}

Question 4.
Express the interval form (- 0.5, 0.5) in modulus form.
Answer:
Interval form: {- 0.5, 0.5)
∴ a – δ = – 0.5, a + δ = 0.5
By adding, 2a = 0 ∴ a = 0
Putting a = 0 in a + δ, δ = 0.5
In modulus form: |x – a| < δ
∴ For (- 0.5, 0.5), modulus form is expressed by |x – 0| < 0.5 = |x| < 0.5

Question 5.
Express the interval form (- 8.75, – 7.25) in neighbourhood form.
Answer:
Interval form : (- 8.75, – 7.25)
∴ a – δ = – 8.75, a + δ = – 7.25
By adding, 2a = – 16 . ∴ a = – 8
Putting a = – 8 in a + δ = – 7.25,
– 8 + δ = – 7.25 ∴δ = – 7.25 + 8 = 0.75
δ neighbourhood of a: N (a, δ)
∴(- 8.75, – 7.25) in neighbourhood form
= N (- 8, 0.75)

Question 6.
If N (k₁, 0.5) = (19.5, k₂), then find the values of k₁ and k₂.
Answer:
N (k₁, 0.5) = (19.5, k₂)
k₁ – <5 = 19.5, k₁ + S = k₂
Here, δ = 0.5
∴ k₁ – 0.5 = 19.5
∴ k₁ = 19.5 + 0.5 = 20
Putting k₁ – 20 and δ = 0.5 in k₁ + δ = k₂,
20 + 0.5 = k₂
k₂ = 20.5
Hence, k₁ = 20, k₂ = 20.5

Question 7.
Express |3x + 1| < 2 in neighbourhood and interval form. ‘
Answer:
|3x + 1| < 2
∴ |x + \(\frac{1}{3}\)| < \(\frac{1}{3}\)
∴ \(\left|x-\left(-\frac{1}{3}\right)\right|<\frac{2}{3}\)
∴ \(\left|x-\left(-\frac{1}{3}\right)\right|<\frac{2}{3}\),
∴ a = – \(\frac{1}{3}\) δ = \(\frac{2}{3}\)

In neighbourhood form: N (a, δ)
∴ Neighbourhood form of |3x + 1| < 2
= N\(\left(-\frac{1}{3}, \frac{2}{3}\right)\)

In Interval form: (a – δ, a + δ)
Interval form of 13x + 11 < 2
= \(\left(-\frac{1}{3}-\frac{2}{3},-\frac{1}{3}+\frac{2}{3}\right)\)
= \(\left(-1, \frac{1}{3}\right)\)

Question 8.
If |x – A₁| < 0.09 = (A₂, 4.09), then find the values of A₁ and A₂.
Answer:
|x – A₁| < 0.09 = (A₂, 4.09)
∴ a – δ = A₂ and a + δ = 4.09
Here, δ = 0.09 and a = A₁
∴ A₁ – 0.09 = A₂ and A₁ + 0.09 = 4.09
Now, A₁ + 0.09 = 4.09
∴ A₁ = 4.09 – 0.09 = 4
Putting A₁ = 4 in A₁ – 0.09 = A₂,
4 – 0.09 = A₂
∴ A₂ = 3.91
Hence, A₁ = 4 and A₂ = 3.91

Question 9.
Explain the meaning of x → a.
Answer:
When the value of a variable x is brought very close to a number ‘a’ by increasing or decreasing its value, then it can be said that x tends to a. It is denoted by x → a.
x → a means that value of x is very close to a but x ≠ a.
Taking a = 1, let us understand the meaning of x → 1.

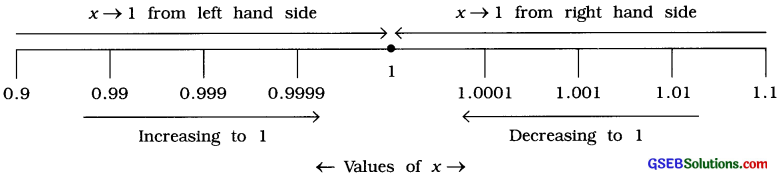
Question 10.
Explain the meaning of x → 0.
Answer:
If by decreasing the positive value of a variable x or by increasing the negative value of variable x, the value x is brought very close to ‘O’, then it can be said that x tends to ‘O’. It is denoted by x → 0.
x → 0 means that the value of x is very close to ‘0’ but x ≠ 0.
Let us understand the meaning of x → 0.

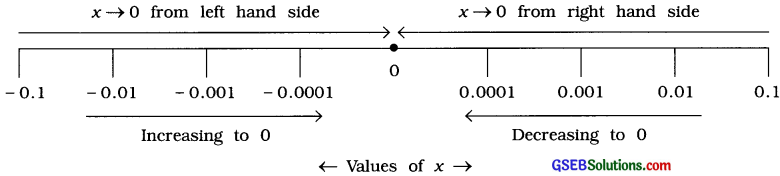
Question 11.
Define limit of a function.
Answer:
Limit of a function: When the value of a variable x Is brought closer and closer to a number ‘a’, the value of function f(x) approaches closer and closer to a definite number ‘l’, then we can say that as x tends to ‘a’ f(x) tends to ‘l’ that is x → a, f(x) → 1. This definite number ‘l’ is called limit of a function f(x). Symbolically it can be written as follows:

‘l’ is the limit of f(x). Hence f(x) ≠ l.

Question 12.
State multiplication working rule of limit.
Answer:
f(x) and g (x) are two functions of real variable x and f(x) = 1, g (x) = m.
If f (x) g ∙ (x) is the product of two functions, then multiplication working rule of limit is as follows:

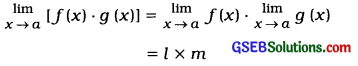
Thus, limit of product of two functions is equal to the product of limit of these two functions.

Question 13.
State division working rule of limit.
Answer:
f (x) and g (x) are two functions of real variable x and f(x) = 1, g (x) = m.
If \(\frac{f(x)}{g(x)}\) is the division of the two functions. then division working rule of limit is as follows:

Thus, the limit of division of two functions is equal to the division of their limits, where the limit of the function in denominator is not zero.

Question 14.
State the standard form of limit of a polynomial.
Answer:
Suppose, f(x) = a₀ + a₁x + a₂x² + …… + a_nxⁿ is a polynomial. The standard form of limit of a polynomial is as follows:

Section D

Find the values of the following:

Question 1.

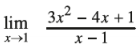
Answer:

Which is indeterminant. So x – 1 is common factor of the function. Eliminating this common factor from the numerator and denominator of the function limit of the function is found. We consider this matter, then and only then we will find the limit of the function.

Question 2.

Answer:

Question 3.

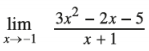
Answer:

Question 4.

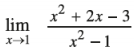
Answer:

Question 5.

Answer:

Question 6.

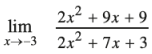
Answer:

Question 7.

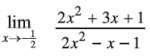
Answer:

Question 8.

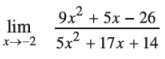
Answer:

Question 9.

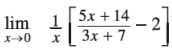
Answer:

Question 10.

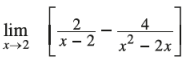
Answer:

Question 11.

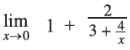
Answer:

Question 12.

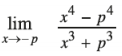
Answer:

Question 13.

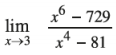
Answer:

Question 14.

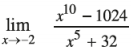
Answer:

Question 15.

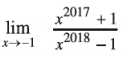
Answer:

Question 16.

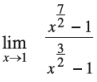
Answer:

Question 17.

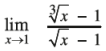
Answer:

Section E

I. Answer the following as required:

Question 1.
If y = 5x + 7 then using tabular method, prove that when x → 2, y → 17.
Answer:
y = 5x + 7
Here, x → 2. So taking the values of x very close to 2, the following table is prepared:

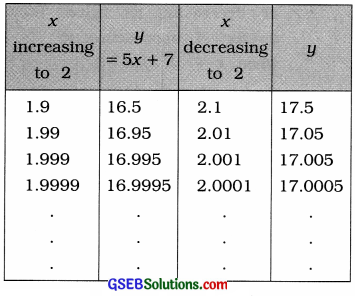
It is clear from the table that when x is brought nearer to 2 by increasing or decreasing its value the value of y = 5x + 7 approaches to 17. That is, when x → 2, y → 17.
Hence, it is proved that when x → 2, y → 17.

Question 2.
If y = \(\frac{3 x^{2}+16 x+16}{x+4}\) then using tabular method, prove that when x → – 4, y → – 8.
Answer:
y = \(\frac{3 x^{2}+16 x+16}{x+4}\)
= \(\frac{3 x^{2}+12 x+4 x+16}{x+4}\)
= \(\frac{3 x(x+4)+4(x+4)}{x+4}\)
= \(\frac{(x+4)(3 x+4)}{x+4}\)
= 3x + 4
Here, x → – 4. So taking the values of x very close to – 4, the following table is prepared:

It is clear from the table that when x is brought nearer to – 4 by increasing or decreasing its value, the value of y = 3x + 4 approaches to – 8. That is, when x → – 4, y → – 8.
Hence, it is proved that when x → – 4, y → – 8.

Question 3.
Using tabular method, prove that does not exist.
Answer:

Here, f(x) = \(\frac{3}{x+1}\)
x → – 1. So taking the values of x very close to – 1, the following table is prepared:

It is clear from the table that when x is brought nearer to – 1 by increasing or decreasing its value, the value of f(x) does not approach to a particular value. That is, when x → – 1, f(x) does not tend to a particular value.

Hence, it is proved that does not exist.

II. Find the values of the following using tabular method:

Question 1.

Answer:
Here, f(x) = \(\frac{x^{2}-3 x-10}{x-5}\)
Putting x = 5 in f(x)
f(x) = \(\frac{0}{0}\). So the common factor of numerator and denominator of f(x) is x – 5. After eliminating this common factor from f(x), we find the limit of f(x).
f(x) = \(\frac{x^{2}-5 x+2 x-10}{x-5}\)
= \(\frac{x(x-5)+2(x-5)}{x-5}\)
= \(\frac{(x-5)(x+2)}{x-5}\)
= x + 2

Taking the values of x very close to 5, the following table is prepared:

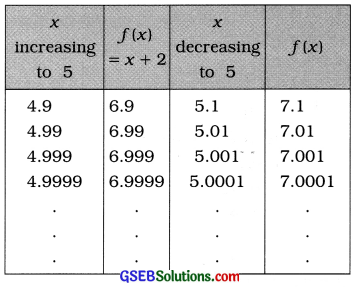
It is clear from the table that when x is brought nearer to 5 by increasing or decreasing its value. The value of f(x) approaches to 7. That is, when x → 5, f(x) → 7.

Question 2.

Answer:
f(x) = \(\frac{2 x^{2}+3 x-5}{x-1}\)
Putting x = 1 in f(x)
f(x) = \(\frac{0}{0}\). So the common factor (x – 1) of numerator and denominator of f(x), limit is found by tabular method.
f(x) = \(\frac{2 x^{2}+3 x-5}{x-1}\)
= \(\frac{2 x^{2}+5 x-2 x-5}{x-1}\)
= \(\frac{x(2 x+5)-1(2 x+5)}{x-1}\)
= \(\frac{(2 x+5)(x-1)}{x-1}\)
= 2x + 5

Taking the values of x very close to 1, the following table is prepared:

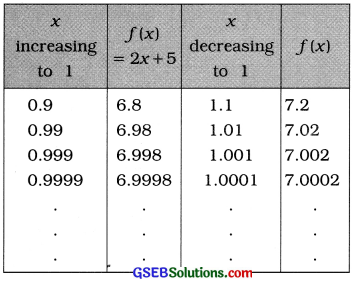
It is clear from the table that when x is brought nearer to 1 by increasing or decreasing its value, the value of f(x) approaches to 7. That is. when x → 1, f(x) → 7.

Question 3.

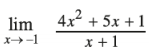
Answer:
Here, f(x) = \(\frac{4 x^{2}+5 x+1}{x+1}\)
Putting x = – 1 in f(x), we get f(x) = \(\frac{0}{0}\).
So after eliminating the common factor (x + 1) of numerator and denominator of f(x), the limit of f(x) is found.
f(x) = \(\frac{4 x^{2}+5 x+1}{x+1}\)
= \(\frac{4 x^{2}+4 x+x+1}{x+1}\)
= \(\frac{4 x(x+1)+1(x+1)}{x+1}\)
= \(\frac{(4 x+1)(x+1)}{(x+1)}\)
= 4x + 1

Taking the values of x very close to – 1, the following table is prepared:

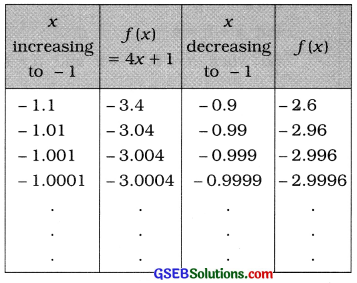
It is clear from the table that when x is brought nearer to – 1 by increasing or decreasing its value, the value of f(x) approaches to – 3. That is. when x → – 1, f(x) → – 3.

Question 4.

Answer:
Here, f(x) = 3x – 1 and x → 0. Taking the values of x very close to 0, the following table is prepared:

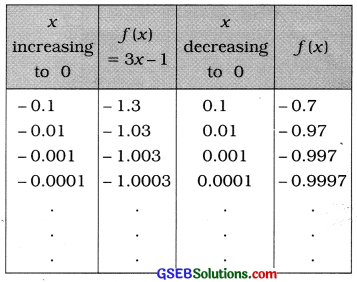
It is clear from the table that when x is brought nearer to 0 by increasing or decreasing its value, the value of f(x) approaches to – 1. That is. when x → 0, f(x) → – 1.

III. Find the values of the following:

Question 1.

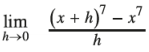
Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

Question 7.

Answer:

Question 8.

Answer:
f(x) = 2x² + 3
∴f(2 + h) = 2(2 + h)² + 3
= 2 (4 + 4h + h²) + 3
= 8 + 8h + 2h² + 3
= 2h² + 8h + 11
f(2) = 2 (2²) + 3 = 2 × 4 + 3 = 8 + 3 = 11

Question 9.

Answer:
f(x) = x²
∴ f(2 + x) = (2 + x)² = 4 + 4x + x²
f(2 – x) = (2 – x)² = 4 – 4x + x²

Question 10.

Answer:
f(x) = x² + x
∴ f(2) = (2)² + 2 = 4 + 2 = 6