Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 4 Limit Ex 4.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 4 Limit Ex 4.2
Question 1.
Find the values of the following using tabular method:
(1) ![]()
Answer:
Here, f(x) = 2x + 1. Taking the values of x very close to 1, the following table is prepared:
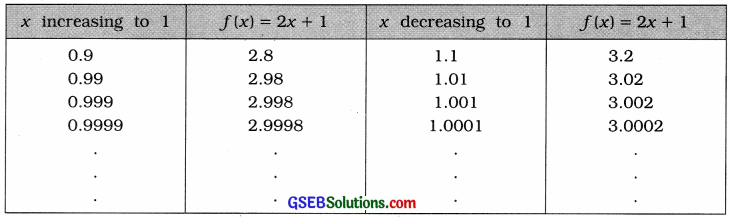
It is clear from the table that when x is brought nearer to 1 by increasing or decreasing its value, the value of f(x) approaches to 3. That is, when x → 1, f(x) → 3
![]()

(2) ![]()
Answer:
Here, f(x) = \(\frac{x^{2}-2 x-3}{x-3}\)
= \(\frac{x^{2}-3 x+x-3}{x-3}\)
= \(\frac{(x+1)(x-3)}{x-3}\)
= x + 1
Taking the values of x very close to 3, the following table is prepared:
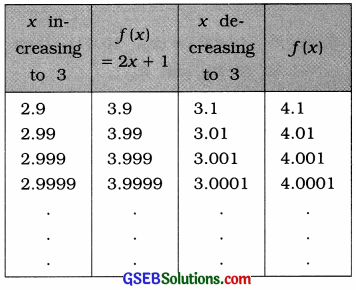
It is clear from the table that when x is brought nearer to 3 by increasing or decreasing its value, the value of f(x) approaches to 4. That is, when x → 3, f(x) → 4.
![]()

(3) ![]()
Answer:
Here, f(x) = \(\frac{2 x^{2}+3 x-14}{x-2}\)
= \(\frac{2 x^{2}+7 x-4 x-14}{x-2}\)
= \(\frac{(x-2)(2 x+7)}{x-2}\)
= 2x + 7
Taking the values of x very close to 2, the following table is prepared:

It is clear from the table that when x is brought nearer to 2 by increasing or decreasing its value, the value of f(x) approaches to 11. That is, when x → 2, f(x) → 11
![]()
(4) ![]()
Answer:
Here, f(x) = \(\frac{2 x^{2}+9 x+9}{x+3}\)
= \(\frac{2 x^{2}+6 x+3 x+9}{x+3}\)
= \(\frac{(2 x+3)(x+3)}{x+3}\)
= 2x + 3
Taking the values of x very close to – 3, the following table is prepared:
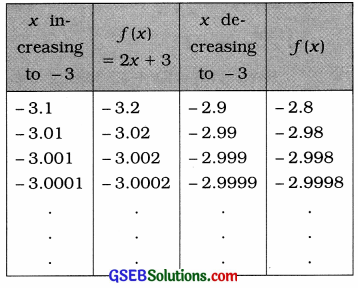
It is clear from the table that when x is brought nearer to – 3 by increasing or decreasing its value, the value of f(x) approaches to – 3. That is, when x → – 3, f(x) → – 3
![]()

(5) ![]()
Answer:
Here, f(x) = x. Taking the values of x very close to 2, the following table is prepared:

It is clear from the table that when x is brought nearer to 2 by increasing or decreasing its value, the value of f(x) approaches to 2. That is, when x → 2, f(x) → 2.
![]()
Question 2.
Using tabular method, show that ![]() does not exist.
does not exist.
Answer:
Here, f(x) = \(\frac{2}{x-3}\). Taking the values of x very close to 3. the following table is prepared:
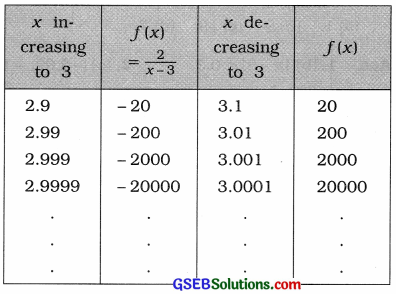
It is clear from the table that when x is brought nearer to 3 by increasing or decreasing its value, the value of f(x) does not approaches to a definite value. That is, when x → 3, f(x) does not tend to a definite value. Hence, the limit of this function does not exist.
![]() does not exist.
does not exist.

Question 3.
If y = \(\frac{x^{2}+x-6}{x-2}\), show that as x → 2, then y → 5 using tabular method.
Answer:
Here, y = \(\frac{x^{2}+x-6}{x-2}\)
= \(\frac{x^{2}+3 x-2 x-6}{x-2}\)
= \(\frac{(x-2)(x+3)}{x-2}\)
= x + 3
We have to prove that, when x → 2, then y → 5. So we have to find ![]()
Here, y = x + 3. Taking the values of x very close to 2, the following table is prepared :
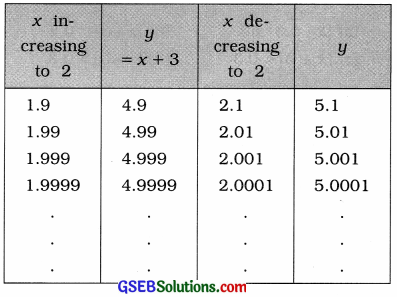
It is clear from the table that when x is brought nearer to 2 by increasing or decreasing its value, the value of y approaches to 5. That is, when x → 2, y → 5.
Hence, it is proved that when x → 2, then y → 5.

Question 4.
If y = 5 – 2x, show that as x → – 1 then y → 7 using tabular method.
Answer:
Here, y = 5 – 2x. Taking the values of x very close to – 1, the following table is prepared:
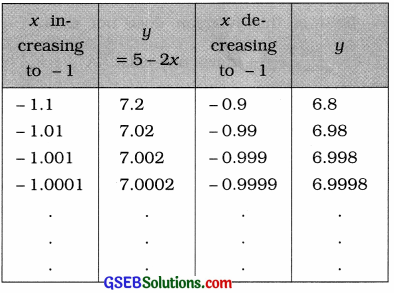
It is clear from the table that when x is brought nearer to – 1 by increasing or decreasing its value, the value of y approaches to 7. That is, when x → – 1, y → 7.
Hence, it is proved that when x → – 1, then y → 7.