Gujarat Board GSEB Solutions Class 6 Maths Chapter 12 ગુણોત્તર અને પ્રમાણ Ex 12.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 12 ગુણોત્તર અને પ્રમાણ Ex 12.1
પ્રશ્ન 1.
એક વર્ગમાં 20 છોકરીઓ અને 15 છોકરાઓ છે:
(a) છોકરીઓની સંખ્યા અને છોકરાઓની સંખ્યાનો ગુણોત્તર કેટલો છે?
(b) છોકરીઓ અને વર્ગના કુલ વિદ્યાર્થીઓનો ગુણોત્તર કેટલો હશે?
જવાબઃ
વર્ગમાં છોકરીઓની સંખ્યા = 20
વર્ગમાં છોકરાઓની સંખ્યા = 15
વર્ગમાં વિદ્યાર્થીઓની કુલ સંખ્યા = 20 + 15 = 35
(a) છોકરીઓની સંખ્યા અને છોકરાઓની સંખ્યાનો ગુણોત્તર
= \(\frac{20}{15}\) = \(\frac{20 \div 5}{15 \div 5}\)= \(\frac{4}{3}\) [∵ 20 અને 15નો ગુ.સા.અ. 5]
= 4 : 3
(b) છોકરીઓની સંખ્યા અને વર્ગના કુલ વિદ્યાર્થીઓનો ગુણોત્તર
= \(\frac{20}{35}\) = \(\frac{20 \div 5}{35 \div 5}\)= \(\frac{4}{7}\) [∵ 20 અને 35નો ગુ.સા.અ. 5].
= 4 : 7
પ્રશ્ન 2.
વર્ગના 30 વિદ્યાર્થીઓમાંથી 6ને ફૂટબૉલ, 12ને ક્રિકેટ અને બાકીનાને ટેનિસ ગમે છે, તો નીચેના ગુણોત્તર શોધોઃ
(a) ફૂટબૉલ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યા અને ટેનિસ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યા
(b) ક્રિકેટ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યા અને કુલ વિદ્યાર્થીઓની સંખ્યા
જવાબઃ
વર્ગમાં વિદ્યાર્થીઓની કુલ સંખ્યા = 30
તેમાંથી ફૂટબૉલ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યા = 6
તથા ક્રિકેટ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યા = 12
તથા ટેનિસ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યા = 30 – (6 + 12)
= 30 – 18 = 12
(a) ફૂટબૉલ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યાનો અને ટેનિસ ગમે છે
તેવા વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
= \(\frac{6}{12}\) = \(\frac{6 \div 6}{12 \div 6}\)= \(\frac{1}{2}\) [∵ 6 અને 12નો ગુ.સા.અ. 6].
= 1 :2
(b) ક્રિકેટ ગમે છે તેવા વિદ્યાર્થીઓની સંખ્યાનો અને વર્ગના કુલ
વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
= \(\frac{12}{30}\) = \(\frac{12 \div 6}{30 \div 6}\)= \(\frac{2}{5}\) [∵ 12 અને 30નો ગુ.સા.અ. 6)
= 2 : 5
પ્રશ્ન 3.
નીચેની આકૃતિ પરથી ગુણોત્તર શોધોઃ
(a) લંબચોરસની અંદર આવેલા ત્રિકોણની સંખ્યા અને વર્તુળની સંખ્યાનો
(b) લંબચોરસની અંદર આવેલા ચોરસની સંખ્યા અને કુલ આકારોની સંખ્યાનો
(c) લંબચોરસની અંદર આવેલા વર્તુળની સંખ્યા અને કુલ આકારોની સંખ્યાનો
જવાબઃ
અહીં, આપેલા ત્રિકોણની કુલ સંખ્યા = 3
અહીં, આપેલા ચોરસની કુલ સંખ્યા = 2
અહીં, આપેલા વર્તુળની કુલ સંખ્યા = 2
અહીં, આપેલાં કુલ આકારોની સંખ્યા = 3 + 2 + 2 = 7
(a) ત્રિકોણની સંખ્યા અને વર્તુળની સંખ્યાનો ગુણોત્તર = \(\frac{3}{2}\) = 3 : 2
(b) ચોરસની સંખ્યા અને કુલ આકારની સંખ્યાનો ગુણોત્તર = \(\frac{2}{7}\) = 2 : 7
(c) વર્તુળની સંખ્યા અને કુલ આકારની સંખ્યાનો ગુણોત્તર = \(\frac{2}{7}\) = 2 : 7
પ્રશ્ન 4.
હમીદ અને અખ્તર અનુક્રમે 1 કલાકમાં 9 કિમી અને 12 કિમી અંતર કાપે છે. હમીદની ઝડપ અને અખ્તરની ઝડપનો ગુણોત્તર શોધો.
જવાબ:
હમીદની ઝડપ = 9 કિમી કલાક
અખ્તરની ઝડપ = 12 કિમી / કલાક
હમીદની ઝડપ અને અખ્તરની ઝડપનો ગુણોત્તર =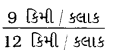 
= \(\frac{9 \div 3}{12 \div 3}\) = \(\frac{3}{4}\) [∵ 9 અને 12નો ગુ.સા.અ. 3]
= 3 : 4
પ્રશ્ન 5.
નીચેનાં ખાનાં પૂર્ણ કરો:
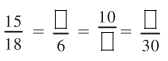(શું આ ગુણોત્તરો સરખા છે?)
જવાબ:
દરેકમાં ચોકડી ગુણાકાર કરતાં,
આમ,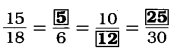 
હવે, આપણે ચકાસીએ કે આ બધા ગુણોત્તરો સરખા ગુણોત્તર છે કે કેમ, દરેક ગુણોત્તરનું અતિસંક્ષિપ્ત સ્વરૂપ આપીએ.
= \(\frac{15}{18}\) =\(\frac{15 \div 3}{18 \div 3}\) = \(\frac{5}{6}\) [∵ 15 અને 18નો ગુ.સા.અ. 3]
= \(\frac{10}{12}\) =\(\frac{10 \div 2}{12 \div 2}\) = \(\frac{5}{6}\) [∵ 10 અને 12નો ગુ.સા.અ. 2]
= \(\frac{25}{30}\) =\(\frac{25 \div 5}{30 \div 5}\) = \(\frac{5}{6}\) [∵ 25 અને 30નો ગુ.સા.અ. 5].
આમ, બધા ગુણોત્તરોનું અતિસંક્ષિપ્ત સ્વરૂપ છે છે, તેથી બધા ગુણોત્તરો સરખા છે.
પ્રશ્ન 6.
નીચેનાનો ગુણોત્તર શોધોઃ
(a) 81 અને 108
જવાબ :
ગુણોત્તર = \(\frac{81}{108}\)
= \(\frac{81 \div 27}{108 \div 27}\) = \(\frac{3}{4}\) [∵ 81 અને 108નો ગુ.સા.અ. 27]
= 3 : 4
(b) 98 અને 63
જવાબ:
ગુણોત્તર = \(\frac{98}{63}\)
= \(\frac{98 \div 7}{63 \div 7}\) = \(\frac{14}{9}\) [∵ 98 અને 63નો ગુ.સા.અ. 7]
= 14 : 9
(c) 33 કિમી અને 121 કિમી
જવાબ:
ગુણોત્તર =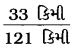 
= \(\frac{33 \div 11}{121 \div 11}\) = \(\frac{3}{11}\) [∵ 33 અને 121નો ગુ.સા.અ. 11]
= 3 : 11
(d) 30 મિનિટ અને 45 મિનિટ
જવાબ:
ગુણોત્તર =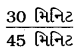 
= \(\frac{30 \div 15}{45 \div 15}\) = \(\frac{2}{3}\) [∵ 30 અને 45નો ગુ.સા.અ. 15].
= 2 : 3
પ્રશ્ન 7.
નીચેનાનો ગુણોત્તર શોધોઃ
(a) 30 મિનિટ અને 1.5 કલાક
જવાબ:
30 મિનિટ અને 1.5 કલાક
અહીં, 1.5 કલાકને મિનિટમાં ફેરવીશું. 1 કલાક = 60 મિનિટ છે.
∴ 1.5 કલાક = 15 × 60 મિનિટ = 90 મિનિટ
(b) 40 સેમી અને 1.5 મીટર
જવાબ:
40 સેમી અને 1.5 મીટર
અહીં, 1.5 મીટરને સેમીમાં ફેરવીશું. 1 મીટર = 100 સેમી છે.
∴ 1.5 મીટર = 6 × 100 સેમી = 150 સેમી
માગેલો ગુણોત્તર =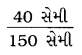 
= \(\frac{40 \div 10}{150 \div 10}\) [∵ 40 અને 150નો ગુ.સા.અ. 10].
= \(\frac{4}{15}\) = 4: 15
(c) 55 પૈસા અને 1 રૂપિયો
જવાબ:
55 પૈસા અને 1 રૂપિયા
અહીં, 1 રૂપિયાને પૈસામાં ફેરવીશું. 1 રૂપિયો = 100 પૈસા
માગેલો ગુણોત્તર =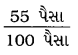 
= \(\frac{55 \div 5}{100 \div 5}\) [∵ 55 અને 100નો ગુ.સા.અ. 5].
= \(\frac{11}{20}\) = 11 : 20
(d) 500 મિલિ અને 2 લિટર
જવાબ:
500 મિલિ અને 2 લિટર
અહીં, 2 લિટરને મિલિમાં ફેરવીશું. 1 લિટર = 1000 મિલિ છે.
∴ 2 લિટર = 2 × 1000 મિલિ = 2000 મિલિ
માગેલો ગુણોત્તર =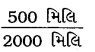 
= \(\frac{500 \div 500}{2000 \div 500}\) [∵ 500 અને 2000નો ગુ.સા.અ. 500]
= \(\frac{1}{4}\) = 1 : 4
પ્રશ્ન 8.
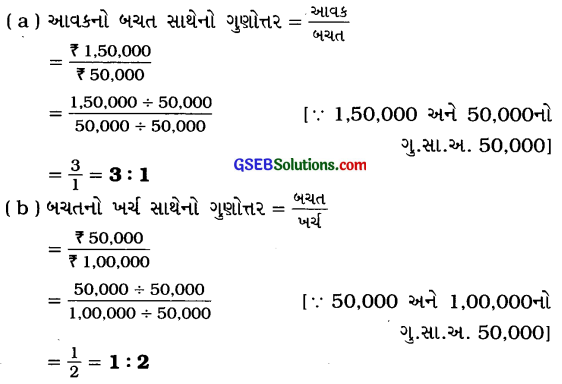
એક વર્ષમાં સીમા 1,50,000 કમાય છે અને 50,000 બચત કરે છે, તો નીચેના ગુણોત્તર શોધોઃ
(a) સીમા કમાય છે તે રકમ અને તે બચત કરે છે તે રકમનો
(b) તેણે બચાવેલ રકમ અને તેણે ખર્ચ કરેલ રકમનો
જવાબઃ
સીમાની કુલ આવક = ₹1,50,000
સીમાની કુલ બચત = ₹ 50,000
∴ સીમાનો કુલ ખર્ચ = ₹ 1,50,000 – ₹ 50,000
= ₹ 1,00,000
પ્રશ્ન 9.
3300 વિદ્યાર્થીઓની એક શાળામાં 102 શિક્ષકો છે. શિક્ષકોની સંખ્યા અને વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર શોધો.
જવાબ:
શાળામાં શિક્ષકોની કુલ સંખ્યા = 102
શાળામાં વિદ્યાર્થીઓની કુલ સંખ્યા = 3300
શિક્ષકોની સંખ્યાનો વિદ્યાર્થીઓની સંખ્યા સાથેનો ગુણોત્તર = \(\frac{102}{3300}\)
= \(\frac{102 \div 6}{3300 \div 6}\) [∵ 102 અને 3300નો ગુ.સા.અ. 6].
= \(\frac{17}{550}\) = 17 : 550
શિક્ષકોની સંખ્યા અને વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર 17:550 છે.
પ્રશ્ન 10.
એક કૉલેજના 4320 વિદ્યાર્થીઓમાંથી 2300 છોકરીઓ છે, તો નીચેના ગુણોત્તર શોધોઃ
(a) છોકરીઓની સંખ્યા અને કુલ વિદ્યાર્થીઓની સંખ્યાનો
(b) છોકરાઓની સંખ્યા અને છોકરીઓની સંખ્યાનો
(c) છોકરાઓની સંખ્યા અને કુલ વિદ્યાર્થીઓની સંખ્યાનો
જવાબઃ
કૉલેજમાં કુલ વિદ્યાર્થીઓની સંખ્યા = 4320
તેમાંથી છોકરીઓની સંખ્યા = 2300
∴ છોકરાઓની સંખ્યા = 4320 – 2300 = 2020
(a) છોકરીઓની સંખ્યા અને કુલ વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
(b) છોકરાઓની સંખ્યા અને છોકરીઓની સંખ્યાનો ગુણોત્તર
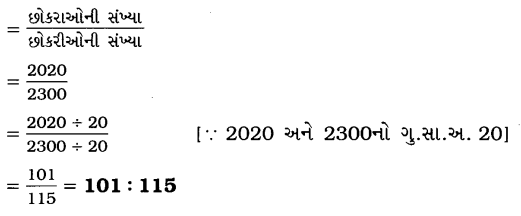
(c) છોકરાઓની સંખ્યા અને કુલ વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
પ્રશ્ન 11.
શાળાના 1800 વિદ્યાર્થીઓમાંથી 750એ બાસ્કેટ બૉલ, 800એ ક્રિકેટ અને બાકીનાએ ટેબલ ટેનિસની રમત પસંદ કરી. જો દરેક વિદ્યાર્થીએ માત્ર એક જ રમત પસંદ કરી હોય, તો નીચેના ગુણોત્તર શોધોઃ
(a) બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓ અને ટેબલ ટેનિસ પસંદ કરનાર વિદ્યાર્થીઓ
(b) ક્રિકેટ પસંદ કરનાર વિદ્યાર્થીઓ અને બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓ
(c) બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓ અને કુલ વિદ્યાર્થીઓની સંખ્યા
જવાબઃ
શાળાના કુલ વિદ્યાર્થીઓની સંખ્યા = 1800
બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યા = 750
ક્રિકેટ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યા = 800
∴ ટેબલ ટેનિસ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યા
= 1800 – [750 + 800]
= 1800 – 1550 = 250
(a) બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યા અને ટેબલ ટેનિસ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
= \(\frac{750}{250}\)
= \(\frac{750 \div 250}{250 \div 250}\) [∵ 750 અને 250નો ગુ.સા.અ. 250]
= \(\frac{3}{1}\) = 3 : 1
(b) ક્રિકેટ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યા અને બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
= \(\frac{800}{750}\)
= \(\frac{800 \div 50}{750 \div 50}\) [∵ 800 અને 750નો ગુ.સા.અ. 50].
= \(\frac{16}{15}\) = 16: 15
(c) બાસ્કેટ બૉલ પસંદ કરનાર વિદ્યાર્થીઓની સંખ્યાનો અને કુલ વિદ્યાર્થીઓની સંખ્યાનો ગુણોત્તર
= \(\frac{750}{1800}\)
= \(\frac{750 \div 150}{1800 \div 150}\) [∵ 750 અને 1800નો ગુ.સા.અ. 150]
= \(\frac{5}{12}\) = 5 : 12
પ્રશ્ન 12.
એક ડઝન પેનની કિંમત 180 રૂપિયા અને 8 બૉલપેનની કિંમત 50 રૂપિયા છે. પેન અને બૉલપેનની કિંમતનો ગુણોત્તર શોધો.
જવાબ:
1 ડઝન પેનની કિંમત 180 રૂપિયા છે.
એટલે કે 12 પેનની કિંમત 180 રૂપિયા છે.
∴ 1 પેનની કિંમત =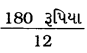 
= 15 રૂપિયા
8 બૉલપેનની કિંમત = 56 રૂપિયા
∴ 1 બૉલપેનની કિંમત =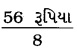 
= 7 રૂપિયા
પેનની કિંમત અને બૉલપેનની કિંમતનો ગુણોત્તર =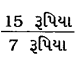 
= \(\frac{15}{7}\) = 15 : 7
પેનની કિંમત અને બૉલપેનની કિંમતનો ગુણોત્તર 15 : 7 છે.
પ્રશ્ન 13.
આપેલું વિધાન વિચારોઃ એક સભાખંડની પહોળાઈ અને લંબાઈનો ગુણોત્તર 2 : 5 છે. હૉલની આપેલ પહોળાઈ અને લંબાઈના આધારે નીચેનું કોષ્ટક પૂર્ણ કિરો:
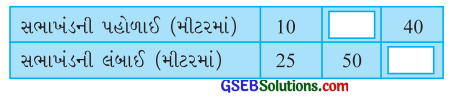
જવાબ:
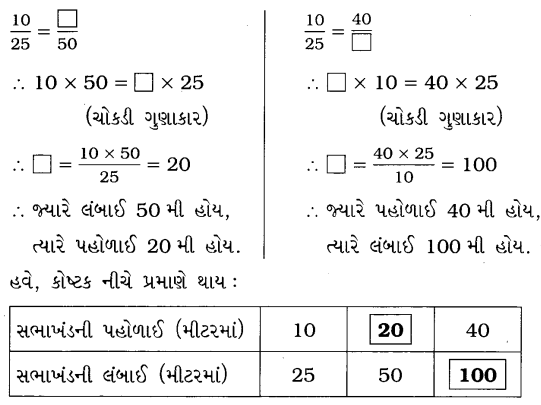
પ્રશ્ન 14.
શીલા અને સંગીતા વચ્ચે 20 પેન 3 : 2ના ગુણોત્તરમાં વહેચો.
જવાબ:
પેનની કુલ સંખ્યા = 20
શીલા અને સંગીતા વચ્ચે કુલ 20 પેન 3:2ના ગુણોત્તરમાં વહેંચવાની છે.
ગુણોત્તરનાં બંને પદોનો સરવાળો = 3 + 2 = 5
આમ, શીલાને કુલ પેનનો ભાગ મળે અને સંગીતાને કુલ પેનનો \(\frac{2}{5}\) ભાગ .
મળે.
∴ શીલાને મળતી પેન = 20 × \(\frac{3}{5}\) = 12
અને સંગીતાને મળતી પેન = 20 × \(\frac{2}{5}\) = 8
શીલાને 12 પેન અને સંગીતાને 8 પેન મળે.
પ્રશ્ન 15.
એક માતા પોતાની બે દીકરીઓ શ્રેયા અને ભૂમિકા વચ્ચે ર36 તેમની ઉંમરના ગુણોત્તરને આધારે વહેંચવા માગે છે. જો શ્રેયાની ઉંમર 15 વર્ષ અને ભૂમિકાની ઉંમર 12 વર્ષ છે, તો ભૂમિકા અને શ્રેયાને કેટલા રૂપિયા મળશે?
જવાબ:
માતા તેમની બંને પુત્રીઓ વચ્ચે 36 તેમની ઉંમરના ગુણોત્તરમાં વહેંચવા ઇચ્છે છે.
શ્રેયાની ઉંમર = 15 વર્ષ
ભૂમિકાની ઉંમર = 12 વર્ષ .
∴ શ્રેયાની ઉંમર અને ભૂમિકાની ઉંમરનો ગુણોત્તર
= 
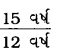
= \(=\frac{15 \div 3}{12 \div 3}\) [∵ 15 અને 12નો ગુ.સા.અ. 3]
= \(\frac{5}{4}\) = 5 : 4
આ ગુણોત્તરનાં બંને પદોનો સરવાળો = 5 + 4 = 9
કુલ ₹ 36 બંને વચ્ચે વહેંચવાના છે.
∴ શ્રેયાને મળતી રકમ = ₹ 36 × \(\frac{5}{9}\) = ₹ 20 અને
ભૂમિકાને મળતી રકમ = ₹ 36 × \(\frac{4}{9}\) = ₹ 16
શ્રેયાને ₹ 20 અને ભૂમિકાને ₹ 16 મળે.
પ્રશ્ન 16.
પિતાની હાલની ઉંમર 42 વર્ષ છે અને તેના પુત્રની ઉંમર 14 વર્ષ છે. નીચેના ગુણોત્તર શોધોઃ
(a) પિતાની હાલની ઉંમર અને પુત્રની હાલની ઉંમર
(b) જો પુત્ર 12 વર્ષનો હોય, તો પિતાની ઉંમર અને પુત્રની ઉંમર
(c) 10 વર્ષ પછી પિતા અને પુત્રની ઉંમરનો
(d) પિતા 30 વર્ષના હતા, ત્યારે પિતા અને પુત્રની ઉંમરનો
જવાબ :
(a) પિતાની હાલની ઉંમર = 42 વર્ષ
પુત્રની હાલની ઉંમર = 14 વર્ષ
∴ પિતાની હાલની ઉંમર અને પુત્રની હાલની ઉંમરનો ગુણોત્તર
= 
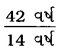
= \(\frac{42 \div 14}{14 \div 14}\) [∵ 42 અને 14નો ગુ.સા.અ. 14].
= \(\frac{3}{1}\) = 3 : 1
(b) જ્યારે પુત્રની ઉંમર 12 વર્ષ હતી એટલે કે
(14 વર્ષ – 12 વર્ષ) = 2 વર્ષ પહેલાં
પિતાની ઉંમર 42 વર્ષ -2 વર્ષ = 40 વર્ષ હશે.
પિતાની ઉંમર અને પુત્રની ઉંમરનો ગુણોત્તર
= 
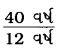
= \(\frac{40 \div 4}{12 \div 4}\) [∵ 40 અને 12નો ગુ.સા.અ. 4.]
= \(\frac{10}{3}\) = 10 : 3
(c) 10 વર્ષ પછી
પિતાની ઉંમર = 42 વર્ષ + 10 વર્ષ = 52 વર્ષ થશે.
પુત્રની ઉંમર = 14 વર્ષ + 10 વર્ષ = 24 વર્ષ થશે.
પિતાની ઉંમર અને પુત્રની ઉંમરનો ગુણોત્તર
= 
= \(\frac{52 \div 4}{24 \div 4}\) [∵ 52 અને 24નો ગુ.સા.અ. 4].
= \(\frac{13}{6}\) = 13 : 6
(d) જ્યારે પિતાની ઉંમર 30 વર્ષ એટલે કે
(42 વર્ષ-30 વર્ષ) = 12 વર્ષ પહેલાં
પુત્રની ઉંમર 14 વર્ષ – 12 વર્ષ = 2 વર્ષ હોય.
પિતાની ઉંમર અને પુત્રની ઉંમરનો ગુણોત્તર
= 
= \(\frac{30 \div 2}{2 \div 2}\) [∵ 30 અને 2નો ગુ.સા.અ. 2].
= \(\frac{15}{1}\) = 15 : 1