Gujarat Board GSEB Solutions Class 6 Maths Chapter 5 પાયાના આકારોની સમજૂતી Ex 5.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 5 પાયાના આકારોની સમજૂતી Ex 5.1
પ્રશ્ન 1.
માત્ર નિરીક્ષણ કરી રેખાખંડોની સરખામણી કરવામાં કયો ગેરલાભ થાય છે?
જવાબ:
માત્ર નિરીક્ષણ કરીને બે રેખાખંડોની લંબાઈનું અનુમાન કરવું કેટલીક વાર ખોટું પણ પડે. બાજુમાં આપેલી આકૃતિમાં \(\overline{\mathrm{AB}}\) અને \(\overline{\mathrm{CD}}\) રેખાખંડોમાં બંને રેખાખંડની લંબાઈ સરખી લાગે છે, પરંતુ ખરેખર બે રેખાખંડોની લંબાઈ સરખી નથી.
CD = 2 સેમી છે. જ્યારે AB = 2.5 સેમી છે.
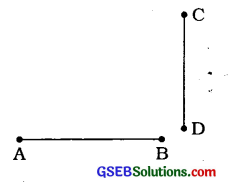
પ્રશ્ન 2.
રેખાખંડની લંબાઈ માપવા માટે માપપટ્ટી કરતાં દ્વિભાજક શા માટે વધુ ઉપયોગી છે?
જવાબ:
માપપટ્ટી વડે રેખાખંડની લંબાઈ માપતાં કેટલીક વાર પૂરેપૂરું સાચું માપ મેળવી શકાતું નથી. માપપટ્ટી પરના આંકાની પ્રમાણભૂતતા, માપપટ્ટીની જાડાઈ, આપણા માપનની રીતની ક્ષતિ કારણભૂત બને છે. આમ, રેખાખંડનું સાચું માપન કરવા દ્વિભાજકનો ઉપયોગ કરવો જોઈએ. દ્વિભાજક વડે રેખાખંડનું ચોક્કસ માપ મળે. દ્વિભાજકના પાંખિયાંમાં અણી હોય છે જેને લીધે માપપટ્ટી ઉપર મૂકવામાં અને રેખાખંડના અંત્યબિંદુએ મૂકવામાં ચોકસાઈ જળવાય છે.
![]()
પ્રશ્ન ૩.
કોઈ રેખાખંડ દોરી તેને \(\overline{\mathbf{A B}}\) કહો. કોઈ બિંદુ cને A અને B વચ્ચે રેખાખંડ પર દર્શાવો. \(\overline{\mathbf{A B}}\), \(\overline{\mathbf{B C}}\) અને \(\overline{\mathbf{A C}}\)ની લંબાઈ માપો. શું AB = AC + CB છે?
(નોંધઃ A, B અને C રેખા પરનાં એવાં બિંદુઓ હોય કે જેથી AC + CB થાય, તો ચોક્કસ કહી શકાય કે તે બિંદુ A અને Bની વચ્ચે હશે.)
જવાબ:
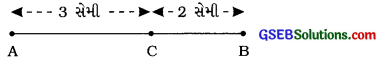
અહીં, આપણે 5 સેમી લંબાઈનો રેખાખંડ AB દોર્યો છે. \(\overline{\mathbf{A B}}\) ઉપર એક બિંદુ C લીધું છે.
હવે, \(\overline{\mathbf{A B}}\), \(\overline{\mathbf{A C}}\) અને \(\overline{\mathbf{C B}}\)નાં માપ માપીએ.
AB = 5 સેમી, AC = 3 સેમી અને CB = 2 સેમી છે. હવે,
AC + CB = 3 + 2 = 5 સેમી, વળી, AB = 5 સેમી
∴ AB = AC + CB
આથી કહી શકીએ કે બિંદુ C એ \(\overline{\mathbf{A B}}\) ઉપર આવેલું બિંદુ છે. જેથી AB = AC + CB થાય છે.
પ્રશ્ન 4.
રેખા પર ત્રણ બિંદુઓ AB અને C છે. જો AB = 5 સેમી, BC = 3 સેમી અને AC = 8 સેમી હોય, તો કયું બિંદુ બાકીનાં બેની વચ્ચે હશે?
જવાબ:
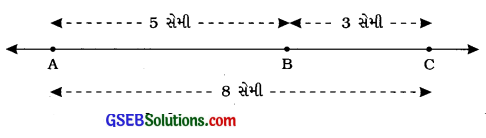
પ્રશ્નમાં આપ્યા પ્રમાણે એક રેખા પર 8 સેમી લંબાઈનો રેખાખંડ AC લઈએ. વળી, AC રેખાખંડ ઉપર AB = 5 સેમી થાય તેવું બિંદુ B લઈએ. હવે, BC = AC – AB = 8 – 5 = 3 સેમી થાય.
આ રીતે AB + BC = 5 + 3 = 8 સેમી, તેથી AB + BC = AC AC રેખાખંડ ઉપર બિંદુ B આવેલું છે, તેથી બિંદુ B એ બિંદુ A અને બિંદુ
Cની વચ્ચે આવેલું બિંદુ છે.
પ્રશ્ન 5.
ચકાસો કે D બિંદુ એ \(\overline{\mathbf{A G}}\)નું મધ્યબિંદુ છે.
જવાબ:

અહીં, સૌપ્રથમ આપણે A બિંદુથી D બિંદુ સુધીનું અંતર એટલે કે અંતર AD તથા D બિંદુથી 6 બિંદુ સુધીનું અંતર DG શોધીએ.
AD = AB + BC + CD = 1 + 1 + 1 = 3 એકમ
DG = DE + EF + FG = 1 + 1 + 1 = 3 એકમ
હવે, AG = AD + DG = 3 + 3 = 6 એકમ
આમ, AD = DG = 3 એકમ
D એ \(\overline{\mathrm{AG}}\) રેખાખંડ ઉપર આવેલું એવું બિંદુ છે કે જેથી A – D – G તથા AD = DG છે.
∴ D એ \(\overline{\mathrm{AG}}\)નું મધ્યબિંદુ છે.
પ્રશ્ન 6.
B એ \(\overline{\mathrm{AC}}\)નું મધ્યબિંદુ છે અને c એ \(\overline{\mathrm{BD}}\)નું મધ્યબિંદુ છે. A, B, C અને D એક જ રેખા પર છે. AB = CD શા માટે કહી શકાય?
જવાબ:
![]()
અહીં, બિંદુઓ A, B, C અને D એ એક જ રેખા ઉપર આવેલાં બિંદુઓ છે. પ્રશ્નમાં આપ્યા પ્રમાણે B એ \(\overline{\mathrm{AC}}\)નું મધ્યબિંદુ છે.
∴ AB = BC … … … (1)
વળી, C એ \(\overline{\mathrm{BD}}\)નું મધ્યબિંદુ છે.
∴ BC = CD .. … … (2)
અહીં, પરિણામ (1) અને (2) પરથી,
∴ AB = CD (∵ A – B – C – D)
![]()
પ્રશ્ન 7.
પાંચ ત્રિકોણ દોરી તેમની બાજુઓ માપો. દરેક સ્થિતિમાં ચકાસો કે કોઈ પણ બે બાજુનાં માપનો સરવાળો હંમેશાં તેની ત્રીજી બાજુ કરતાં વધુ જ હોય.
જવાબ:
(1) અહીં, ∆ ABC દોર્યો છે, જેમાં AB = 3 સેમી, A
BC = 2 સેમી અને AC = 4 સેમી છે.
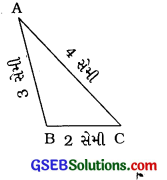
હવે, બે બાજુઓના માપના સરવાળાને ત્રીજી બાજુના માપ સાથે સરખાવીએ.
AB + BC = 3 સેમી + 2 સેમી = 5 સેમી, જે ત્રીજી બાજુ AC = 4 સેમી કરતાં વધારે છે.
એટલે કે AB + BC > AC
BC + AC = 2 સેમી + 4 સેમી = 6 સેમી, જે ત્રીજી બાજુ AB = 3 સેમી કરતાં વધારે છે.
એટલે કે BC + AC > AB
AB + AC = 3 સેમી + 4 સેમી = 7 સેમી, જે ત્રીજી બાજુ BC = 2 સેમી કરતાં વધારે છે.
એટલે કે AB + AC > BC
(2) અહીં, ∆ PQR દોર્યો છે, જેમાં PQ = 4.5 સેમી, QR = 5.5 સેમી અને PR = 8 સેમી છે.
હવે, બે બાજુઓના માપના સરવાળાને ત્રીજી બાજુના માપ સાથે સરખાવીએ.
PQ + QR = 4.5 સેમી + 5.5
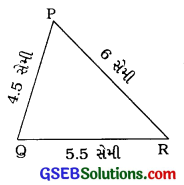
સેમી = 10 સેમી, જે ત્રીજી બાજુ PR = 6 સેમી કરતાં વધારે છે.
એટલે કે PQ + QR > PR
QR + PR = 5.5 સેમી + 6 સેમી = 11.5 સેમી, જે ત્રીજી બાજુ
PQ = 4.5 સેમી કરતાં વધારે છે.
એટલે કે QR + PR > PQ
PR + PQ = 6 સેમી + 4.5 સેમી = 10.5 સેમી, જે ત્રીજી બાજુ QR = 5.5 સેમી કરતાં વધારે છે.
એટલે કે PR + PG > QR
બાકીના ત્રણ ત્રિકોણો જાતે દોરો. આમ, આપણે કહી શકીએ કે ત્રિકોણની કોઈ પણ બે બાજુનાં માપનો સરવાળો હંમેશાં તેની ત્રીજી બાજુ કરતાં વધુ જ હોય.