Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 7 Fractions Ex 7.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 7 Fractions Ex 7.3
Question 1.
Write the fractions. Are all these fractions equivalent?
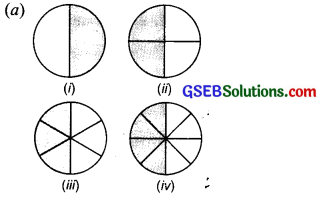
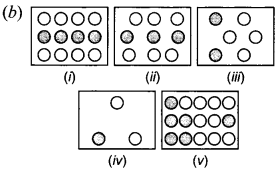
Solution:
(a) Fraction represented by,
Shaded part of (i) = \(\frac { 1 }{ 2 } \)
Shaded part of (ii) = \(\frac { 2 }{ 4 } \) = \(\frac{2 \div 2}{4 \div 2}\) = \(\frac { 1 }{ 2 } \)
Shaded part of (iii) = \(\frac { 3 }{ 6 } \) = \(\frac{3 \div 3}{6 \div 3}\) = \(\frac { 1 }{ 2 } \)
Shaded part of (iv) = \(\frac { 4 }{ 8 } \) = \(\frac{4 \div 4}{8 \div 4}\) = \(\frac { 1 }{ 2 } \)
Since, \(\frac { 1 }{ 2 } \) = \(\frac { 2 }{ 4 } \) = \(\frac { 3 }{ 6 } \) = \(\frac { 4 }{ 8 } \)
Thus, all the fractions are equivalent.
(b) Fraction represented by,
Shaded part of (i) = \(\frac { 4 }{ 12 } \) = \(\frac{4 \div 4}{12 \div 4}\) = \(\frac { 1 }{ 3 } \)
Shaded part of (ii) = \(\frac { 2 }{ 4 } \) = \(\frac{3 \div 3}{9 \div 3}\) = \(\frac { 1 }{ 2 } \)
Shaded part of (iii) = \(\frac { 3 }{ 6 } \) = \(\frac{2 \div 2}{6 \div 2}\) = \(\frac { 1 }{ 2 } \)
Shaded part of (iv) = \(\frac { 1 }{ 3 } \)
Shaded part of (v) = \(\frac { 6 }{ 15 } \) = \(\frac{6 \div 3}{15 \div 3}\) = \(\frac { 2 }{ 5 } \)
Since, all the fractions do not represent the
same fraction, i.e.
\(\frac { 4 }{ 12 } \) = \(\frac { 3 }{ 9 } \) = \(\frac { 2 }{ 9 } \) = \(\frac { 1 }{ 3 } \) ≠ \(\frac { 2 }{ 5 } \)
The fractions are not equivalent.
![]()
Question 2.
Write the fractions and pair up the equivalent fractions from each row.
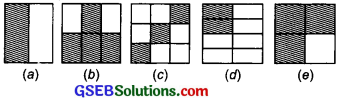

Solution:
Fraction represented by the figure:

Now, the equivalent fractions are:

![]()
Question 3.
Replace ![]() in each of the following by the correct number:
in each of the following by the correct number:

Solution:
(a) We have ![]()
![]() x 2 = 7 x 8
x 2 = 7 x 8
![]() = \(\frac { 7×8 }{ 2 } \) = 28
= \(\frac { 7×8 }{ 2 } \) = 28
![]()
(b) We have \(\frac { 5 }{ 8 } \) = ![]()
5 x ![]() = 10 x 8
= 10 x 8

![]()
Question 4.
Find the equivalent fraction of \(\frac { 3 }{ 5 } \) having
(a) denominator 20
(b) numerator 9
(c) denominator 30
(d) numerator 27
Solution:
Let ‘N’ stands for numerator and ‘D’ stands for the denominator, then
(a) Here, it is required that denominator be 20.
\(\frac { N }{ 20 } \) = \(\frac { 3 }{ 5 } \)
N x 5 = 3 x 20
N = \(\frac { 3 x 20 }{ 5 } \) = 12
(b) Here, it is required that numerator = 9
\(\frac { 9 }{ D } \) = \(\frac { 3 }{ 5 } \)
5 x 9 = 3 x D
D = \(\frac { 5 x 9 }{ 3 } \) = 15
Required fraction = \(\frac { 9 }{ 15 } \)
(e) Here, it is required that denominator = 30
N x 5 = 3 x 30
N = \(\frac { 3 x 30 }{ 5 } \) = 18
Required fraction = \(\frac { 18 }{ 30 } \)
(d) Here, it is required that numerator = 27
\(\frac { 27 }{ D } \) = \(\frac { 3 }{ 5 } \)
= 27 x 5 = 3 x D
D = \(\frac { 27 x 5 }{ 3 } \) = 45
Required fraction = \(\frac { 27 }{ 45 } \)
![]()
Question 5.
Find the equivalent fraction of with
(a) numerator 9
(b) denominator 4
Solution:
(a) Here, it is required that numerator = 9
\(\frac { 9 }{ D } \) = \(\frac { 36 }{ 48 } \)
= 9 x 48 = D x 36
D = \(\frac { 9 x 48 }{ 36 } \) = 12
\(\frac { 9 }{ 12 } \) = \(\frac { 36 }{ 48 } \)
Required fraction = \(\frac { 9 }{ 12 } \)
(b) Here, it is required that denominator = 4
\(\frac { N }{ 4 } \) = \(\frac { 36 }{ 48 } \)
= N x 48 = 4 x 36
N = \(\frac { 4 x 36 }{ 48 } \) = 3
\(\frac { 3 }{ 4 } \) = \(\frac { 36 }{ 48 } \)
Required fraction = \(\frac { 3 }{ 4 } \)
Question 6.
Check whether the given fractions are equivalent:
(a) \(\frac { 5 }{ 9 } \), \(\frac { 30 }{ 54 } \)
(b) \(\frac { 3 }{ 10 } \), \(\frac { 12 }{ 50 } \)
(c) \(\frac { 7 }{ 13 } \), \(\frac { 5 }{ 11 } \)
Solution:
\(\frac { 5 }{ 9 } \) and \(\frac { 30 }{ 54 } \)
We have, 5 x 54 = 30 x 9
Thus, \(\frac { 5 }{ 9 } \) and \(\frac { 30 }{ 54 } \)
(b) \(\frac { 3 }{ 10 } \), \(\frac { 12 }{ 50 } \)
We have, 3 x 50 ≠ 12 x 10
Thus, \(\frac { 3 }{ 10 } \) and \(\frac { 12 }{ 50 } \) are not equivalent fractions.
(c) \(\frac { 7 }{ 13 } \) and \(\frac { 5 }{ 11 } \)
We have, 7 x = 77 and 5 x 13 = 65
7 x 11↑5 x 13
Thus, and – are not equivalent fractions.
![]()
Question 7.
Reduce the following fractions to simplest form.
(a) \(\frac { 48 }{ 60 } \)
(b) \(\frac { 105 }{ 60 } \)
(c) \(\frac { 84 }{ 98 } \)
(d) \(\frac { 12 }{ 52 } \)
(e) \(\frac { 7 }{ 28 } \)
Solution:
\(\frac { 48 }{ 60 } \)
Factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
Factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60
Common factors are: 1, 2, 3, 4, 6 and 12.
HCF of 48 and 60 is 12.
Now, \(\frac{48 \div 12}{60 \div 12}\) = \(\frac { 4 }{ 5 } \)
Thus, the simplest form of \(\frac { 48 }{ 60 } \) is \(\frac { 4 }{ 5 } \)
(b) \(\frac { 150 }{ 60 } \)
We have

HCF of 150 and 60 = 30
Now \(\frac { 150 }{ 60 } \) = \(\frac{150 \div 30}{60 \div 30}\) = \(\frac { 5 }{ 2 } \)
Thus, the simplest form of latex]\frac { 150 }{ 60 } [/latex] is latex]\frac { 5 }{ 2 } [/latex]
(c) latex]\frac { 84 }{ 98 } [/latex]
We have

HCF of 84 and 98 = 14.
Now \(\frac { 84 }{ 98 } \) = \(\frac{84 \div 14}{98 \div 14}\) = \(\frac { 6 }{ 7 } \)
Thus, the simplest form of \(\frac { 84 }{ 98 } \) is \(\frac { 6 }{ 7 } \)
(d) \(\frac { 12 }{ 52 } \)
Factors of 12 are: 1, 2, 3, 4, 6 and 12
Factors of 52 are: 1, 2, 4, 13, 26 and 52
Common factors are: 1, 2 and 4
HCF of 12 and 52 is 4.
Now \(\frac { 12 }{ 52 } \) = \(\frac{12 \div 4}{52 \div 4}\) = \(\frac { 3 }{ 13 } \)
Thus, the simplest form of \(\frac { 12 }{ 52 } \) is \(\frac { 3 }{ 13 } \)
(e) \(\frac { 7 }{ 28 } \)
Factors of 7 are: 1 and 7
Factors of 28 are: 1, 2, 4, 7, 14 and 28
Common factors are: 1 and 7
HCF of 7 and 28 = 7
Now \(\frac { 7 }{ 28 } \) = \(\frac{7 \div 7}{28 \div 7}\) = \(\frac { 1 }{ 4 } \)
Thus, the simplest form of \(\frac { 7 }{ 28 } \) is \(\frac { 1 }{ 4 } \).
![]()
Question 8.
Ramesh had 20 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up ¡0 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each use up? Check if each has used up an equal fraction of her/his pencils?
Solution:
Fraction of pencils used by Ramesh = \(\frac { 10 }{ 20 } \)
Fraction of pencils used by Sheelu = \(\frac { 25 }{ 50 } \)
Fraction of pencils used by Jamaal = \(\frac { 40 }{ 80 } \)
We have \(\frac { 10 }{ 20 } \) = \(\frac{10 \div 10}{20 \div 10}\) = \(\frac { 1 }{ 2 } \)
\(\frac { 25 }{ 50 } \) = \(\frac{25 \div 25}{50 \div 25}\) = \(\frac { 1 }{ 2 } \)
\(\frac { 40 }{ 80 } \) = \(\frac{40 \div 40}{80 \div 40}\) = \(\frac { 1 }{ 2 } \)
Therefore, \(\frac { 10 }{ 20 } \) = \(\frac { 25 }{ 50 } \) = \(\frac { 40 }{ 80 } \)[each \(\frac { 1 }{ 2 } \) ]
Each used up an equal fraction (\(\frac { 1 }{ 2 } \)) of his/her pencils.
Question 9.
Match the equivalent fractions and write two more for each.

Solution:
The fractions (a), (b), (c), (d) and (e) are in simplest form.
We will reduce (i), (ii), (iii), (iv) and (v) into simplest form.
(i) \(\frac { 250 }{ 400 } \)
Factors of 250 =![]()
Factors of 400 = ![]()
HCF of 250 and 400 = 2 x 5 x 5 = 50
Now, \(\frac { 250 }{ 400 } \) = \(\frac{250 \div 50}{400 \div 50}\) = \(\frac { 5 }{ 8 } \)
\(\frac { 250 }{ 400 } \) → \(\frac { 5 }{ 8 } \)
or
(i) → (d)
Two more equivalent fractions:
\(\frac { 5 }{ 8 } \) x \(\frac { 2 }{ 2 } \) = \(\frac { 10 }{ 16 } \) and \(\frac { 5 }{ 8 } \) x \(\frac { 3 }{ 3 } \) = \(\frac { 15 }{ 24 } \)
(ii) \(\frac { 180 }{ 200 } \)
Factors of 180 = ![]()
Factors of 200 = ![]()
Now, \(\frac { 180 }{ 200 } \) = \(\frac{180 \div 20}{200 \div 20}\) = \(\frac { 9 }{ 10 } \)
\(\frac { 180 }{ 200 } \) → \(\frac { 9 }{ 10 } \)
(ii) → (e)
Two more equivalent fractions:
\(\frac { 9 }{ 10 } \) = \(\frac { 2 }{ 2 } \) = \(\frac { 18 }{ 20 } \) and \(\frac { 9 }{ 10 } \) x \(\frac { 3 }{ 3 } \) = \(\frac { 27 }{ 30 } \)
(iii) \(\frac { 660 }{ 990 } \)
Factors of 660 = ![]()
Factors of 990 = ![]()
HCF of 660 and 990
= 2 x 3 x 5 x = 330
Now, \(\frac { 660 }{ 990 } \) = \(\frac{660 \div 330}{990 \div 330}\) = \(\frac { 2 }{ 3 } \)
\(\frac { 660 }{ 990 } \) → \(\frac { 2 }{ 3 } \)
or
(iii) → (a)
Two more equivalent fractions are:
\(\frac { 2 }{ 3 } \) x \(\frac { 2 }{ 2 } \) = \(\frac { 4 }{ 6 } \) and \(\frac { 2 }{ 3 } \) x \(\frac { 3 }{ 3 } \) = \(\frac { 6 }{ 9 } \)
(iv) \(\frac { 180 }{ 360 } \)
Factors of 180 =2 x 2 x 3 x 3 x 5
Factors of 360 = 2 x 2 x 3 x 3 x 5 x 2
HCF of 180 and 360
= 2 x 2 x 3 x 3 x 5 = 180
Now, \(\frac { 180 }{ 360 } \) = \(\frac{180 \div 180}{360 \div 180}\) = \(\frac { 1 }{ 2 } \)
\(\frac { 180 }{ 360 } \) → \(\frac { 1 }{ 2 } \)
or
(iv) → (a)
Two more equivalent fractions:
\(\frac { 1 }{ 2 } \) x \(\frac { 2 }{ 2 } \) = \(\frac { 2 }{ 4 } \) and \(\frac { 1 }{ 2 } \) x \(\frac { 3 }{ 3 } \) = \(\frac { 3 }{ 6 } \)
(v) \(\frac { 220 }{ 550 } \)
We have, Factors of 220 = ![]()
Factors of 550 = ![]()
HCF of 220 and 550 = 2 x 5 x 11 = 110
Now, \(\frac { 220 }{ 550 } \) = \(\frac{220 \div 110}{550 \div 110}\) = \(\frac { 2 }{ 5 } \)
\(\frac { 220 }{ 550 } \) → \(\frac { 2 }{ 5 } \)
or
(v) → (b)
Two more equivalent fractions:
\(\frac { 2 }{ 5 } \) x \(\frac { 2 }{ 5 } \) = \(\frac { 4 }{ 10 } \) and \(\frac { 2 }{ 5 } \) x \(\frac { 3 }{ 3 } \) = \(\frac { 6 }{ 15 } \)
![]()