Gujarat Board GSEB Solutions Class 6 Maths Chapter 7 અપૂર્ણાંક સંખ્યાઓ Ex 7.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 7 અપૂર્ણાંક સંખ્યાઓ Ex 7.3
પ્રશ્ન 1.
અપૂર્ણાંક સ્વરૂપે લખો. શું આ બધા સમઅપૂર્ણાકો છે?
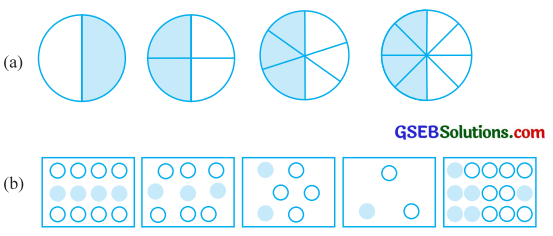
જવાબ:
(a)
(i) ચિત્રમાંના કુલ સરખા ભાગ = 2
આમાંથી છાયાંકિત ભાગ = 1
![]()
(ii) ચિત્રમાંના કુલ સરખા ભાગ = 4. આમાંથી છાયાંકિત ભાગ = 2
છાયાંકિત ભાગ
![]()
(iii) ચિત્રમાંના કુલ સરખા ભાગ = 6
આમાંથી છાયાંકિત ભાગ = 3
![]()
(iv) ચિત્રમાંના કુલ સરખા ભાગ = 8
આમાંથી છાયાંકિત ભાગ = 4
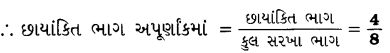
ઉપરના અપૂર્ણાકોને અતિસંક્ષિપ્ત સ્વરૂપમાં ફેરવીએઃ
\(\frac{2}{4}\) = \(\frac{2 \div 2}{4 \div 2}\) = \(\frac{1}{2}\) [∵ 2 અને 4નો ગુ.સા.અ. 2 છે.]
\(\frac{3}{6}\) = \(\frac{3 \div 3}{6 \div 3}\) = \(\frac{1}{2}\) [∵ 3 અને 6નો ગુ.સા.અ. 3 છે.]
\(\frac{4}{8}\) = \(\frac{4 \div 4}{8 \div 4}\) = \(\frac{1}{2}\) [∵ 4 અને 8નો ગુ.સા.અ. 4 છે.]
![]()
(b)
(i) ચિત્રમાંના કુલ સરખા ભાગ = 12
આમાંથી છાયાંકિત ભાગ = 4
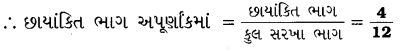
(ii) ચિત્રમાંના કુલ સરખા ભાગ = 9
આમાંથી છાયાંકિત ભાગ = 3.
![]()
(iii) ચિત્રમાંના કુલ સરખા ભાગ = 6
આમાંથી છાયાંકિત ભાગ = 2.
![]()
(iv) ચિત્રમાંના કુલ સરખા ભાગ = 15
આમાંથી છાયાંકિત ભાગ = 6
![]()
(v) ચિત્રમાંના કુલ સરખા ભાગ = 15
આમાંથી છાયાંકિત ભાગ = 6
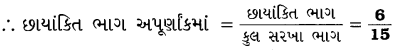
આગળના અપૂર્ણાકોને અતિસંક્ષિપ્ત સ્વરૂપમાં ફેરવીએ:
\(\frac{4}{12}\) = \(\frac{4 \div 4}{12 \div 4}\) = \(\frac{1}{3}\) [∵ 4 અને 12નો ગુ.સા.અ. 4 છે.]
\(\frac{3}{9}\) = \(\frac{3 \div 3}{9 \div 3}\) = \(\frac{1}{3}\) [∵ 3 અને 9નો ગુ.સા.અ. 3 છે.]
\(\frac{2}{6}\) = \(\frac{2 \div 2}{6 \div 2}\) = \(\frac{1}{3}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\)
\(\frac{6}{15}\) = \(\frac{6 \div 3}{15 \div 3}\) = \(\frac{2}{5}\)
[∵ 6 અને 15નો ગુ.સા.અ. 3 છે.]
આમ, \(\frac{4}{12}\) = \(\frac{3}{9}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\) ≠ \(\frac{6}{5}\).
∴ ના, બધા અપૂર્ણાંકો સમઅપૂર્ણાંકો નથી.
પ્રશ્ન 2.
અપૂર્ણાંક લખો અને દરેક હરોળની સમઅપૂર્ણાકની જોડ લખો:
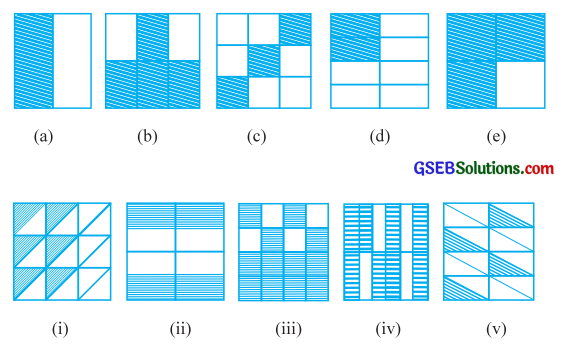
જવાબ :
ઉપરના દાખલામાં જોયું તે પ્રમાણે દરેકમાં નીચેના સૂત્રનો ઉપયોગ કરી અપૂર્ણાંક શોધીશું:
![]()
(a) \(\frac{1}{2}\) = \(\frac{1}{2}\)
(b) \(\frac{4}{6}\) = \(\frac{2}{3}\)
(c) \(\frac{3}{9}\) = \(\frac{1}{3}\)
(d) \(\frac{2}{8}\) = \(\frac{1}{4}\)
(e) \(\frac{3}{4}\) = \(\frac{3}{4}\)
(i) \(\frac{6}{18}\) = \(\frac{1}{3}\)
(ii) \(\frac{4}{8}\) = \(\frac{1}{2}\)
(iii) \(\frac{12}{16}\) = \(\frac{3}{4}\)
(iv) \(\frac{8}{12}\) = \(\frac{2}{3}\)
(v) \(\frac{4}{16}\) = \(\frac{1}{4}\)
હવે, સમઅપૂર્ણાકો નીચે પ્રમાણે છે :
(a) → (ii) [∵ \(\frac{1}{2}\) = \(\frac{1}{2}\)
(b) → (iv) [∵ \(\frac{2}{3}\) = \(\frac{2}{3}\)
(c) → (i) [∵ \(\frac{1}{3}\) = \(\frac{1}{3}\)
(d) → (v) [∵ \(\frac{1}{4}\) = \(\frac{1}{4}\)
(e) → (iii) [∵ \(\frac{3}{4}\) = \(\frac{3}{4}\)
પ્રશ્ન 3.
નીચે આપેલા દરેકના ![]() માં સાચી સંખ્યા મૂકો
માં સાચી સંખ્યા મૂકો
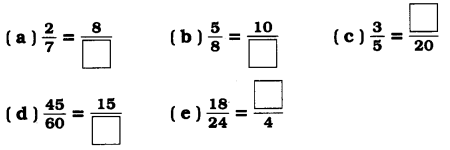
જવાબ :

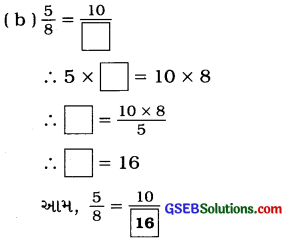
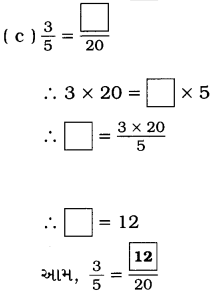

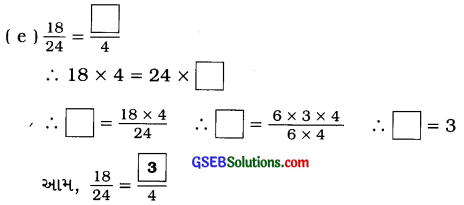
પ્રશ્ન 4.
\(\frac{3}{5}\)નો સમઅપૂર્ણાંક શોધો કે જેનો –
(a) છેદ 20
(b) અંશ 9
(c) છેદ 30
(d) અંશ 27
જવાબ:
અહીં, આપણે અંશ માટે A અને છેદ માટે B ધારીશું.
(a) જેનો છેદ 20 હોય તેવો \(\frac{3}{5}\)નો સમઅપૂર્ણાક \(\frac{A}{20}\) છે.
∴ \(\frac{A}{20}\) = \(\frac{3}{5}\)
∴ A × 5 = 3 × 20 ∴ A = \(\frac{3 \times 20}{5}\) ∴ A = 12
આમ, માગેલો અપૂર્ણાંક \(\frac{12}{20}\) છે.
(b) જેનો અંશ છુ હોય તેવો \(\frac{3}{5}\)નો સમઅપૂર્ણાક \(\frac{9}{B}\)છે.
∴ \(\frac{9}{B}\) = \(\frac{3}{5}\)
∴ 9 × 5 = 3 × B ∴ B = \(\frac{9 \times 5}{3}\) ∴ B = 15
આમ, માગેલો અપૂર્ણાક \(\frac{9}{15}\)છે.
(c) જેનો છેદ 30 હોય તેવો \(\frac{3}{5}\)નો સમઅપૂર્ણાંક \(\frac{A}{30}\) છે.
∴ \(\frac{A}{30}\) = \(\frac{3}{5}\)
∴ A × 5 = 3 × 30
∴ A = \(\frac{3 \times 30}{5}\) ∴ A = \(\frac{3 \times 5 \times 6}{5}\) ∴ A = 3 × 6 ∴ A = 18
આમ, માગેલો અપૂર્ણાંક \(\frac{18}{30}\) છે.
(d) જેનો અંશ 27 હોય તેવો નો સમઅપૂર્ણાંક \(\frac{27}{B}\) છે.
∴\(\frac{27}{B}\) = \(\frac{3}{5}\)
∴ 27 × 5 = 3 × B
∴ B = \(\frac{27 \times 5}{3}\) ∴ B = \(\frac{3 \times 9 \times 5}{3}\) ∴ B = 45
આમ, માગેલો અપૂર્ણાંક \(\frac{27}{45}\) છે.
![]()
પ્રશ્ન 5.
\(\frac{36}{48}\)નો સમઅપૂર્ણાંક શોધો કે જેનો –
(a) છેદ 20
(b) અંશ 9
જવાબ:
(a) જેનો અંશ 9 હોય તેવો \(\frac{36}{48}\)ના સમઅપૂર્ણાકનો છેદ B ધારીએ.
∴ \(\frac{9}{B}\) = \(\frac{36}{48}\)
∴ 9 × 48 = 36 × B
∴ B = \(\frac{9 \times 48}{36}\) ∴ B = \(\frac{3 \times 3 \times 4 \times 12}{4 \times 3 \times 3}\) ∴ B = 12
આમ, \(\frac{9}{12}\) = \(\frac{36}{48}\)
∴ માગ્યા મુજબનો અપૂર્ણાંક \(\frac{9}{12}\) છે.
(b)જેનો છેદ 4 હોય તેવો \(\frac{36}{48}\)૬ના સમઅપૂર્ણાકનો અંશ A ધારીએ.
∴ \(\frac{A}{4}\) = \(\frac{36}{48}\)
∴ A × 48 = 36 × 4
∴ A = \(\frac{36 \times 4}{48}\) ∴ A = \(\frac{12 \times 3 \times 4}{12 \times 4}\) ∴ A = 3
આમ, \(\frac{3}{4}\) =\(\frac{36}{48}\)
∴ માગ્યા મુજબનો અપૂર્ણાંક \(\frac{3}{4}\) છે.
પ્રશ્ન 6.
આપેલ અપૂર્ણાકો સમાન છે કે નથી, એ ચકાસોઃ
(a) \(\frac{5}{9}\), \(\frac{30}{54}\)
(b) \(\frac{3}{10}\), \(\frac{12}{50}\)
(c) \(\frac{7}{13}\), \(\frac{5}{11}\)
જવાબ:
(a) \(\frac{5}{9}\), \(\frac{30}{54}\)
જો \(\frac{5}{9}\) અને \(\frac{30}{54}\) એ સમાન અપૂર્ણાંક હોય, તો 5 × 54 = 30 × 9 થવા જોઈએ.
5 × 54 = 270 તથા 30 × 9 = 270
∴ \(\frac{5}{9}\) અને \(\frac{30}{54}\) એ સમાન અપૂર્ણાંક છે.
(b) \(\frac{3}{10}\), \(\frac{12}{50}\)
જો \(\frac{3}{10}\) અને \(\frac{12}{50}\) એ સમાન અપૂર્ણાંક હોય, તો 3 × 50 = 12 × 10 થવા જોઈએ.
‘3 × 50 = 150 તથા 10 × 18 = 120 અહીં, 150 ≠ 120
∴ \(\frac{3}{10}\) અને \(\frac{12}{50}\) એ સમાન અપૂર્ણાંક નથી.
(c) \(\frac{7}{13}\), \(\frac{5}{11}\)
જો \(\frac{7}{13}\) અને \(\frac{5}{11}\) એ સમાન અપૂર્ણાંક હોય, તો 7 × 11 = 5 × 13 થવા જોઈએ.
7 × 11 = 77 તથા 5 × 18 = 65 અહીં, 77 ≠ 65
∴ \(\frac{7}{11}\) અને \(\frac{5}{11}\) એ સમાન અપૂર્ણાંક નથી.
પ્રશ્ન 7.
નીચે આપેલા અપૂર્ણાકોને તેના અતિસંક્ષિપ્ત સ્વરૂપમાં ફેરવોઃ
(a) \(\frac{48}{60}\)
(b) \(\frac{150}{60}\)
(c) \(\frac{84}{98}\)
(d) \(\frac{12}{52}\)
(e) \(\frac{7}{28}\)
જવાબઃ
(a) \(\frac{48}{60}\)
48ના અવિભાજ્ય અવયવો 2, 2, 2, 2, 3 છે.
60ના અવિભાજ્ય અવયવો 2, 2, 3, 5 છે.
48 અને 60ના સામાન્ય અવિભાજ્ય અવયવો 2, 2, 3
∴ 48 અને 60નો ગુ.સા.અ. = 2 × 2 × 3 = 12
હવે, \(\frac{48}{60}\) = \(\frac{48 \div 12}{60 \div 12}\) = \(\frac{4}{5}\)
આમ, \(\frac{48}{60}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{4}{5}\) છે.
(b) \(\frac{150}{60}\)
150ના અવિભાજ્ય અવયવો : 2, 3, 5, 5 છે.
60ના અવિભાજ્ય અવયવો : 2, 2, 3, 5 છે.
150 અને 60ના સામાન્ય અવિભાજ્ય અવયવો : 2, 3, 5
∴ 150 અને 60નો ગુ.સા.અ. = 2 × 3 × 5 = 30
હવે. \(\frac{150}{60}\) = \(\frac{150 \div 30}{60 \div 30}\) = \(\frac{5}{2}\)
આમ, \(\frac{150}{60}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{5}{2}\) છે.
(c) \(\frac{84}{98}\)
84નો અવિભાજ્ય અવયવો : 2, 2, 3, 7 છે.
98ના અવિભાજ્ય અવયવો 2, 7, 7 છે.
84 અને 98ના સામાન્ય અવિભાજ્ય અવયવો: 2, 7
∴ 84 અને 98નો ગુ.સા.અ. = 2 × 7 = 14
હવે, \(\frac{84}{98}\) = \(\frac{84 \div 14}{98 \div 14}\) = \(\frac{6}{7}\)
આમ, \(\frac{84}{98}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{6}{7}\) છે.
(d) \(\frac{12}{52}\)
12ના અવિભાજ્ય અવયવો 2, 2, 3 છે.
52ના અવિભાજ્ય અવયવો 2, 2, 13 છે.
12 અને 52ના સામાન્ય અવિભાજ્ય અવયવો : 2, 2
12 અને 52નો ગુ.સા.અ. = 2 × 2 = 4
હવે, \(\frac{12}{52}\) = \(\frac{12 \div 4}{52 \div 4}\) = \(\frac{3}{13}\)
આમ, \(\frac{12}{52}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{3}{13}\) છે.
(e) \(\frac{7}{28}\)
7નો અવિભાજ્ય અવયવ : 7 છે.
28ના અવિભાજ્ય અવયવો : 2, 2, 7 છે.
7 અને 28નો સામાન્ય અવિભાજ્ય અવયવ : 7
∴ 7 અને 28નો ગુ.સા.અ. = 7
હવે, \(\frac{7}{28}\) = \(\frac{7 \div 7}{28 \div 7}\) = \(\frac{1}{4}\)
આમ, \(\frac{7}{28}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{1}{4}\) છે.
![]()
પ્રશ્ન 8.
રમેશ પાસે 20 પેન્સિલ છે. શીલુ પાસે 50 પેન્સિલ છે. જમાલ પાસે 80 પેન્સિલ છે. 4 મહિના પછી રમેશે 10 પેન્સિલનો ઉપયોગ કરી લીધો. શીલુએ 25 પેન્સિલનો અને જમાલે 40 પેન્સિલનો ઉપયોગ કર્યો. દરેકે કેટલામા ભાગનો ઉપયોગ કર્યો? ચકાસો તેઓએ પેન્સિલનો સરખા ભાગનો ઉપયોગ કર્યો?
જવાબઃ
અહીં, રમેશ વડે વપરાયેલ કુલ પેન્સિલનો ભાગ = \(\frac{10}{20}\)
શીલુ વડે વપરાયેલ કુલ પેન્સિલનો ભાગ = \(\frac{25}{50}\)
જમાલ વડે વપરાયેલ કુલ પેન્સિલનો ભાગ = \(\frac{40}{80}\)
હવે, \(\frac{10}{20}\) = \(\frac{10 \div 10}{20 \div 10}\) = \(\frac{1}{2}\) [∵ 10 અને 20નો ગુ.સા.અ. 10 છે.]
\(\frac{25}{50}\) = \(\frac{25 \div 25}{50 \div 25}\) = \(\frac{1}{2}\) [∵ 25 અને 50નો ગુ.સા.અ. 25 છે.]
\(\frac{40}{80}\) = \(\frac{40 \div 40}{80 \div 40}\) = \(\frac{1}{2}\) [∵ 40 અને 80નો ગુ.સા.અ. 40 છે.]
આમ, \(\frac{10}{20}\) = \(\frac{25}{50}\) = \(\frac{40}{80}\) = \(\frac{1}{2}\) છે.
∴ હા, બધાંએ કુલ પેન્સિલનો એકસરખા ભાગ(\(\frac{1}{2}\) ભાગ))નો ઉપયોગ કર્યો છે.
પ્રશ્ન 9.
સમઅપૂર્ણાકોની જોડ બનાવો અને દરેકનાં બીજાં બે ઉદાહરણ લખોઃ
(i) \(\frac{250}{400}\) (a) \(\frac{2}{3}\)
(ii) \(\frac{180}{400}\) (b) \(\frac{2}{5}\)
(iii) \(\frac{660}{990}\) (c) \(\frac{1}{2}\)
(iv) \(\frac{180}{360}\) (d) \(\frac{5}{8}\)
(v) \(\frac{220}{400}\) (e) \(\frac{9}{10}\)
જવાબ :
અહીં, આપેલા અપૂર્ણાકોને તેમના અતિસંક્ષિપ્ત સ્વરૂપમાં ફેરવીએ.
(i) \(\frac{250}{400}\)
250ના અવિભાજ્ય અવયવો 2, 5, 6, 5 છે.
400ના અવિભાજ્ય અવયવો 2, 2, 2, 2, 5, 5
250 અને 400ના સામાન્ય અવિભાજ્ય અવયવો 2, 5, 5
∴ 250 અને 400નો ગુ.સા.અ. = 2 × 5 × 5 = 50
હવે, \(\frac{250}{400}\) = \(\frac{250 \div 50}{400 \div 50}\) = \(\frac{5}{8}\)
આમ, જોડકામાં (i) → (d)
\(\frac{5}{8}\)ના બીજા બે સમઅપૂર્ણાકો: \(\frac{5 \times 2}{8 \times 2}\) = \(\frac{10}{16}\) તથા \(\frac{5 \times 3}{8 \times 3}\) = \(\frac{15}{24}\)
(ii) \(\frac{180}{200}\)
180ના અવિભાજ્ય અવયવો 2, 2, 3, 3, 5
200ના અવિભાજ્ય અવયવો 2, 2, 2, 5, 5
180 અને 200ના સામાન્ય અવિભાજ્ય અવયવો 2, 2, 5
∴ 180 અને 200નો ગુ.સા.અ. = 2 × 2 × 5 = 20
હવે, \(\frac{180}{200}\) = \(\frac{180 \div 2}{200 \div 2}\) = \(\frac{9}{10}\)
આમ, જોડકામાં (ii) → (e).
\(\frac{9}{10}\)ના બીજા બે સમઅપૂણકો: \(\frac{9 \times 2}{10 \times 2}\) = \(\frac{18}{20}\) તથા \(\frac{9 \times 3}{10 \times 3}\) = \(\frac{27}{30}\)
(iii) \(\frac{660}{990}\)
660ના અવિભાજ્ય અવયવો: 2, 2, 3, 5, 11
990ના અવિભાજ્ય અવયવો 2, 3, 3, 5, 11
660 અને 990ના સામાન્ય અવિભાજ્ય અવયવો 2, 3, 5, 11
∴ 660 અને 990નો ગુ.સા.અ. = 2 × 3 × 5 × 11 = 330
હવે \(\frac{660}{990}\) = \(\frac{660 \div 330}{990 \div 330}\) = \(\frac{2}{3}\)
આમ, જોડકામાં (iii) → (a)
\(\frac{2}{3}\)ના બીજા બે સમઅપૂર્ણાકો: \(\frac{2 \times 2}{3 \times 2}\) = \(\frac{4}{6}\) તથા \(\frac{2 \times 3}{3 \times 3}\) = \(\frac{6}{9}\)
(iv) \(\frac{180}{360}\)
180ના અવિભાજ્ય અવયવો : 2, 2, 3, 3, 5
360ના અવિભાજ્ય અવયવો : 2, 2, 2, 3, 3, 5
180 અને 360ના સામાન્ય અવિભાજ્ય અવયવો : 2, 2, 3, 3, 5
∴ 180 અને 360નો ગુ.સા.અ. = 2 × 2 × 3 × 3 × 5 = 180
હવે \(\frac{180}{360}\) = \(\frac{180 \div 180}{360 \div 180}\) = \(\frac{1}{2}\)
આમ, જોડકામાં (iv) → (c).
\(\frac{1}{2}\)ના બીજા બે સમઅપૂર્ણાકો \(\frac{1 \times 2}{2 \times 2}\) = \(\frac{2}{4}\) તથા \(\frac{1 \times 2}{2 \times 2}\) = \(\frac{3}{6}\)
(v) \(\frac{220}{550}\)
220ના અવિભાજ્ય અવયવો 2, 2, 5, 11
550ના અવિભાજ્ય અવયવો: 2, 5, 6, 11
220 અને 550ના સામાન્ય અવિભાજ્ય અવયવો 2, 5, 11
∴ 220 અને 550નો ગુ.સા.અ. = 2 × 5 × 11 = 110
હવે, \(\frac{220}{550}\) = \(\frac{220 \div 110}{550 \div 110}\) = \(\frac{2}{5}\)
આમ, જોડકામાં (v) → (b)
∴ \(\frac{2}{5}\)ના બીજા બે સમઅપૂર્ણાકો: \(\frac{2 \times 2}{5 \times 2}\) = \(\frac{4}{10}\) તથા \(\frac{2 \times 3}{5 \times 3}\) = \(\frac{6}{15}\)