Gujarat Board GSEB Solutions Class 6 Maths Chapter 8 દશાંશ સંખ્યાઓ Ex 8.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 8 દશાંશ સંખ્યાઓ Ex 8.1
પ્રશ્ન 1.
નીચે આપેલ કોષ્ટકમાં સંખ્યા લખો:
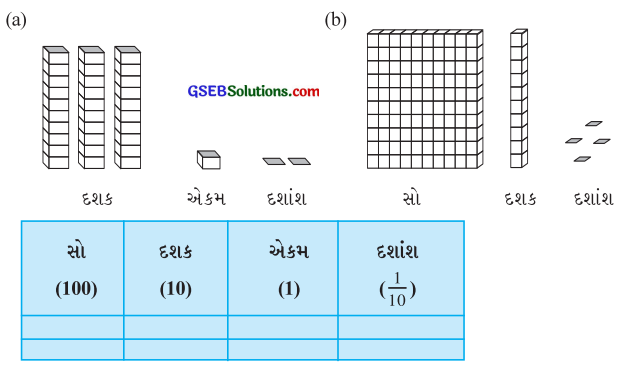
જવાબ:
(a) અહીં આપેલા ચિત્રમાં દશકના સ્થાનમાં 3 સ્તંભ (દરેક 10 એકમનો), એકમના સ્થાનમાં 1 બ્લૉક તથા દશાંશના સ્થાનમાં 2 ભાગ (દરેક એક દશાંશનો) છે. આથી, આપેલ કોષ્ટક નીચે પ્રમાણે દર્શાવી શકાય:
આમ, સંખ્યા 31.2
![]()
(b) અહીં આપેલા ચિત્રમાં સોના સ્થાનમાં 1 સ્તંભ (દરેક 100 એકમનો), દશકના સ્થાનમાં 1 ખંભ (દરેક 10 એકમનો), એકમના સ્થાનમાં કોઈ બ્લૉક નથી તથા દશાંશના સ્થાનમાં 4 ભાગ (દરેક એક દશાંશનો) છે. આથી, આપેલ કોષ્ટક નીચે પ્રમાણે દર્શાવી શકાય:

આમ, સંખ્યા : 110.4
પ્રશ્ન 2.
નીચેની દશાંશ સંખ્યાઓને સ્થાનકિંમતના કોષ્ટકમાં લખો
(a) 19.4
(b) 0.3
(c) 10.6
(d) 205.9
જવાબ:
(a) 19.4
19.4 = 1 × 10 + 9 × 1 + 4 × \(\frac{1}{10}\)
હવે, સ્થાનકિંમતના કોષ્ટકમાં તેને દર્શાવીએ.
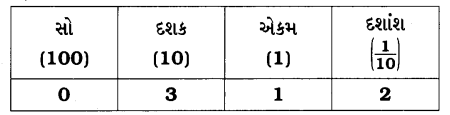
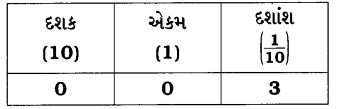
(b) 0.3
0.3 = 0 × 10 + 0 × 1 + 3 × \(\frac{1}{10}\)
હવે, સ્થાનકિંમતના કોષ્ટકમાં તેને દર્શાવીએ.
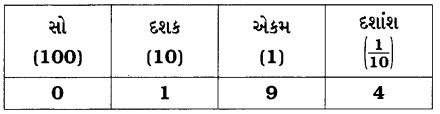
(c) 10.6.
10.6 = 1 × 10 + 0 × 1 + 6 × \(\frac{1}{10}\)
હવે, સ્થાનકિંમતના કોષ્ટકમાં તેને દર્શાવીએ.
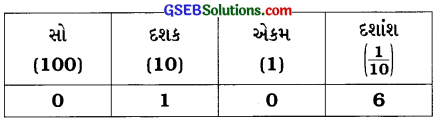
(d) 205.9
205.9 = 2 × 100 + 0 × 10 + 5 × 1 + 9 × \(\frac{1}{10}\)
હવે, સ્થાનકિંમતના કોષ્ટકમાં તેને દર્શાવીએ.
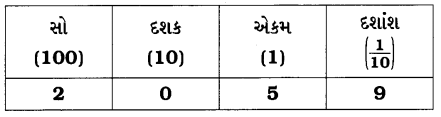
![]()
પ્રશ્ન 3.
નીચેના દરેકને દશાંશ સ્વરૂપે લખો:
(a) સાત દશાંશ
(b) બે દશક અને નવ દશાંશ
(c) ચૌદ પૉઈન્ટ છ
(d) એક સો અને બે એકમ
(e) છસો પૉઇન્ટ આઠ
જવાબ:
(a) સાત દશાંશ
સાત દશાંશ = 7 × \(\frac{1}{10}\)
= 0.7
(b) બે દશક અને નવ દશાંશ
બે દશક અને નવ દશાંશ = 2 × 10 × 9 × \(\frac{1}{10}\)
= 20 + \(\frac{9}{10}\)
= 20 + 0.9
= 20.9
(c) ચૌદ પૉઈન્ટ છે
ચૌદ પૉઈન્ટ છ = 14.6
(d) એક સો અને બે એકમ
એક સો અને બે એકમ = 1 સો + 0 દશક + 2 એકમ + 0 દશાંશ
= 100 + 0 + 2 + \(\frac{0}{10}\)
= 102.0
(e) છસો પૉઈન્ટ આઠ
છસો પૉઈન્ટ આઠ = 600.8
![]()
પ્રશ્ન 4.
નીચેના દરેકને દશાંશ સ્વરૂપે લખો :
(a) \(\frac{5}{10}\)
(b) 3 + \(\frac{7}{10}\)
(c) 200 + 60 + 5 + \(\frac{1}{10}\)
(d) 70 + \(\frac{8}{10}\)
(e) \(\frac{88}{10}\)
(f) 4 \(\frac{2}{10}\)
(h) \(\frac{2}{5}\)
(i) \(\frac{12}{5}\)
(j) 3 \(\frac{3}{5}\)
(k) 4 \(\frac{1}{2}\)
જવાબ:
(a) \(\frac{5}{10}\) = 0.5
(b) 3 + \(\frac{7}{10}\) = 3 + 0.7 = 3.7
(c) 200 + 60 + 5 + \(\frac{1}{10}\) = 265 + 0.1 = 265.1
(d) 70 + \(\frac{8}{10}\) = 70 + 0.8 = 70.8
(e) \(\frac{88}{10}=\frac{80+8}{10}=\frac{80}{10}+\frac{8}{10}=8+\frac{8}{10}\) = 8.8
(f) 4 \(\frac{2}{10}\) = 4 + \(\frac{2}{10}\) = 4.2
(g) \(\frac{3}{2}=\frac{3 \times 5}{2 \times 5}=\frac{15}{10}=\frac{10+5}{10}=\frac{10}{10}+\frac{5}{10}=1+\frac{5}{10}\) = 1.5
(h) \(\frac{2}{5}=\frac{2 \times 2}{5 \times 2}=\frac{4}{10}\) = 0.4
(i) \(\frac{12}{5}=\frac{12 \times 2}{5 \times 2}=\frac{24}{10}=\frac{20+4}{10}=\frac{20}{10}+\frac{4}{10}=2+\frac{4}{10}\) = 2.4
(j) \(3 \frac{3}{5}=3+\frac{3}{5}=3+\left(\frac{3 \times 2}{5 \times 2}\right)=3+\frac{6}{10}\) = 3.6
(k) \(4 \frac{1}{2}=4+\frac{1}{2}=4+\left(\frac{1 \times 5}{2 \times 5}\right)=4+\frac{5}{10}\) = 4.5
![]()
પ્રશ્ન 5.
નીચેની દશાંશ સંખ્યાઓને અપૂર્ણાંક સ્વરૂપમાં લખી સરળ સ્વરૂપમાં ફેરવોઃ
(a) 0.6
(b)2.5
(c) 1.0
(d) 3.8
(e) 13.7
(f) 21.2
(g) 6.4
જવાબઃ
આપેલી દશાંશ સંખ્યાને તેના છેદમાં 10 આવે તે રીતે અપૂર્ણાંકમાં લખીશું. તે પછી અપૂર્ણાંકને સરળ સ્વરૂપમાં ફેરવીશું.
(a) 0.6
0.6 = \(\frac{6}{10}\)
હવે, \(\frac{6}{10}\) = \(\frac{6 \div 2}{10 \div 2}\) = \(\frac{3}{5}\) [∵ 6 અને 10નો ગુ.સા.અ. 2 છે.]
(b) 2.5
2.5 = \(\frac{25}{10}\)
હવે, \(\frac{25}{10}\) = \(\frac{25 \div 5}{10 \div 5}\) = \(\frac{5}{2}\) [∵ 25 અને 10નો ગુ.સા.અ. 5 છે.]
(c) 1.0
1.0 = 1 + \(\frac{0}{10}\) = 1 + 0 = 1
હવે, 1 એ સરળ સ્વરૂપમાં છે જ.
(d) 3.8
3.8 = \(\frac{38}{10}\)
હવે, \(\frac{38}{10}\) = \(\frac{38 \div 2}{10 \div 2}\) = \(\frac{19}{5}\)
![]()
(e) 13.7
13.7 = \(\frac{137}{10}\)
(f) 21.2
21.2 = \(\frac{212}{10}\)
હવે, \(\frac{212}{10}\) = \(\frac{212 \div 2}{10 \div 2}\) [∵ 212 અને 10નો ગુ.સા.અ. 2 છે.]
= \(\frac{106}{5}\)
(g) 6.4
6.4 = \(\frac{64}{10}\)
હવે, \(\frac{64}{10}\) = \(\frac{64 \div 2}{10 \div 2}\) = \(\frac{32}{5}\) [∵ 64 અને 10નો ગુ.સા.અ. 2 છે.]
પ્રશ્ન 6.
દશાંશનો ઉપયોગ કરી, નીચેના દરેકને સેમીમાં દર્શાવોઃ
(a) 2 મિમી
(b) 30 મિમી
(c) 116 મિમી
(d) 4 સેમી 2 મિમી
(e) 162 મિમી
(f) 83 મિમી
જવાબ:
(a) 2 મિમી
10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = 3 સેમી
∴ 2 મિમી = 2 × \(\frac{1}{10}\) સેમી = \(\frac{2}{10}\) સેમી = 0.2 સેમી
(b) 30 મિમી
10 મિમી = 1 સેમી થાય. ∴1 મિમી = 3 સેમી
∴ 30 મિમી = 30 × \(\frac{1}{10}\) સેમી = \(\frac{30}{10}\) સેમી = 3 સેમી
![]()
(c) 116 મિમી
10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = b સેમી
∴ 116 મિમી = 116 × \(\frac{1}{10}\) સેમી = \(\frac{116}{10}\) સેમી
હવે, \(\frac{116}{10}\) સેમી = (\(\frac{116}{10}\) + \(\frac{6}{10}\)) સેમી = (11 + \(\frac{6}{10}\)) સેમી
= 11.6 સેમી
(d) 4 સેમી 2 મિમી
10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = \(\frac{1}{10}\) સેમી
∴ 4 સેમી 2 મિમી = 4 સેમી + 2 × \(\frac{1}{10}\) સેમી
= 4 સેમી + \(\frac{2}{10}\) સેમી
= (4 + 0.2) સેમી = 4.2 સેમી
(e) 162 મિમી
10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = \(\frac{1}{10}\) સેમી
\(\frac{1}{10}\) 162 મિમી = 162 × \(\frac{1}{10}\) સેમી = \(\frac{162}{10}\) સેમી
હવે, \(\frac{162}{10}\) સેમી = (\(\frac{162}{10}\) + \(\frac{2}{10}\)) સેમી = (16 + 0.2) સેમી
= 16.2 સેમી
(f) 83 મિમી
10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = \(\frac{1}{10}\) સેમી
∴ 83 મિમી = 83 × \(\frac{1}{10}\) સેમી = \(\frac{83}{10}\) સેમી
હવે, \(\frac{83}{10}\) સેમી = (\(\frac{80+3}{10}\)) સેમી
= (\(\frac{80}{10}\) + \(\frac{3}{10}\)) સેમી
= (8 + 0.3) સેમી
= 8.૩ સેમી
પ્રશ્ન 7.
સંખ્યારેખા પર કઈ બે પૂર્ણ સંખ્યાઓની વચ્ચે નીચેની સંખ્યાઓનો સમાવેશ થશે? કઈ પૂર્ણ સંખ્યા આપેલ દશાંશ સંખ્યાની નજીક છે?

(a) 0.8
(b) 5.1
(c) 2.6
(d) 6.4
(e) 9.1
(f) 49
જવાબ:
(a) 0.8
0.8 એ 0 અને 1ની વચ્ચે આવેલ છે.
0.8 એ 1ની વધુ નજીક છે.
![]()
(b) 5.1
5.1 એ 5 અને 6ની વચ્ચે આવેલ છે.
5.1 એ 5ની વધુ નજીક છે.
(c) 2.6
2.6 એ 2 અને 3ની વચ્ચે આવેલ છે.
2.6 એ 3ની વધુ નજીક છે.
(d) 6.4
6.4 એ 6 અને 7ની વચ્ચે આવેલ છે.
6.4 એ 6ની વધુ નજીક છે.
(e) 9.1
9.1 એ 9 અને 10ની વચ્ચે આવેલ છે.
9.1 એ 9ની વધુ નજીક છે.
(f) 4.9
4.9 એ 4 અને 5ની વચ્ચે આવેલ છે.
4.9 એ 5ની વધુ નજીક છે.
પ્રશ્ન 8.
નીચેની સંખ્યાઓને સંખ્યારેખા પર દર્શાવો:
(a) 0.2
(b) 1.9
(c) 1.1
(d) 2.5
જવાબ:
(a) 0.2
એ સ્પષ્ટ છે કે 0.2 એ 0 અને 1ની વચ્ચે છે.
હવે, સંખ્યારેખા ઉપર 0થી 1ની વચ્ચે 10 સરખા ભાગ પાડો. સંખ્યારેખા ઉપર આમાંના પહેલા બે ભાગ લો. બિંદુ A એ 0.2ને સંગત બિંદુ છે.
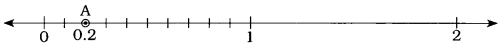
![]()
(b) 1.9.
એ સ્પષ્ટ છે કે 1.9 એ 1 અને 2ની વચ્ચે છે.
હવે, સંખ્યારેખા ઉપર 1 અને 2ની વચ્ચે 10 સરખા ભાગ પાડો. સંખ્યારેખા ઉપર આમાંના પહેલા નવ ભાગ લો. બિંદુ B એ 1.9ને સંગત બિંદુ છે.

(c) 1.1
એ સ્પષ્ટ છે કે 1.1 એ 1 અને 2ની વચ્ચે છે.
હવે, સંખ્યારેખા ઉપર 1 અને 2ની વચ્ચે 10 સરખા ભાગ પાડો. સંખ્યારેખા ઉપર આમાંનો પહેલો ભાગ લો. બિંદુ C એ 1.1ને સંગત બિંદુ છે.

(d) 2.5
એ સ્પષ્ટ છે કે 2.5 એ 2 અને 3ની વચ્ચે છે.
હવે, સંખ્યારેખા ઉપર 2 અને 3ની વચ્ચે 10 સરખા ભાગ પાડો. સંખ્યારેખા ઉપર આમાંના પહેલા પાંચ ભાગ લો. બિંદુ D એ 2.5ને સંગત બિંદુ છે.

પ્રશ્ન 9.
આપેલ સંખ્યારેખા ઉપર બિંદુઓ A, B, C, D કઈ દશાંશ સંખ્યાનું નિરૂપણ કરે છે?
![]()
જવાબ:
(i) બિંદુ A
બિંદુ A એ 0 અને 1ની વચ્ચે છે. 0 અને 1ની વચ્ચે 10 સરખા ભાગ પાડેલા છે. એમાંના આઠમા ભાગ પર બિંદુ A છે.
∴ 0.8ને સંગત બિંદુ A છે.
![]()
(ii) બિંદુ B
બિંદુ B એ 1 અને 2ની વચ્ચે છે. 1 અને 2ની વચ્ચે 10 સરખા ભાગ પાડેલા છે. એમાંના ત્રીજા ભાગ પર બિંદુ B છે.
∴ 1.3ને સંગત બિંદુ B છે.
(iii) બિંદુ C
બિંદુ C એ 2 અને 3ની વચ્ચે છે. 2 અને 3ની વચ્ચે 10 સરખા ભાગ પાડેલા છે. એમાંના બીજા ભાગ પર બિંદુ C છે.
∴ 2.2ને સંગત બિંદુ C છે.
(iv) બિંદુ D
બિંદુ D એ 2 અને 3ની વચ્ચે છે. 2 અને 3ની વચ્ચે 10 સરખા ભાગ પાડેલા છે. એમાંના નવમા ભાગ પર બિંદુ D છે.
∴ 2.9ને સંગત બિંદુ D છે.
પ્રશ્ન 10.
(a) રમેશની નોટબુકની લંબાઈ 9 સેમી અને 5 મિમી છે. સેમીમાં તેની લંબાઈ કેટલી થશે?
(b) ચણાના નાના છોડની લંબાઈ 65 મિમી છે. તેની લંબાઈ સેમીમાં દર્શાવો.
જવાબ:
(a) 10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = \(\frac{1}{10}\) સેમી .
હવે, રમેશની નોટબુકની લંબાઈ = 9 સેમી 5 મિમી
= 9 સેમી + 5 × \(\frac{1}{10}\) સેમી
= 9 સેમી + \(\frac{5}{10}\) સેમી
= 9 સેમી + 0.5 સેમી
= (9 + 0.5) સેમી = 9.5 સેમી
રમેશની નોટબુકની લંબાઈ 9.5 સેમી છે.
![]()
(b) 10 મિમી = 1 સેમી થાય. ∴ 1 મિમી = \(\frac{1}{10}\) સેમી
હવે, ચણાના નાના છોડની લંબાઈ = 65 મિમી
= 65 × \(\frac{1}{10}\) સેમી
= \(\frac{65}{10}\) સેમી
= 6.5 સેમી
ચણાના નાના છોડની લંબાઈ 6.5 સેમી છે.