Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 8 Decimals InText Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 8 Decimals InText Questions
Try These (Page 165)
Question 1.
Does canyon now write the following as decimals?
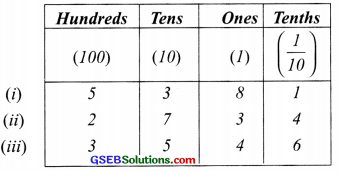
Solution:
We have,
(i) 5 hundreds + 3 tens + 8 ones + 1 tenth
= 5 × 100 + 3 × 10 + 8 × 1 + 1 × \(\frac { 1 }{ 10 }\)
= 500 + 30 + 8 + \(\frac { 1 }{ 10 }\)
= 500 + \(\frac { 1 }{ 10 }\) = 538.1
(ii) 2 hundreds + 7 tens + 3 ones + 4 tenths
= 2 × 100 + 7 × 10 + 3 × 1 + 4 × \(\frac { 1 }{ 10 }\)
= 200 + 70 + 3 + \(\frac { 4 }{ 10 }\)
= 273 + \(\frac { 4 }{ 10 }\) = 273.4
(iii) 3 hundreds + 5 tens + 4 ones + 6 tenths
= 3 × 100 + 5 × 10 + 4 × 1 + 6 × \(\frac { 1 }{ 10 }\)
= 300 + 50 + 4 + \(\frac { 6 }{ 10 }\)
= 354 + \(\frac { 6 }{ 10 }\) = 354.6
![]()
Question 2.
Write the lengths of Ravi s and Raju’s pencils in ‘cm ’ using decimals. When Ravi and Raju measured the lengths of their pencils. Ravi s pencil was 7 cm and 5 mm long and Raju s pencil was 8 cm 3 mm long.
Solution:
We know that:
10 mm = 1 cm
Therefore, 1 mm = \(\frac { 1 }{ 10 }\) cm
5 mm = 5 × \(\frac { 1 }{ 10 }\) cm = \(\frac { 5 }{ 10 }\) cm
and 3 mm = 3 × \(\frac { 1 }{ 10 }\) cm = \(\frac { 3 }{ 10 }\) cm
Now, 7 cm 5mm = 7 cm + 5 cm
= 7 cm + \(\frac { 5 }{ 10 }\) cm
= 7.5 cm
Thus, lengths of Ravi’s pencil = 7.5 cm
Again,
8 cm 3 mm = 8 cm + 3 mm
= 8 cm + \(\frac { 3 }{ 10 }\) cm
= 8.3 cm
Thus, length of Raju’s pencil = 8.3 cm
![]()
Question 3.
Make three more examples similar to the one given in question 1 and solve them.
Solution:
Please try yourself.
Try These (Page 167)
Question 1.
Write \(\frac { 3 }{ 2 }\) , \(\frac { 4 }{ 5 }\) , \(\frac { 8 }{ 5 }\) in decimal notation.
Solution:
(i) \(\frac { 3 }{ 2 }\)
We have, \(\frac { 3 }{ 2 }\) = \(\frac{3 \times 5}{2 \times 5}\) = \(\frac { 15 }{ 10 }\) = 1.5
∴ \(\frac { 3 }{ 2 }\) = 1.5
(ii) \(\frac { 4 }{ 5 }\)
We have, \(\frac { 4 }{ 5 }\) = \(\frac{4 \times 2}{5 \times 2}\) = \(\frac { 8 }{ 10 }\) = 0.8
= \(\frac { 8 }{ 10 }\) = 0.8
Thus, \(\frac { 4 }{ 5 }\) = 0.8
(iii) \(\frac { 8 }{ 5 }\)
We have, \(\frac { 8 }{ 5 }\) = \(\frac{8 \times 2}{5 \times 2}\) = \(\frac { 16 }{ 10 }\) = 1.6
Thus, \(\frac { 8 }{ 5 }\) = 1.6
Try These (Page 175)
Question 1.
(i) Write 2 rupees 5 paise and 2 rupees 50 paise in decimals.
(ii) Write 20 rupees 7 paise and 21 rupees 75 paise in decimals.
Solution:
(i) (a) 2 rupees 5 paise:
2 rupees + 5 paise = 2 rupees + \(\frac { 5 }{ 10 }\) rupees

= (2 + 0.05) rupees = ₹ 2.05
(b) 2 rupees 50 paise:
2 rupees + 50 paise = 2 rupees + \(\frac { 50 }{ 100 }\) rupees
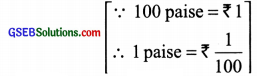
= (2 + 0.50) rupees = ₹ 2.50
(ii) (a) 20 rupees 7 paise:
20 rupees + 7 paise
= 20 rupees + 7 × \(\frac { 1 }{ 100 }\) rupess
![]()
= 20 rupees + 7 paise
= ₹ (20 + 0.07) = ₹ 20.07
(b) 21 rupees 75 paise:
21 rupees + 75 paise
= 21 rupees + 75 x \(\frac { 1 }{ 100 }\) rupees
= 21 rupees + \(\frac { 75 }{ 100 }\) rupees
= ₹ [21 + 0.75] = ₹ 21.75
Try These (page 176)
Question 1.
Can you write 4 mm in ‘cm’ using decimals?
Solution:
Yes,
Since 10 mm = 1 cm
∴ 1 mm = \(\frac { 1 }{ 10 }\) cm
or 4 mm = 4 × \(\frac { 1 }{ 10 }\) cm = 0.4 cm
![]()
Question 2.
How will you write 7 cm 5 mm in ‘cm’ using decimals?
Solution:
7 cm 5 mm:
Since, 10 mm = 1 cm
Now, 7 cm 5 mm = 7 cm + 5 mm
= 7 cm + 5 × \(\frac { 1 }{ 10 }\) cm = ![]() cm
cm
= (7 + 0.5) cm = 7.5 cm
![]()
Question 3.
Can you now write 52 m as ‘km’ using decimals? How will you write 340m as ‘km’ using decimals? how will you write 2008 m in ‘km’?
Solution:
Yes, we can change the given ‘meters’ into kilometers.
(a) 52 m
∵ 1000 m = 1 m
∴ 1 m = \(\frac { 1 }{ 1000 }\) km
or 52 m = 52 × \(\frac { 1 }{ 1000 }\) km = 0.052 km
(b) 340 m
∵ 1 m = \(\frac { 1 }{ 1000 }\) km
∴ 340 m = 340 × \(\frac { 1 }{ 1000 }\) km
= \(\frac { 340 }{ 1000 }\) km = 0.340 km
(c) 2008 m
∵ 1 m = \(\frac { 1 }{ 1000 }\) km
∴ 2008 m = 2008 × \(\frac { 1 }{ 1000 }\) km = \(\frac { 2008 }{ 1000 }\) km
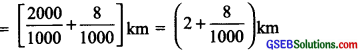
= (2 + 0.008) km = 2.008 km
Try These (page 176)
Question 1.
Can you now write 456 g as ‘kg’ using decimals?
Solution:
Since 1000 g = 1 kg
∴ 1 g = \(\frac { 1 }{ 1000 }\) kg
∴ 456 g = \(\frac { 1 }{ 1000 }\) x 456 kg
= \(\frac { 456 }{ 1000 }\) kg = 0.456 kg
![]()
Question 2.
How will you write 2 kg 9 g in ‘kg’ using decimals?
Solution:

Try These (page 178)
Question 1.
Find
(i) 0.29 + 0.36
(ii) 0.7 + 0.08
(iii) 1.54 + 1.80
(iv) 2.66 + 1.85
Solution:
(i) 0.29 + 0.36
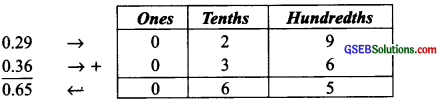
∵ (9 + 6) hundredths = 15 hundredths = 1 tenths + 5 hundredths
Thus, 0.29 + 0.36 = 0.65
(ii) 0.7 + 0.08
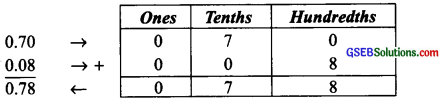
Thus, 0.7 + 0.08 = 0.78
(iii) 1.54 + 1.80
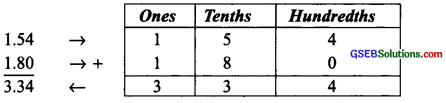
Thus, 1.54 + 1.80 = 3.34
Note: ∵ 5 tenths + 8 tenths = 13 tenths and 13 tenths = 10 tenths + 3 tenths = 1 one + 3 tenths
(iv) 2.66 + 1.85
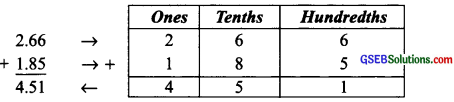
Thus, 2.66 + 1.85 = 4.51
Try These (page 180)
Question 1.
Subtract 1.85 from 5.46
Solution:
1.85 and 5.46 are ‘like decimals’.

Here, 1 is borrowed from ‘ones’ and given to tenths such that:
4 tenths + 10 tenths = 14 tenths
5 ones – 1 one = 4 ones
![]()
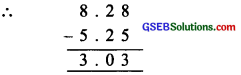
Question 2.
Subtract 5.25 from 8.28.
Solution:
5.25 and 8.28 are ‘like decimals’.
Question 3.
Subtract 0.95 from 2.29.
Solution:
0.95 and 2.29 are ‘like decimals’.

![]()
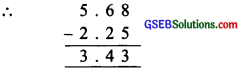
Question 4.
Subtract 2.25 from 5.68
Solution:
2.25 and 5.68 are ‘ like decimals’.