Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2
![]()
Question 1.
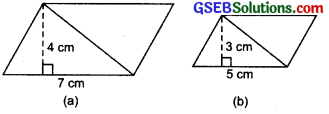
Find the area of each of the following parallelograms:
Solution:
(a) Here, Base (b) = 7 cm, Height (h) = 4 cm
∴ Area of the parallelogram
= b x h = 7 x 4 cm² = 28 cm²
(b) Here, Base =5 cm
Height (h) = 3 cm
∴ Area of the parallelogram = b x h
= 5 x 3 cm² = 15 cm²
(c) Here, Base(b) = 2.5 cm
Height (h) =3.5 cm
∴ Area of the parallelogram = b x h
= 2.5 x 3.5 cm²
= \(\frac { 25 }{ 10 }\) x \(\frac { 35 }{ 10 }\) cm²
= \(\frac { 875 }{ 100 }\)cm²
= 8.75 cm²
(d) Here, Base (b) =5 cm
Height (h) = 4.8 cm
∴ Area of the parallelogram = b x h
= 5 x 4.8 cm² = 24 cm²
(e) Here, Base (b) =2 cm
Height (h) = 4.4 cm
∴ Area of the parallelogram = b x h
= 2 x 4.4 cm² = 8.8 cm²
![]()
Question 2.
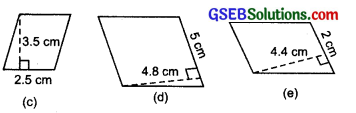
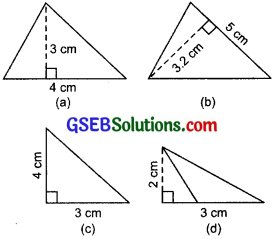
Find the area of each of the following triangles:
Solution:
(a) Here, Base (b) =4 cm
Height (h) = 3 cm
∴ Area of the triangle = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 4 x 3 cm² = 6 cm²
(b) Base (b) = 5 cm
Height (h) =3.2 cm
∴ Area of the triangle = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 5 x 3.2 cm²
(c) Here
Base (b) = 3 cm
Height (h) = 4 cm
∴ Area of the triangle = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 3 x 4 cm² = 6 cm²
(d) Here, Base (b) = 3 cm
Height (h) = 2 cm
∴ Area of the triangle = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 3 x 2cm²
= 3 cm²
Question 3.
Find the missing values:

Solution:
(a) Here,
Base (b) = 20 cm
Area = 246 cm²
Consider Height = h cm
∴ b x h = Area of the parallelogram
or 20 x h = 246 ⇒ h = \(\frac { 246 }{ 20 }\) cm
= \(\frac { 123 }{ 10 }\) cm = 12.3 cm
Thus, the missing value (height) = 12.3 cm
(b) Here, Height (h) = 15 cm
Area of the parallelogram = 154.5 cm²
Suppose the base of the parallelgoram = b cm
∴ b x h = 154.5 ⇒ b x 15 = 154.5
or b = \(\frac { 154.5 }{ 15 }\) = 10.3 cm
Thus, the missing value (base) = 10.3 cm
(c) Here, Height (h) = 8.4 cm
Area of the parallelogram = 48.72 cm²
Suppose the base of the parallelogram = b cm
∴ b x h = 48.72
b x 8.4 = 48.72
or b = \(\frac { 48.72 }{ 8.4 }\)
Thus, the missing value (base) = 5.8 cm
(d) Here, Base (b) = 15.6 cm
Area of the parallelogram = 16.38 cm²
Let the height be h cm.
∴ b x h = 6.38
or 15.6 x h = 16.38
or h = \(\frac { 16.38 }{ 15.6 }\) = 1.05 cm
Thus, the missing value (height) = 1.05 cm
![]()
Question 4.
Find the missing values:

Solution:
(i) Here, Base (b) = 15 cm
Area of the triangle = 87 cm² Let the height be h cm
∴ \(\frac { 1 }{ 2 }\) x b x h = 87
or \(\frac { 1 }{ 2 }\) x 15 x h = 87
or h = \(\frac { 87×2 }{ 15 }\)
= \(\frac { 174 }{ 15 }\) = 11.6 cm
∴ The missing value (height) = 11.6 cm
(ii) Here, Height (h) =31.4 mm
Area of the triangle = 1256 mm²
Let the base be b mm
∴\(\frac { 1 }{ 2 }\) x b x h = 1256
or \(\frac { 1 }{ 2 }\) x b x 31.4 = 1256
or b = \(\frac { 1256×2 }{ 31.4 }\)
= \(\frac { 2512 }{ 31.4 }\) = 80 mm
Thus, the missing value (base) = 80 mm.
(iii) Here, Base (b) = 22 cm
Area of the triangle = 170.5 cm²
Let the height be h cm
∴ \(\frac { 1 }{ 2 }\) x b x h = 170.5
or \(\frac { 1 }{ 2 }\) x 22 x h = 170.5
∴ h = \(\frac { 170.5×2 }{ 22 }\)
= \(\frac { 170.5 }{ 11 }\) = 15.5 mm
∴The missing value (height) = 15.5 cm.
Question 5.
PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm.
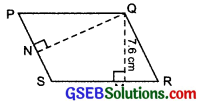
Find:
(a) the area of the parallelogram PQRS.
(b) QN, if PS = 8 cm.
Solution:
Here, Base (SR) = 12 cm
Corresponding height (QM) = 7.6 cm
(a) ∴ Area of the parallelogram PQRS = b x h
= SR x QM
= 12 x 7.6 cm²
= 91.2 cm²
(b) Now, Area of the parallelogram = 91.2 cm²
Base (PS) = 8 cm
Let the corresponding height (QN) be h cm
∴ b x h = 91.2
or 8 x h = 91.2
or h = \(\frac { 91.2 }{ 8 }\)
∴ QN = 11.4 cm
![]()
Question 6.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470 cm², AB = 35 cm and AD = 49 cm, find the length of BM and DL.
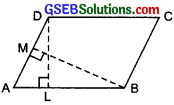
Solution:
Since, Area of the parallelogram ABCD = Base x height
= AD x BM
∴ AD x BM = 1470
[∵ Area = 1470 cm²]
or 49 x BM = 1470
or BM = \(\frac { 1470 }{ 49 }\) = 30 cm
Again, Area of parallelogram ABCD = Base x Height = AB x DL
∴ AB X DL = 1470
or 35 x DL = 1470
or DL = \(\frac { 1470 }{ 49 }\) cm = 42 cm
Question 7.
∆ABC is right angled at A. AD is perpendicular to BC. If AB = 5 cm, BC =13 cm and AC = 12 cm, find the area of ∆ABC. Also find the length of AD.
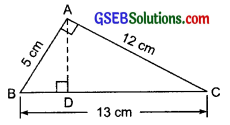
Solution:

Question 8.
∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB, i.e. CE?
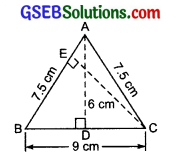
Solution:
Here, base, BC = 9 cm
Corresponding height, AD = 6 cm

Thus, height CE = 7.2 cm
![]()