Gujarat Board GSEB Solutions Class 7 Maths Chapter 14 સંમિતિ Ex 14.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 14 સંમિતિ Ex 14.3
પ્રશ્ન 1.
કોઈ બે એવા અંક જણાવો કે જેની રેખિક સંમિતિ અને પરિભ્રમણ સમિતિ બને હોય.
જવાબઃ
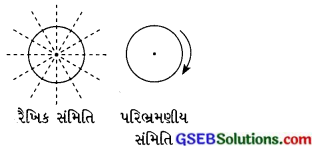
આપણે અંક શૂન્યની રેખિક સમિતિ તપાસીએ. શૂન્ય એ વર્તુળાકાર છે, તેથી અસંખ્ય રેખિક સંમિતિની કક્ષા ધરાવે છે. તેવી જ રીતે શૂન્યની પરિભ્રમણીય સમિતિની કક્ષા પણ અસંખ્ય છે.
હવે, આપણે અંક આઠ (8)ની રેખિક સંમિતિ તપાસીએ.
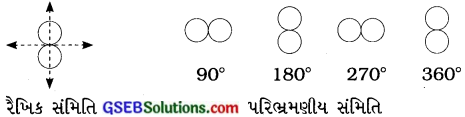
અંક આઠ (8) રેખિક સંમિતિની કક્ષા ધરાવે છે. તેવી જ રીતે શૂન્યની પરિભ્રમણીય સમિતિની કક્ષા પણ અસંખ્ય છે. સંમિતિની પણ બે કક્ષા ધરાવે છે.
![]()
2. નીચેના દરેકમાં શક્ય હોય, તો કાચી આકૃતિ દોરોઃ
પ્રશ્ન (i)
એકથી વધુ ક્રમની રેખિક અને પરિભ્રમણીય બંને સંમિતિ હોય તેવો ત્રિકોણ.
જવાબ:
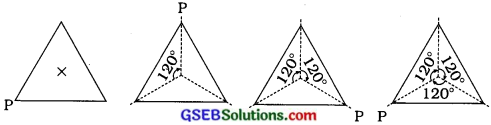
સમબાજુ ત્રિકોણને એકથી વધુ ક્રમની રેખિક સંમિતિ છે

અહીં આકૃતિમાં જુઓ. સમબાજુ ત્રિકોણને એકથી વધુ ક્રમની પરિભ્રમણીય સંમિતિ છે. (3 છે.)
પ્રશ્ન (ii)
એકમાત્ર રેખિક સમિતિ હોય પણ પરિભ્રમણીય સંમિતિ ન હોય તેવો ત્રિકોણ.
જવાબ:
એકમાત્ર રેખિક સંમિતિ હોય પણ પરિભ્રમણીય સંમિતિ ન હોય તેવો સમદ્વિબાજુ ત્રિકોણ છે.

![]()
પ્રશ્ન (iii)
એકથી વધુ ક્રમની પરિભ્રમણીય સમિતિ હોય પણ રૈખિક સંમિતિ ન હોય તેવો ચતુષ્કોણ.
જવાબ:
એકથી વધુ ક્રમની પરિભ્રમણીય સંમિતિ હોય પણ રેખિક સંમિતિ ન હોય તેવો સમાંતરબાજુ ચતુષ્કોણ છે.

પ્રશ્ન (iv)
એકમાત્ર રેખિક સમિતિ હોય પણ પરિભ્રમણીય સંમિતિ ન હોય તેવો ચતુષ્કોણ.
જવાબ:
એકમાત્ર રેખિક સંમિતિ હોય પણ પરિભ્રમણીય સંમિતિ ન હોય તેવો ચતુષ્કોણ સમદ્વિબાજુ સમલંબ ચતુષ્કોણ છે.

પ્રશ્ન 3.
જો કોઈ આકૃતિમાં બે અથવા વધુ રૈખિક સંમિતિ છે, તો શું પરિભ્રમણીય સંમિતિનો ક્રમ 1 કરતાં વધુ છે?
જવાબઃ
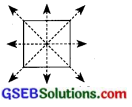
હા, આ આકૃતિમાં બે અથવા વધુ રેખિક સંમિતિ છે, તો કે આ પરિભ્રમણીય સંમિતિનો ક્રમ 1 કરતાં વધુ હોય જ. જઓ ચોરસને રેખિક સમિતિ 4 છે અને પરિભ્રમણીય સંમિતિ જે.
![]()
પ્રશ્ન 4.
ખાલી જગ્યા પૂરોઃ
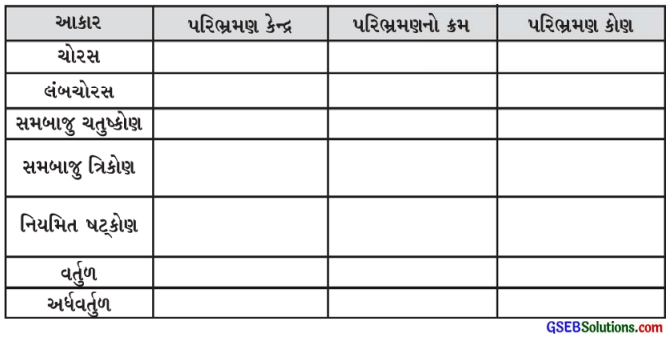
જવાબઃ
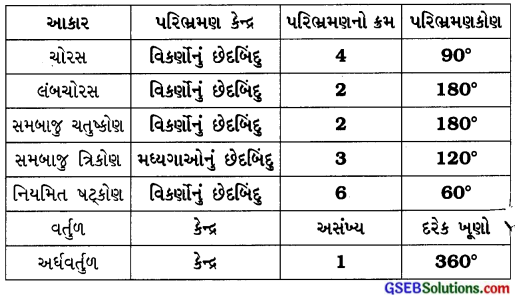
પ્રશ્ન 5.
એવા ચતુષ્કોણનું નામ જણાવો કે જેની રૈખિક સંમિતિ અને પરિભ્રમણ સમિતિ બંનેનો ક્રમ 1 કરતાં વધુ હોય.
જવાબઃ
ચોરસ, લંબચોરસ અને સમબાજુ ચતુષ્કોણ એ એવા ચતુષ્કોણ છે કે જેમને રેખિક સમિતિ અને પરિભ્રમણ સંમિતિ બંનેના ક્રમ 1 કરતાં વધુ છે.
![]()
પ્રશ્ન 6.
કેન્દ્રથી 60° ફર્યા પછી આકૃતિ તેની મૂળ સ્થિતિના જેવી જ દેખાય છે. બીજા કયા ખૂણાઓ માટે આવું થશે?
જવાબઃ
આકૃતિને કેન્દ્રથી 60°ના ખૂણે ફેરવતાં આકૃતિ મૂળ સ્થિતિના જેવી જ જો દેખાય તો આ જ આકૃતિ 120°, 180°, 240°, 300° અને 360° ખૂણે મૂળ સ્થિતિ જેવી જ દેખાશે.
7. નીચે આપેલા ખૂણાઓ માટે શું આપણે 1 કરતાં વધુ ક્રમની પરિભ્રમણીય સંમિતિ મેળવી શકીએ?
પ્રશ્ન (i)
45°
જવાબ:
360°ને 45 વડે નિઃશેષ ભાગી શકાય છે.
∴ 45°ના ખૂણા માટે 1 કરતાં વધુ ક્રમની પરિભ્રમણીય સંમિતિ મેળવી શકાય.
![]()
પ્રશ્ન (ii)
17°
જવાબ:
360°ને 17° વડે નિઃશેષ ભાગી શકાય નહીં.
∴ 17°ના ખૂણા માટે 1 કરતાં વધુ ક્રમની પરિભ્રમણીય સંમિતિ મેળવી ન શકાય.