Gujarat Board GSEB Solutions Class 7 Maths Chapter 5 રેખા અને ખૂણા InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 5 રેખા અને ખૂણા InText Questions
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 94)
તમારી આસપાસની 10 આકૃતિઓના ખૂણાની યાદી બનાવો અને તેમાંથી લઘુકોણ, ગુરુકોણ અને કાટકોણને ઓળખો.
ઉત્તરઃ
(1) ટેબલની ઉપરની સપાટીની બે કિનાર વચ્ચેનો ખૂણો – કાટકોણ
(2) કંપાસબૉક્સની લંબાઈ-પહોળાઈ વચ્ચેનો ખૂણો – કાટકોણ
(3) કાટખૂણિયાની બે ધાર વચ્ચેનો ખૂણો – કાટકોણ તથા લઘુકોણો
(4) કાતરનાં બે પાંખિયાં વચ્ચેનો ખૂણો – લઘુકોણ
(5) પુસ્તકની લંબાઈ-પહોળાઈ વચ્ચેનો ખૂણો – કાટકોણ
(6) કાજુકતરીના ખૂણા-લઘુકોણ તથા ગુરુકોણ
(7) માપપટ્ટીની પાસપાસેની બે ધાર વચ્ચેનો ખૂણો – કાટકોણ
(8) ઘરની પાસપાસેની બે દીવાલો વચ્ચેનો ખૂણો – કાટકોણ
(9) નોટબુકની પાસપાસેની બે ધારો વચ્ચેનો ખૂણો – કાટકોણ
(10) ઘરના બારણાની લંબાઈ-પહોળાઈ વચ્ચેનો ખૂણો – કાટકોણ
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 95)
1. શું બે લઘુકોણો પરસ્પર કોટિકોણ હોઈ શકે?
ઉત્તરઃ
હા, બે લઘુકોણો એ પરસ્પર કોટિકોણ હોઈ શકે.
દા. ત., 20°નો ખૂણો લઘુકોણ છે. 70°નો ખૂણો લઘુકોણ છે.
હવે, 20° + 70° = 90°
∴ 20° નો ખૂણો અને 70નો ખૂણો પરસ્પર કોટિકોણ છે.
2. શું બે ગુરુકોણો પરસ્પર કોટિકોણ હોઈ શકે?
ઉત્તરઃ
ના, બે ગુરુકોણો એ પરસ્પર કોટિકોણ ન હોઈ શકે.
કારણઃ પ્રત્યેક ગુરુકોણનું માપ 90°થી વધારે હોય. તેથી, બે ગુરુકોણનાં માપનો સરવાળો કદાપિ 90° ન હોઈ શકે.
3. શું છે કાટકોણો પરસ્પર કોટિકોણ હોઈ શકે?
ઉત્તરઃ
ના, બે કાટકોણો પરસ્પર કોટિકોણ ન હોઈ શકે.
કારણઃ એક કાટકોણનું માપ = 90°
બે કોટિકોણોનાં માપનો સરવાળો 90° થવો જોઈએ. તેથી, બે કાટકોણનાં માપનો સરવાળો 180° થઈ જાય પણ 90° ન થાય.
![]()
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 95)
1. નીચેનામાંથી કઈ જોડ કોટિકોણની છે?
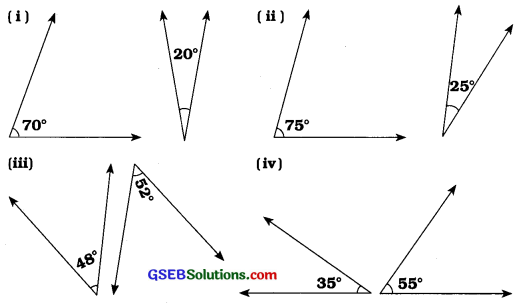
ઉત્તરઃ
(i) જુઓઃ 70° + 20° = 90°
∴ 70° અને 20નાં માપના ખૂણા કોટિકોણની જોડ છે.
(ii) જુઓઃ 75° + 25° = 100° અને 100° ≠ 90°
∴ 75° અને 25°નાં માપના ખૂણા કોટિકોણની જોડ નથી.
(ii) જુઓઃ 48 + 529 = 100° અને 100° ≠ 90°
∴ 48° અને 52°નાં માપના ખૂણા કોટિકોણની જોડ નથી.
(iv) જુઓઃ 35° + 55° = 90°
∴ 35° અને 55°નાં માપના ખૂણા કોટિકોણની જોડ છે.
2. નીચેના દરેક ખૂણાના કોટિકોણનાં માપ શું છે?
(i) 45° (ii) 65° (iii) 41° (iv) 54°
ઉત્તરઃ
(i) 45°ના માપના ખૂણાના કોટિકોણનું માપ = 90° – 45° = 45°
(ii) 65°ના માપના ખૂણાના કોટિકોણનું માપ = 90° – 65° = 25°
(iii) 41°ના માપના ખૂણાના કોટિકોણનું માપ = 90° – 41° = 49°
(iv) 54°ના માપના ખૂણાના કોટિકોણનું માપ = 90° – 54° = 36°
3. બે કોટિકોણનાં માપ વચ્ચેનો તફાવત 12° છે. તેમનાં માપ શોધો.
ઉત્તરઃ
ધારો કે બે કોટિકોણમાંથી એક ખૂણાનું માપ x છે.
બે ખૂણાઓનાં માપનો તફાવત 12° છે.
∴ બીજા ખૂણાનું માપ = 2x + 12°
હવે, બે કોટિકોણનાં માપનો સરવાળો 90° થાય.
∴ x + (x + 12°) = 90°
∴ 2x + 12° = 90°
∴ 2x = 90° – 12° (12°ને જમણી બાજુ લઈ જતાં)
∴ 2x = 78°
∴ \(\frac{2 x}{2}=\frac{78^{\circ}}{2}\) (બંને બાજુ 2 વડે ભાગતાં)
∴ x = 39°
અને બીજા ખૂણાનું માપ = x + 12° = 39° + 12° = 51°
આ બે કોટિકોણનાં માપ 39° અને 51° છે.
![]()
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 96)
1. શું બે ગુરુકોણો પૂરકકોણ બની શકે?
ઉત્તરઃ
ના, બે ગુરુકોણો એકબીજાના પૂરકકોણ ન બની શકે.
કારણઃ ગુરુકોણનું માપ 90થી વધારે હોય. તેથી, બે ગુરુકોણનાં માપનો સરવાળો 180°થી વધી જાય.
2. શું બે લઘુકોણો પૂરકકોણ બની શકે?
ઉત્તરઃ
ના, બે લઘુકોણો એકબીજાના પૂરકકોણ ન બની શકે.
કારણઃ લઘુકોણનું માપ 90° કરતાં ઓછું હોય. તેથી, બે લઘુકોણનાં માપનો સરવાળો 180°થી ઓછો થાય.
3. શું બે કાટખૂણાઓ પૂરકકોણ બની શકે?
ઉત્તરઃ
હા, બે કાટખૂણાઓ એકબીજાના પૂરકકોણ બની શકે છે.
કારણઃ કાટખૂણાનું માપ 90° હોય. તેથી, બે કાટખૂણાનાં માપનો સરવાળો 180° થાય.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 96-97)
1. નીચે આપેલા ખૂણાઓમાંથી પૂરકકોણની જોડ શોધોઃ
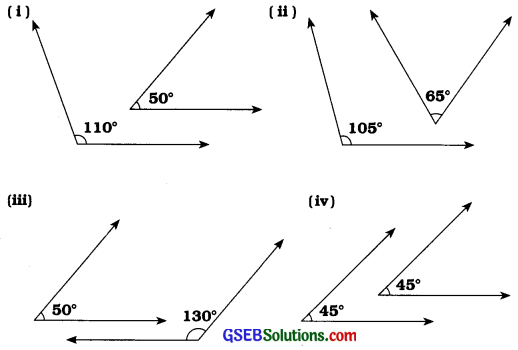
ઉત્તરઃ
(i) જુઓ : 110° + 50° = 160° અને 160° ≠ 180°
∴ 110° અને 50°નાં માપના ખૂણા પૂરકકોણની જોડ નથી.
(ii) જુઓ : 105° + 65° = 170° અને 170° ≠ 180°
∴ 105 અને 65નાં માપના ખૂણા પૂરકકોણની જોડ નથી.
(iii) જુઓ : 50° + 130° = 180°
∴ 50° અને 130નાં માપના ખૂણા પૂરકકોણની જોડ છે.
(iv) જુઓઃ 45°+ 45° = 90° અને 90° ≠ 180°
∴ 45° અને 45નાં માપના ખૂણા પૂરકકોણની જોડ નથી.
![]()
2. નીચેના દરેક ખૂણાના પૂરકકોણનું માપ શું થશે?
(i) 100° (ii) 90° (iii) 55° (iv) 125°
ઉત્તરઃ
(i) 100°ના માપના ખૂણાના પૂરકકોણનું માપ = 180° – 100° = 80°
(ii) 90°ના માપના ખૂણાના પૂરકકોણનું માપ = 180° – 90° = 90°
(ii) 55°ના માપના ખૂણાના પૂરકકોણનું માપ = 180° – 55° = 125°
(iv) 125°ના માપના ખૂણાના પૂરકકોણનું માપ = 180° – 125° = 55°
3. બે પૂરકકોણમાંના મોટા ખૂણાનું માપ નાના ખૂણાના માપ કરતાં 44° વધારે છે, તો તેમનાં માપ શોધો.
ઉત્તરઃ
ધારો કે બે પૂરકકોણોમાંથી નાના માપના ખૂણાનું માપ x છે.
∴ મોટા માપવાળા ખૂણાનું માપ = (x + 44°)
હવે, બે પૂરકોણોનાં માપનો સરવાળો 180° થાય.
∴ x + (x + 44°) = 180°
∴ 2x + 44° = 180°
∴ 2x = 180° – 44° (44°ને જમણી બાજુ લઈ જતાં)
∴ 2x = 136°
\(\frac{2 x}{2}=\frac{136^{\circ}}{2}\) (બંને બાજુ 2 વડે ભાગતાં)
∴ x = 68°
∴ નાના ખૂણાનું માપ 68° છે. મોટા ખૂણાનું માપ = 68° + 44° = 112°
આમ, બંને પૂરકકોણોનાં માપ 68° અને 112° છે.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 97-98)
1. 1 અને 2 વડે દર્શાવેલા ખૂણાઓ આસનકોણ છે? જો નથી, તો શા માટે નથી?
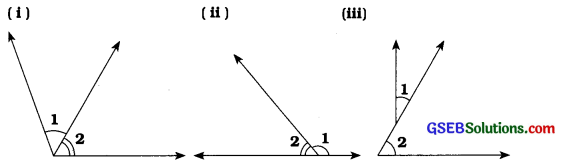
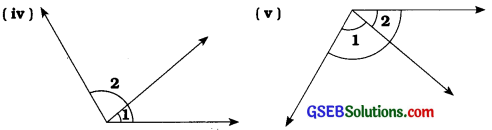
ઉત્તરઃ
(i) હા, ∠1 અને ∠2 એ આસન્નકોણ છે.
(ii) હા, ∠1 અને ∠2 એ આસન્નકોણ છે.
(iii) ના, ∠1 અને ∠2 એ આસન્નકોણ નથી.
કારણઃ ∠1 અને ∠2ને સામાન્ય શિરોબિંદુ નથી.
(iv) ના, ∠1 અને ∠2 એ આસન્નકોણ નથી.
કારણઃ ∠1 અને ∠2 અલગ ખૂણા નથી. ∠1 એ ∠2નો જ ભાગ છે.
(v) હા, ∠1 અને ∠2 એ આસન્નકોણ છે.
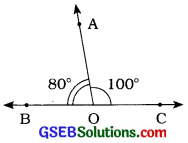
2. આપેલી આકૃતિમાં નીચેના ખૂણાઓ આસન્નકોણ છે?
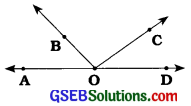
(a) ∠AOB અને ∠BOC
(b) ∠BOD અને ∠BOC
તમારો જવાબ ચકાસો.
ઉત્તરઃ
(a) હા, ∠AOB અને ∠BOC એ આસન્નકોણ છે.
કારણ: ∠AOB અને ∠BOCનું સામાન્ય શિરોબિંદુ O છે. વળી, તેમના ભુજ \(\overrightarrow{\mathrm{OA}}\) તથા \(\overrightarrow{\mathrm{OC}}\) એ સામાન્ય ભુજ \(\overrightarrow{\mathrm{OB}}\) ની બંને બાજુએ છે.
(b) ના, ∠BOD અને ∠BOC એ આસન્નકોણ નથી.
કારણ: ∠BOC એ ∠BODનો જ ભાગ છે. બંને અલગ ખૂણા નથી.
![]()
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 98)
1. બે આસનકોણ પૂરકકોણ હોઈ શકે?
ઉત્તરઃ
હા, બે આસન્નકોણ એ પૂરકકોણ હોઈ શકે.
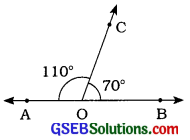
કારણઃ અહીં, આકૃતિમાં ∠AOC અને ∠BOC એ આસન્નકોણ છે. વળી, ∠AOC + ∠BOC = 180°. તેથી, ∠AOC અને ∠BOC એ પૂરકકોણ પણ છે.
2. બે આસન્નકોણ કોટિકોણ હોઈ શકે?
ઉત્તરઃ
હા, બે આસન્નકોણ એ કોટિકોણ હોઈ શકે.
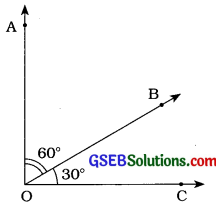
કારણ: અહીં, આકૃતિમાં ∠AOB અને ∠BOC એ આસન્નકોણ છે. વળી, ∠AOB + ∠BOC = 90°. તેથી, ∠AOB અને ∠BOC કોટિકોણ પણ છે.
3. બે ગુરુકોણ આસન કોણ હોઈ શકે?
ઉત્તરઃ
હા, બે ગુરુકોણ એ આસન્નકોણ હોઈ શકે.
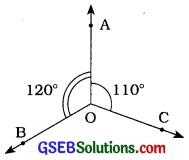
કારણ: અહીં, આકૃતિમાં ∠AOB અને ∠AOC એ ગુરુકોણ છે. વળી, ∠AOB અને ∠AOC એ આસન્નકોણ પણ છે.
4. એક લઘુકોણ અને બીજો ગુરુકોણ આસનકોણ હોઈ શકે?
ઉત્તરઃ
હા, એક લઘુકોણ અને બીજો ગુરુકોણ આસન્નકોણ હોઈ શકે.
કારણઃ અહીં, આકૃતિમાં ∠AOB અને ∠AOC એ આસન્નકોણ છે. વળી, ∠AOB એ લઘુકોણ છે. જ્યારે ∠AOC એ ગુરુકોણ છે.
![]()
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 99)
1. શું બે લઘુકોણ રૈખિક જોડ રચી શકે?
ઉત્તરઃ
ના, બે લઘુકોણ એ રેખિક ખૂણાની જોડ ન રચી શકે.
કારણઃ બે લઘુકોણનાં માપનો સરવાળો 180થી ઓછો થાય, કારણ કે દરેક લઘુકોણનું માપ 90° કરતાં ઓછું હોય. રેખિક જોડના ખૂણાઓનાં માપનો સરવાળો 180° થવો જોઈએ.
2. શું બે ગુરુકોણ રખિક જોડ રચી શકે?
ઉત્તરઃ
ના, બે ગુરુકોણ એ રેખિક ખૂણાની જોડ ન રચી શકે.
કારણઃ બે ગુરુકોણનાં માપનો સરવાળો 180° થી વધી જાય, કારણ કે દરેક ગુરુકોણનું માપ 90°થી વધારે હોય. રેખિક જોડના ખૂણાઓનાં માપનો સરવાળો 180° જ થવો જોઈએ.
3. શું બે કાટકોણ રૈખિક જોડ રચી શકે?
ઉત્તરઃ
હા, બે કાટકોણ એ રેખિક ખૂણાની જોડ રચે.
કારણઃ બે કાટકોણનાં માપનો સરવાળો 180° થાય છે, કારણ કે દરેક કાટકોણનું માપ 90° હોય છે. રેખિક જોડના ખૂણાઓનાં માપનો સરવાળો 180° થવો જોઈએ.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 99)
નીચે આપેલી ખૂણાઓની જોડ પૈકી કઈ જોડ સેખિક જોડ રચે છે?
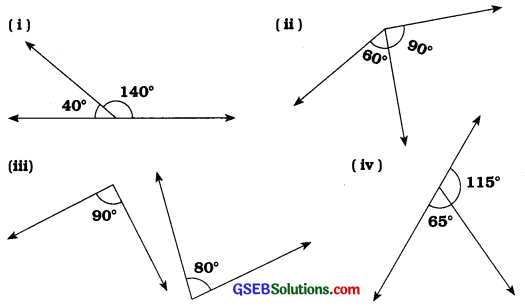
ઉત્તરઃ
(i) અહીં, આપેલા બંને ખૂણા રેખિક ખૂણાઓની જોડ રચે છે.
જુઓઃ 140° + 40° = 180°
કારણ: અહીં, બને ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
(ii) અહીં, આપેલા બંને ખૂણા રેખિક ખૂણાઓની જોડ રચતા નથી.
જુઓઃ 60° + 90° = 150° અને 150° ≠ 180°
કારણઃ અહીં, બંને ખૂણાઓનાં માપનો સરવાળો 180° થતો નથી. 180°થી ઓછો છે.
(iii) અહીં, આપેલા બંને ખૂણા રેખિક ખૂણાઓની જોડ રચતા નથી.
જુઓઃ 90° + 80° = 170° અને 170° ≠ 180°
કારણઃ અહીં, બંને ખૂણાઓનાં માપનો સરવાળો 180° થતો નથી. 180°થી ઓછો છે.
(iv) અહીં, આપેલા બંને ખૂણા રૈખિક ખૂણાઓની જોડ રચે છે.
જુઓઃ 115°+ 65° = 180°
કારણઃ અહીં, બંને ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
![]()
પ્રયત્ન કરોઃ (પાઠ્યપુસ્તક પાન નંબર 101)
1. અહીં આપેલી આકૃતિમાં જો ∠1 = 30, તો ∠2 અને ∠3 મેળવો.
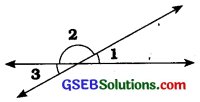
ઉત્તરઃ
જુઓ અહીં, ∠3 અને ∠1 એ અભિકોણો છે.
∴ ∠3 = ∠1
પણ, ∠1 = 30° ∴ ∠3 = 30° … (i)
કે હવે, ∠3 અને ∠2 એ રેખિક જોડના ખૂણા છે.
∴ ∠3 + ∠2 = 180°
∴ 30° + ∠2 = 180°
∴ ∠2 = 180° – 30° = 150° … (i)
આમ, ∠2 = 150° અને ∠3 = 30°
2. તમારી આસપાસમાંથી અભિકોણોનું ઉદાહરણ આપો.
ઉત્તરઃ
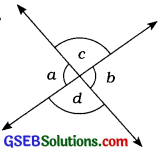
નોટબુકમાં એકબીજીને છેદતી બે રેખાઓ દોરો. આથી બનતા સામસામેના ખૂણા એ અભિકોણો છે. અહીં, a અને b ખૂણાઓ તથા c અને d ખૂણાઓ અભિકોણો છે.
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 104)
1. અહીં આકૃતિમાં AC અને BE, બિંદુ Pમાં છેદે છે. AC અને BC, બિંદુ માં છેદે છે. AC અને EC, બિંદુ Cમાં છેદે છે. છેદતા રેખાખંડોની બીજી દસ જોડ શોધવાનો પ્રયત્ન કરો:
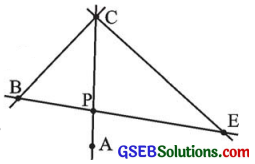
ઉત્તરઃ
છેદતા રેખાખંડોની બીજી કોડ નીચે પ્રમાણે છે :
(i) BC અને BE, BP અને BC જે બિંદુ Bમાં છેદે છે.
(ii) CB અને CE, CP અને CB, CP અને CE જે બિંદુ Cમાં છેદે છે.
(iii) EB અને EC, EP અને EC જે બિંદુ Eમાં છેદે છે.
(iv) PB અને PC, PE અને PC જે બિંદુ Pમાં છેદે છે.
(v) PA અને PB, PA અને PE જે બિંદુ Pમાં છેદે છે.
2. શું બે રેખાઓ કે બે રેખાખંડો છેદતા હોય એ જરૂરી છે?
ઉત્તરઃ
ના, બે રેખાઓ કે બે રેખાખંડો એકબીજાને છેદે અથવા ન પણ છે.
3. બે રેખા એક કરતાં વધુ બિંદુમાં છેદી શકે? વિચારો.
ઉત્તરઃ
ના, બે રેખાઓ છેદે તો એક અને માત્ર એક જ બિંદુમાં છેદી શકે, એક કરતાં વધારે બિંદુમાં ન છેદી શકે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 104)
1. કાટખૂણે છેદતી રેખાઓનાં ઉદાહરણો તમારી આસપાસમાં શોધો.
ઉત્તરઃ
(i) ઓરડાની બે પાસપાસેની દીવાલો વચ્ચેનો ખૂણો
(ii) કંપાસપેટીની લંબાઈ-પહોળાઈ વચ્ચેનો ખૂણો
(iii) નોટબુકની કિનારો વચ્ચેનો ખૂણો
(iv) પુસ્તકની કિનારો વચ્ચેનો ખૂણો
2. સમબાજુ ત્રિકોણનાં શિરોબિંદુઓ આગળ છેદતી રેખાઓથી બનતા ખૂણાનાં માપ મેળવો.
ઉત્તરઃ
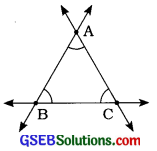
અહીં, રેખાઓ પરસ્પર છેદવાથી શિરોબિંદુ A, B, C બને છે.
અહીં, આ ત્રિકોણ સમબાજુ ત્રિકોણ છે.
તેની ત્રણે બાજુઓનાં માપ સરખાં છે. તેથી ત્રણે ખૂણાઓનાં માપ સરખાં છે.
આમ, ∠Aનું માપ = 60°, ∠Bનું માપ = 60° અને ∠Cનું માપ = 60°
3. કોઈ પણ લંબચોરસ દોરો અને તેનાં શિરોબિંદુઓ આગળ છેદતી રેખાઓથી બનતા ખૂણાઓનાં માપ મેળવો.
ઉત્તરઃ
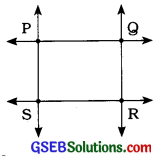
☐PQRS એ લંબચોરસ છે. લંબચોરસના બધા ખૂણા કાટખૂણા હોય.
∠Pનું માપ = 90°, ∠Qનું માપ = 90°,
∠Rનું માપ = 90° અને ∠Sનું માપ = 90°
4. જો બે રેખાઓ છે, તો શું તે હંમેશાં કાટખૂણે જ છે?
ઉત્તરઃ
ના, બે રેખાઓ છે, તો તે હંમેશાં કાટખૂણે જ છે એવું નથી.
બે રેખાઓ ગમે તે માપના ખૂણે છે. નીચે જુઓ:
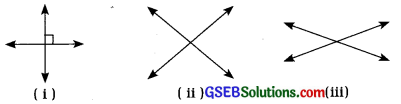
આકૃતિ (i)માં બે રેખાઓ કાટખૂણે છેદે છે, જ્યારે (ii) અને (iii)માં રેખાઓ કાટખૂણે છેદતી નથી.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 105)
1. ધારો કે બે રેખાઓ આપી છે. આ રેખાઓ માટે તમે કેટલી છેદિકાઓ દોરી શકો?
ઉત્તરઃ
આપેલી બે રેખાઓને છેદતી અસંખ્ય છેદિકાઓ દોરી શકાય. \(\overleftrightarrow{\mathrm{AB}}\) અને \(\overleftrightarrow{\mathrm{CD}}\) ને અસંખ્ય છેદિકાઓ દોરી શકાય.
2. જો એક રેખા ત્રણ રેખાઓની છેદિકા હોય, તો કેટલાં છેદબિંદુઓ હોય?
ઉત્તરઃ
આકૃતિમાં બતાવ્યા પ્રમાણે ત્રણ જુદાં જુદાં છેદબિંદુ મળે. જુઓ \(\overleftrightarrow{\mathrm{AB}}\), \(\overleftrightarrow{\mathrm{CD}}\) અને \(\overleftrightarrow{\mathrm{EF}}\)ની છેદિકા lછે. જેથી ત્રણ છેદબિંદુઓ P, Q અને R મળે છે.
3. તમારી આસપાસમાંથી કેટલીક છેદિકાઓ શોધવાનો પ્રયત્ન કરો.
ઉત્તરઃ
(i) ટોવેલ ઍન્ડ (ii) રોડ ક્રૉસિંગ (iii) રેલવે લાઇન ક્રૉસિંગ (iv) બારીની ગ્રીલ

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર 106)
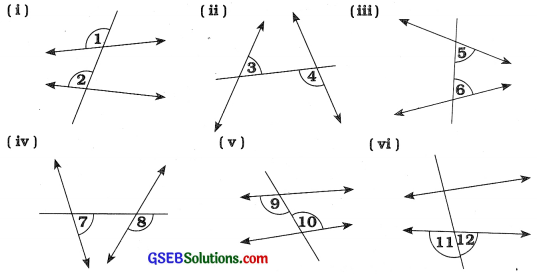
દરેક આકૃતિમાં ખૂણાની જોડને નામ આપોઃ
ઉત્તરઃ
(1) ∠1 અને ∠2 એ અનુકોણની જોડ છે.
(ii) ∠3 અને ∠4 એ અંતઃ યુગ્મકોણની જોડ છે.
(iii) ∠5 અને ∠6 એ છેદિકાની એક જ બાજુના અંતઃકોણની જોડ છે.
(iv) ∠7 અને ∠8 એ અનુકોણની જોડ છે.
(v) ∠9 અને ∠10 એ અંતઃ યુગ્મકોણની જોડ છે.
(vi) ∠11 અને ∠12 એ રખિક ખૂણાઓની જોડ છે.
![]()
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 109)
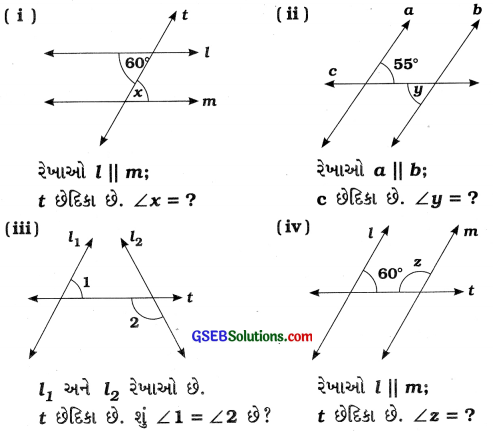
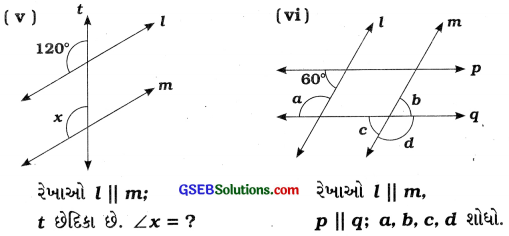
ઉત્તરઃ
(i) ∠x = 60°
કારણ : l || mને છેદિકા લે છેદવાથી ∠x અને 60° અંતઃ યુગ્મકોણ બને છે.
અંતઃ યુગ્મકોણનાં માપ સમાન હોય.
(ii) ∠y = 55°
કારણ : a || bને છેદિકા c છેદવાથી ∠y અને 55° અંતઃ યુગ્મકોણ બને છે.
અંતઃ યુગ્મકોણનાં માપ સમાન હોય.
(iii) ∠1 = ∠2 નથી.
કારણ: l1અને l2 સમાંતર રેખાઓ નથી. ∠1 અને ∠2 અંતઃ યુગ્મકોણ છે, પણ તે સમાન નથી.
(iv) ∠z = 120°
કારણ: l || mને છેદિકા છેદવાથી 60° અને z એ છેદિકાની એક જ બાજુના અંતઃકોણ બને છે.
∴ 60° + ∠z = 180° ∴ ∠z = 180° – 60°
∴ ∠z = 120°
(v) ∠x = 120°
કારણઃ l || mને છેદિકા માં છેદવાથી 120° અને x એ અનુકોણ બને છે. અનુકોણનાં માપ સમાન હોય.
(vi) (a) p || qને છેદિકા એ છેદવાથી 60° અને વ્ર છેદિકાની એક જ બાજુના અંતઃકોણ બને છે.
∴ 60° + ∠a = 180° ∴ ∠a = 180° – 60° ∴ ∠a = 120°
(b) l || mને છેદિકા q છેદવાથી વ અને d બાહ્ય યુગ્મકોણ બને છે. બાહ્ય યુગ્મકોણોનાં માપ સમાન હોય.
∴ ∠a = ∠d ∴ ∠d = 120°
(c) q અને m પરસ્પર છેદે છે. તેથી છે અને તે રેખિક જોડના ખૂણા બને છે.
∴ ∠b + ∠d = 180° ∴ ∠b + 120 = 180°
∴ ∠b = 180° – 120° ∴ ∠b = 60°
(d) q અને m પરસ્પર છેદે છે. તેથી ∠b અને ∠c અભિકોણો છે.
∴ ∠b = ∠c
∴ ∠b = 60° ∴ ∠c = 60°
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 110)
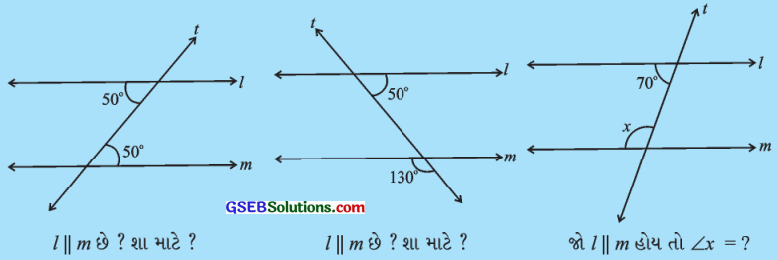
ઉત્તરઃ
(i) બે રેખાઓને એક છેદિકા છેદે, અને તેથી બનતા અંતઃ યુગ્મકોણોનાં માપ જો સરખાં હોય, તો તે બે રેખાઓ સમાંતર હોય. અહીં, બંને અંતઃ યુગ્મકોણોનાં માપ સરખાં 50°, 50° છે.
∴ l || m
(ii) અહીં, x = 130° (અભિકોણ) વળી, 50° + 130° = 180° બે રેખાઓને એક છેદિકા છે, તો તેથી બનતા છેદિકાની એક જ બાજુના બે અંતઃકોણો પૂરકકોણ હોય, તો તે બે રેખાઓ સમાંતર હોય. અહીં, બંને અંતઃકોણોનાં માપનો સરવાળો 180° છે.
∴ l || m
(iii) l || m છે અને તેને છેદિકા t છેદે છે. તેથી ∠x અને 70° એ બે ખૂણા છેદિકાની એક જ બાજુના અંતઃકોણ છે. આ અંતઃકોણોનાં માપનો સરવાળો 180° થાય.
∴ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°