Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 11 Mensuration Ex 11.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 Mensuration Ex 11.1
Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
Solution:
(a) Side of the square = 60 m
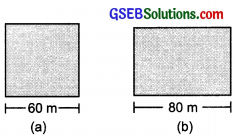
∴ Its perimeter = 4 × Side
= 4 v 60 m = 240 m
Area of the square = Side × Side
= 60 m × 60 m
= 3600 m
(b) ∵ Perimeter of the rectangle = Perimeter of the given square
∴ Perimeter of the rectangle = 240 m
or 2 × [Length + Breadth] = 240 m
or 2 × [80 m + Breadth] = 240 m
or 80 m + Breadth = \(\frac{240}{2}\)m = 120 m
∴ Breadth = (120 – 80)m = 40 m
Now, Area of the rectangle = Length × Breadth
= 80 m × 40 m
= 3200 m2
Since, 3600 m2 × 3200 m2
∴ Area of the square field (a) is greater.
![]()
Question 2.
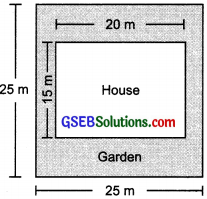
Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m2.
Solution:
∵ The given plot is a square with side as 25 m.
∴ Area of the plot = Side × Side
= 25 m × 25 m
= 625 m2
∵ The constructed portion is a rectangle having length = 20 m and breadth = 15 m.
∴ Area of the constructed portion
= 20 m × 15 m
= 300 m2
Now area of the garden
= [Total plot area] – [Total constructed area]
= (625 – 300) m2
= 325 m2
∴ Cost of developing the garden
= ₹ 55 × 325 = ₹17,875
![]()
Question 3.
The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden? [Lenght of rectangle is 20 – (3.5 + 3.5) metres.]

Solution:
For the semi-circular part:
Diameter of the semi-circle = 7m
∴ Radius of the semi-circle = \(\frac{7}{2}\) = 3.5 m
Area of the 2 semi – circles = 2[\(\frac{1}{2}\) πr2]

Also, perimeter of the 2 semicircles
= 2(\(\frac{2πr}{2}\)) = 2πr = 2 × \(\frac{22}{7}\) × \(\frac{35}{10}\)m = 22m
For rectangular part:
Length of the rectangle = 20 – (3.5 + 3.5)m
= 13 m
Breadth of the rectangle = 7 m
∴ Area = Length × Breadth = 13 m × 7 m
= 91 m2
Perimeter = 2 × [Length + Breadth]
= 2 × [13 m + 0m] = 2 × 13 m = 26 m
Now, Area of the garden = (38.5 + 91)m2
= 129.5 m2
Perimeter of the garden = (38.5 + 91)m2 = 129.5 m2
Perimeter of the garden = 22 m + 26 m = 48 m
![]()
Question 4.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way want to fill up the comers.)
Solution:
Area of a parallelogram
= Base × Corresponding height
Area of a tile = (\(\frac{24}{100}\) × \(\frac{10}{100}\))m2 = \(\frac{240}{10000}\)
m2 = 0.024 m2
∴ Area of the floor = 1080 m2
Now, number of tiles = 
= \(\frac{1080}{0.024}\) = 45000 tiles
![]()
Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle?
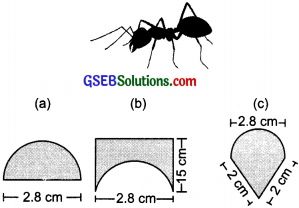
Solution:
(a) Diameter = 2.8 cm
⇒ Radius = \(\frac{2.8}{2}\)
= 1.4 cm
Perimeter of a circle = 2πr
⇒ Perimeter of a semicircle = \(\frac{2πr}{2}\) = πr
∴ Perimeter of the figure = πr + Diameter
= \(\frac{22}{7}\) × 1.4 cm + 2.8 cm
= \(\frac{22}{7}\) × \(\frac{14}{10}\) cm + 2.8 cm
= 4.4 cm + 2.8 cm = 7.2 cm
Note: In this fugure, the diameter is also a part of the figure.
(b) Perimeter of the semi-circular part = πr
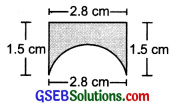
= \(\frac{22}{7}\) × 1.4 cm = 4.4 cm
Perimeter of the remaining part
= 1.5 cm + 28 cm + 1.5 cm = 5.8 cm
∴ Perimeter of the figure
= 4.4 cm + 5.8 cm = 10.2 cm
(c) Perimeter of the semi – circular part

∴ Perimeter of the figure
= 4.4 cm + 2 cm + 2 cm = 8.4 cm
Since, 7.2 cm < 8.4 cm < 10.2 cm
∴ Perimeter of figure ‘b’ has the longest round.
Note: In figures ‘b’ and ‘c’, the diameters are not part of the figures.