GSEB Solutions Class 8 Maths Chapter 11 માપન Ex 11.3

Gujarat Board GSEB Solutions Class 8 Maths Chapter 11 માપન Ex 11.3 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 માપન Ex 11.3

પ્રશ્ન 1.
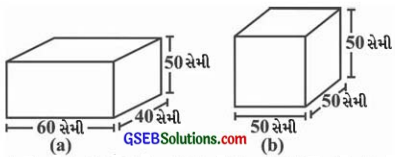
નીચેની આકૃતિમાં બતાવ્યા મુજબના માપનો એક લંબઘન અને એક સમઘન છે. આ બંને ડબામાંથી કયો ડબો બનાવવામાં ઓછી સામગ્રી વપરાશે?

જવાબઃ
(a) લંબઘન ડબાની લંબાઈ (l) = 60 સેમી, પહોળાઈ (b) = 40 સેમી
અને ઊંચાઈ (h) = 50 સેમી છે.
∴ લંબઘન ડબાનું પૃષ્ઠફળ = 2 (lb + bh + hl).
= 2 (60 × 40 + 40 × 50 + 50 × 60)
= 2 (2400 + 2000 + 3000)
= 2 (7400)
= 14,800 સેમી²

(b) સમઘન ડબાની લંબાઈ (l) = 50 સેમી
સમઘન ડબાનું પૃષ્ઠફળ = 6l² = 6 (50)²
= 6 × 50 × 50 = 15,000 સેમી²
આમ, લંબઘન ડબા કરતાં સમઘન ડબાનું પૃષ્ઠફળ વધારે છે.
∴ લંબઘન ડબો બનાવવામાં ઓછી સામગ્રી વપરાશે.

પ્રશ્ન 2.
80 સેમી × 48 સેમી × 24 સેમી માપ ધરાવતી એક સૂટકેસને તાડપત્રીના કપડાથી ઢાંકવાની છે (કવર બનાવવાનું છે). આવપ્રશ્ન પ્રશ્ન પ્રશ્ન 100 સૂટકેસને ઢાંકવા માટે 96 સેમી પહોળાઈ ધરાવતી તાડપત્રીના કેટલા કાપડની જરૂર પડશે?
જવાબઃ
એક સૂટકેસનું પૃષ્ઠફળ શોધીએ.
લંબાઈ (l) = 80 સેમી, પહોળાઈ (b) = 48 સેમી અને ઊંચાઈ (1) = 24 સેમી એક સૂટકેસનું પૃષ્ઠફળ = 2 (lb + bh + hl)
= 2 (80 × 48 + 48 × 24 + 24 × 80)
= 2 (3840 + 1152 + 1920)
= 2 (6912)
= 13,824 સેમી²
આવી 100 સૂટકેસનું પૃષ્ઠફળ = 13,824 × 100 = 13,82,400 સેમી²
1 મીટર કાપડનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 100 × 96 = 9600 સેમી²
∴ 100 સૂટકેસના કવર માટે જરૂરી કાપડ = \(\frac{1382400}{9600}\) = 144 મીટર
આમ, 100 સૂટકેસના કવર માટે 144 મીટર તાડપત્રીનું કાપડ જોઈશે.

પ્રશ્ન 3.
એક એવા સમઘનની બાજુનું માપ શોધો કે જેનું પૃષ્ઠફળ 600 સેમી² હોય?
જવાબઃ
ધારો કે સમઘનની બાજુની લંબાઈ x સેમી છે.
આ સમઘનનું પૃષ્ઠફળ = 6 × x² = 6x²
અહીં સમઘનનું પૃષ્ઠફળ 600 સેમી² આપેલ છે.
∴ 6x² = 600
∴ x² = \(\frac {600}{6}\)
∴ x² = 100
∴ x² = 10²
∴ x = 10
આમ, સમઘનની બાજુની લંબાઈ 10 સેમી છે.

પ્રશ્ન 4.
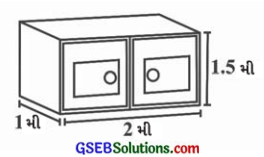
રુખસારે 1 મી × 2 મી × 1.5 મી માપવાળી પેટીને બહારથી રંગ કર્યો. જો તેણે પેટીના તળિયા સિવાય બહારની તરફ બધે રંગ કર્યો હોય, તો તેણે કેટલા પૃષ્ઠફળમાં રંગ કર્યો હશે?

જવાબઃ
પેટીની લંબાઈ (l) = 2 મી, પહોળાઈ (b) = 1 મી અને ઊંચાઈ (h) = 1.5 મી
પેટીનું કુલ પૃષ્ઠફળ = 2(lb + bh + lh)
= 2 (2 × 1 + 1 × 1.5 + 2 × 1.5)
= 2 (2 + 1.5 + 3)
= 2 (6.5) = 13 મી²
પેટીનું તળિયું રંગવાનું નથી. તેની આ પૃષ્ઠફળમાંથી તળિયાનું ક્ષેત્રફળ બાદ કરીશું.
તળિયાનું ક્ષેત્રફળ = l × b = 2 × 1 = 2 મી²
∴ પેટીનો રંગવાનો ભાગ = (13 – 2) મી² = 11 મી²
આમ, રુખસારે પેટીના 11 મી² પૃષ્ઠફળમાં રંગ કર્યો હશે.

પ્રશ્ન 5.
ડેનિયલ એક લંબઘન આકારના ઓરડાની દીવાલ અને છતને રંગે છે જેની લંબાઈ, પહોળાઈ અને ઊંચાઈ ક્રમશઃ 15 મી, 10 મી અને 7 મી છે. રંગના એક ડબામાંથી 100 મીટર² ક્ષેત્રફળ પર રંગ કરી શકાતો હોય, તો ઓરડાને રંગવા માટે કેટલા ડબા રંગ જોઈશે?
જવાબઃ
અહીં લંબઘન ઓરડા માટે, l = 15 મી, b = 10 મી અને h = 7 મી છે.
રંગવાના ભાગનું ક્ષેત્રફળ = ચાર દીવાલોનું ક્ષેત્રફળ + છતનું ક્ષેત્રફળ
= [2 (l + b) × h] + l × b
= [2 (15 + 10) × 7] + 15 × 10
= [2 (25) × 7] + 150
= 350 + 150 = 500 મી²
હવે, 1 ડબામાંથી 100 મી² જેટલું રંગકામ થાય છે.
∴ 500 મી રંગકામ કરવા જરૂરી ડબા = \(\frac {500}{100}\) = 5
આમ, ડેનિયલને ઓરડાને રંગવા માટે 5 ડબા રંગ જોઈશે.

પ્રશ્ન 6.
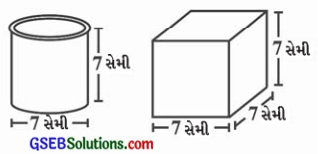
જમણી બાજુ એ આપેલી આકૃતિમાંના બંને ડબા કઈ રીતે સમાન છે અને કઈ રીતે એક બીજાથી જુદા પડે છે? કયા ડબાનું સેમીન પાર્થ પૃષ્ઠફળ વધારે હશે?

જવાબઃ
બંને ચિત્રોમાં એક ડબો નળાકાર છે અને બીજો ડબો સમઘન છે.
બંનેમાં સામ્યતા : બંનેની ઊંચાઈ સરખી છે.
બંનેમાં તફાવત: એક નળાકાર છે બીજો સમઘન છે.
: નળાકાર ડબામાં આડી સપાટી વર્તુળાકાર વક્ર છે.
: સમઘન ડબામાં બધી એકરૂપ ચોક્કસ સપાટી છે.
નળાકાર ડબાનું પાર્શ્વ પૃષ્ઠફળ એટલે કે વક્રસપાટીનું ક્ષેત્રફળ
= 2πrh
= 2 × \(\frac {22}{7}\) × \(\frac {7}{2}\) × 7
= 22 × 7
= 154 સેમી²
સમઘન ડબાનું પાર્શ્વ પૃષ્ઠફળ = 4l²
= 4 × 7²
= 4 × 49
= 196 સેમી²
આમ, સમઘન ડબાનું પાર્શ્વ પૃષ્ઠફળ વધારે છે.

પ્રશ્ન 7.
7 મીટર ત્રિજ્યા અને ૩ મીટર ઊંચાઈવાળી એક બંધ નળાકાર ટાંકી ધાતુના પતરામાંથી બનાવવામાં આવેલ છે. આ ટાંકીને બનાવવા માટે ધાતુનું કેટલું પતરું જોઈશે?
જવાબઃ
બંધ નળાકાર ટાંકીની ત્રિજ્યા (r) = 7 મી અને ઊંચાઈ (h) = 3 મી
બંધ નળાકાર ટાંકીનું પૃષ્ઠફળ = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 7 (7 + 3)
= 44(10)
= 440 મી²
આમ, બંધ નળાકાર ટાંકી બનાવવા 440 મી² ધાતુનું પતરું જોઈશે.

પ્રશ્ન 8.
એક ખુલ્લા નળાકારની વક્ર સપાટીનું ક્ષેત્રફળ 4224 સેમી² છે. આ નળાકારને તેની ઊંચાઈ તરફથી કાપીને 33 સેમી પહોળાઈની એક લંબચોરસ આકારની સીટ બનાવવામાં આવે છે, તો લંબચોરસ સીટની પરિમિતિ મેળવો.
જવાબઃ
ખુલ્લા નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = 4224 સેમી² છે.
ધારો કે નળાકારમાંથી બનતા લંબચોરસ આકારની સીટની લંબાઈ l સેમી છે.
∴ l × b = 4224
∴ l × 33 = 4224
∴ l = \(\frac {4224}{33}\) = 128 સેમી
લંબચોરસ આકારની સીટની લંબાઈ 128 સેમી હોય.
લંબચોરસ સીટની પરિમિતિ = 2 (l + b)
= 2 (128 + 33)
= 2 (161) = 322 સેમી
આમ, લંબચોરસ સીટની પરિમિતિ 322 સેમી છે.

પ્રશ્ન 9.
એક રસ્તાને એક વખત સમતલ કરવા માટે રોલરને 750 વખત પરિભ્રમણ કરવું પડે છે. હવે જો રોલરનો વ્યાસ 84 સેમી અને પહોળાઈ 1 મીટર હોય, તો રસ્તાનું ક્ષેત્રફળ શોધો.
જવાબઃ

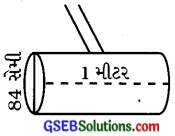
રોલરનો આકાર નળાકાર હોય છે.
રોલરની ત્રિજ્યા = વ્યાસ ÷ 2 = \(\frac {84}{2}\) = 42 સેમી
લરની લંબાઈ (ઊંચાઈ) = 1 મી = 100 સેમી
રોલરની વક્રસપાટીનું ક્ષેત્રફળ = 2πrh
= 2 × \(\frac {22}{7}\) × 42 × 100
= 26,400 સેમી²
રોલર એક પરિભ્રમણમાં 26,400 સેમી² ક્ષેત્રફળ આવરી લે છે.
રોલર વડે 750 પરિભ્રમણમાં આવરી લેવાતું ક્ષેત્રફળ
= 26,400 × 750 સેમી²
રોલરે 750 પરિભ્રમણમાં આવરેલું ક્ષેત્રફળ = \(\frac{26400 \times 750}{100 \times 100}\) મી²
= 1980 મી²
આમ, રસ્તાનું ક્ષેત્રફળ 1980 મી² છે.

પ્રશ્ન 10.
એક કંપની તેના દૂધ પાવડરને એવા નળાકાર ડબામાં પૅક કરે છે જેનો વ્યાસ 14 સેમી અને ઊંચાઈ 20 સેમી હોય. બાજુની આકૃતિમાં બતાવ્યા પ્રમાણે કંપની ડબાની વક્રસપાટી પર ફરતે લેબલ લગાવે છે. જો આ લેબલ નળાકારના શીર્ષ અને તળિયા બનેથી 2 સેમી દૂર ચોંટાડવામાં આવતું હોય, તો લેબલનું ક્ષેત્રફળ શોધો.

જવાબઃ
નળાકાર ડબા ઉપર લગાવેલ લેબલ પણ નળાકાર હોય.
નળાકારનો વ્યાસ = 14 સેમી
∴ નળાકારની ત્રિજ્યા = 7 સેમી
હવે, લેબલની ત્રિજ્યા (r) પણ 7 સેમી થાય.
લેબલ ડબાના તળિયેથી 2 સેમી ઉપર અને શીર્ષથી 2 સેમી નીચે છે.
∴ લેબલની ઊંચાઈ = ડબાની ઊંચાઈ – (2 + 2) સેમી
= 20 સેમી – 4 સેમી = 16 સેમી
નળાકાર લેબલનું ક્ષેત્રફળ = 2πrh
= 2 × \(\frac {22}{7}\) × 7 × 16
= 44 × 16
= 704 સેમી²
આમ, લેબલનું ક્ષેત્રફળ 704 સેમી² છે.