GSEB Solutions Class 8 Maths Chapter 11 Mensuration Ex 11.4

Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 11 Mensuration Ex 11.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 Mensuration Ex 11.4

Question 1.
Given a cylindrical tank, in which situation will you find surface area and in which situation volume?
(a) To find how much it can hold?
(b) Number of cement bags required to plaster it?
(c) To find the number of smaller tanks that can be filled with water from it?

Solution:
(a) Volume
(b) Surface area
(c) Volume

Question 2.
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cyclinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

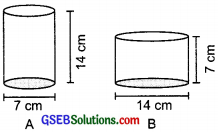
Solution:
In volume of a cylinder, the radius is multiplied by squaring it.
∴ Volume of cylinder B will be more than that of A.
Volume of cylinder A
Radius (r) = cm. Height (h) = 14 cm
∴ Volume of a cylinder A = πr²h
= \(\frac{22}{7}\) × (\(\frac{7}{2}\))² × 14 cm³
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 14 cm³
= 11 × 7 × 7 cm³ = 539 cm³
Volume of cyclinder B
Radius (r) = \(\frac{14}{2}\) = 7 cm Height (h) = 7 cm
∴ Volume of the cylinder B = πr²h
= \(\frac{22}{7}\) × (7)² × 7 cm³ = \(\frac{22}{7}\) × 7 × 7 × 7 cm³
= 22 × 7 × 7 = 1078 cm³
Thus, cylinder B has greater volume.
Now,
Surface area of cylinder A = 2 × π × r × (r + h)
= 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × [\(\frac{7}{2}\) + 14] cm²
= 22 × \(\frac{35}{2}\) cm² = 11 × 35 cm² = 385 cm²
Surface area of cylinder B = 2πrh(r + h)
= 2 × \(\frac{22}{7}\) × 7 × [7 + 7] cm²
= 2 × 22 × [14] cm² = 616 cm²
Thus, the cylinder of greater capacity has greater (more) surface area.

Question 3.
Find the height of a cuboid whose base area is 180 cm² and volume is 900 cm³?
Solution:
Let the height of the cuboid = h cm
∴ Base area × Height = Volume
or 180 × h = 900
or h = \(\frac{900}{180}\) = 5 cm
Hence, the required height of the cuboid = 5 cm

Question 4.
A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can he placed in the given cuboid?
Solution:
Volume of the cuboid
= 60 cm × 54 cm × 30 cm
= (60 × 54 × 30) cm³
Volume of the small cube = (6 × 6 × 6) cm³

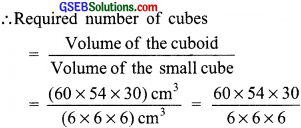
= 10 × 9 × 5 = 450
Thus, 450 small cubes can be placed in the given cuboid.

Question 5.
Find the height of the cylinder whose volume is 1.54 m³ and diameter of the base is 140 cm?
Solution:
Diameter = 140 cm
⇒ Radius (r) = \(\frac{140}{2}\) = 70 cm
Let height of the cylinder be h m.
∴ Volume = πr²h = \(\frac{22}{7}\) × (70)² × h
= \(\frac{22}{7}\) × 70 × 70 × h
Since, volume of the cylinder is 1.54 m³.
∴ 22 × 10 × 70 × h = 1.54 × 1000000
= 1540000
or h = \(\frac{1540000}{22×10×70}\) = 100 cm or 1.

Question 6.
A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in lit tank?
Solution:

Radius = 1.5 m = \(\frac{15}{10}\) m
Height = 7m
∴ Volume of the tank = πr²h
= \(\frac{22}{7}\) × (\(\frac{15}{10}\))² × 7 m³
= \(\frac{22}{7}\) × \(\frac{15}{10}\) × \(\frac{15}{10}\) × 7 m³
= \(\frac{11×3×3}{2}\) m³ = \(\frac{99}{2}\) m³ = 49.5 m³
∵ 1 m³ = 1000 litres
∴ Quantity of milk in the tank
= 49.5 × 1000 litres
= \(\frac{495}{10}\) × 1000 litres = 49500 litres

Question 7.
If each of a cube is doubled,
(i) How many times will its surface area increase?
(ii) How many times will its volume increase?
Solutoion:
Let the original edge be x
∴ Increased edge = 2x

(i) ∴ Original S.A. = 6x²
Increased SA. = 6(2x)² = 24x²
Since, \(\frac{24 x^{2}}{6 x^{2}}\) = 4
∴ Surface area is increased by 4 times

(ii) Original volume = x³
Increased volume = (2x)³ = 8x³
∵ \(\frac{8 x^{3}}{x^{3}}\) = 8
∴ Volume is increased by 8 times.

Question 8.
Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m³, find the number of hours it will take to fill the reservoir?
Solution:
Volume of the reservoir
= 108 m³

∵ 1 m³ = 1000 litres
∴ Capacity of the reservoir
108 × 1000 litres = 108000 litres
Amount of water poured in 1 minute
= 60 litres
∴ Amount of water to be poured in 1 hour
= 60 × 60 litres
Thus, number of hours required to fill the reservoir = \(\frac{108000}{60×60}\) = 30
∴ The required number of hours = 30