GSEB Solutions Class 8 Maths Chapter 11 માપન InText Questions

Gujarat Board GSEB Solutions Class 8 Maths Chapter 11 માપન InText Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 માપન InText Questions

પાઠ્યપુસ્તકમાંથી: (પાઠ્યપુસ્તક પાન નંબર . 170)

1.

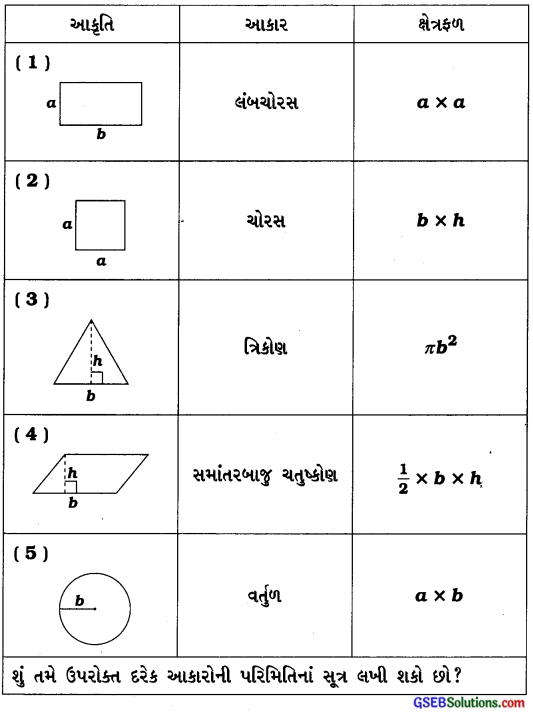
જવાબ:
1. લંબચોરસ → a × b
2. ચોરસ → a × a
3. ત્રિકોણ → \(\frac {1}{2}\) × b × h
4. સમાંતરબાજુ ચતુષ્કોણ → b × h
5. વર્તુળ → πb²

હા. હું ઉપરોક્ત દરેક આકારોની પરિમિતિનાં સૂત્ર લખી શકું છું. તે નીચે મુજબ છે :
1. લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
2. ચોરસની પરિમિતિ = 4 x લંબાઈ
3. ત્રિકોણની પરિમિતિ = ત્રણે બાજુઓનાં માપનો સરવાળો
4. સમાંતરબાજુ ચતુષ્કોણની પરિમિતિ = 2 (પાસપાસેની બે બાજુઓનાં માપનો સરવાળો)
5. વર્તુળની પરિમિતિ (પરિઘ) = 2πr

પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર .170)

(a) નીચે આપેલા આકારોને બૉક્સમાં આપેલાં ક્ષેત્રફળ સાથે યોગ્ય રીતે જોડોઃ

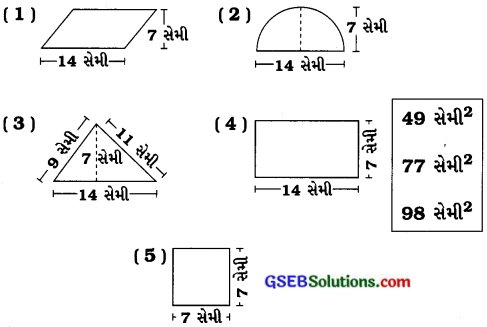
જવાબ:

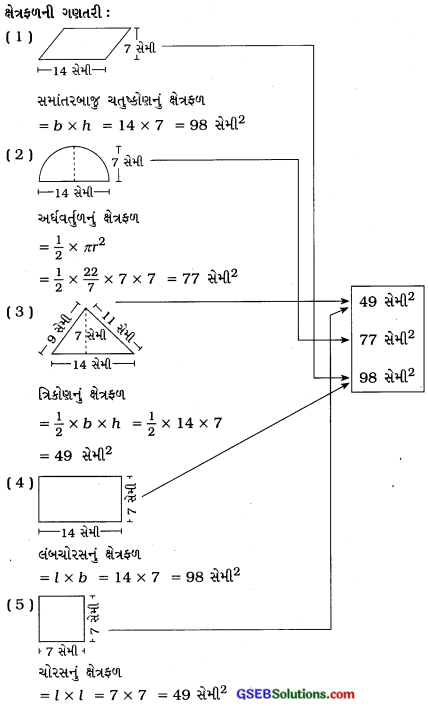
(b) ઉપર દર્શાવેલા દરેક આકારની પરિમિતિ લખોઃ
જવાબઃ
1. સમાંતરબાજુ ચતુષ્કોણની પરિમિતિ = 2 (14 + 7) સેમી
= 2 (21) સેમી = 42 સેમી
2. અર્ધવર્તુળની પરિમિતિ = πr + 2r
= \(\frac {22}{7}\) × 7 + 2 × 7 = 22 + 14
= 36 સેમી
3. ત્રિકોણની પરિમિતિ = ત્રણે બાજુઓનાં માપનો સરવાળો
= 14 + 1 + 9 = 34 સેમી
4. લંબચોરસની પરિમિતિ = 2 (l + b)
= 2 (14 + 7) = 2 × 21 = 42 સેમી
5. ચોરસની પરિમિતિ = 4l
= 4 × 7 = 88 સેમી

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 172)

1. નઝમાની બહેન પાસે પણ એક સમલંબ આકારનો પ્લૉટ છે. જે આકૃતિમાં દર્શાવેલ છે. આ પ્લૉટને આકૃતિમાં બતાવ્યા મુજબ ત્રણ ભાગમાં વિભાજિત કરો. હવે આ સમલંબ ચતુષ્કોણ WXYZનું ક્ષેત્રફળ = \(\frac{h(a+b)}{2}\) છે તેમ દર્શાવો.

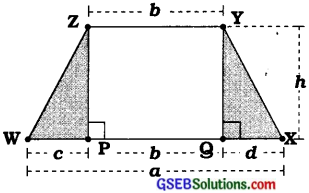
જવાબ:
∆ PWZનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × પાયો × વેધ
= \(\frac {1}{2}\) × c × h
= \(\frac {1}{2}\)ch
લંબચોરસ PQYZનું ક્ષેત્રફળ = લંબાઈ x પહોળાઈ
= b × h
= bh

∆ QXYનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × d x h
= \(\frac {1}{2}\)dh
હવે, સમલંબ ચતુષ્કોણ WXYZનું ક્ષેત્રફળ
= ∆ PWZનું ક્ષેત્રફળ + લંબચોરસ PQYZનું ક્ષેત્રફળ + ∆ QXYનું ક્ષેત્રફળ
= \(\frac {1}{2}\)ch + bh + \(\frac {1}{2}\)dh
= \(\frac {1}{2}\)ch + \(\frac {1}{2}\)dh + bh
= \(\frac {1}{2}\)(c + d) h + bh
= \(\frac {1}{2}\)(a – b)h + bh (∵ c + d = a – b)
= [\(\frac {1}{2}\)(a – b) + b]h
= [\(\frac{a-b}{2}\) + b]h
= [latex]\frac{a-b+2 b}{2}[/latex]h
= \(\frac{h(a+b)}{2}\)
આમ, સમલંબ ચતુષ્કોણ WXYZ = \(\frac{h(a+b)}{2}\)

2. જો n = 10 સેમી, c = 6 સેમી, b = 12 સેમી અને d = 4 સેમી હોય, તો પ્લૉટના દરેક ભાગનું ક્ષેત્રફળ અલગ અલગ શોધો અને સમલંબ પ્લૉટનું કુલ ક્ષેત્રફળ મેળવવા માટે આ ભાગનો સરવાળો કરો. ત્યારબાદ સૂત્ર \(\frac{h(a+b)}{2}\)માં h, a અને bની કિંમત મૂકીને જવાબનો તાળો મેળવો.
જવાબઃ
હવે, h = 10 સેમી, c = 6 સેમી, b = 12 સેમી અને d = 4 સેમી લઈ જવાબ મેળવીએ.
∆ PWZનું ક્ષેત્રફળ = \(\frac {1}{2}\)ch
= \(\frac {1}{2}\) × 6 × 10 = 30 સેમી²
∆ QXYનું ક્ષેત્રફળ = latex]\frac {1}{2}[/latex]dh
= latex]\frac {1}{2}[/latex] × 4 × 10 = 20 સેમી²
લંબચોરસ PQYZનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 12 × 10 = 120 સેમી²
∴ સમલંબ ચતુષ્કોણ WXYZનું ક્ષેત્રફળ
= ∆ PWZનું ક્ષેત્રફળ + ∆ QXYનું ક્ષેત્રફળ + લંબચોરસ PQYZનું ક્ષેત્રફળ
= 30 સેમી² + 20 સેમી² + 120 સેમી²
= 170 સેમી²
હવે, સમલંબ ચતુષ્કોણ WXYZનું ક્ષેત્રફળ
= \(\frac{h(a+b)}{2}\)
= \(\frac{10(22+12)}{2}\)
= \(\frac{10(34)}{2}\)
= 170 સેમી
a = c + b + d
= 6 + 12 + 4
= 22સેમી
આમ, સમલંબ ચતુષ્કોણના ક્ષેત્રફળની ચકાસણી બંને રીતે થઈ.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 173)

1. આકૃતિમાં બતાવેલા સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ શોધોઃ

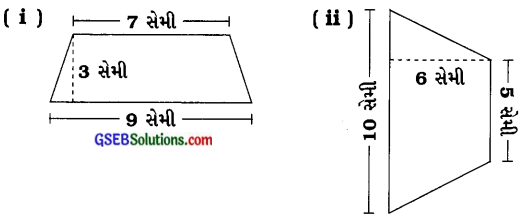
જવાબ:
નોંધઃ સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
(i) આપેલા સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (9 + 7) × 3
= [late/8x]\frac {1}{2}[/latex] × 16 × 3 = 24 સેમી²
(ii) આપેલા સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (10 + 5) × 6
= \(\frac {1}{2}\) × 15 × 6
= 45 સેમી²

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 174)

1. આપણે જાણીએ છીએ કે સમાંતરબાજુ ચતુષ્કોણ પણ એક ચતુષ્કોણ જ છે, તો ચાલો આ સમાંતરબાજુ ચતુષ્કોણનો એક વિકર્ણ દોરી તેને બે ત્રિકોણોમાં વિભાજિત કરીએ અને તે બંને ત્રિકોણનાં ક્ષેત્રફળ શોધીએ. આ રીતે સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ પણ મેળવી શકાય. શું સમાંતર ચતુષ્કોણનું ક્ષેત્રફળ શોધવાનું સૂત્ર આગળ મેળવેલ સૂત્ર સાથે સામ્ય ધરાવે છે?

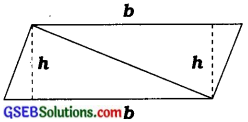
જવાબ:
આપણે જાણીએ છીએ કે સમાંતરબાજુ ચતુષ્કોણનો વિકર્ણ ચતુષ્કોણને બે ત્રિકોણમાં વહેચે છે.
ચતુષ્કોણ XYZwનું ક્ષેત્રફળ
= ∆XYWનું ક્ષેત્રફળ + ∆YZWનું ક્ષેત્રફળ
= (\(\frac {1}{2}\)b × h) + (\(\frac {1}{2}\)b × h)
= 2(\(\frac {1}{2}\)b × h)
= bh

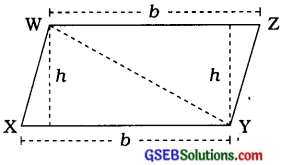
હવે, ખરેખર તો ☐ XYZW એ સમાંતરબાજુ ચતુષ્કોણ છે.
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = પાયો × પાયા પરનો વેધ વળી, સમાંતરબાજુ ચતુષ્કોણ એ સમલંબ ચતુષ્કોણ પણ છે.
સમલંબ ચતુષ્કોણ XYZWનું ક્ષેત્રફળ = \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (b + b) × h
= \(\frac {1}{2}\) × 2b × h = bh
આમ, સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ
હા, સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ શોધવાનું સૂત્ર આગળ મેળવેલા સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ શોધવાના સૂત્ર સાથે સામ્ય ધરાવે છે.

વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબર . 175)

1. સમાંતરબાજુ ચતુષ્કોણનો વિકર્ણ દોરી તેને એકરૂપ ત્રિકોણોમાં વહેંચી શકાય છે. શું સમલંબ ચતુષ્કોણને પણ આ રીતે વિકર્ણ દ્વારા વિભાજિત કરવાથી બે એકરૂપ ત્રિકોણ પ્રાપ્ત થશે?
જવાબ:
ના, સમલંબ ચતુષ્કોણને ગમે તે એક વિકર્ણ દ્વારા વિભાજિત કરવાથી બે એકરૂપ ત્રિકોણો પ્રાપ્ત ન થાય.

જુઓ સમલંબ ચતુષ્કોણ ABCDનાં વિકર્ણો દોરતાં મળતાં ત્રિકોણો એકરૂપ નથી.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 175)

1. નીચે દોરેલા ચતુષ્કોણોનાં ક્ષેત્રફળ શોધોઃ

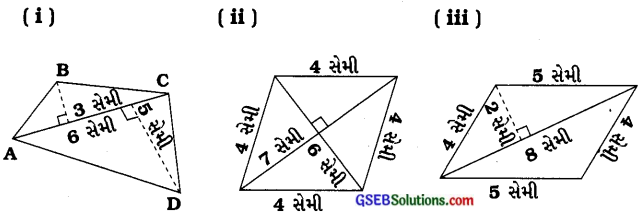
જવાબ:
(i) અહીં આપેલી આકૃતિ ચતુષ્કોણની છે.
ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = \(\frac {1}{2}\) × વિકર્ણ × વિકર્ણ પરના બે વેધનો સરવાળો
= \(\frac {1}{2}\) × d × (h₁ + h₂)
= \(\frac {1}{2}\) × 6 × (3 + 5)
= 3 (8) = 24 સેમી²

(ii) અહીં આપેલી આકૃતિ સમબાજુew ચતુષ્કોણની છે. તેમાં વિકર્ણ d₁ = 7 સેમી, વિકર્ણ d₂ = 6 સેમી
સમબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × બે વિકણનો ગુણાકાર
= \(\frac {1}{2}\) × d₁ × d₂
= \(\frac {1}{2}\) × 7 × 6
= 7 × 3 = 21 સેમી²

(iii) અહીં આપેલી આકૃતિ સમાંતરબાજુ ચતુષ્કોણની છે.
સમાંતરબાજુ ચતુષ્કોણમાં વિકર્ણ વડે બનતા બે ત્રિકોણ એકરૂપ અને સમક્ષેત્ર હોય છે. વિભાજન થાય છે.
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = 2 × કોઈ એક ત્રિકોણનું ક્ષેત્રફળ
= 2 × (\(\frac {1}{2}\) × 8 × 2)
= 2 × 8 = 16 સેમી²

પ્રયત્ન કરોઃ (પાઠ્યપુસ્તક પાન નંબર . 176)

(i) નીચેની આકૃતિમાં દર્શાવેલા બહુકોણનાં ક્ષેત્રફળ મેળવવા માટે તેને ત્રિકોણ અને સમલંબ ચતુષ્કોણમાં વિભાજિત કરોઃ

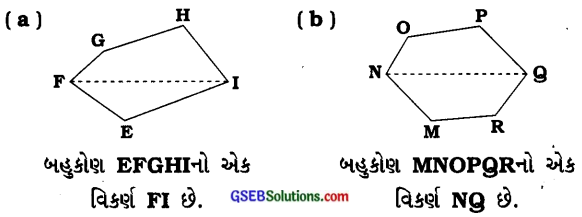
જવાબ:
(a) આપણે FI વિકર્ણ ઉપર લંબ દોરીએ.

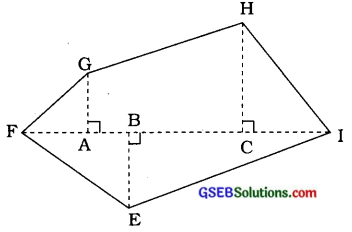
અને GA ⊥ FI, EB ⊥ FI
અને HC ⊥ FI દોર્યા છે.
બહુકોણ EGHIનું ક્ષેત્રફળ = ∆ GFAનું ક્ષેત્રફળ + ચતુષ્કોણ ACHGનું ક્ષેત્રફળ + ∆ HCIનું ક્ષેત્રફળ + ∆ BIEનું ક્ષેત્રફળ + ∆ FBEનું ક્ષેત્રફળ
= [\(\frac {1}{2}\) × FA × GA] + [\(\frac {1}{2}\)(AG + CH) × AC] + [\(\frac {1}{2}\) × CI × HC] + [\(\frac {1}{2}\) × BI × BE] + [\(\frac {1}{2}\) × FB × BE

(b)

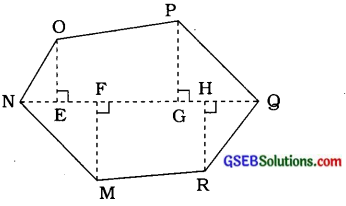
આપણે \(\overline{\mathrm{NQ}}\) વિકર્ણ ઉપર લંબ દોરીએ.
\(\overline{\mathrm{OE}}\) ⊥ \(\overline{\mathrm{NQ}}\), \(\overline{\mathrm{MF}}\) ⊥ \(\overline{\mathrm{NQ}}\), \(\overline{\mathrm{PG}}\) ⊥ \(\overline{\mathrm{NQ}}\) અને \(\overline{\mathrm{RH}}\) ⊥ \(\overline{\mathrm{NQ}}\)
બહુકોણ MNOPQRનું ક્ષેત્રફળ
= ∆ NEOનું ક્ષેત્રફળ + સમલંબ ચતુષ્કોણ EGPOનું ક્ષેત્રફળ + ∆ GQPનું ક્ષેત્રફળ + ∆ HQRનું ક્ષેત્રફળ + સમલંબ ચતુષ્કોણ MRHFનું ક્ષેત્રફળ + ∆ NFMનું ક્ષેત્રફળ
= [\(\frac {22}{7}\) × NE × OE] + [\(\frac {1}{2}\) × (EG + OP) × EG] + [\(\frac {1}{2}\) × GQ × PG] + [\(\frac {1}{2}\) × (FM + HR) × FH] + [\(\frac {1}{2}\) × NF × FM]

(ii) બહુકોણ ABCDEને આકૃતિમાં દર્શાવ્યા મુજબ જુદા જુદા ભાગોમાં વિભાજિત કરવામાં આવેલ છે. અહીં AD = 8 સેમી, AH = 6 સેમી, AG = 4 સેમી, AF = 3 સેમી અને લંબ BF = 2 સેમી, CH = 3 સેમી, EG = 2.5 સેમી આપવામાં આવેલ છે, તો બહુકોણનું ક્ષેત્રફળ શોધો.
બહુકોણ ABCDEનું ક્ષેત્રફળ = ∆ APBનું ક્ષેત્રફળ + ………………
∆ AFBનું ક્ષેત્રફળ = \(\frac {1}{2}\) × AF × BF = \(\frac {1}{2}\) × 3 × 2 = …………
સમલંબ ચતુષ્કોણ FBCHનું ક્ષેત્રફળ = FH × \(\frac{(\mathrm{BF}+\mathrm{CH})}{2}\)
= 3 × \(\frac{(2+3)}{2}\) (FH = AH – AF)
∆ CHDનું ક્ષેત્રફળ = \(\frac {1}{2}\) × HD × CH = ……….
∆ ADEનું ક્ષેત્રફળ = \(\frac {1}{2}\) × AD × GE = ………..
તેથી, બહુકોણ ABCDEનું ક્ષેત્રફળ =………………….

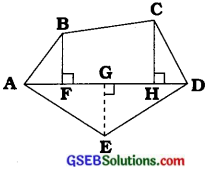
જવાબ:

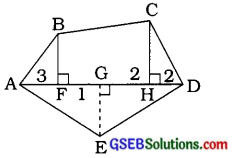
આકૃતિ માટે:
AD = 8 સેમી, AH = 6 સેમી, HD = 2 સેમી, AG = 4 સેમી, GD = 4 સેમી, AF = 3 સેમી અને GF = 1 સેમી છે.
બહુકોણ ABCDEનું ક્ષેત્રફળ = ∆ AFBનું ક્ષેત્રફળ + સમલંબ ચતુષ્કોણ FBCHનું ક્ષેત્રફળ + ∆ CHDનું ક્ષેત્રફળ + ∆ ADEનું ક્ષેત્રફળ
હવે, ∆ AFBનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × AF × BF
= \(\frac {1}{2}\) × 3 × 2 = 3 સેમી²
સમલંબ ચતુષ્કોણ FBCHનું ક્ષેત્રફળ = FH × \(\frac{(\mathrm{BF}+\mathrm{CH})}{2}\)
= 3 × \(\frac{(2+3)}{2}\) [∵ FH = AH – AF]
= 3 × \(\frac {5}{2}\) = \(\frac {15}{2}\) = 7.5 સેમી²
∆ CHDનું ક્ષેત્રફળ = \(\frac {1}{2}\) × HD × CH
= \(\frac {1}{2}\) × (AD – AH) × CH [∵ HD = AD – AH]
= \(\frac {1}{2}\) × (8 – 6) × 3
= \(\frac {1}{2}\) × 2 × 3 = 3 સેમી²
∆ ADEનું ક્ષેત્રફળ = \(\frac {1}{2}\) × AD × GE
= \(\frac {1}{2}\) × 8 × 2.5
= 4 × 2.5 = 10 સેમી²
આમ, બહુકોણ ABCDEનું ક્ષેત્રફળ = ∆ AFBનું ક્ષેત્રફળ + સમલંબ ચતુષ્કોણ FBCHનું ક્ષેત્રફળ + ∆ CHDનું ક્ષેત્રફળ + ∆ ADEનું ક્ષેત્રફળ
= (3 + 7.5 + 3 + 10) સેમી²
= 23.5 સેમી²

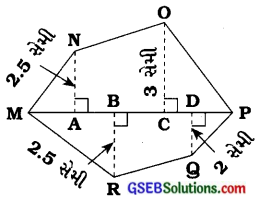
(iii) આકૃતિમાં દર્શાવેલ બહુકોણ MNOPQRમાં જો MP = 9 સેમી, MD = 7 સેમી, MC = 6 સેમી, MB = 4 સેમી અને MA = 2 સેમી
હોય, તો બહુકોણનું ક્ષેત્રફળ શોધો. NA, OC, QD અને RB અ MP દોરેલા લંબ છે.

જવાબઃ

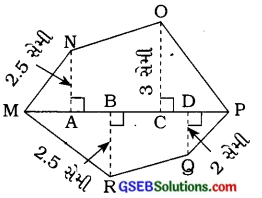
આકૃતિ માટે:
MP = 9 સેમી, MD = 7 સેમી,
∴ DP = 2 સેમી
MC = 6 સેમી, ∴ CP = 3 સેમી
MB = 4 સેમી, ∴ BP = 5 સેમી
MA = 2 સેમી ∴ AC = MC – MA = 6 – 2 સેમી = 4 સેમી
MB + BD = MD ∴ BD = 7 – 4 સેમી = 3 સેમી
∆ MANનું ક્ષેત્રફળ = \(\frac {1}{2}\) × MA x AN
= \(\frac {1}{2}\) × 2 × 2.5 = 2.5 સેમી²
સમલંબ ચતુષ્કોણ ACONનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (AN + OC) × AC
= \(\frac {1}{2}\) × (2.5 + 3) × 4
= (5.5) × 2 = 11 સેમી²
∆ CPOનું ક્ષેત્રફળ = \(\frac {1}{2}\) × CP × CO
= \(\frac {1}{2}\) × 3 × 3
= \(\frac {9}{2}\) = 4.5 સેમી²
∆ MBRનું ક્ષેત્રફળ = \(\frac {1}{2}\) × MB × BR
= \(\frac {1}{2}\) × 4 × 2.5
= 2 × 2.5 = 5 સેમી²
સમલંબ ચતુષ્કોણ BRQDનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (BR + DQ) × BD
= \(\frac {1}{2}\) × (2.5 + 2) × 3
= \(\frac {1}{2}\) × 4.5 × 3 = 6.75 સેમી²
∆ DQPનું ક્ષેત્રફળ = \(\frac {1}{2}\) × DP × DQ
= \(\frac {1}{2}\) × 2 × 2
= 1 × 2 = 2 સેમી²
આમ, બહુકોણ MNOPQRનું ક્ષેત્રફળ
= ∆ MANનું ક્ષેત્રફળ + સમલંબ ચતુષ્કોણ ACONનું ક્ષેત્રફળ + ∆ CPOનું ક્ષેત્રફળ + ∆ MBRનું ક્ષેત્રફળ + સમલંબ ચતુષ્કોણ BRQDનું ક્ષેત્રફળ + ∆ DQPનું ક્ષેત્રફળ
= 2.5 સેમી² + 11 સેમી² + 4.5 સેમી² + 5 સેમી² + 6.75 સેમી² + 2 સેમી²
= 31.75 સેમી²

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર . 180)

1. અહીં આપેલી આકૃતિમાં આપેલા ઘનાકારને નળાકાર કહેવો એ કંઈ ખોટું છે?

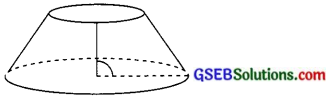
જવાબઃ
અહીં આપેલ ઘનાકારને નળાકાર કહી ન શકાય, કારણ કે –
1. નળાકારને ઉપર અને નીચે વર્તુળાકાર એકરૂપ સમાંતર બે સપાટી હોય છે.
2. નળાકારને ઊભી વક્રસપાટી સરખી ત્રિજ્યાની હોય છે.

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર . 181)

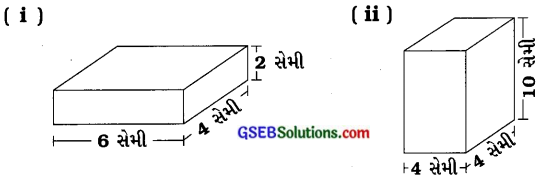
1. આકૃતિમાં દર્શાવેલ લંબઘનનું પૃષ્ઠફળ મેળવોઃ

જવાબ:
(i) આકૃતિમાં આપેલા લંબઘન માટે –
લંબાઈ l = 6 સેમી, પહોળાઈ b = 4 સેમી અને ઊંચાઈ h = 2 સેમી
લંબઘનનું કુલ પૃષ્ઠફળ = 2(lb + bh + hl)
= 2 (6 × 4 + 4 × 2 + 2 × 6)
= 2 (24 + 8 + 12).
= 2 (44)
= 88 સેમી²

(ii) આકૃતિમાં આપેલા લંબઘન માટે –
લંબાઈ l = 4 સેમી, પહોળાઈ b = 4 સેમી અને ઊંચાઈ h = 10 સેમી
લંબઘનનું કુલ પૃષ્ઠફળ = 2 (lb + bh + hl)
= 2 (4 × 4 + 4 × 10 + 10 × 4)
= 2 (16 + 40 + 40)
= 2 (96) = 192 સેમી²

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર .181)

1. શું આપણે કહી શકીએ કે લંબઘનનું કુલ પૃષ્ઠફળ = પાર્શ્વ પૃષ્ઠફળ + 2 (તળિયાનું ક્ષેત્રફળ)?
જવાબઃ
હા, લંબઘનનું કુલ પૃષ્ઠફળ = પાર્શ્વ પૃષ્ઠફળ + 2 (તળિયાનું ક્ષેત્રફળ)
(નોંધઃ લંબઘનના તળિયાનું ક્ષેત્રફળ અને મથાળાનું સપાટીનું ક્ષેત્રફળ સરખું હોય છે.]

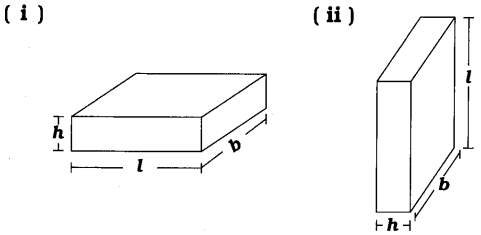
2. જો આકૃતિ (i)માં દર્શાવેલા લંબઘનની ઊંચાઈ અને આધારની લંબાઈને પરસ્પર બદલી નાખીએ તો આકૃતિ (i)માં દર્શાવેલ લંબઘન પ્રાપ્ત થાય છે, તો તેનું પાર્શ્વ પૃષ્ઠીય ક્ષેત્રફળ બદલાઈ જશે?

જવાબ:

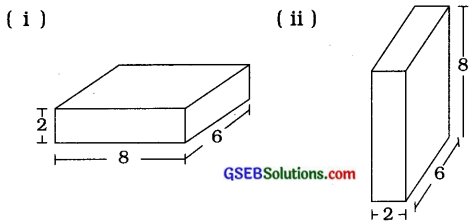
(i) આ લંબઘનનું પાર્શ્વ પૃષ્ઠીય ક્ષેત્રફળ = 2 (l + b) × h
(ii) આ લંબઘનનું પાર્શ્વ પૃષ્ઠીય ક્ષેત્રફળ = 2 (h + b) × l
આમ, સ્પષ્ટ છે કે ક્ષેત્રફળોનાં માપ જુદાં જુદાં મળે.
આમ, ઊંચાઈ અને આધારની લંબાઈ પરસ્પર બદલતાં પાર્શ્વ પૃષ્ઠીય ક્ષેત્રફળ બદલાઈ જાય છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 182)

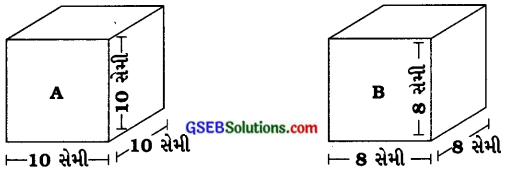
1. આકૃતિમાં દર્શાવેલ ઘન Aનું પૃષ્ઠફળ અને ઘન Bનું પાર્શ્વ પૃષ્ઠફળ શોધોઃ

જવાબ:
ઘન A માટે (અહીં પૃષ્ઠફળ શોધવાનું છે.)
ઘનની બાજુની લંબાઈ (l) = 10 સેમી
∴ ઘનનું પૃષ્ઠફળ = 6l²
= 6 × 10² = 6 × 100 = 600 સેમી²
ઘન B માટે: (અહીં પાર્શ્વ પૃષ્ઠફળ શોધવાનું છે.)
ઘનની બાજુની લંબાઈ (l) = 8 સેમી
∴ ઘનનું પાર્શ્વ પૃષ્ઠફળ = 4l²
= 4 × 8² = 4 × 64 = 256 સેમી²

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર . 183)

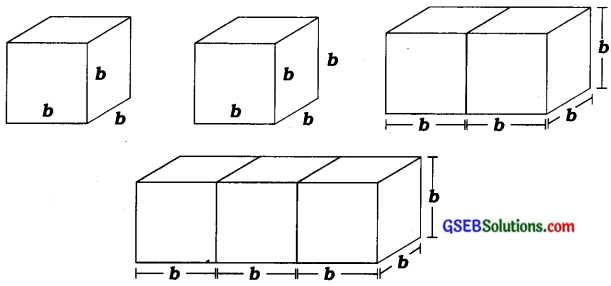
1. આકૃતિમાં દર્શાવ્યા મુજબ b બાજુવાળા બે ઘનને જોડીને એક લંબઘન બનાવ્યો છે, તો આ લંબઘનનું પૃષ્ઠફળ શું હશે? શું એ 12b² હશે? શું આવી જ રીતે b બાજુ ધરાવતાં ત્રણ ઘન જોડીને બનાવેલ લંબઘનનું પૃષ્ઠફળ 18b² થશે? કેમ?

જવાબઃ
(i) જ્યારે બે ઘનને એકબીજા સાથે બરોબર જોડવામાં આવે છે, ત્યારે નવો આકાર લંબઘન થશે.
જેની લંબાઈ = b + b = 2b, પહોળાઈ = b અને ઊંચાઈ = b
∴ લંબઘનનું કુલ પૃષ્ઠફળ
= 2 (લંબાઈ × પહોળાઈ + પહોળાઈ × ઊંચાઈ + ઊંચાઈ × લંબાઈ)
= 2 (2b × b + b × b + b × 2b)
= 2 (2b² + b² + 2b²)
= 2 (5b²) = 10b²
જુઓ લંબઘનનું પૃષ્ઠફળ 12b² નથી.

(ii) જ્યારે ત્રણ ઘનને એકબીજા સાથે બરોબર જોડવામાં આવે છે, ત્યારે નવો આકાર લંબઘન થશે.
જેની લંબાઈ = 3D, પહોળાઈ = b અને ઊંચાઈ = b
∴ લંબઘનનું કુલ પૃષ્ઠફળ
= 2 (લંબાઈ × પહોળાઈ + પહોળાઈ × ઊંચાઈ + ઊંચાઈ × લંબાઈ)
= 2 (3b × b + b × b + b × 3b)
= 2 (3b² + b² + 3b²) = 2 (7b²) = 14b²
જુઓ લંબઘનનું પૃષ્ઠફળ 18b² નથી.

2. સમાન બાજુવાળા 12 લંબઘનને કઈ રીતે ગોઠવીએ તો તેનાથી બનતા લંબઘનનું પૃષ્ઠફળ લઘુતમ થાય?
જવાબઃ
સમાન બાજુવાળા 12 લંબઘનને જુદી જુદી રીતે ગોઠવીને તેનાં પૃષ્ઠફળ શોધીએ : પરિસ્થિતિઃ 1

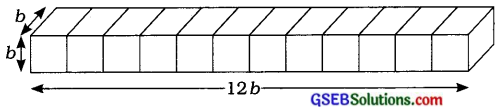
ઉપર પ્રમાણે ગોઠવણી કરીએ તો –
લંબાઈ = 12b, પહોળાઈ = b અને ઊંચાઈ = b
∴ લંબઘનનું કુલ પૃષ્ઠફળ
= 2 (લંબાઈ × પહોળાઈ + પહોળાઈ × ઊંચાઈ + ઊંચાઈ × લંબાઈ)
= 2 (12b × b + b × b + b × 12b)
= 2 (12b² + b² + 12b²)
= 2 (25b²)
= 50b²

પરિસ્થિતિ : 2

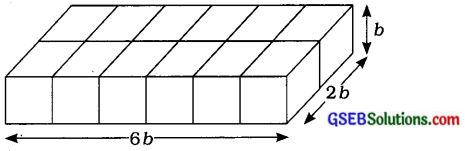
ઉપર પ્રમાણે ગોઠવણી કરીએ તો –
લંબાઈ = 6b, પહોળાઈ = 2b અને ઊંચાઈ = b
∴ લંબઘનનું કુલ પૃષ્ઠફળ
= 2 (લંબાઈ × પહોળાઈ + પહોળાઈ × ઊંચાઈ + ઊંચાઈ × લંબાઈ)
= 2 (6b × 2b + 2b × b + b × 6b)
= 2 (12b² + 2b² + 6b²)
= 2 (20b²)
= 40b²

પરિસ્થિતિ: 3

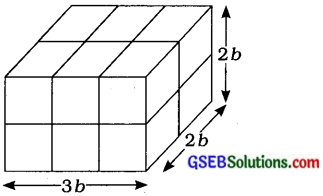
ઉપર પ્રમાણે ગોઠવણી કરીએ તો –
લંબાઈ = 3b, પહોળાઈ = 2b અને ઊંચાઈ = 2b
∴ લંબઘનનું કુલ પૃષ્ઠફળ
= 2 (લંબાઈ × પહોળાઈ + પહોળાઈ × ઊંચાઈ + ઊંચાઈ × લંબાઈ)
= 2 (3b × 2b + 2b × 2b + 2b × 3b)
= 2 (6b² + 4b² + 6b²)
= 2 (16b²)
= 32b²
ત્રણે પરિસ્થિતિ જોતાં જણાય છે કે 12 લંબઘનની ગોઠવણી પરિસ્થિતિ : 3 મુજબ ગોઠવણી કરતાં તેનું લઘુતમ પૃષ્ઠફળ થાય.

પ્રશ્ન 3.
આકૃતિમાં દર્શાવ્યા મુજબ એક ઘન ઉપર રંગ કર્યા બાદ તેના એકસરખા 64 ઘન બને તેમ કાપવામાં આવેલ છે અને અલગ કરવામાં આવે છે, તો આમાંથી કેટલા ઘન એવા હશે કે તેની એક પણ બાજુ રંગેલી નહીં હોય? કેટલા ઘનનું માત્ર એક ફલક (બાજુ) રંગેલું હશે? કેટલા ઘનની બે સપાટી રંગેલી હશે? અને કેટલા ઘનની ત્રણ સપાટી રંગવાળી હશે?

ઉત્તરઃ
રંગ કરેલા મોટા ઘનને કાપીને એકસરખા 64 ઘન બનાવતાં મળતા ઘન નીચે પ્રમાણે હોય:

1. 8 ઘન એવા હશે કે જેની એક પણ બાજુ (ફલક) રંગેલી નહીં હોય. (∵ બરાબર વચ્ચેના 4 × 2)
2. 24 ઘન એવા હશે કે જેની એક જ બાજુ (ફલક) રંગેલી હોય. (∵ દરેક ફલક પર 4 × 6)
3. 24 ઘન એવા હશે કે જેની બે બાજુ (ફલક) રંગેલી હોય. (∵ દરેક ફલક પર 4 × 6)
4. 8 ઘન એવા હશે કે જેની ત્રણ બાજુ (ફલક) રંગેલી હોય. (∵ દરેક ફલક પર 2 × 4)

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર 184)

1. આકૃતિમાં દર્શાવેલા નળાકારનું કુલ પૃષ્ઠફળ શોધોઃ

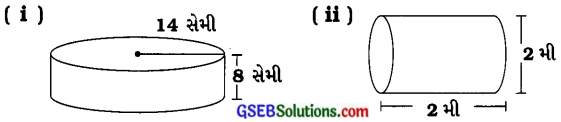
જવાબ:
(i) નળાકારની ત્રિજ્યા (r) = 14 સેમી અને નળાકારની ઊંચાઈ (h) = 8 સેમી
નળાકારનું કુલ પૃષ્ઠફળ = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 14 (14 + 8)
= 2 × 22 × 2 × 22
= 1936 સેમી²

(ii) નળાકારની ત્રિજ્યા (r) = વ્યાસ ÷ 2 = \(\frac {2}{2}\) = 1 મી અને ઊંચાઈ (h) = 2 મી
નળાકારનું કુલ પૃષ્ઠફળ = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 1 (1 + 2)
= 2 × \(\frac {22}{7}\) × 3
= \(\frac {132}{7}\) મી²
= 18\(\frac {6}{7}\)મી²

વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબર . 184)

1. નોંધ કરો કે કોઈ નળાકારના પાર્થ પૃષ્ઠફળ (વક્રસપાટીનું ક્ષેત્રફળ) નળાકારના આધારના પરિઘ × નળાકારની ઊંચાઈ જેટલું હોય છે. શું આપણે લંબઘનના પાર્થ પૃષ્ઠફળ (ચારે દીવાલનું ક્ષેત્રફળ)ને આધાર(તળિયા)ના લંબચોરસની પરિમિતિ × લંબઘનની ઊંચાઈના સ્વરૂપમાં લખી શકીએ?
જવાબ:

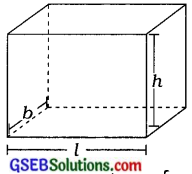
ધારો કે લંબઘનની લંબાઈ l, પહોળાઈ છે અને ઊંચાઈ h છે.
∴ લંબઘનનું પાર્શ્વ પૃષ્ઠફળ = લંબઘનની ચારે બાજુઓનાં ક્ષેત્રફળોનો સરવાળો
= (l × h) + (l × h) + (b × h) + (b × h)
= 2lh + 2bh
= 2 (1 + b) × h
= લંબચોરસની પરિમિતિ × લંબઘનની ઊંચાઈ
નળાકાર માટે પાર્થ પૃષ્ઠફળ = નળાકારના આધારના પરિઘ (પરિમિતિ) × નળાકારની ઊંચાઈ
આમ, વિધાન લખી શકાય છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 188)

1. નીચેની આકૃતિમાં દર્શાવેલા લંબઘનનું ઘનફળ શોધોઃ

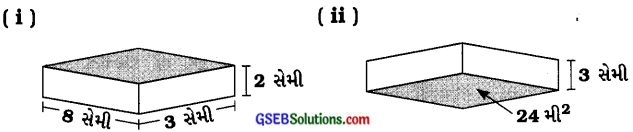
જવાબઃ
(i) લંબઘનની લંબાઈ (l) = 8 સેમી, પહોળાઈ (b) = 3 સેમી અને ઊંચાઈ (h) = 2 સેમી
લંબઘનનું ઘનફળ = પાયાનું ક્ષેત્રફળ × ઊંચાઈ
= (l × b) × h
= (8 × 3) × 2
= 24 × 2 = 48 સેમી³
અથવા:
લંબઘનનું ઘનફળ = l × b × h
= 8 × 3 × 2 = 48 સેમી³

(ii) લંબઘનનું પાયાનું ક્ષેત્રફળ = 24 મી² અને ઊંચાઈ (h)
= 3 સેમી = \(\frac {3}{100}\) મીટર
∴ લંબઘનનું ઘનફળ = પાયાનું ક્ષેત્રફળ × ઊંચાઈ
= 24 × \(\frac {3}{100}\) = 0.72 મી³

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર .189)

1. નીચે આપેલા ઘનના ઘનફળ શોધોઃ

પ્રશ્ન (a)
4 સેમી બાજુવાળો સમઘન
જવાબઃ
સમઘનની લંબાઈ (l) = 4 સેમી
∴ સમઘનનું ઘનફળ = l³ = 4 × 4 × 4 = 64 સેમી³

પ્રશ્ન (b)
1.5 મીટર બાજુવાળો સમઘન
જવાબઃ
સમઘનની લંબાઈ (l) = 1.5 મીટર
∴ સમઘનનું ઘનફળ = l³ = 1.5 × 1.5 × 1.5
= \(\frac{15}{10} \times \frac{15}{10} \times \frac{15}{10}=\frac{3375}{1000}\) = 3.375 મી³

વિચારો, ચર્ચા કરો અને લખો: (પાઠ્યપુસ્તક પાન નંબર . 189)

1. એક કંપની બિસ્કિટ વેચે છે. બિસ્કિટને પેક કરવા માટે લંબઘન આકારના ડબાનો ઉપયોગ કરવામાં આવે છે. ડબો A → 3 સેમી × 8 સેમી × 20 સેમી અને ડબો B → 4 સેમી × 12 સેમી × 10 સેમીનો છે, તો કંપનીને કયા માપના ડબાનો ઉપયોગ કરવાથી આર્થિક લાભ થશે? કેમ? શું તમે આવા કોઈ બીજા આકારના ડબાનો ઉપયોગ કરવાની સલાહ આપી શકો કે જેનું ઘનફળ તેના જેટલું જ હોય પરંતુ આર્થિક દૃષ્ટિએ વધુ લાભદાયક હોય.
જવાબઃ
ડબા A માટે:
ઘનફળ = l × b × h = 3 × 8 × 20 = 480 સેમી³
પૃષ્ઠફળ = 2 (lb + bh + nh) = 2 [(3 × 8) + (8 × 20) + (20 × 3)]
= 2 (24 + 160 + 60) = 2 (244) = 488 સેમી²

ડબા B માટે:
ઘનફળ = l × b × h = 4 × 12 × 10 = 480 સેમી³
પૃષ્ઠફળ = 2(lb + bh + lh) = 2 (4 × 12) + (12 × 10) + (10 × 4)].
= 2 (48 + 120 + 40) = 2 (208) = 416 સેમી²
ઉપરનાં પરિણામો જોતાં જણાય છે કે –
ડબા Aનું ઘનફળ અને ડબા Bનું ઘનફળ સરખું છે.
પરંતુ ડબા Bનું પૃષ્ઠફળ ઓછું છે. તેથી તેનો ઉપયોગ કરવાથી કંપનીને આર્થિક લાભ થાય.
અમારી દષ્ટિએ બીજા માપનો ડબો : 8 સેમી × 6 સેમી × 10 સેમી હોય, તો –
ઘનફળ = 8 × 6 × 10 = 480 સેમી³ જે ઉપરના બે ડબા જેટલું જ છે.
હવે, પૃષ્ઠફળ = 2 [(8 × 6) + (6 × 10) + (10 × 8)].
= 2 (48 + 60 + 80) = 2 (188) = 376 સેમી²
આ ડબાનું પૃષ્ઠફળ ડબા B કરતાં પણ ઓછું છે.
∴ આ ડબો કંપની માટે વધુ લાભદાયક છે.

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર . 189)

1. નીચે આપેલા નળાકારનાં ઘનફળ મેળવોઃ

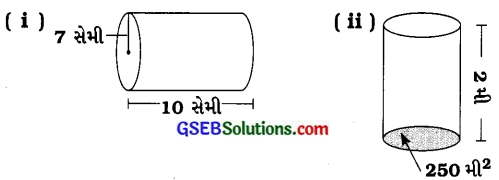
જવાબ:
(i) નળાકારની ત્રિજ્યા (r) = 7 સેમી અને નળાકારની ઊંચાઈ (h) = 10 સેમી
∴ નળાકારનું ઘનફળ = πr²h
= \(\frac {22}{7}\) × 7² × 10
= \(\frac {22}{7}\) × 7 × 7 × 10 = 1540 સેમી³

(ii) નળાકારના પાયાનું ક્ષેત્રફળ = 250 મી², ઊંચાઈ (h) = 2 મી.
∴ નળાકારનું ઘનફળ = પાયાનું ક્ષેત્રફળ × ઊંચાઈ
= 250 × 2 = 500 મી³