Gujarat Board GSEB Solutions Class 8 Maths Chapter 16 સંખ્યા સાથે રમત InText Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 16 સંખ્યા સાથે રમત InText Questions
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 250)
1. નીચે આપેલી સંખ્યાઓને તેમનાં વ્યાપક સ્વરૂપમાં લખો
પ્રશ્ન (i)
25
જવાબ:
25 = 10 × 2 + 5 [∵ ab = 10a + b].
![]()
પ્રશ્ન (ii)
73
જવાબ:
73 = 10 × 7 + 3 [∵ ab = 10a + b]
પ્રશ્ન (iii)
129
જવાબ:
129 = 100 × 1 + 2 × 10 + 9 [∵ abc = 100g + 10b + c]
પ્રશ્ન (iv)
302
જવાબ:
302 = 100 × 3 + 10 × 0 + 2 [∵ abc = 100a + 10b + c]
2. નીચે આપેલી સંખ્યાઓના સ્વરૂપને સામાન્ય સ્વરૂપમાં લખો:
પ્રશ્ન (i)
10 × 5 +6
જવાબ:
10 × 8 + 6 = 50 + 6 = 56
![]()
પ્રશ્ન (ii)
100 × 7 + 10 × 1 + 8
જવાબ:
100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718
પ્રશ્ન (iii)
100 × 9 + 10 × c + B
જવાબ:
100 × a + 10 × c + b = 100a + 10c + b = abc
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 251)
1. જો નીચે આપેલી સંખ્યા સુંદરમે ધારેલી હોય, તો પરિણામ શું મળશે તે ચકાસોઃ
પ્રશ્ન 1.
27
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 27
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 72
આ બંને સંખ્યાઓનો સરવાળો = 27 + 72 = 99
હવે, 99 = 11 (9) = 11 (2 + 7)
= 11 (ધારેલી સંખ્યાના અંકોનો સરવાળો)
![]()
પ્રશ્ન 2.
39
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 39
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 93
આ બંને સંખ્યાઓનો સરવાળો = 39 + 93 = 132
હવે, 132 = 11 (12) = 11 (3 + 9)
= 11 (ધારેલી સંખ્યાના અંકોનો સરવાળો)
પ્રશ્ન 3.
64
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 64
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 46
આ બંને સંખ્યાઓનો સરવાળો = 64 + 46 = 110
હવે, 110 = 11 (10) = 11 (6 + 4)
= 11 (ધારેલી સંખ્યાના અંકોનો સરવાળો)
પ્રશ્ન 4.
17
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 17
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 71
આ બંને સંખ્યાઓનો સરવાળો = 17 + 71 = 88
હવે, 88 = 11 (8) = 11 (1 + 7).
= 11 (ધારેલી સંખ્યાના અંકોનો સરવાળો)
(નોંધઃ ઉપરનાં પરિણામો પરથી સ્પષ્ટ છે કે બે અંકોની સંખ્યા અને તેના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યાનો સરવાળો 11નો ગુણક હોય છે એટલે કે સરવાળાને 11 વડે નિઃશેષ ભાગી શકાય છે.]
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 251)
જો સુંદરમે ધારેલ રકમ નીચે આપેલી સંખ્યામાંથી હોય, તો તેનું પરિણામ શું મળે તે ચકાસોઃ
પ્રશ્ન 1.
17
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 17
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 71
આ બંને સંખ્યાઓની બાદબાકી = 71 – 17 = 54
હવે, 54 = 9 × (6) = 9 × (7 – 1).
= 9 × (ધારેલી સંખ્યાના અંકોનો તફાવત)
પ્રશ્ન 2.
21
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 21
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 12
આ બંને સંખ્યાઓની બાદબાકી = 21 – 12 = 9
હવે, 9 = 9 × 1 = 9 × (2 – 1)
= 9 × (ધારેલી સંખ્યાના અંકોનો તફાવત)
પ્રશ્ન 3.
96
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 96
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 69
આ બંને સંખ્યાઓની બાદબાકી = 96 – 69 = 27
હવે, 27 = 9 × (3) = 9 × (9 – 6)
= 9 × (ધારેલી સંખ્યાના અંકોનો તફાવત)
![]()
પ્રશ્ન 4.
37
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 37.
આ સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 73
આ બંને સંખ્યાઓની બાદબાકી = 73 – 37 = 36
હવે, 36 = 9 × (4) = 9 × (7 – 3)
= 9 × (ધારેલી સંખ્યાના અંકોનો તફાવત)
[નોંધ: બે અંકોની સંખ્યા અને તેના અંકોનાં સ્થાન અદલબદલ કરવાથી મળતી સંખ્યાની બાદબાકી 9નો ગુણક હોય એટલે કે બાદબાકીને 9 વડે નિઃશેષ ભાગી શકાય છે.].
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 252)
જો મિનાક્ષીએ ધારેલી ત્રણ અંકોની સંખ્યાઓ નીચે મુજબની હોય, તો મળતાં પરિણામો જુઓઃ
પ્રશ્ન 1.
132
ઉત્તરઃ
મિનાક્ષીએ ધારેલી સંખ્યા = 132
એકમ અને સોના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 231
આ બે સંખ્યાઓનો તફાવત = 231 – 132 = 99
હવે, 99 ÷ 99 = 1 અને શેષ = 0
પ્રશ્ન 2.
469
ઉત્તરઃ
મિનાક્ષીએ ધારેલી સંખ્યા = 469
એકમ અને સોના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 964
આ બે સંખ્યાઓનો તફાવત = 964 – 469 = 495
હવે, 495 ÷ 99 = 5 અને શેષ = 0
![]()
પ્રશ્ન 3.
787
ઉત્તરઃ
મિનાક્ષીએ ધારેલી સંખ્યા = 737
એકમ અને સોના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 737
આ બે સંખ્યાઓનો તફાવત = 737 – 737 = 0
હવે, 0 ÷ 99 = 0 અને શેષ = 0.
પ્રશ્ન 4.
901
ઉત્તરઃ
મિનાક્ષીએ ધારેલી સંખ્યા = 901
એકમ અને સોના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી સંખ્યા = 109
આ બે સંખ્યાઓનો તફાવત = 901 – 109 = 792,
હવે, 792 ÷ 99 = 8 અને શેષ = 0
(નોંધઃ ત્રણ અંકોની સંખ્યા અને તેના એકમ તથા સોના અંકોનાં સ્થાન બદલતાં મળતી સંખ્યાનો તફાવત 99નો ગુણક હોય છે એટલે કે તફાવતને 99 વડે નિઃશેષ ભાગી શકાય છે.)
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર. 258)
જો સુંદરમે ધારેલ ત્રણ અંકોથી બનતી સંખ્યા નીચે મુજબ હોય, તો મળતાં પરિણામની ચકાસણી કરોઃ
પ્રશ્ન 1.
417
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 417
સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી બીજી બે સંખ્યાઓ 741 અને 174 છે.
આ ત્રણેય સંખ્યાઓનો સરવાળો = 417 + 741 + 174 = 1332
આ સરવાળાને 37 વડે ભાગતાં 1332 ÷ 37 = 36 અને શેષ = 0
![]()
પ્રશ્ન 2.
632
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 632
સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી બીજી બે સંખ્યાઓ 263 અને 326 છે.
આ ત્રણેય સંખ્યાઓનો સરવાળો = 632 + 263 + 326 = 1221
આ સરવાળાને 37 વડે ભાગતાં: 1221 ÷ 37 = 33 અને શેષ = 0
પ્રશ્ન 3.
117
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 117
સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી બીજી બે સંખ્યાઓ 711 અને 171 છે.
આ ત્રણેય સંખ્યાઓનો સરવાળો = 117 + 711 + 171 = 999
આ સરવાળાને 37 વડે ભાગતાં 999 ÷ 37 = 27 અને શેષ = 0
પ્રશ્ન 4.
937
ઉત્તરઃ
સુંદરમે ધારેલી સંખ્યા = 937
સંખ્યાના અંકોનાં સ્થાન અદલબદલ કરતાં મળતી બીજી બે સંખ્યાઓ 793 અને 379 છે.
આ ત્રણેય સંખ્યાઓનો સરવાળો = 937 + 793 + 379 = 2109
આ સરવાળાને 37 વડે ભાગતાં 2109 ÷ 37 = 57 અને શેષ = 0
(નોંધઃ ત્રણ અંકોની સંખ્યા અને તેમના ત્રણેય અંકોનાં સ્થાન અદલબદલ કરતાં મળતી બીજી બે સંખ્યાઓનો સરવાળો 37 વડે નિઃશેષ વિભાજ્ય હોય છે.]
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર. 257) (પ્રથમ ઉદાહરણ તમને ગણીને આપેલ છે.)
પ્રશ્ન 1.
જો N ÷ 5 માં શેષ ૩ વધે છે, તો જનો એકમનો અંક શું હોય? (જ્યારે કો એક સંખ્યાને 5 વડે ભાગીએ અને શેષ ૩ વધે, તો તે સંખ્યાનો એકમનો અંક 3 અથવા 8 હોય.)
ઉત્તરઃ
જો N ÷ 5માં શેષ 3 વધે છે, તો પનો એકમનો અંક 3 અથવા 8 હોય. દા. ત.,
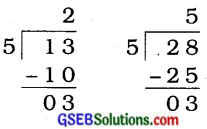
જુઓ: Nનો એકમનો અંક 3 અથવા 8 છે.
![]()
પ્રશ્ન 2.
જો N ÷ 5 માં શેષ 1 વધે છે, તો Nનો એકમનો અંક શું હોય?
ઉત્તરઃ
જો N ÷ 5માં શેષ 1 વધે છે, તો Nનો એકમનો અંક 1 અથવા 6 હોય. દા. ત,
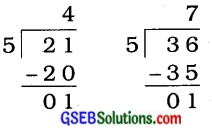
જુઓ : Nનો એકમનો અંક 1 અથવા 6 છે.
પ્રશ્ન 3.
જો N ÷ 5માં શેષ 4 વધે છે, તો જનો એકમનો અંક શું હોય?
ઉત્તરઃ
જો N ÷ 5માં શેષ 4 વધે છે, તો Nનો એકમનો અંક 9 અથવા 4 હોય. દા. ત,
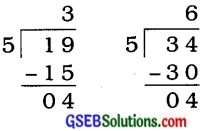
જુઓ : Nનો એકમનો અંક 9 અથવા 4 છે.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 257 – 258)
(પ્રથમ ઉદાહરણ ગણતરી સાથે આપેલ છે.)
પ્રશ્ન 1.
જો N ÷ 2માં શેષ 1 વધે છે, તો સંખ્યા જનો એકમનો અંક શું હશે? (N એ એકી સંખ્યા છે. તેથી તેનો એકમનો અંક 1, 3, 5, 7 કે 9 હશે.)
ઉત્તરઃ
જો Nને 2 વડે ભાગતાં શેષ 1 વધે છે, તો એનો એકમનો અંક એકી સંખ્યા હોય.
આમ, એનો એકમનો અંક 1, 3, 5, 7 કે 9 હોય. દા. ત.,
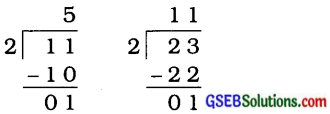
જુઓ : Nનો એકમનો અંક 1, 3, 5, 7 કે 9 છે.
![]()
પ્રશ્ન 2.
જો N ÷ 2 કરતાં શેષ શૂન્ય વધે છે, તો સંખ્યા જ્યનો એકમનો અંક શું હશે?
ઉત્તરઃ
જો Nને 2 વડે ભાગતાં શેષ 0 વધે છે, તો પનો એકમનો અંક બેકી સંખ્યા હોય.
આમ, નો એકમનો અંક 0, 2, 4, 6 કે 8 હોય. દા. ત.,
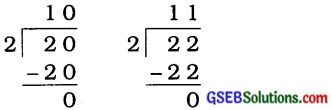
જુઓ: Nનો એકમનો અંક 0, 2, 4, 6 કે 8 હોય.
પ્રશ્ન 3.
ધારો કે સંખ્યા ૫, માટે N ÷ 5 કરતાં શેષ 4 મળે છે અને N ÷ 2 કરવાથી શેષ 1 મળે છે, તો સંખ્યા Nનો એકમનો અંક શું હશે?
ઉત્તરઃ
જો એને 5 વડે ભાગતાં શેષ 4 મળે છે.
∴ Nનો એકમનો અંક 4 અથવા 9 હોય.
હવે, આ જ સંખ્યાને 2 વડે ભાગતાં શેષ 1 મળે છે.
∴ N એકી સંખ્યા જ હોય.
∴ Nનો એકમનો અંક 9 જ હોય.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર. 259)
નીચેની સંખ્યાઓ 9 વડે વિભાજ્ય છે કે નહિ? તે ચકાસોઃ
પ્રશ્ન 1.
108
ઉત્તરઃ
108 સંખ્યાના અંકોનો સરવાળો = 1 + 0 + 8 = 9
હવે, 9 એ 9 વડે નિઃશેષ વિભાજ્ય છે. [∵ 9 ÷ 9 = 1 અને શેષ = 0]
∴ 108 એ 9 વડે નિઃશેષ વિભાજ્ય છે.
![]()
પ્રશ્ન 2.
616
ઉત્તરઃ
616 સંખ્યાના અંકોનો સરવાળો = 6 + 1 + 6 = 13
હવે, 13 એ 9 વડે નિઃશેષ ભાજ્ય નથી. [∵ 13 ÷ 9 = 1 અને શેષ = 4].
∴ 616 એ 9 વડે નિઃશેષ ભાજ્ય નથી.
પ્રશ્ન 3.
294
ઉત્તરઃ
294 સંખ્યાના અંકોનો સરવાળો = 2 + 9 + 4 = 15
હવે, 15 એ 9 વડે નિઃશેષ ભાજ્ય નથી. [∵ 15 ÷ 9 = 1 અને શેષ = 6]
∴ 294 એ 9 વડે નિઃશેષ ભાજ્ય નથી.
પ્રશ્ન 4.
432
ઉત્તરઃ
432 સંખ્યાના અંકોનો સરવાળો = 4 + 3 + 2 = 9
હવે, 9 એ 9 વડે નિઃશેષ વિભાજ્ય છે. [∵ 9 ÷ 9 = 1 અને શેષ = 0)
∴ 432 એ 9 વડે નિઃશેષ વિભાજ્ય છે.
પ્રશ્ન 5.
927
ઉત્તરઃ
927 સંખ્યાના અંકોનો સરવાળો = 9 + 2 + 7 = 18
હવે, 18 એ 9 વડે નિઃશેષ વિભાજ્ય છે. [∵ 18 ÷ 9 = 2 અને શેષ = 0].
∴ 927 એ 9 વડે નિઃશેષ વિભાજ્ય છે.
![]()
વિચારો, ચર્ચા કરો અને લખો: (પાઠ્યપુસ્તક પાન નંબર . 259)
પ્રશ્ન 1.
તમે જોયું કે 450 એ 10થી વિભાજ્ય છે. તે 2 અને 5થી પણ વિભાજ્ય છે. વળી, 2 અને 5 એ 10ના અવયવો પણ છે. તેવી જ રીતે 135 એ 9થી વિભાજ્ય છે. તે 3 થી પણ વિભાજ્ય છે. ઉપરાંત 3 એ 9નો અવયવ પણ છે. શું તમે એમ કહી શકો કે કોઈ સંખ્યા એ m થી વિભાજ્ય છે, તો તે સંખ્યા m ના અવયવોથી પણ વિભાજ્ય હોય?
ઉત્તરઃ
હા, આપેલી સંખ્યાને કોઈ જો m વડે નિઃશેષ ભાગી શકાય, તો તે સંખ્યાને m ના દરેક અવયવ વડે પણ નિઃશેષ ભાગી શકાય.
દા. ત., 12ને 6 વડે નિઃશેષ ભાગી શકાય છે.
6ના અવયવો 2 અને 3 છે.
આ 2 અને 3 વડે પણ 12ને નિઃશેષ ભાગી શકાય છે.
2.
પ્રશ્ન (i)
3 અંકોની સંખ્યા abc માટે
abc = 100d+ 10b + c
= 99a + 11b + (a – b + c).
= 11 (99 + 5) + (a – b + c)
ઉત્તરઃ
જો સંખ્યા વbc એ 11 વડે વિભાજ્ય હોય, તો (a – b + c) માટે શું કહી શકાય?
શું તે અનિવાર્ય છે કે (a + c – b) પણ 11 વડે નિઃશેષ ભાજ્ય હોય?
(a – b + c) એ 0 અથવા 11ની ગુણક હોય.
પ્રશ્ન (ii)
4 અંકોની સંખ્યા abcd માટે
abcd = 1000a + 100b + 10c + d
= 1001 + 99b + 11c – (a – b + c – d)
= 11 (91a + 9 + c) + [(b + d) – (a + c)]
ઉત્તરઃ
જો સંખ્યા abcd એ 11 વડે વિભાજ્ય હોય, તો [(b + d) – (a + c)]. માટે શું કહી શકાય?
[(b + d) – (a + c)] એ 0 અથવા 11ની ગુણક હોય.
![]()
પ્રશ્ન (iii)
ઉપર દર્શાવેલ કિસ્સાઓ (i) અને (ii) પરથી આપણે કહી શકીએ કે, કોઈ પણ સંખ્યા 11 વડે તો જ નિઃશેષ ભાગી શકાય જો તે સંખ્યાના એકી સ્થાન પર આવેલ સંખ્યાનો સરવાળો અને બેકી સ્થાન પર આવેલ અંકોના સરવાળાના તફાવતને 11 વડે નિઃશેષ ભાગી શકાય.
ઉત્તરઃ
હા, સંખ્યા 11 વડે ત્યારે જ નિઃશેષ વિભાજ્ય હોય જ્યારે સંખ્યાના જમણી બાજુથી એકી સ્થાન અને બેકી સ્થાનના અંકોના સરવાળાના તફાવતને 11 વડે નિઃશેષ ભાગી શકાય.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 260)
નીચેની સંખ્યાઓ માટે 3ની વિભાજ્યતા ચકાસોઃ
પ્રશ્ન 1.
108
ઉત્તરઃ
108 સંખ્યાના અંકોનો સરવાળો = 1 + 0 + 8 = 9.
હવે, 9 એ 3 વડે નિઃશેષ વિભાજ્ય છે. [∵ 9 ÷ 3 = 3 અને શેષ = 0]
∴ 108 એ 3 વડે નિઃશેષ વિભાજ્ય છે.
પ્રશ્ન 2.
616.
ઉત્તરઃ
616 સંખ્યાના અંકોનો સરવાળો = 6 + 1 + 6 = 13
હવે, 13 એ 3 વડે નિઃશેષ વિભાજ્ય નથી. [∵ 13 ÷ 3 = 4 અને શેષ = 1].
∴ 616 એ 3 વડે નિઃશેષ વિભાજ્ય નથી.
પ્રશ્ન 3.
294
ઉત્તરઃ
294 સંખ્યાના અંકોનો સરવાળો = 2 + 9 + 4 = 15
હવે, 15 એ 3 વડે નિઃશેષ વિભાજ્ય છે. [∵ 15 ÷ 3 = 5 અને શેષ = 0),
∴ 294 એ 3 વડે નિઃશેષ વિભાજ્ય છે.
![]()
પ્રશ્ન 4.
432
ઉત્તરઃ
432 સંખ્યાના અંકોનો સરવાળો = 4 + 3 + 2 = 9
હવે, 9 એ 3 વડે નિઃશેષ વિભાજ્ય છે. [∵ 9 ÷ 3 = 3 અને શેષ = 0)
∴ 432 એ 3 વડે નિઃશેષ વિભાજ્ય છે.
પ્રશ્ન 5.
927
ઉત્તરઃ
927 સંખ્યાના અંકોનો સરવાળો = 9 + 2 + 7 = 18
હવે, 18 એ 3 વડે નિઃશેષ વિભાજ્ય છે. [∵ 18 ÷ 3 = 6 અને શેષ = 0]
∴ 927 એ 3 વડે નિઃશેષ વિભાજ્ય છે.