Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 4 Practical Geometry Ex 4.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 4 Practical Geometry Ex 4.3
Question 1.
Construct the following quadrilaterals:
(i) Quadrilateral
MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
![]()
(ii) Quadrilateral
PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
(iii) Parallelogram
OKAY
HE = 5 cm
EA = 6 cm
∠R = 85°
![]()
(iv) Rectangle
HEAR
OK = 7 cm
KA = 5 cm
Solution:
(i) Steps of constructions:
I. Draw a Line segment MO = 6 cm
II. At M, draw \(\overrightarrow { MX } \) , such that ∠OMX = 60°
III. At O, draw \(\overrightarrow { OY } \) , such that ∠MOY = 105°
IV. From \(\overrightarrow { OY } \) , cut off OR = 4.5 cm
V. At R, draw \(\overrightarrow { RZ } \) , such that ∠ORZ = 105°
Let \(\overrightarrow { RZ } \) intersects \(\overrightarrow { MX } \) at E.
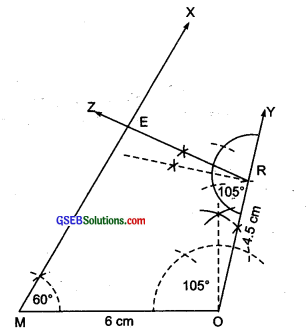
Thus, MORE is the required quadrilateral.
(ii) Steps of construction:
I. Draw a line segment AL = 6.5 cm.
II. At A, draw \(\overrightarrow { AX } \) such that ∠LAX = 110°
III. At L, draw \(\overrightarrow { LY } \) such that ∠ALY = 75°.
Note: ∠L = 75° is not given, but we can determine it using angle sum property
∵ Sum of three given angles
= 110° + 90° + 85° = 285°
∴ The fourth angle ∠L = 360° – 285° = 75°
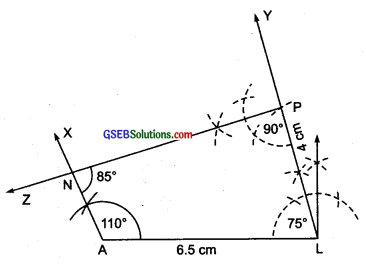
IV. rom \(\overrightarrow { LY } \) , cut-off LP = 4 cm.
V At P, draw \(\overrightarrow { PZ } \) such that ∠LPZ = 90°
Let \(\overrightarrow { PZ } \) and \(\overrightarrow { AX } \) intersect at N.
Thus, PLAN is the required quadrilateral.
![]()
(iii) Steps of construction:
I. Draw a line segment \(\overrightarrow { HE } \) = 5 cm.
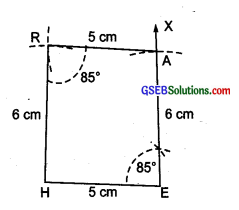
II. At E, draw \(\overrightarrow { EX } \) such that ∠HEA = 85°.
III. From \(\overrightarrow { EX } \) , cut-off EA = 6 cm.
IV. With centre at A and radius = 5 cm, draw an arc towards H.
V With centre at H and radius = 6 cm, draw an arc such that it intersects the previous arc at R.
VI. Join RA and RH.
Thus, HEAR is the required parallelogram
(iv) Steps of construction:
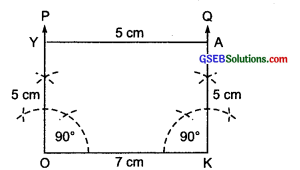
I. Draw a line segment Ok = 7 cm
II. draw \(\overrightarrow { OP } \) such that ∠KOP = 90°.
III. From \(\overrightarrow { OP } \) , cut-off \(\overrightarrow { OY } \) = 5 cm.
IV. At K, draw \(\overrightarrow { KQ } \) such that ∠OKQ = 90°.
V. From \(\overrightarrow { KQ } \) cut-off KA = 5 cm.
VI. Join A and Y.
Thus, OKAY is the required rectangle
![]()