GSEB Solutions Class 8 Maths Chapter 5 માહિતીનું નિયમન InText Questions

Gujarat Board GSEB Solutions Class 8 Maths Chapter 5 માહિતીનું નિયમન InText Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 5 માહિતીનું નિયમન InText Questions

પાઠ્યપુસ્તકમાંથી (પાન નંબર 69 – 70)

(1) ઉદાહરણ: નીચેનું દષ્ટાંત જુઓઃ

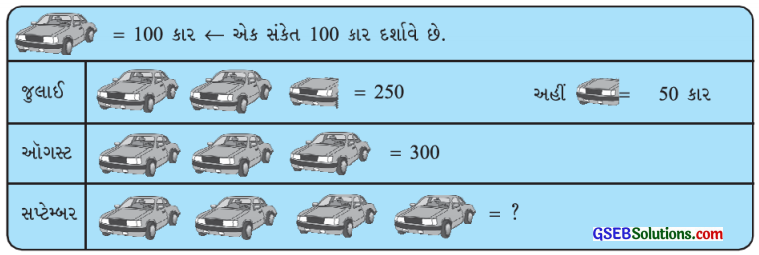
(i) જુલાઈ માસમાં કુલ કેટલી મોટરકારનું ઉત્પાદન થયું?
ઉત્તરઃ
જુલાઈ માસમાં કુલ 250 મોટરકારનું ઉત્પાદન થયું છે.

(ii) કયા માસમાં સૌથી વધુ મોટરકારનું ઉત્પાદન થયું?
ઉત્તરઃ
સપ્ટેમ્બર માસમાં સૌથી વધુ મોટરકારનું ઉત્પાદન થયું છે.

(2) ઉદાહરણઃ

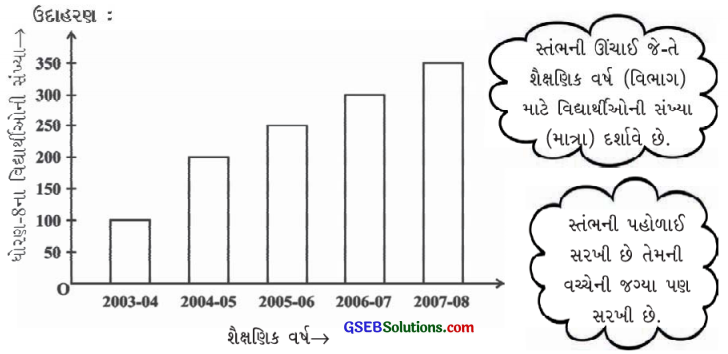
(i) લંબ આલેખ દ્વારા કઈ માહિતી દર્શાવવામાં આવી છે?
ઉત્તરઃ
ઉપરનો લંબ આલેખ જુદાં જુદાં શૈક્ષણિક વર્ષોમાં ધોરણ 8ના વિદ્યાર્થી ઓની સંખ્યા દર્શાવે છે.

(ii) કયા વર્ષમાં વિદ્યાર્થીઓની સંખ્યામાં વધારો સૌથી મહત્તમ છે?
ઉત્તરઃ
વર્ષ 2004-05માં વિદ્યાર્થીઓની સંખ્યામાં વધારો સૌથી મહત્તમ છે.

(iii) કયા વર્ષમાં વિદ્યાર્થીઓની સંખ્યા સૌથી વધુ છે?
ઉત્તરઃ
વર્ષ 2007-2008માં વિદ્યાર્થીઓની સંખ્યા સૌથી વધુ છે.

(iv) નીચેનું વિધાન ખરું છે કે ખોટું?
વર્ષ 2005-06ના વિદ્યાર્થીઓની સંખ્યા વર્ષ 2003-04 કરતાં બમણી છે.”
ઉત્તરઃ
ખોટું, કારણ કે વર્ષ 2005-06માં વિદ્યાર્થીઓની સંખ્યા વર્ષ 2003-04 કરતાં બમણી નહીં પણ બમણાથી પણ વધારે છે.

(3) ઉદાહરણ :

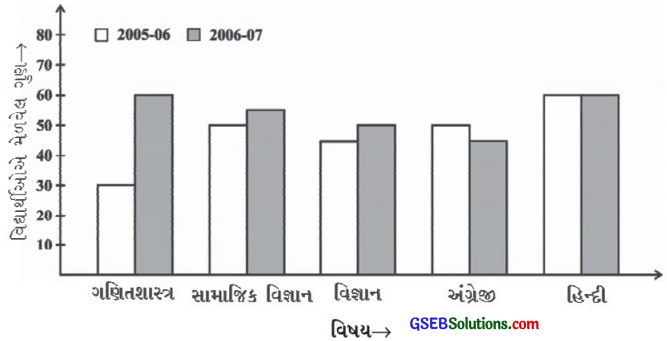
(i) દ્વિ-લંબ આલેખ દ્વારા કઈ માહિતી દર્શાવવામાં આવી છે?
ઉત્તરઃ
દ્વિ-લંબ આલેખ દ્વારા વર્ષ 2005 – 06 અને વર્ષ 2006-07માં જુદા જુદા વિષયોમાં વિદ્યાર્થીઓએ મેળવેલા ગુણ તથા ગુણની સરખા મણી દર્શાવવામાં આવી છે.

(ii) કયા વિષયના દેખાવમાં સૌથી વધુ વધારો થયો છે?
ઉત્તરઃ
ગણિતના વિષયમાં વિદ્યાર્થીઓના દેખાવમાં સૌથી વધુ વધારો થયો છે.

(iii) કયા વિષયના દેખાવમાં સૌથી વધુ ઘટાડો થયો છે?
ઉત્તરઃ
અંગ્રેજીના વિષયમાં વિદ્યાર્થીઓના દેખાવમાં સૌથી વધુ ઘટાડો થયો છે.

(iv) કયા વિષયમાં દેખાવ સમાન છે?
ઉત્તરઃ
હિન્દીના વિષયમાં દેખાવ સમાન છે.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 71)

જો લંબ આલેખના કોઈ સ્તંભની સ્થિતિમાં ફેરફાર કરવામાં આવે, તો શું આપેલી માહિતીનું અર્થઘટન બદલાય છે? શા માટે?
ઉત્તરઃ
લંબ આલેખના કોઈ સ્તંભની ઊંચાઈમાં ફેરફાર ન કરીએ અને માત્ર સ્થાનમાં જ ફેરફાર કરીએ તો માહિતીના અર્થઘટનમાં કોઈ જ બદલાવ થતો નથી.
કારણ: સ્તંભની ઊંચાઈ બદલાય તો જ માહિતીનું અર્થઘટન બદલાય.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 71)

નિચેની માહિતી દર્શાવતા યોગ્ય આલેખ દોરોઃ

1.

ઉત્તરઃ
ઉપરની માહિતી રજૂ કરવા માટે આપણે લંબ આલેખ દોરીશું. લંબ આલેખ માટે પરસ્પર લંબ બે અક્ષ \(\overleftrightarrow{\mathrm{OX}}\) અને \(\overleftrightarrow{\mathrm{OY}}\) દોરીશું. \(\overleftrightarrow{\mathrm{OX}}\) અક્ષ ઉપર મહિનાઓ અને \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ ઉપર વેચાયેલી ઘડિયાળની સંખ્યા દર્શાવીશું. \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ માટે અનુકૂળ પ્રમાણમાપ લઈશું. \(\overleftrightarrow{\mathrm{OX}}\) અક્ષ ઉપરના સ્તંભો સરખા અંતરે દોરતા જઈશું. વેચાયેલી ઘડિયાળની સંખ્યાના પ્રમાણમાં જે-તે માસનો સ્તંભ પ્રમાણમાપ પ્રમાણેની ઊંચાઈનો દોરીશું.

જુઓઃ 500 ઘડિયાળ = 1 સેમી પ્રમાણમાપ લીધું છે.
∴ 1000 ઘડિયાળ માટે 2 સેમી, 1500 ઘડિયાળ માટે 3 સેમી, 2000 ઘડિયાળ માટે 4 સેમી અને 2500 ઘડિયાળ માટે 5 સેમી ઊંચાઈના સ્તંભ થશે.

આમ, લંબ આલેખ નીચે પ્રમાણે તૈયાર થાય :

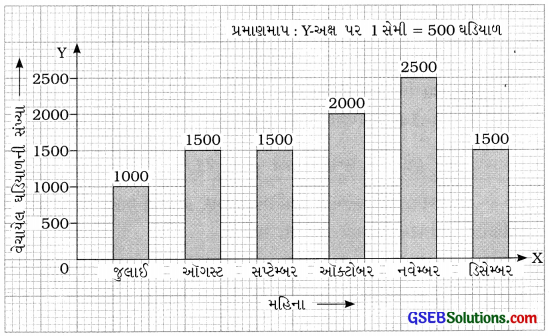
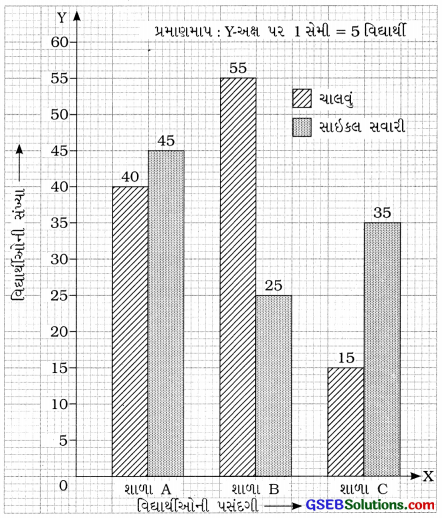
2.

વિદ્યાર્થીની પસંદગી	શાળા A	શાળા B	શાળા C
ચાલવું (Walking)	40	55	15
સાઇકલ સવારી (Cycling)	45	25	35

અહીં વિદ્યાર્થીઓની બે પસંદગીની સરખામણી આપી છે. સરખામણી દર્શાવવા માટે આપણે દ્વિ-લંબ આલેખ દોરીશું. પરસ્પર લંબ \(\overleftrightarrow{\mathrm{OX}}\) અને \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ દોરીશું. \(\overleftrightarrow{\mathrm{OX}}\) અક્ષ ઉપર વિદ્યાર્થીઓની પસંદગી અને \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ ઉપર વિદ્યાર્થીઓની સંખ્યા દર્શાવીએ. આ માટે \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ ઉપર અનુકૂળ પ્રમાણમાપ: 1 સેમી = 5 વિદ્યાર્થીઓ લઈશું.

આમ, દ્વિ-લંબ આલેખ નીચે પ્રમાણે તૈયાર થાય :

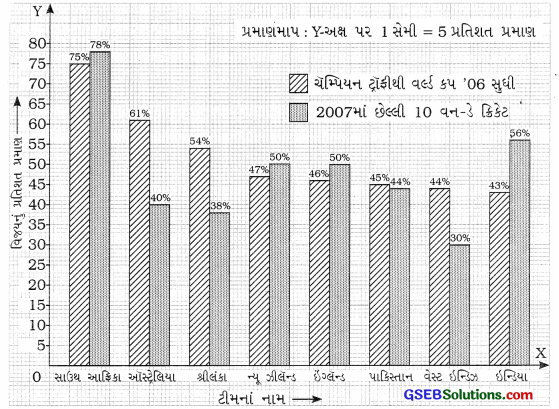
3. વન-ડે ક્રિકેટમાં વિશ્વની શ્રેષ્ઠ 8 ક્રિકેટ ટીમના વિજયનું પ્રતિશત પ્રમાણ:

ટીમ	ચૅમ્પિયન ટ્રૉફીથી વર્લ્ડ કપ ’06 સુધી	2007માં છેલ્લી 10 વન-ડે ક્રિકેટ
સાઉથ આફ્રિકા	75%	78%
ઑસ્ટ્રેલિયા	61%	40%
શ્રીલંકા	54%	38%
ન્યૂ ઝીલૅન્ડ	47%	50%
ઇંગ્લેન્ડ	46%	50%
પાકિસ્તાન	45%	44%
વેસ્ટ ઇન્ડિઝ	44%	30%
ઇન્ડિયા	43%	56%

ઉત્તરઃ
અહીં વન-ડે ક્રિકેટમાં વિશ્વની શ્રેષ્ઠ 8 ક્રિકેટ ટીમના વિજયનું પ્રતિશત પ્રમાણ આપેલ છે. માહિતીની સરખામણી કરવાની હોવાથી આપણે દ્વિ-લંબ આલેખની રચના કરીશું. આલેખમાં પરસ્પર લંબ બે અક્ષ \(\overleftrightarrow{\mathrm{OX}}\) અને \(\overleftrightarrow{\mathrm{OY}}\) દોરીશું. \(\overleftrightarrow{\mathrm{OX}}\) અક્ષ ઉપર ટીમોનાં નામ દર્શાવીશું અને \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ ઉપર વિજયનું પ્રતિશત પ્રમાણ દર્શાવીશું. \(\overleftrightarrow{\mathrm{OY}}\) અક્ષ માટે પ્રમાણમાપ 1 સેમી = 5 પ્રતિશત પ્રમાણ દર્શાવીશું. આમ, દ્વિ-લંબ આલેખ નીચે પ્રમાણે તૈયાર થાય :

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 72)

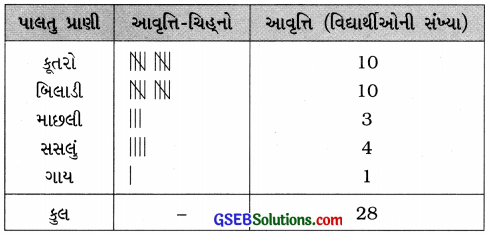
1. વિદ્યાર્થીઓના એક સમૂહને પાલતું પ્રાણીઓમાં સૌથી વધુ ગમતાં પ્રાણી વિશે પૂછવામાં આવ્યું. જેનું પરિણામ નીચે મુજબ છે :
કૂતરો, બિલાડી, બિલાડી, માછલી, બિલાડી, સસલું, કૂતરો, બિલાડી, સસલું, કૂતરો, બિલાડી, કૂતરો, કૂતરો, કૂતરો, બિલાડી, ગાય, માછલી, સસલું, કૂતરો, બિલાડી, કૂતરો, બિલાડી, બિલાડી, કૂતરો, સસલું, બિલાડી, માછલી, કૂતરો.
આ માહિતી પરથી આવૃત્તિ-વિતરણ કોષ્ટક તૈયાર કરો.
ઉત્તરઃ
માગ્યા પ્રમાણેનું આવૃત્તિ-ચિહ્નો દર્શાવતું આવૃત્તિ-વિતરણ કોષ્ટક નીચે પ્રમાણે તૈયાર થાય :

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 73-74)

1. નીચે આપેલ આવૃત્તિ-વિતરણ કોષ્ટકનો અભ્યાસ કરો અને નીચેના પ્રશ્નોના જવાબ આપોઃ
એક કારખાનાનાં 550 કામદારોનું દૈનિક વેતન દર્શાવતું આવૃત્તિ-વિતરણ કોષ્ટક નીચે મુજબ છે :

વર્ગ અંતરાલ (દૈનિક આવક રૂપિયામાં)	આવૃત્તિ (કામદારની સંખ્યા)
100 – 125	45
125 – 150	25
150 – 175	55
175 – 200	125
200 – 225	140
225 – 250	55
250 – 275	35
275 – 300	50
300 – 325	20
કુલ	550

(i) અહીં વર્ગલંબાઈ કેટલી છે?
ઉત્તરઃ
આવૃત્તિ-વિતરણ કોષ્ટકમાં વર્ગલંબાઈ 25 છે. જુઓ (125 – 100 = 25)

(ii) કયા વર્ગની આવૃત્તિ સૌથી વધુ છે?
ઉત્તરઃ
વર્ગ 200 – 225ની આવૃત્તિ સૌથી વધુ છે. (જુઓ આવૃત્તિ 140 જે સૌથી વધુ આવૃત્તિ છે.)

(iii) કયા વર્ગની આવૃત્તિ સૌથી ઓછી છે?
ઉત્તરઃ
વર્ગ 300 – 325ની આવૃત્તિ સૌથી ઓછી છે. (જુઓ આવૃત્તિ 20 જે સૌથી ઓછી આવૃત્તિ છે.)

(iv) વર્ગ અંતરાલ 250 – 275ની ઊર્ધ્વસીમા શું છે?
ઉત્તરઃ
વર્ગ 250 – 275ની ઊર્ધ્વસીમા 275 છે.

(v) કયા બે વર્ગમાં સમાન આવૃત્તિ છે?
ઉત્તરઃ
વર્ગ 150 – 175. અને વર્ગ 225 – 250માં સમાન આવૃત્તિ છે.
(જુઓ બંને વર્ગની આવૃત્તિ 55 છે.)

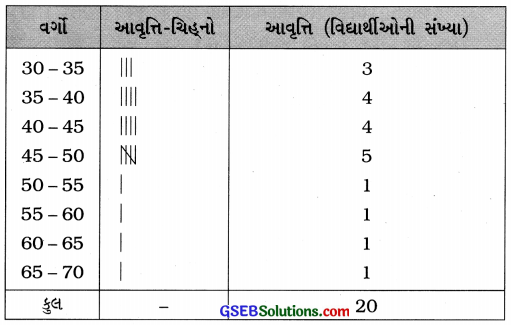
2. એક વર્ગના 20 વિદ્યાર્થીઓનાં વજન (કિગ્રામાં) દર્શાવતી નીચેની માહિતી માટે એવું આવૃત્તિ-વિતરણ કોષ્ટક તૈયાર કરો જેના વર્ગો 30-35, 35-40 અને એ રીતે આગળ .. હોય.
40, 38, 33, 48, 60, 53, 31, 46, 34, 36, 49, 41, 55, 49, 65, 42, 44, 47, 38, 39
ઉત્તરઃ
સૌથી નાનું અવલોકન = 31 અને સૌથી મોટું અવલોકન = 65
વગોં : 30 – 35, 35 – 40, 40 – 45, … લેવાના છે.

આમ, આવૃત્તિ-વિતરણ કોષ્ટક નીચે પ્રમાણે તૈયાર થાય :

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 75 – 76)

1. નીચેના સ્તંભલેખનું અવલોકન કરો અને નીચેના પ્રશ્નોના જવાબ આપો?

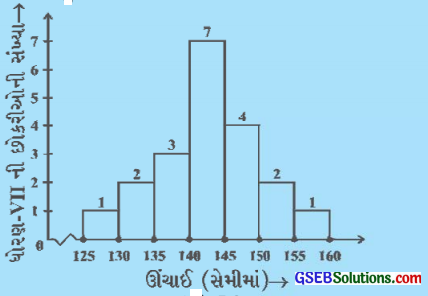
(i) ઉપરોક્ત સ્તંભાલેખમાં શું માહિતી આપવામાં આવી છે?
ઉત્તરઃ
આ ખંભાલેખમાં ધોરણ VIIની છોકરીઓની ઊંચાઈ(સેમીમાં)ની માહિતી આપવામાં આવી છે.

(ii) કયા વર્ગમાં છોકરીઓની સંખ્યા મહત્તમ છે?
ઉત્તરઃ
140 – 145 વર્ગમાં છોકરીઓની સંખ્યા મહત્તમ છે.
(જુઓ આ સંખ્યા 7 છે.)

(iii) કેટલી છોકરીઓની ઊંચાઈ 145 સેમી કે તેથી વધારે છે?
ઉત્તરઃ
145 સેમી કે તેથી વધુ ઊંચાઈ ધરાવતી છોકરીઓ = 4 + 2 + 1 = 7

(iv) જો આપણે છોકરીઓને નીચે મુજબ ત્રણ વિભાગમાં વહેંચણી કરીએ, તો દરેક વિભાગની સંખ્યા શું થાય?
150 સેમી કે તેથી વધુ – જૂથ A
140 સેમી અને 150 સેમીની વચ્ચે – જૂથ B
150 સેમીથી ઓછી – જૂથ C
ઉત્તરઃ
જૂથ A : 150 સેમી કે તેથી વધુ ઊંચાઈ = 2 + 1 = 3 છોકરીઓ
જૂથ B : 140 સેમી અને 150 સેમીની વચ્ચે ઊંચાઈ = 7 + 4 = 11 છોકરીઓ
જૂથ C : 150 સેમીથી ઓછી ઊંચાઈ = 4 + 7 + 3 + 2 + 1 = 17 છોકરીઓ

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 78)

1. નીચે દર્શાવેલ દરેક પાઈ-આલેખ એક વર્ગની વિવિધ માહિતી દર્શાવે છે. આ દરેક માહિતી વર્તુળનો કેટલામો ભાગ દર્શાવે છે તે શોધોઃ

ઉત્તરઃ
(i) ‘છોકરીઓ અથવા છોકરાઓનો’ પાઈ-આલેખઃ
‘છોકરીઓ’ દર્શાવતો વર્તુળનો ભાગ = 50 % = \(\frac {50}{100}\) = \(\frac {1}{2}\)
‘છોકરાઓ’ દર્શાવતો વર્તુળનો ભાગ = 50 % = \(\frac {50}{100}\) = \(\frac {1}{2}\)

(ii) ‘શાળા પરિવહન’નો પાઈ-આલેખઃ
‘પગપાળા’ દર્શાવતો વર્તુળનો ભાગ = 40 % = \(\frac {40}{100}\) = \(\frac {2}{5}\)
બસ અથવા કાર દર્શાવતો વર્તુળનો ભાગ = 40 % = \(\frac {40}{100}\) = \(\frac {2}{5}\)
‘સાઇકલ’ દર્શાવતો વર્તુળનો ભાગ = 20 % = \(\frac {20}{100}\) = \(\frac {1}{5}\)

(iii) ‘ભાવાવરણ’નો પાઈ-આલેખ:
‘ધિક્કાર’ દર્શાવતો વર્તુળનો ભાગ = 15 % = \(\frac {15}{100}\) = \(\frac {3}{20}\)
‘પ્રેમ’ દર્શાવતો વર્તુળનો ભાગ = (100 – 15) % = 85 % = \(\frac {85}{100}\) = \(\frac {17}{20}\)

2. આકૃતિમાં દર્શાવેલ પાઈ-ચાર્ટ પરથી નીચેના પ્રશ્નોના જવાબ આપો?

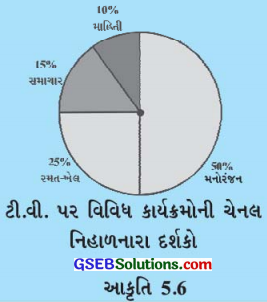
ઉત્તરઃ
આપેલા પાઈ-ચાર્ટ પરથી નીચે પ્રમાણેનું માહિતી કોષ્ટક મળે છે :

દર્શકો	ટકા
રમત-ખેલ જોનાર	25%
સમાચાર જોનાર	15%
માહિતી જોનાર	10%
પર્યાવરણ જોનારા	50%

(i) કયા પ્રકારના કાર્યક્રમો સૌથી વધુ જોવાય છે?
ઉત્તરઃ
પર્યાવરણનો કાર્યક્રમ સૌથી વધુ જોવાય છે.

(ii) કયા બે પ્રકારના કાર્યક્રમો નિહાળનાર દર્શકોની સંખ્યા રમત વિભાગના કાર્યક્રમો નિહાળનાર દર્શકોની સંખ્યા બરાબર છે?
ઉત્તરઃ
સમાચાર અને માહિતી કાર્યક્રમ નિહાળનાર દર્શકોની કુલ સંખ્યા એટલે કે 15 % + 10 % = 25 % એ રમત-ખેલ નિહાળનાર દર્શકોની કુલ સંખ્યા 25 %ની બરાબર છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 81)

નીચેની માહિતી માટે પાઈ-ચાર્ટ બનાવો :

દિવસ દરમિયાન બાળક દ્વારા પસાર કરાતો સમય.
ઊંઘ – 8 કલાક
શાળા – 6 કલાક
ગૃહકાર્ય – 4 કલાક
રમત – 4 કલાક
અન્ય – 2 કલાક
ઉત્તરઃ
પાઈ-ચાર્ટ દોરતાં પહેલાં પ્રત્યેક વિગત માટે વર્તુળની બે ત્રિજ્યાઓ વચ્ચે કેટલા અંશનો ખૂણો બનાવવો પડે તે માહિતી શોધવી પડે.

પ્રવૃત્તિ	દિવસના 24 કલાકમાં પ્રવૃત્તિનો ગાળો	પ્રવૃત્તિને સંગત બનતો ખૂણો
ઊંધ	8 કલાક	\(\frac {8}{24}\) × 360° = 120°
શાળા	6 કલાક	\(\frac {6}{24}\) × 360° = 90°
ગૃહકાર્ય	4 કલાક	\(\frac {4}{24}\) × 360° = 60°
રમત	4 કલાક	\(\frac {4}{24}\) × 360° = 60°
અન્ય	2 કલાક	\(\frac {2}{24}\) × 360° = 30°

ઉપરની માહિતી પરથી પાઈ-ચાર્ટ આલેખ નીચે પ્રમાણે તૈયાર થાય :

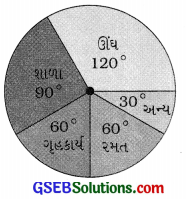
નોંધઃ ઊંઘની પ્રવૃત્તિ માટે – એવી બે ત્રિજ્યાઓ દોરો જેમની વચ્ચેનો કેન્દ્ર આગળના ખૂણાનું કેન્દ્રીય ખૂણો) માપ 120° હોય.
આ રીતે બહારની બધી પ્રવૃત્તિ માટે ત્રિજ્યાઓ દોરતાં પાઈ-ચાર્ટ તૈયાર થાય. આ ખૂણા દોરવા કોણમાપકનો ઉપયોગ કરવામાં આવે છે.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 81)

નીચેની માહિતી દર્શાવવા કયા પ્રકારનો આલેખ દોરવો વધુ યોગ્ય છે?

પ્રશ્ન 1.
રાજ્યનું ખાદ્ય અનાજનું ઉત્પાદન

ઉત્તરઃ
ઉપરની માહિતી માટેની યથાયોગ્ય રજૂઆત એ લંબ આલેખ છે.

પ્રશ્ન 2.
લોકોની ખોરાક માટેની પસંદગી

પસંદગીનો ખોરાક	લોકોની સંખ્યા
ઉત્તર ભારત	30
દક્ષિણ ભારત	40
ગુજરાતી	25
અન્ય	25
કુલ	120

ઉત્તરઃ
ઉપરની માહિતી માટેની યથાયોગ્ય રજૂઆત એ પાઈ-ચાર્ટ છે.

પ્રશ્ન 3.
કારખાનાના કામદારોની દૈનિક આવક
ઉત્તરઃ

દૈનિક આવક (₹)	કામદારોની સંખ્યા
75 – 100	45
100 – 125	35
125 – 150	55
150 – 175	30
175 – 200	50
200 – 225	125
225 – 250	140
કુલ	480

ઉપરની માહિતી માટેની યથાયોગ્ય રજૂઆત સ્તંભ-આલેખ છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 83-84)

પ્રશ્ન 1.
તમે કોઈ સ્કૂટર શરૂ કરવા જઈ રહ્યા છો, તો તેની સંભવિત શક્યતાઓ શું હોઈ શકે?
ઉત્તરઃ

• સ્કૂટર ચાલુ થાય.
• સ્કૂટર ચાલુ ન પણ થાય.

પ્રશ્ન 2.
જ્યારે આપણે એક પાસો (Die) ફેકીએ છીએ ત્યારે કઈ છ સંભવિત શક્યતાઓ રહેલી હોય છે?
ઉત્તરઃ
જ્યારે આપણે એક પાસો (Die) ફેકીએ છીએ ત્યારે નીચે પ્રમાણે છ સંભવિત શક્યતાઓ રહેલી હોય છે :

• પાસાની ઉપર 1 આવે
• પાસાની ઉપર 2 આવે
• પાસાની ઉપર 3 આવે
• પાસાની ઉપર 4 આવે
• પાસાની ઉપર 5 આવે
• પાસાની ઉપર 6 આવે

પ્રશ્ન 3.
આકૃતિમાં દર્શાવ્યા મુજબનું એક ચક્ર જ્યારે તમે ઘુમાવો છો ત્યારે શું શક્યતાઓ રહેલી છે? (યાદી કરો.) (અહીં શક્યતાઓ એટલે જ્યારે ચક્ર ઊભું રહે ત્યારે દર્શક-કાંટો કયા વૃત્તાંશ ઉપર આવશે તે.)

ઉત્તરઃ
ચક્રને ઘુમાવ્યા પછી ચક્ર ફરતું બંધ થતાં શક્ય પરિણામો નીચે પ્રમાણે છે :

• દર્શક-કાંટો A પર ઊભો રહે
• દર્શક-કાંટો B પર ઊભો રહે
• દર્શક-કાંટો C પર ઊભો રહે

પ્રશ્ન 4.
તમારી પાસે આકૃતિમાં દર્શાવ્યા મુજબના એક ઘડામાં વિવિધ રંગોવાળા પાંચ દડાઓ રાખેલા છે. તમારે તેમાં જોયા વગર કોઈ એક દડો પસંદ કરવાનો છે. તમને કયા રંગનો દડો મળશે તેની પ્રયત્નોની યાદી બનાવો.

ઉત્તરઃ
મળતાં પરિણામો નીચે પ્રમાણે છે :

• દડો જ મળે
• દડો R મળે
• દડો B મળે
• દડો G મળે
• દડો Y મળે

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 84)

પાસો (Die) ઉછાળવાની રમતમાં,

પ્રશ્ન 1.
શું પહેલા પાસો ફેંકનાર ખેલાડીને 6 મળવાની તકો વધુ રહે છે?
ઉત્તરઃ
ના, આવું કંઈ ન હોય.

પ્રશ્ન 2.
શું પ્રથમ ખેલાડી બાદ રમનાર બીજા ખેલાડીને 6 મળવાની તકો ઓછી રહે છે?
ઉત્તરઃ
ના, આવું કંઈ ન હોય.

પ્રશ્ન 3.
ધારો કે બીજા ખેલાડીને 6 મળે છે, તો તેનો એવો અર્થ કરી શકાય કે ત્રીજા ખેલાડીને 6 મળવાની કોઈ શક્યતા નથી?
ઉત્તરઃ
ના, આવું કંઈ ન હોય.

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબ 86)

1. ધારો કે તમે એક ચક્ર ઘુમાવો છો.

પ્રશ્ન (i).
આકૃતિમાં દર્શાવ્યા મુજબ, લીલા રંગનું વૃત્તાંશ હોય તેવી શક્યતાની યાદી કરો અને લીલા રંગનું વૃત્તાંશ ન હોય તેવી શક્યતાની યાદી કરો.

ઉત્તરઃ
લીલા રંગનું વૃત્તાંશ મળવાનાં શક્ય પરિણામો = 5
લીલા રંગનું વૃત્તાશ ન મળવાનાં પરિણામો = 3

પ્રશ્ન (ii).
લીલા રંગનું વૃત્તાંશ મળે તેની સંભાવના શોધો.
ઉત્તરઃ
ચક્રના સરખા કુલ ભાગ = 8 ∴ કુલ પરિણામો = 8
લીલા રંગનું વૃત્તાંશ મળવાનાં શક્ય પરિણામો = 5
∴ લીલા રંગનું વૃત્તાંશ મળવાની સંભાવના = \(\frac {5}{8}\)

પ્રશ્ન (iii).
લીલા રંગનું વૃત્તાશ ન મળે તેની સંભાવના શોધો.
ઉત્તરઃ
લીલા રંગ સિવાયનાં વૃત્તાંશ = 3
લીલા રંગનું વૃત્તાંશ ન મળવાની સંભાવના = \(\frac {3}{8}\)