Gujarat Board GSEB Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ Ex 6.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ Ex 6.2
1. નીચે આપેલી સંખ્યાઓના વર્ગ શોધોઃ
અહીં બધા દાખલામાં (a + b)2 = a2 + 2ab + b2 સૂત્રનો ઉપયોગ કરીશું:
પ્રશ્ન (i).
32
ઉત્તરઃ
(32)2 = (30 + 2)2
= 302 + 2 (30) (2) + (2)2
= 900 + 120 + 4
= 1024
પ્રશ્ન (ii).
35
ઉત્તરઃ
(35)2 = (30 + 5)
= (30) + 2 (30) (5) + (5)2
= 900 + 300 + 25
= 1200 + 25
= 1225
પ્રશ્ન (iii).
86
ઉત્તરઃ
(86)2 = (80 + 6)2
= (80)2 + 2 (80) (6) + (6)2
= 6400 + 960 + 36
= 7396
![]()
પ્રશ્ન (iv).
93
ઉત્તરઃ
(93)2 = (90 + 3)2
= (90)2 + 2 (90) (3) + (3)2
= 8100 + 540 + 9
= 8849
પ્રશ્ન (v).
71
ઉત્તરઃ
(71)2 = (70 + 1)2
= (70)2 + 2 (70) (1) + (1)2
= 4900 + 140 + 1
= 5041
પ્રશ્ન (vi).
46
ઉત્તરઃ
(46)2 = (40 + 6)2
= (40)2 + 2 (40) (6) + (6)2
= 1600 + 480 + 36
= 2116
આ રીતે પણ વર્ગ મેળવાય : (જેનો એકમનો અંક 5 હોય તેને જ લાગુ પડે.)
(ii) (35)2 = 3 × (૩ + 1) × 100 + 25
= 3 × (4) × 100 + 25
= 1200 + 25
= 1225
![]()
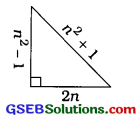
2. નીચે આપેલી સંખ્યા ધરાવતી પાયથાગોરીઅન ત્રિપુટી લખો:
પ્રશ્ન (i).
6
ઉત્તરઃ
અહીં 2n = 6
∴ n = 3
હવે, n2 – 1 = 32 – 1
= 9 – 1
= 8
અને n2 + 1 = 32 + 1
= 9 + 1
= 10
આમ, માગેલી પાયથાગોરીઅન ત્રિપુટી 6, 8, 10 છે.
પ્રશ્ન (ii).
14
ઉત્તરઃ
2n = 14
∴ n = 7
હવે, n2 – 1
= 72 – 1
= 49 – 1
= 48
અને n2 + 1
= 72 + 1
= 49 + 1
= 50
આમ, માગેલી પાયથાગોરીઅન ત્રિપુટી 14, 48, 50 છે.
પ્રશ્ન (iii).
16
ઉત્તરઃ
અહીં 2n = 16
∴ n = 8
હવે, n2 – 1
= 82 – 1
= 64 – 1
= 63
અને n2 + 1
= 82 + 1
= 64 + 1
= 65
આમ, માગેલી પાયથાગોરીઅન ત્રિપુટી 16, 63, 65 છે.
![]()
પ્રશ્ન (iv).
18
ઉત્તરઃ
અહીં 2n = 18
∴ n = 9
હવે, n2 – 1
= 92 – 1
= 81 – 1
= 80
અને n2 + 1
= 92 + 1
= 81 + 1
= 82
આમ, માગેલી પાયથાગોરીઅન ત્રિપુટી 18, 80, 82 છે.