GSEB Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ InText Questions

Gujarat Board GSEB Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ InText Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ InText Questions

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબ 90)

નીચે આપેલ સંખ્યાઓ વચ્ચે આવતી પૂર્ણવર્ગ સંખ્યાઓ શોધોઃ

પ્રશ્ન (i).
30 અને 40
ઉત્તરઃ
જુઓ : 1 × 1 = 1
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16
5 × 5 = 25
6 × 6 = 36
7 × 7 = 49
આમ, 36 એ 30 અને 40 વચ્ચેની પૂર્ણવર્ગ સંખ્યા છે.

પ્રશ્ન (ii).
50 અને 60
ઉત્તરઃ
જુઓ : 7 × 7 = 49 અને 8 × 8 = 64
∴ 49 અને 64ની વચ્ચેની કોઈ પણ સંખ્યા પૂર્ણવર્ગ નથી.
∴ 50 અને 60 વચ્ચેની કોઈ પણ સંખ્યા પૂર્ણવર્ગ નથી.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 90-91)

1. નીચે આપેલી સંખ્યાઓ પૂર્ણવર્ગ સંખ્યાઓ છે? તમને કેવી રીતે ખબર પડી તે પણ જણાવો?
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 1069
(vi) 2061
એવી પાંચ સંખ્યાઓ જણાવો કે જેના એકમના અંક પરથી જ જાણી શકાય કે તે વર્ગ સંખ્યા નથી.
ઉત્તરઃ
(i) 1057
અહીં આપેલી સંખ્યા 1057નો એકમનો અંક 7 છે.
હવે, જે સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય, તે સંખ્યા જ પૂર્ણવર્ગ સંખ્યા હોઈ શકે.
∴ 1057 એ પૂર્ણવર્ગ સંખ્યા નથી.

(ii) 23453
અહીં આપેલી સંખ્યા 23453નો એકમનો અંક 3 છે.
હવે, જે સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય, તે સંખ્યા જ પૂર્ણવર્ગ સંખ્યા હોઈ શકે.
∴ 23453 એ પૂર્ણવર્ગ સંખ્યા નથી.

(iii) 7928
અહીં આપેલી સંખ્યા 7928નો એકમનો અંક 8 છે.
હવે, જે સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય, તે સંખ્યા જ પૂર્ણવર્ગ સંખ્યા હોઈ શકે.
∴ 7928 એ પૂર્ણવર્ગ સંખ્યા નથી.

(iv) 222222
અહીં આપેલી સંખ્યા 222222નો એકમનો અંક 2 છે.
હવે, જે સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય, તે સંખ્યા જ પૂર્ણવર્ગ સંખ્યા હોઈ શકે.
∴ 222222 એ પૂર્ણવર્ગ સંખ્યા નથી.

(v) 1069
અહીં આપેલી સંખ્યા 1069નો એકમનો અંક 9 છે.
હવે, જે સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય, તે સંખ્યા જ પૂર્ણવર્ગ સંખ્યા હોઈ શકે.
∴ 1069 સંખ્યા પૂર્ણવર્ગ સંખ્યા હોય કે ન પણ હોય.
હવે, 30 × 30 = 900, 31 × 11 = 961, 32 × 32 = 1024
અને 33 × 33 = 1089
એવી કોઈ પ્રાકૃતિક સંખ્યા 1024 અને 1089 વચ્ચેની નથી જે પૂર્ણવર્ગ હોય.
∴ 1069 એ પૂર્ણવર્ગ સંખ્યા નથી.

(vi) 2061
અહીં આપેલી સંખ્યા 2061નો એકમનો અંક 1 છે.
હવે, જે સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય, તે સંખ્યા જ પૂર્ણવર્ગ સંખ્યા હોઈ શકે.
∴ 2061 સંખ્યા પૂર્ણવર્ગ સંખ્યા હોય કે ન પણ હોય.
હવે, 45 × 45 = 2025 અને 46 × 46 = 2116
એવી કોઈ પ્રાકૃતિક સંખ્યા 2025 અને 2116 વચ્ચેની નથી જે પૂર્ણવર્ગ હોય.
∴ 2061 એ પૂર્ણવર્ગ સંખ્યા નથી.

2. એવી પાંચ સંખ્યાઓ જણાવો કે જેના એકમના અંક પરથી અનુમાન ન કરી શકાય કે તે વર્ગ સંખ્યા હશે કે નહિ હોય.
ઉત્તરઃ
આપણે એવી પાંચ સંખ્યાઓ લખીશું કે આ સંખ્યાનો એકમનો અંક 0, 1, 4, 5, 6 કે 9 હોય. આવી સંખ્યાઓ પૂર્ણવર્ગ સંખ્યા હોય કે ન પણ હોય.
પાંચ સંખ્યાઓ : 710, 2431, 524, 215, 326

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 91)

123², 77², 82², 161² અને 109²માં કઈ સંખ્યાનો એકમનો અંક 1 છે?
ઉત્તરઃ
અહીં 161 અને 109ના વર્ગનો એકમનો અંક 1 છે.
જે સંખ્યાના એકમનો અંક 1 અથવા 9 હોય તે જ સંખ્યાના વર્ગનો એકમનો અંક 1 હોય.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 91)

નીચેનામાંથી કઈ સંખ્યાનો એકમનો અંક 6 હશે?

પ્રશ્ન (i).
19²
ઉત્તરઃ
અહીં સંખ્યા 19નો એકમનો અંક 9 છે. (જુઓ: 9 × 9 = 81)
∴ 19²ના એકમનો અંક 6 ન હોય.

પ્રશ્ન (ii).
24²
ઉત્તરઃ
અહીં સંખ્યા 24નો એકમનો અંક 4 છે. (જુઓઃ 4 × 4 = 16)
∴ 24²ના એકમનો અંક 6 છે.

પ્રશ્ન (iii).
26²
ઉત્તરઃ
અહીં સંખ્યા 26નો એકમનો અંક 6 છે. (જુઓ : 6 × 6 = 36)
∴ 26²ના એકમનો અંક 6 છે.

પ્રશ્ન (iv).
36²
ઉત્તરઃ
અહીં સંખ્યા 36નો એકમનો અંક 6 છે. (જુઓ: 6 × 6 = 36)
∴ 36²ના એકમનો અંક 6 છે.

પ્રશ્ન (v).
34²
ઉત્તરઃ
અહીં સંખ્યા 34નો એકમનો અંક 4 છે. (જુઓઃ 4 × 4 = 16)
∴ 34²ના એકમનો અંક 6 છે.
આમ, 24, 26, 34 અને 36ના વર્ગનો એકમનો અંક 6 છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 92)

નીચે આપેલી સંખ્યાનો વર્ગ કરવાથી મળતી સંખ્યાનો એકમનો અંક શું મળશે?

પ્રશ્ન (i).
1234
ઉત્તરઃ
1234નો એકમનો અંક 4 છે અને 4 × 4 = 16
∴ (1234)² સંખ્યાનો એકમનો અંક 6 હોય.

પ્રશ્ન (ii).
26387
ઉત્તરઃ
26387નો એકમનો અંક 7 છે અને 7 × 7 = 49
∴ (26387)² સંખ્યાનો એકમનો અંક 9 હોય.

પ્રશ્ન (iii).
52698
ઉત્તરઃ
52698નો એકમનો અંક 8 છે અને 8 × 8 = 64
∴ (52698)² સંખ્યાનો એકમનો અંક 4 હોય.

પ્રશ્ન (iv).
99880
ઉત્તરઃ
99880નો એકમનો અંક 0 છે અને 0 × 0 = 0
∴ (99880)² સંખ્યાનો એકમનો અંક 1 હોય.

પ્રશ્ન (v).
21222
ઉત્તરઃ
21222નો એકમનો અંક 2 છે અને 2 × 2 = 4
∴ (21222)² સંખ્યાનો એકમનો અંક 4 હોય.

પ્રશ્ન (vi).
9106
ઉત્તરઃ
9106નો એકમનો અંક 6 છે અને 6 × 6 = 36
∴ (9106)² સંખ્યાનો એકમનો અંક 6 હોય.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 92)

1. નીચે આપેલી કઈ સંખ્યાઓનો વર્ગ કરવાથી તે એકી સંખ્યા કે બેકી સંખ્યા આવશે? કેમ?

પ્રશ્ન (i).
727
ઉત્તરઃ
727નો એકમનો અંક 7 છે. તેથી તે એકી સંખ્યા છે.
એકી સંખ્યાનો વર્ગ એકી સંખ્યા હોય. તેથી 727નો વર્ગ એકી સંખ્યા છે.

પ્રશ્ન (ii).
158
ઉત્તરઃ
158નો એકમનો અંક 8 છે. તેથી તે બેકી સંખ્યા છે.
બેકી સંખ્યાનો વર્ગ બેકી સંખ્યા હોય. તેથી 158નો વર્ગ બેકી સંખ્યા છે.

પ્રશ્ન (iii).
269
ઉત્તરઃ
269નો એકમનો અંક 9 છે. તેથી તે એકી સંખ્યા છે.
એકી સંખ્યાનો વર્ગ એકી સંખ્યા હોય. તેથી 269નો વર્ગ એકી સંખ્યા છે.

પ્રશ્ન (iv).
1980
ઉત્તરઃ
1980નો એકમનો અંક 0 છે. તેથી તે બેકી સંખ્યા છે.
બેકી સંખ્યાનો વર્ગ બેકી સંખ્યા હોય. તેથી 1980નો વર્ગ બેકી સંખ્યા છે.

2. નીચે આપેલી સંખ્યાઓનો વર્ગ કરવાથી મળતી સંખ્યામાં કેટલાં શૂન્યો હશે?

પ્રશ્ન (i).
60
ઉત્તરઃ
60માં શૂન્યની સંખ્યા 1 છે.
∴ 60²માં શૂન્યની સંખ્યા 2 હોય. (∵ 60² = 3600)

પ્રશ્ન (ii).
400
ઉત્તરઃ
400માં શૂન્યની સંખ્યા 2 છે.
∴ 400²માં શૂન્યની સંખ્યા 4 હોય. (∵400² = 160000)

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 94)

પ્રશ્ન 1.
9² અને 10² વચ્ચે કેટલી પ્રાકૃતિક સંખ્યાઓ આવે? તેમજ 11² અને 12² વચ્ચે કેટલી?
ઉત્તરઃ
બે ક્રમિક સંખ્યાઓ n² અને (n + 1)² વચ્ચેની પૂર્ણવર્ગ ન હોય તેવી પ્રાકૃતિક સંખ્યાઓ 2n મળે.
(a) 9² અને 10² વચ્ચે:
અહીં n = 9 અને n + 1 = 10
∴ 9² અને 10² વચ્ચેની પ્રાકૃતિક સંખ્યાઓ = 2 × n = 2 × 9 = 18
ચેક: 81 અને 100 વચ્ચે કુલ 18 પ્રાકૃતિક સંખ્યાઓ છે.

(b) 11² અને 12² વચ્ચે :
અહીં n = 11 અને n + 1 = 12
∴ 11² અને 12² વચ્ચેની પ્રાકૃતિક સંખ્યાઓ = 2 × n
= 2 × 11
= 22
ચેક : 121 અને 144 વચ્ચે કુલ 22 પ્રાકૃતિક સંખ્યાઓ છે.

પ્રશ્ન 2.
નીચે આપેલ પૂર્ણવર્ગ સંખ્યાઓની જોડીઓ વચ્ચે પૂર્ણવર્ગ ન હોય તેવી કેટલી સંખ્યાઓ આવે?

પ્રશ્ન (i).
100² અને 101²
ઉત્તરઃ
100² અને 101² વચ્ચે:
અહીં n = 100 અને n + 1 = 101
100² અને 101² વચ્ચેની પ્રાકૃતિક સંખ્યાઓ = 2 × n
= 2 × 100
= 200
100 અને 101 બે ક્રમિક પ્રાકૃતિક સંખ્યાઓ છે.
∴ 100² અને 101² વચ્ચે પૂર્ણવર્ગ ન હોય તેવી 200 સંખ્યાઓ છે.

પ્રશ્ન (ii).
90² અને 91²
ઉત્તરઃ
90 અને 91 વચ્ચે :
અહીં n = 90 અને n + 1 = 91
90² અને 91² વચ્ચેની પ્રાકૃતિક સંખ્યાઓ = 2 × n
= 2 × 90
= 180
90 અને 91 બે ક્રમિક પ્રાકૃતિક સંખ્યાઓ છે.
∴ 90² અને 91² વચ્ચે પૂર્ણવર્ગ ન હોય તેવી 180 સંખ્યાઓ છે.

પ્રશ્ન (iii).
1000² અને 1001²
ઉત્તરઃ
1000² અને 1001² વચ્ચે :
અહીં n = 1000 અને n + 1 = 1001
1000² અને 1001² વચ્ચેની પ્રાકૃતિક સંખ્યાઓ = 2 × n
= 2 × 1000
= 2000
1000 અને 1001 બે ક્રમિક પ્રાકૃતિક સંખ્યાઓ છે.
∴ 1000² અને 1001² વચ્ચે પૂર્ણવર્ગ ન હોય તેવી 2000 સંખ્યાઓ છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 94)

નીચેની સંખ્યા પૂર્ણવર્ગ સંખ્યા છે કે નહિ તે કહોઃ
[નોંધઃ ધ્યાનમાં રાખો કે જે પ્રાકૃતિક સંખ્યાને 1થી શરૂ કરી ક્રમિક એકી સંખ્યાઓના સરવાળા રૂપે દર્શાવી શકાય તે પ્રાકૃતિક સંખ્યા પૂર્ણવર્ગ હોય.]

પ્રશ્ન (i).
121
ઉત્તરઃ
121 – 1 = 120
120 – 3 = 117
117 – 5 = 112
112 – 7 = 105
105 – 9 = 96
96 – 11 = 85
85 – 13 = 72
72 – 15 = 57
57 – 17 = 40
40 – 19 = 21
21 – 21 = 0
જુઓ : 121 = 1 + 3 + 5 + 7 + 9 + 10 + 13 + 15 + 17 + 19 + 21
આમ, 121 એ પૂર્ણવર્ગ સંખ્યા છે.

પ્રશ્ન (ii).
55
ઉત્તરઃ
55 – 1 = 54
54 – 3 = 51
51 – 5 = 46
46 – 7 = 39
39 – 9 = 30
30 – 11 = 19
19 – 13 = 6
6 – 15 = – 9
55ને 1થી શરૂ થતા ક્રમિક એકી સંખ્યાઓના સરવાળા રૂપે લખી શકાતું નથી.
∴ 55 એ પૂર્ણવર્ગ સંખ્યા નથી.

પ્રશ્ન (iii).
81
ઉત્તરઃ
81 – 1 = 80
80 – 3 = 77
77 – 5 = 72
72 – 7 = 65
65 – 9 = 56
56 – 11 = 45
45 – 13 = 32
32 – 15 = 17
17 – 17 = 0
∴ 81 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17
આમ, 81 એ પૂર્ણવર્ગ સંખ્યા છે.

પ્રશ્ન (iv).
49
ઉત્તરઃ
49 – 1 = 48
48 – 3 = 45
45 – 5 = 40
40 – 7 = 33
33 – 9 = 24,
24 – 11 = 13
13 – 13 = 0
∴ 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13
આમ, 49 એ પૂર્ણવર્ગ સંખ્યા છે.

પ્રશ્ન (v).
69
ઉત્તરઃ
69 – 1 = 68
68 – 3 = 65
65 – 5 = 60
60 – 7 = 53
53 – 9 = 44
44 – 11 = 33
33 – 13 = 20
20 – 15 = 5
5 – 17 = – 12
69ને 1થી શરૂ થતા ક્રમિક એકી સંખ્યાઓના સરવાળા રૂપે લખી શકાતું નથી.
∴ 69 એ પૂર્ણવર્ગ સંખ્યા નથી.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 95)

1. નીચેની સંખ્યાઓને બે ક્રમિક સંખ્યાના સરવાળા તરીકે રજૂ કરો:
જાણો : n² = \(\frac{n^{2}-1}{2}+\frac{n^{2}+1}{2} \)

(i) 21²
ઉત્તરઃ
21²
n = 21

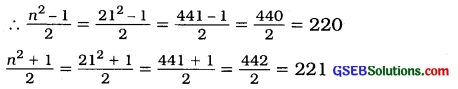
∴ 21² = 220 + 221 = 441

(ii) 13²
ઉત્તરઃ
13²
n = 13

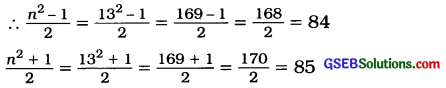
∴ 13² = 84 + 85 = 169

(iii) 11²
ઉત્તરઃ
11²
n = 11

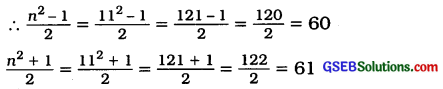
∴ 11² = 60 + 61 = 121

(iv) 19²
ઉત્તરઃ
19²
n = 19

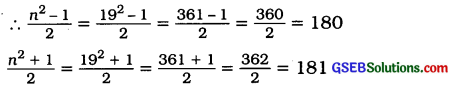
∴ 19² = 180 + 181 = 361

2. શું એ પણ સાચું છે કે, બે ક્રમિક સંખ્યાઓનો સરવાળો એ કોઈ સંખ્યાનો વર્ગ હશે? તમારા જવાબના આધાર માટે ઉદાહરણ પણ આપો.
ઉત્તરઃ
ના, આ હંમેશ સત્ય નથી.
(i) 3 + 4 = 7, જુઓ 7 એ પૂર્ણવર્ગ સંખ્યા નથી.
(ii) 10 + 11 = 21, જુઓ 21 એ પૂર્ણવર્ગ સંખ્યા નથી.

પરંતુઃ
(i) 4 + 5 = 9, જુઓ 9 એ પૂર્ણવર્ગ સંખ્યા છે.
(ii) 12 + 18 = 25, જુઓ 25 એ પૂર્ણવર્ગ સંખ્યા છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 95)

નીચેની સંખ્યા માટે પાઠ્યપુસ્તકમાં આપેલ તરાહ મુજબ વર્ગ કરોઃ
(i) 111111²
(ii) 1111111²
ઉત્તરઃ
પાઠ્યપુસ્તકમાં આપેલી તરાહનો ઉપયોગ કરતાં –
(i) (111111)² = 12345654321
(ii) (1111111)² = 1234567654321

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 95)

શું તમે પાઠ્યપુસ્તકમાં આપેલી તરાહની મદદથી આપેલી સંખ્યાઓનો વર્ગ શોધી શકો?
(i) 6666667²
(ii) 66666667²
ઉત્તરઃ
(i) હા, 6666667² = 44444448888889
(ii) હા, 66666667² = 4444444488888889

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 97)

નીચે આપેલી સંખ્યામાં એકમનો અંક 5 છે, તેમનો વર્ગ શોધોઃ
[નોંધઃ જેનો એકમનો અંક 5 છે તેવી સંખ્યાનો વર્ગ = a (a + 1) × 100 + 25 જ્યાં, a = દશકનો અંક]

પ્રશ્ન (i).
15
ઉત્તરઃ
(15)² = 1 × (1 + 1) × 100 + 25
= 1 × 2 × 100 + 25
= 200 + 25
= 225
જાણોઃ

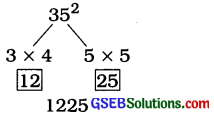
પ્રશ્ન (ii).
95
ઉત્તરઃ
(95)² = 9 (9 + 1) × 100 + 25
= 9 × 10 × 100 + 25
= 9000 + 25
= 9025

પ્રશ્ન (iii).
105
ઉત્તરઃ
(105)² = 10 × (10 + 1) × 100 + 25
= 10 × 11 × 100 + 25
= 11000 + 25
= 11025
જાણો:

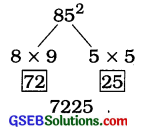
પ્રશ્ન (iv).
205
ઉત્તરઃ
(205)² = 20 × (20 + 1) × 100 + 25
= 20 × 21 × 100 + 25
= 42000 + 25
= 42025

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 99)

પ્રશ્ન (i).
જો 11² = 121, તો 121નું વર્ગમૂળ?
ઉત્તરઃ
121નું વર્ગમૂળ 11 છે.

પ્રશ્ન (ii).
જો 14² = 196, તો 196નું વર્ગમૂળ?
ઉત્તરઃ
196નું વર્ગમૂળ 14 છે.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 99)

(i) (-1)² = 1, શું -1 એ 1નું વર્ગમૂળ છે?
(ii) (-2)² = 4, શું -2 એ 4નું વર્ગમૂળ છે?
(iii) (-9)² = 81, શું -9 એ 81નું વર્ગમૂળ છે?
ઉત્તરઃ
પૂર્ણવર્ગ સંખ્યાનું વર્ગમૂળ ધન અને ત્રણ બંને સંખ્યા મળે.
દા. ત., \(\sqrt{9}\) = + 3 અથવા -3
(i) (-1) × (-1) = 1 એટલે કે (-1)² = 1
∴ 1નું વર્ગમૂળ (-1) હોઈ શકે.

(ii) (-2) × (-2) = 4 એટલે કે (-2)² = 4
∴ 4નું વર્ગમૂળ (-2) હોઈ શકે.

(iii) (-9) × (-9) = 81 એટલે કે (-9)² = 81
∴ 81નું વર્ગમૂળ (-9) હોઈ શકે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 100)

1થી શરૂ કરી ક્રમિક અયુગ્મ સંખ્યાની પુનરાવર્તિત બાદબાકી કરીને જણાવો કે નીચેની સંખ્યાઓ પૂર્ણવર્ગ છે કે નહીં? જો પૂર્ણવર્ગ હોય, તો તેમનું વર્ગમૂળ શોધોઃ

(i) 121
ઉત્તરઃ
121ને 1થી શરૂ થતા ક્રમિક અયુગ્મ સંખ્યાઓની બાદબાકી રૂપે લખીએ :
121 – 1 = 120
120 – 3 = 117
117 – 5 = 112
112 – 7 = 105
105 – 9 = 96
96 – 11 = 85
85 – 13 = 72
72 – 15 = 57
57 – 17 = 40
40 – 19 = 21
21 – 21 = 0
∴ \(\sqrt{121}\) = 11
∴ 121 એ પૂર્ણવર્ગ સંખ્યા છે.

(ii) 55
ઉત્તરઃ
∵ 55 – 1 = 54
54 – 3 = 51
51 – 5 = 46
46 – 7 = 39
39 – 9 = 30
30 – 11 = 19
19 – 13 = 6
6 – 15 = – 9
55ને 1થી શરૂ થતા ક્રમિક અયુગ્મ સંખ્યાઓની બાદબાકી રૂપે લખી શકાતું નથી.
∴ 55 એ પૂર્ણવર્ગ સંખ્યા નથી.

(iii) 36
ઉત્તરઃ
∵ 36 – 1 = 35
35 – 3 = 32
32 – 5 = 27
27 – 7 = 20
20 – 9 = 11
11 – 11 = 0
∴ \(\sqrt{36}\) = 6
∴ 36 એ પૂર્ણવર્ગ સંખ્યા છે.

(iv) 49
ઉત્તરઃ
49 – 1 = 48
48 – 3 = 45
45 – 5 = 40
40 – 7 = 33
33 – 9 = 24
24 – 11 = 13
13 – 13 = 0
∴ \(\sqrt{49}\) = 7
∴ 49 એ પૂર્ણવર્ગ સંખ્યા છે.

(v) 90
ઉત્તરઃ
90 – 1 = 89
89 – 3 = 86
86 – 5 = 81
81 – 7 = 74
74 – 9 = 65
65 – 11 = 54
54 – 13 = 41
41 – 15 = 26
26 – 17 = 9
9 – 19 = – 10
90ને 1થી શરૂ થતા ક્રમિક અયુગ્મ સંખ્યાઓના સરવાળા રૂપે લખી શકાતું નથી.
∴ 90 એ પૂર્ણવર્ગ સંખ્યા નથી.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 103)

શું આપણે એમ કહી શકીએ કે, n અંકોવાળી પૂર્ણવર્ગ સંખ્યાના વર્ગમૂળની સંખ્યા જો n બેઠી હોય, તો \(\frac{n}{2}\) મળે અને એકી હોય, તો \(\frac{(n+1)}{2}\) મળે?
ઉત્તરઃ
હા, એ સાચું છે કે n અંકોવાળી પૂર્ણવર્ગ સંખ્યાના વર્ગમૂળની સંખ્યા જો n બેકી હોય, n તો \(\frac{n}{2}\) મળે અને એકી હોય, તો \(\frac{(n+1)}{2}\) મળે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 105)

નીચે આપેલી સંખ્યાઓનું વર્ગમૂળ શોધ્યા વિના જણાવો કે, મળતા વર્ગમૂળના અંકોની સંખ્યા કેટલી હશે?

પ્રશ્ન (i).
25600
ઉત્તરઃ
25600
25600માં અંકોની સંખ્યા = 5
∴ n = 5 જે એકી સંખ્યા છે.
∴ 25600ના વર્ગમૂળની સંખ્યાના અંકોની સંખ્યા = \(\frac{n+1}{2}\)
= \(\frac{5+1}{2}\)
= \(\frac {6}{2}\)
= 3

પ્રશ્ન (ii).
100000000
ઉત્તરઃ
100000000
100000000માં અંકોની સંખ્યા = 9
∴ n = 9 જે એકી સંખ્યા છે.
∴ 100000000ના વર્ગમૂળની સંખ્યાના અંકોની સંખ્યા = \(\frac{n+1}{2}\)
= \(\frac{9+1}{2}\)
= \(\frac {10}{2}\)
= 5

પ્રશ્ન (iii).
38864
ઉત્તરઃ
36864
36864માં અંકોની સંખ્યા = 5
∴ n = 5 જે એકી સંખ્યા છે.
∴ 36864ના વર્ગમૂળની સંખ્યાના અંકોની સંખ્યા = \(\frac{n+1}{2}\)
= \(\frac{5+1}{2}\)
= \(\frac {6}{2}\)
= 3

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 107)

નીચેની સંખ્યાઓના વર્ગમૂળની સૌથી નજીકની પૂર્ણ સંખ્યા તરીકે શું મળે તેની ગણતરી કરોઃ

પ્રશ્ન (i).
\(\sqrt{80}\)
ઉત્તરઃ
\(\sqrt{80}\)
∴ 10² = 100, 9² = 81, 8² = 64
∴ 80 એ 64 અને 81ની વચ્ચે છે.
∴ 64 < 80 < 81
∴ 8² < 80 < 9²
∴ 8 < 80 < 9
આમ, \(\sqrt{80}\) એ 8 અને 9ની વચ્ચે છે. \(\sqrt{80}\) ની નજીકની પૂર્ણ સંખ્યા 9 છે.

પ્રશ્ન (ii).
\(\sqrt{1000}\)
ઉત્તરઃ
\(\sqrt{1000}\)
∴ 30² = 900, 31² = 961, 32² = 1024
∴ 1000 એ 961 અને 1024ની વચ્ચે છે.
∴ 961 < 1000 < 1024
∴ 31² < 1000 < 32²
∴ 31 < \(\sqrt{1000}\) < 32
આમ, \(\sqrt{1000}\) એ 31 અને 32ની વચ્ચે છે. \(\sqrt{1000}\) ની નજીકની પૂર્ણ સંખ્યા 32 છે.

પ્રશ્ન (iii).
\(\sqrt{350}\)
ઉત્તરઃ
\(\sqrt{350}\)
∴ 18² = 324 અને 19² = 361
∴ 350 એ 324 અને 361ની વચ્ચે છે.
∴ 324 < 350 < 361
∴ 18² < 350 < 19²
∴ 18 < \(\sqrt{350}\) < 19
આમ, \(\sqrt{350}\) એ 18 અને 19ની વચ્ચે છે. \(\sqrt{350}\) ની નજીકની પૂર્ણ સંખ્યા 19 છે.

પ્રશ્ન (iv).
\(\sqrt{500}\)
ઉત્તરઃ
\(\sqrt{500}\)
∴ 22² = 484 અને 23² = 529
∴ 500 એ 484 અને 529ની વચ્ચે છે.
∴ 484 < 500 < 529
∴ 22² < 500 < 23²
∴ 22 < \(\sqrt{500}\) < 23
આમ, \(\sqrt{500}\) એ 22 અને 23ની વચ્ચે છે. \(\sqrt{500}\) ની નજીકની પૂર્ણ સંખ્યા 22 છે.